インターネットサービスやログ解析では、日々膨大なデータが生成されます。
ユーザー数やアクセス元IPアドレス数などを数えるだけでも、データ量が増えるほど処理は重くなります。
そのような中で注目されるのが、厳密な数ではなく「およその数」を、圧倒的に小さいメモリで素早く数える確率的アルゴリズムです。
本記事では、その代表格であるHyperLogLog(ハイパーログログ)について、仕組みと特徴をわかりやすく解説します。
HyperLogLogとは何か
HyperLogLog(HLL)は、巨大なデータ集合の中に「異なる値が何種類あるか」を、およその値で推定するための確率的アルゴリズムです。
ここでいう「数える対象」は、ユーザーID、IPアドレス、検索クエリ、商品IDなど何でもかまいません。
通常、異なる要素の数(基数・カーディナリティ)を数えるには、すべての要素を保存して重複を排除する必要があります。
しかし、データが億単位・兆単位になるとメモリも計算時間も現実的ではありません。
そこで登場するのがHyperLogLogです。
HLLは「わずかなメモリで、かなり精度の高い推定を行う」ことを目指したアルゴリズムです。
どのような場面で使われるか
HyperLogLogは、次のようなユースケースでよく使われます。
- 日次・月次のユニークユーザー数(UU)の計測
- 広告配信でのユニークインプレッション数
- ログ解析でのユニークIPアドレスやユニークURLのカウント
- 分散システムにおける巨大なイベントストリームの重複なし件数の推定
多くのデータストアや分析基盤(例: RedisのPFADD / PFCOUNT、BigQueryのHLL系関数など)にHyperLogLogが組み込まれており、実運用でも広く利用されています。
HyperLogLogの特徴
メモリ消費が極端に小さい
HyperLogLogの最大の特徴は、必要なメモリ量が要素数にほとんど依存しない点です。
たとえば、標準的な設定では数百万〜数億のユニーク要素を数えるのに、わずか数キロバイト程度しか必要としません。
一方、厳密カウントであれば、ユニーク要素数に比例してメモリが増えていきます。
1億ユーザー分のIDを保持しようとすれば、ギガバイト単位のメモリが必要になってもおかしくありません。
許容可能な誤差とトレードオフ
HyperLogLogは確率的アルゴリズムであるため、結果はあくまで近似値です。
典型的な設定では、誤差率がおよそ1〜2%程度に収まるように設計されています。
この誤差率は、レジスタ数(後述)を増やすことで小さくできますが、その分だけメモリは増えます。
ビジネスの現場では、たとえば「ユニークユーザー数が100万か102万か」という差は、意思決定にほとんど影響しない場合が多くあります。
そのような環境では、厳密さよりもメモリと速度を優先するHyperLogLogのメリットが際立ちます。
合成(マージ)が簡単
分散システムでは、複数のサーバーで別々にカウントした結果を後から合算したくなる場面が頻繁にあります。
HyperLogLogは2つのHLLを簡単にマージできる点も非常に重要です。
マージの操作はシンプルで、対応するレジスタごとに最大値を取るだけです。
これにより、次のような使い方ができます。
- サーバーA・B・CそれぞれでユニークユーザーをHLLで計測
- 後から3つのHLLをマージして、全体のユニークユーザー数を推定
この「マージのしやすさ」は、大規模分散処理(ストリーム処理やバッチ処理)との相性が非常に良い性質です。
基本アイデアを直感的に理解する
HyperLogLogの中身は数学的には少し複雑ですが、「ハッシュ値の中で、先頭にどれだけ連続した0が並ぶか」を統計的に利用するというのが根本のアイデアです。
直感的なたとえ話
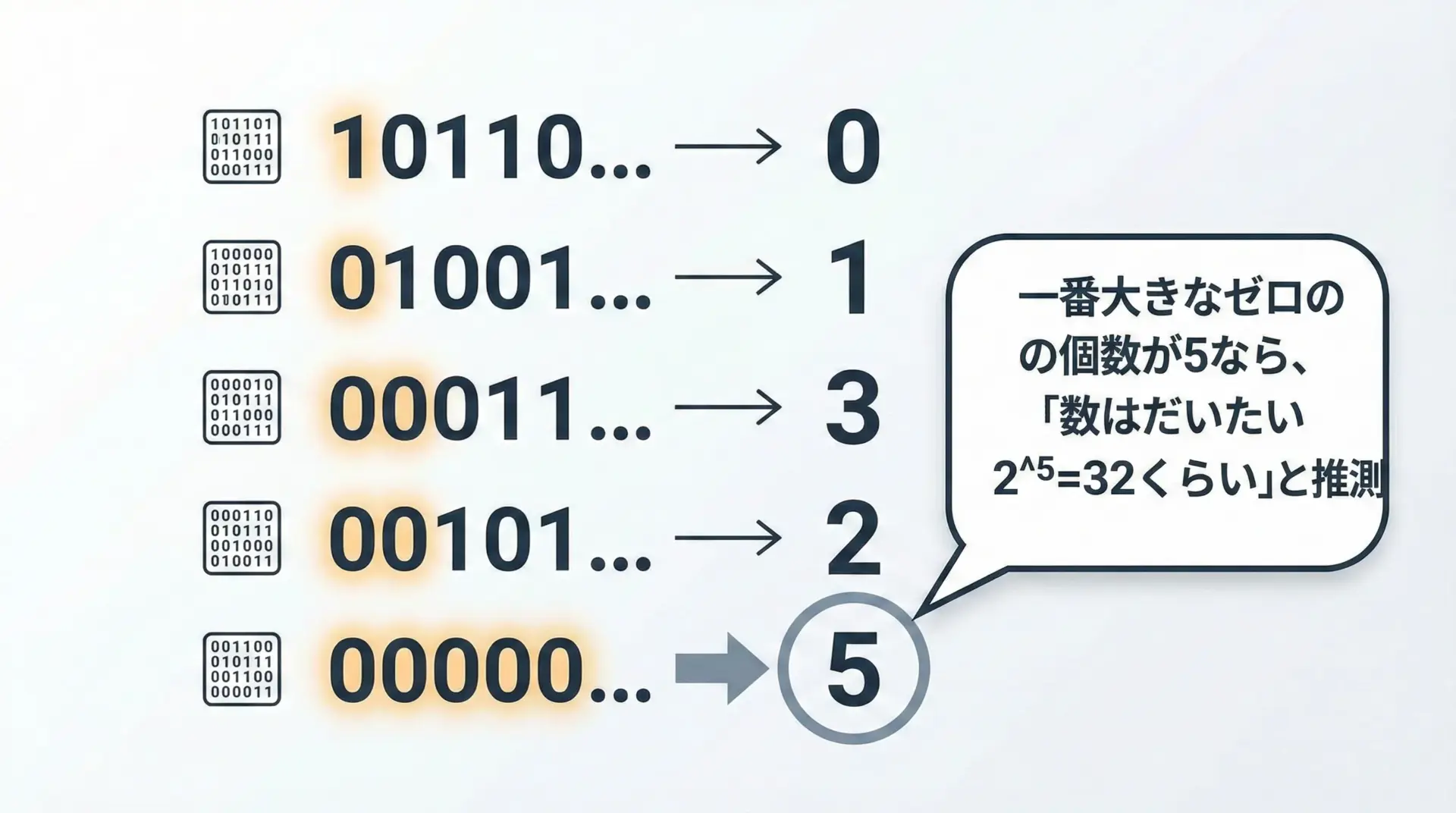
この図のように、ランダムなビット列がたくさんあるとき、先頭に長い0が出現する確率から、全体の個数を逆算することができます。
たとえば、32個ぐらいビット列があると、先頭に0が5個連続するような列が「そろそろ出てきてもおかしくない」程度の確率になります。
これを一般化すると、最大のゼロ連続長をRとすると、要素数はおおよそ2^Rぐらいと推定できます。
HyperLogLogは、このアイデアをより洗練させ、バラツキを減らして高精度にしたアルゴリズムです。
HyperLogLogの仕組み
ここからは、HyperLogLogの動作の流れを、概念レベルで整理してみます。
ステップ1: ハッシュ関数で値をビット列に変換する
まず、数えたい要素(ユーザーIDやIPアドレスなど)をハッシュ関数に通し、ランダムに見える長いビット列を得ます。
ハッシュ関数には、例えば64ビットのハッシュなどが使われます。
ここで重要なのは「値の分布ができるだけ一様になるようなハッシュ」を使うことです。
分布が偏ってしまうと、統計的な推定が歪んでしまうためです。
ステップ2: 先頭のビットで「どのレジスタを使うか」を決める
HyperLogLogは、多数のレジスタ(小さなカウンタ)の配列を内部に持っています。
これらの個数をmとし、そのインデックスを0〜m-1で表します。
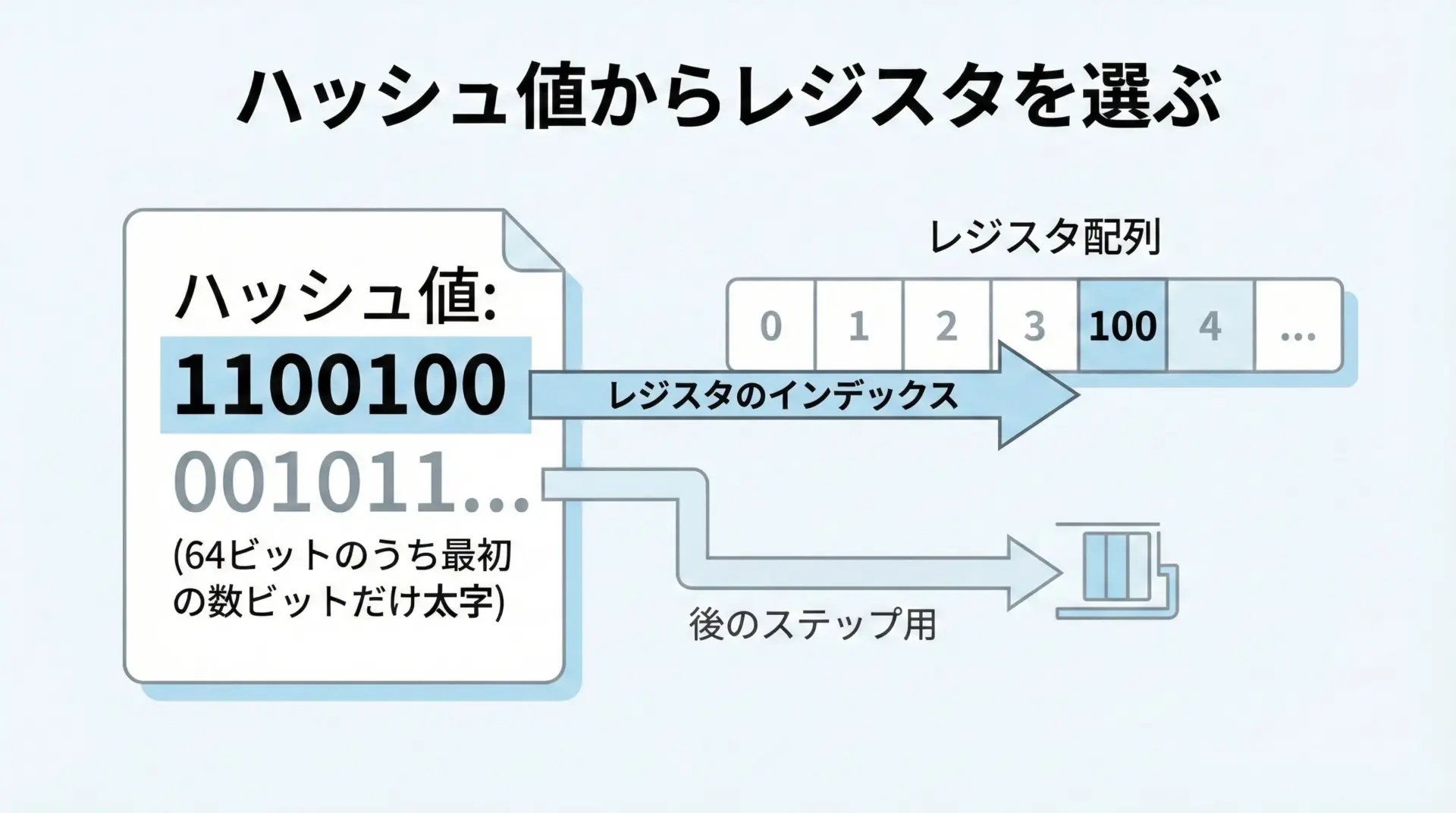
ハッシュ値の上位の数ビット(例えば最初の10ビット)を取り出し、それを2進数→整数として解釈すると0〜1023までの番号が得られます。
これを「どのレジスタを更新するかを決めるインデックス」として使います。
このインデックス決定により、要素はランダムに各レジスタへ振り分けられます。
レジスタ数が多いほど、全体をより細かく分割して観測できるイメージです。
ステップ3: 残りのビットで0の連続数を数える
インデックスとして使った上位ビットを取り除き、残りの下位ビット列について、先頭から何個の0が連続しているかを数えます。
これをrhoとします。
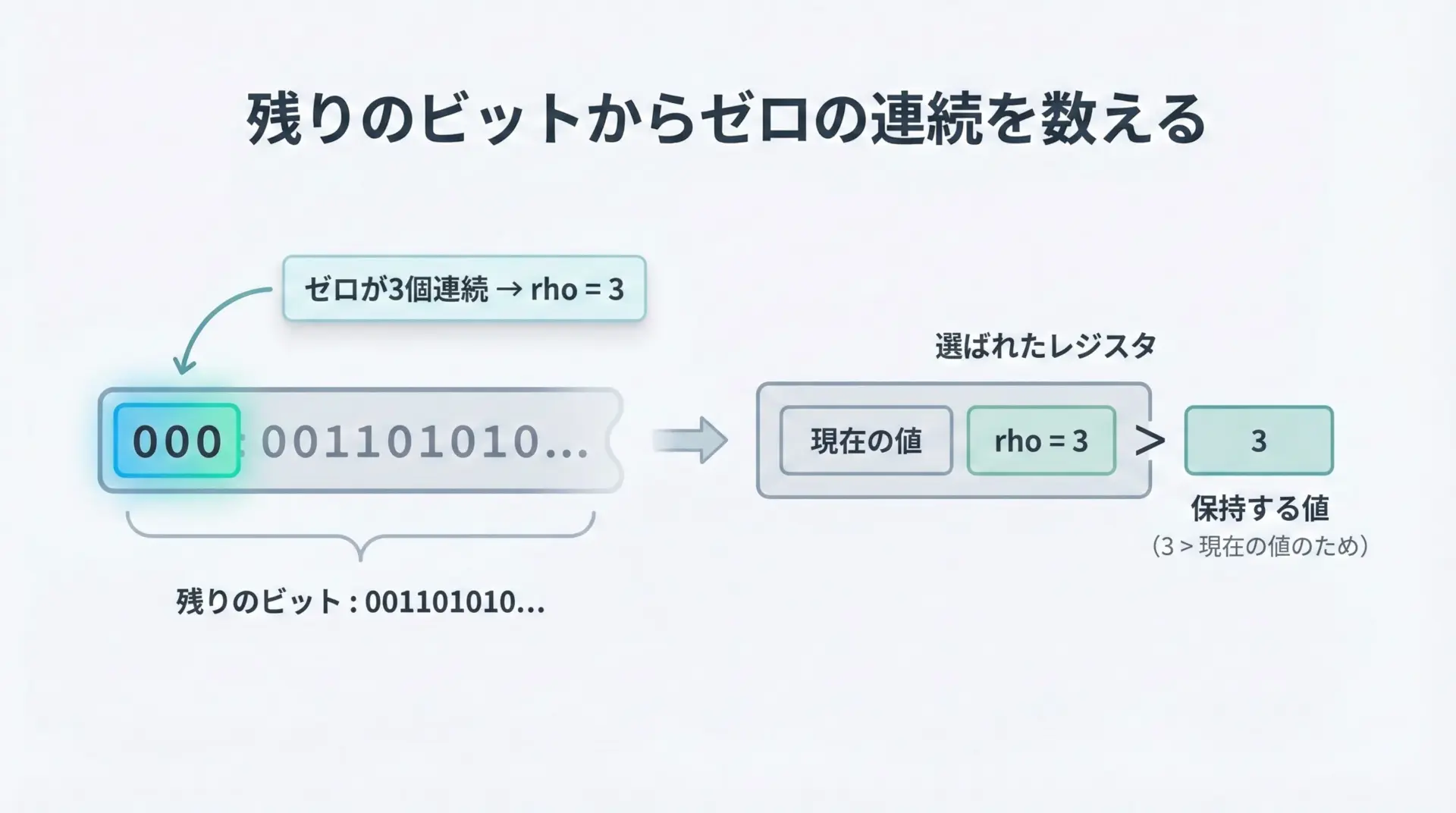
そして、そのレジスタに対し、
- すでに入っている値と
rhoを比較する - より大きい方の値でレジスタを更新する
という操作を行います。
これを、ストリームに流れてくる全ての要素について繰り返します。
ステップ4: レジスタ全体から基数を推定する
すべてのデータを処理し終えた段階で、各レジスタには「そのレジスタに振り分けられた要素の中で観測された最大のゼロ連続長」が記録されています。
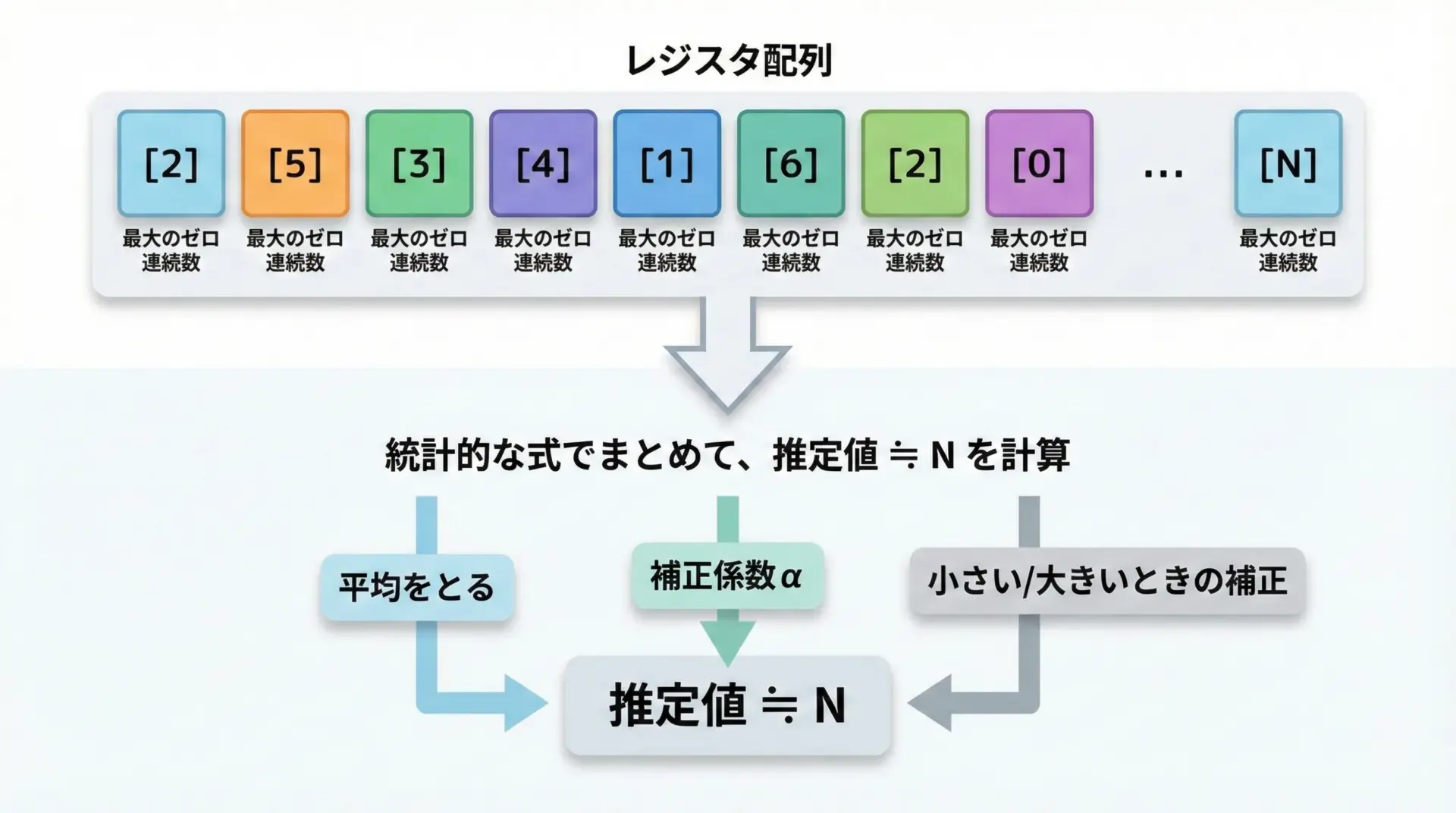
HyperLogLogでは、このレジスタ値の分布を統計的に処理し、次のようなイメージの式で全体の要素数を推定します。
- レジスタ値を2の冪に変換して平均を取る
- 経験的に導かれた定数
αでスケーリングする - 要素数が非常に少ない場合や、非常に多い場合のバイアス補正を行う
実際の公式は少し複雑ですが、考え方としては「各レジスタが観測したゼロ連続長から、そのレジスタに割り当てられた要素数を推定し、それらを合成して全体の要素数を推定する」と捉えると理解しやすくなります。
精度とパラメータ
HyperLogLogの挙動を理解するうえで重要になるのが、レジスタ数mと、それを決めるp(インデックスに使うビット数)の関係です。
レジスタ数と誤差の関係
レジスタ数mは通常2の冪で、m = 2^pと表されます。
一般に、推定値の相対誤差はおおよそ1 / √mに比例して小さくなることが知られています。
単純化したイメージとしては、次のように考えられます。
m = 2^10 = 1024レジスタ → 誤差は数パーセント程度mを4倍にすると誤差はおおよそ半分になる
一方で、メモリ消費はレジスタ数に比例して増えます。
したがって、「どれくらいの誤差を許容するか」と「どれくらいメモリを使えるか」のバランスを取ることが設計上のポイントになります。
メモリ使用量のイメージ
実装によって異なりますが、1つのレジスタは数ビット〜1バイト程度に収まるように設計されることが多いです。
例えば、m = 16384レジスタを1バイトずつ確保しても、必要なメモリはたったの16KBです。
それでいて、数億規模のユニーク数をそこそこの精度で推定できます。
数十KBのメモリで、ビッグデータ規模のユニークカウントができるというのは、従来の厳密カウントからすると非常にインパクトの大きな特徴です。
HyperLogLogの長所と短所
長所
HyperLogLogには、大きく次のようなメリットがあります。
1つ目はメモリ効率の圧倒的な良さです。
要素数が増えてもメモリ使用量がほぼ増えないため、長期間にわたる計測や大規模サービスでの利用に向いています。
2つ目は計算の軽さとストリーム処理への適合性です。
要素を1つ処理するごとの計算は「ハッシュ化」「インデックス計算」「ゼロ連続のカウント」「レジスタの最大値更新」といった局所的な操作だけで済みます。
これは、リアルタイムストリーム処理やオンライン集計に非常に適しています。
3つ目がマージのしやすさです。
レジスタごとの最大値を取るだけで複数のHLLを統合できるため、分散処理フレームワークやマイクロサービス間での集計にも組み込みやすくなっています。
短所と注意点
一方で、HyperLogLogには明確な制約もあります。
まず結果が近似値であることです。
常に数パーセント程度の誤差が存在するため、「1件単位で正確でなければならない用途」には向きません。
たとえば、請求金額を決定する課金ロジックなどには厳密カウントを使うべきでしょう。
次に、ある時点でのHLLから「個々の要素」を取り出すことはできないという点です。
HyperLogLogは要素をまとめて統計量に変換してしまうため、後から「どのユーザーIDが含まれていたか」を知ることはできません。
また、小さなカウントに対しては誤差の相対的な影響が大きくなることも注意が必要です。
たとえば、ユニーク数が100前後しかないのに2〜3程度の誤差が出ると、それは2〜3%ではなくもっと大きな割合になります。
このようなケースでは、HyperLogLogよりも単純なビットマップや小さなハッシュセットの方が適している場合もあります。
実システムでの使われ方の例
ここでは、現代のシステムでHyperLogLogがどのように使われているかの典型例をいくつか紹介します。
分散Webサービスでのユニークユーザー計測
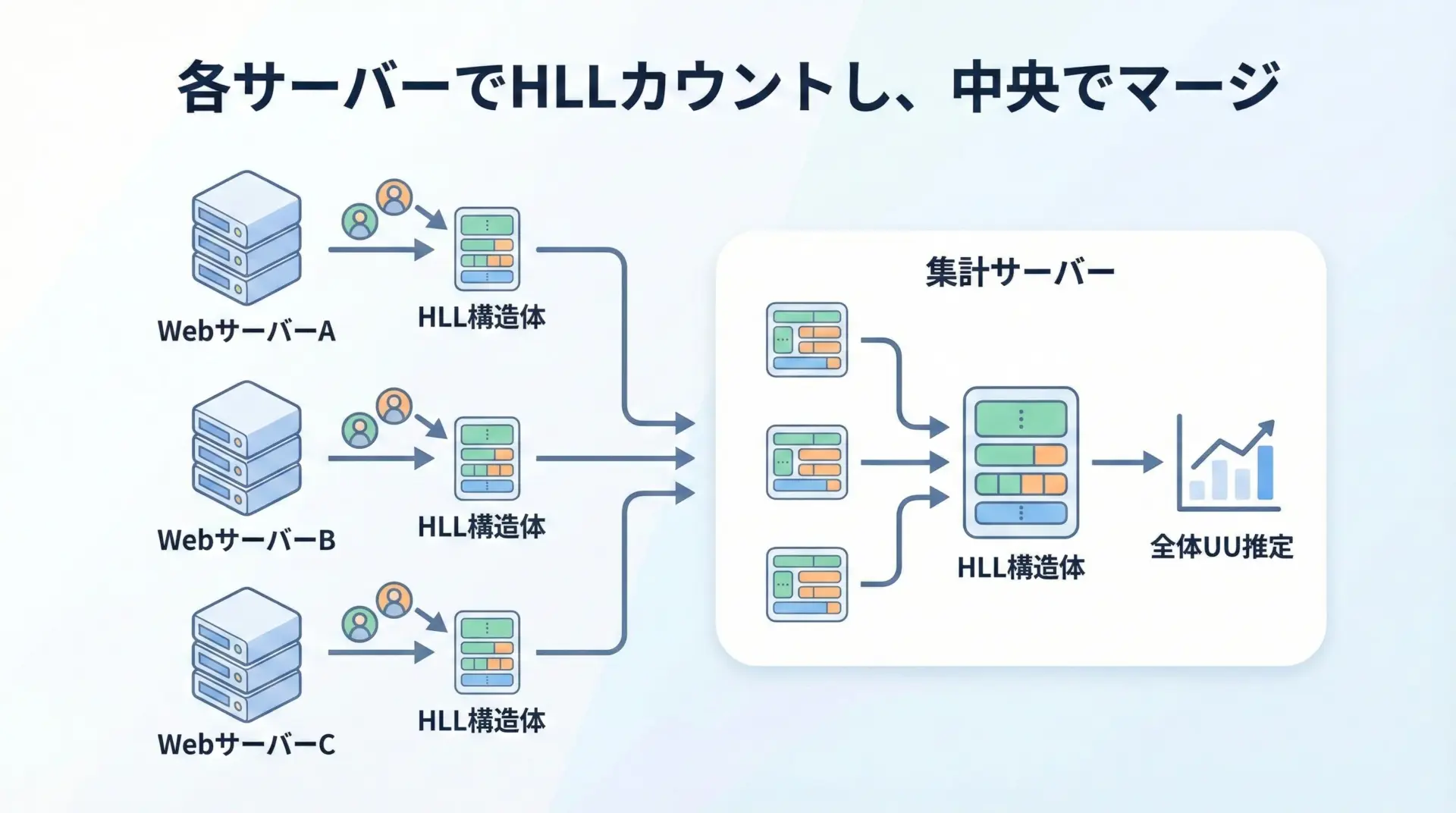
大規模Webサービスでは、トラフィックを複数サーバーに分散して処理することが一般的です。
各サーバーごとにHyperLogLogを持ち、日次・時間単位でユニークユーザーを計測していきます。
最後に、集計用のジョブがすべてのHLLをマージすると、全サービス横断でのユニークユーザー数を安価に算出できます。
ログ分析基盤やDWHでの利用
BigQueryや各種データウェアハウスには、HyperLogLogに相当する近似カウント関数が用意されていることが多いです。
これにより、巨大なテーブルに対して「ユニークユーザー数をとりあえずざっくり見たい」といった分析が気軽に行えます。
このような近似カウントは、速度とコストを重視する探索的分析の初期段階に特に有用です。
ざっくりとした規模感がわかれば、その後に必要に応じて範囲を絞った厳密集計に進むことができます。
HyperLogLogを使うときの実務的なポイント
最後に、実務でHyperLogLogを利用する際に意識しておきたいポイントを整理します。
どの程度の誤差を許容するかを明確にする
HyperLogLogは誤差とメモリのトレードオフで成り立っています。
事前に「このKPIは±何%までズレていても問題ないか」をチームで合意しておくと、レジスタ数の設計や、利用するライブラリ・ミドルウェアの設定を決めやすくなります。
ユニーク数のオーダーを見積もる
想定されるユニーク数のオーダー(10万なのか、1億なのか)によって、必要な精度やメモリ量の感覚も変わります。
オーダーさえ把握しておけば、HyperLogLogの設定値を「やや多め安全側」に振るなどの判断もしやすくなります。
小さな集合には別の方法も検討する
ユニーク数が非常に小さい場合や、厳密な数が欲しい場合には、通常のハッシュセットやビットマップなど別のデータ構造の方が適していることも多いです。
「一定以上のユニーク数になったらHyperLogLogに切り替える」といったハイブリッド構成も現実的な選択肢です。
まとめ
HyperLogLogは、巨大なデータ集合に対するユニークカウントを、わずかなメモリと高速な計算で実現する確率的アルゴリズムです。
その中核となるアイデアは、ハッシュ値の先頭に現れる0の連続長から、統計的に要素数を推定するというものです。
厳密な結果が必要な場面には適していませんが、多くのビジネス指標においては数パーセント程度の誤差は許容されることが多く、その代償として得られるメモリ削減効果・スループット向上・分散集計との親和性は非常に大きな価値を持ちます。
巨大なデータを扱う基盤やプロダクトを設計する際には、「すべてを正確に数える」だけでなく、どこまでを近似で済ませて、どこにリソースを集中させるかという発想が重要になります。
HyperLogLogは、そのような設計思想を体現したアルゴリズムの1つとして、今後もさまざまな場面で活用されていくでしょう。