プログラムを書いていて「スタックオーバーフロー」というエラーに出会い、「いきなり落ちた…何が悪かったんだろう?」と感じたことはないでしょうか。
とくに再帰関数を使ったときに発生しやすく、原因が見えにくいエラーの代表例です。
この記事では、スタックオーバーフローの正体と、再帰のしくみ、それに伴う注意ポイントを、図解イメージを交えながら丁寧に解説していきます。
スタックオーバーフローとは何か
スタックオーバーフローの基本概念
スタックオーバーフローとは、プログラムが使ってよいスタック領域を使い切ってしまい、これ以上データを積めなくなった状態を指します。
多くの言語では、この状態になるとランタイムやOSがプログラムを強制終了させます。
ここでいうスタックは、データ構造としてのスタック(LIFO: Last In, First Out)とほぼ同じ考え方で、関数呼び出しの情報を一時的に保存しておくメモリ領域です。
関数を呼ぶたびに「呼び出し元に戻るための情報」や「ローカル変数」などが積み重なっていきます。
スタックオーバーフローが起きるとき、OSやランタイムは「これ以上スタックを確保したら危険」と判断してプログラムを止めていると考えるとイメージしやすいです。
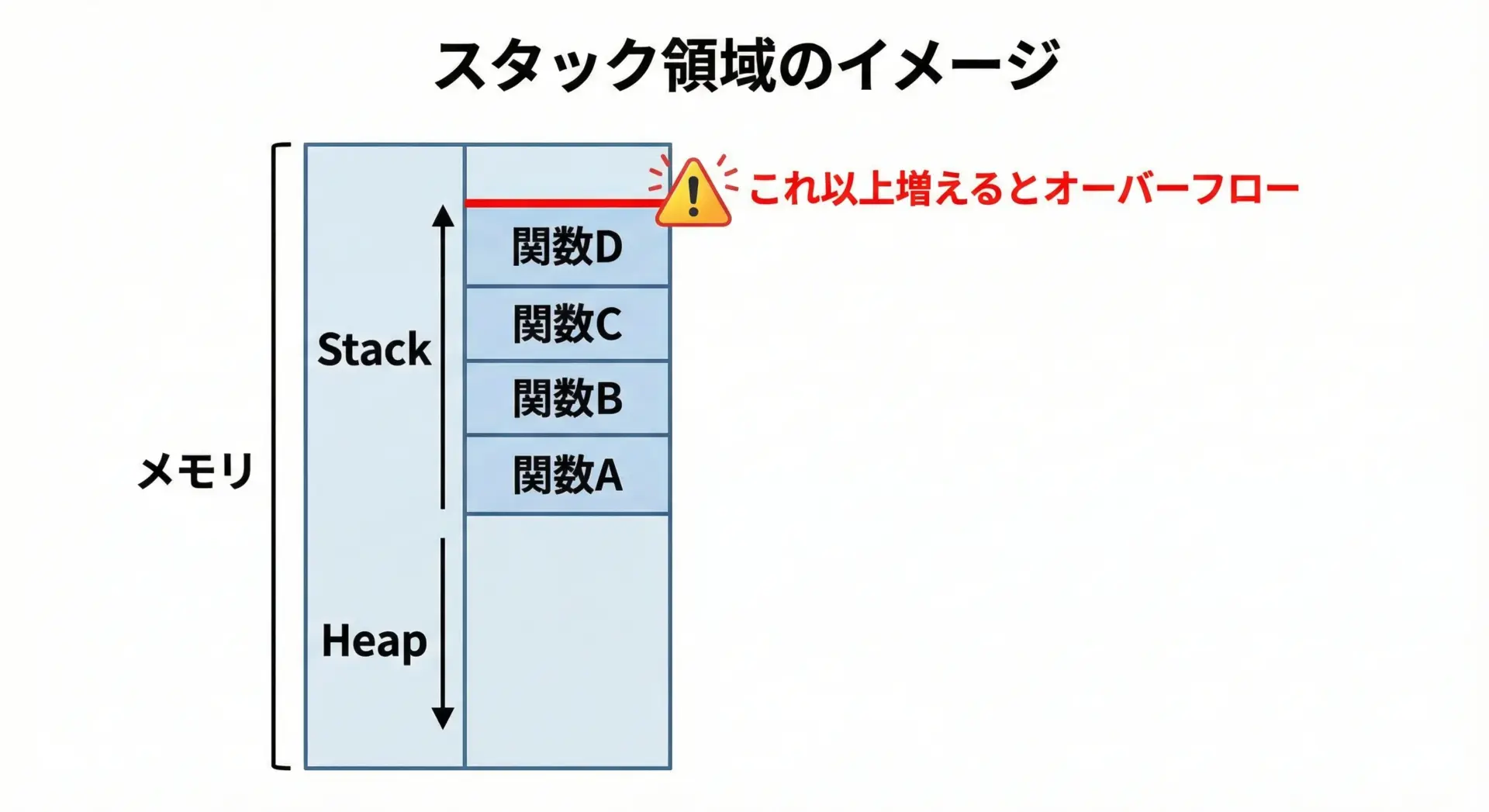
スタックは有限のサイズしかありません。
そのため極端に深い関数呼び出し(とくに誤った再帰)を行うと、いつか必ずスタックオーバーフローが発生します。
関数呼び出しとコールスタックの関係
プログラムが関数を呼び出すたびに、言語処理系やOSはコールスタック(call stack)と呼ばれるスタックに情報を積み上げていきます。
1回の関数呼び出しに対応する情報のかたまりを、しばしばスタックフレーム(stack frame)と呼びます。
スタックフレームにはおおよそ次のような情報が入っています。
- 呼び出し元のアドレス(戻り先)
- 関数の引数
- ローカル変数
- 一時的な計算結果(レジスタ退避など、処理系依存)
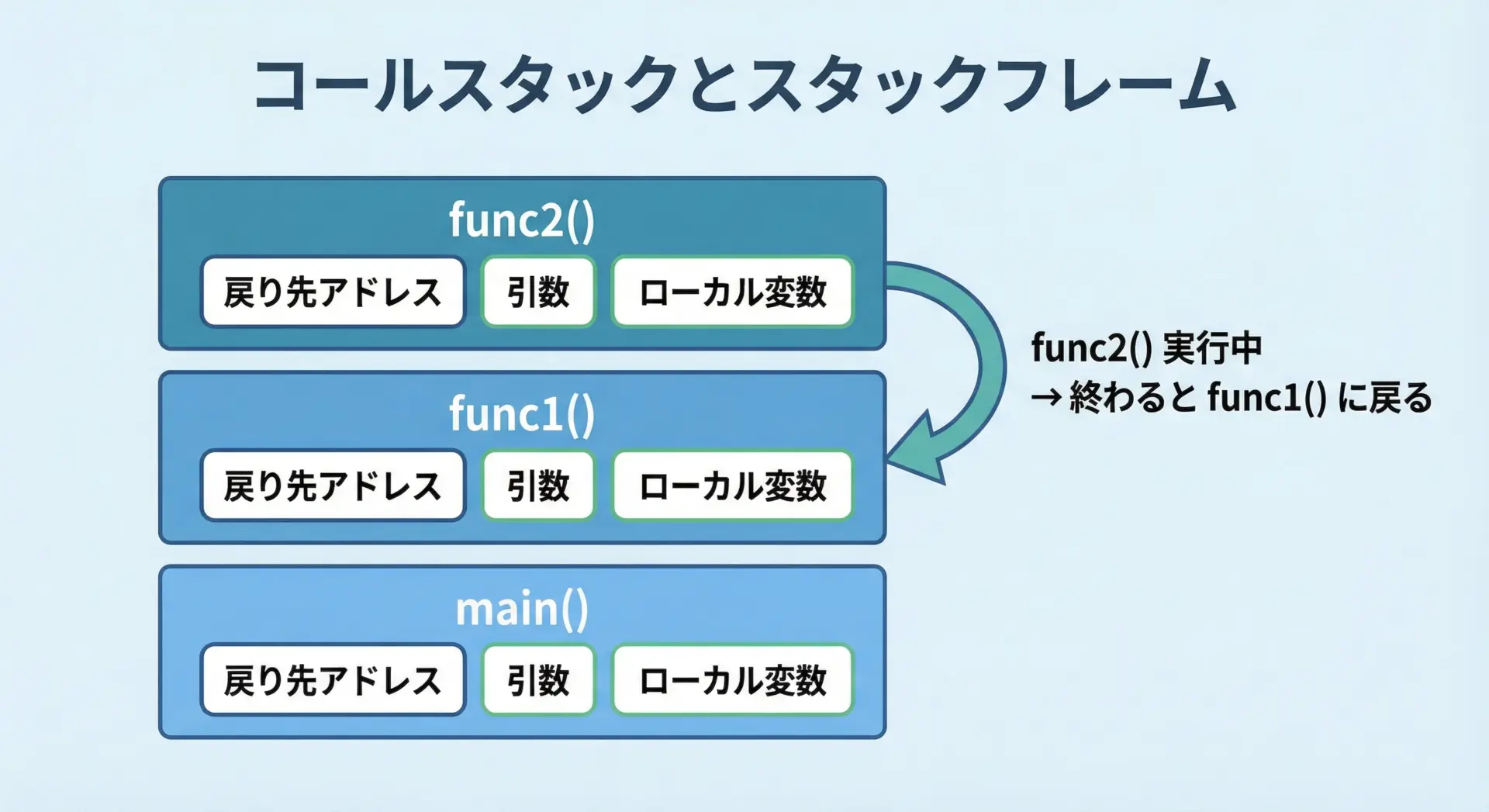
関数が終わると、その関数のスタックフレームはスタックからポップされ、プログラムは呼び出し元のアドレスに戻ります。
「呼び出すと積む」「終わると崩す」というサイクルでスタックは増減しているのです。
スタックオーバーフローが起きる典型パターン
スタックオーバーフローを引き起こしやすい典型パターンには、次のようなものがあります。
1つ目は終了条件がない、または満たされない再帰呼び出しです。
関数が自分自身を呼び続け、永遠に戻ってこられないため、スタックがひたすら積み上がってしまいます。
2つ目は極端に深い再帰です。
たとえば、配列の要素数が100万なのに、それを1要素ずつ再帰で処理しようとするなどが該当します。
論理的にはいつか終わりますが、その前にスタック領域の上限に到達してしまう可能性があります。
3つ目は巨大すぎるローカル変数です。
1回の関数呼び出しで大きな配列や構造体をスタックに確保すると、再帰でなくても数回のネストでスタックを使い切ることがあります。
C言語など低レベル寄りの言語でよく問題になります。
これらに共通するのは「スタックフレームが増え続ける」または「1つ1つのスタックフレームが大きすぎる」という点です。
再帰のしくみを理解する
再帰関数とはどういう関数か
再帰関数とは、自分自身(または互いを呼び合う関数群)を呼び出す関数のことです。
もっともシンプルな例として、次のような擬似コードを考えてみます。
function countdown(n):
if n == 0:
print("end")
return
print(n)
countdown(n - 1)このcountdown関数は、自分の中でcountdownを呼び出しているので、再帰関数です。
再帰のポイントは「問題を少し小さくして、同じ処理を自分にやらせる」という発想にあります。
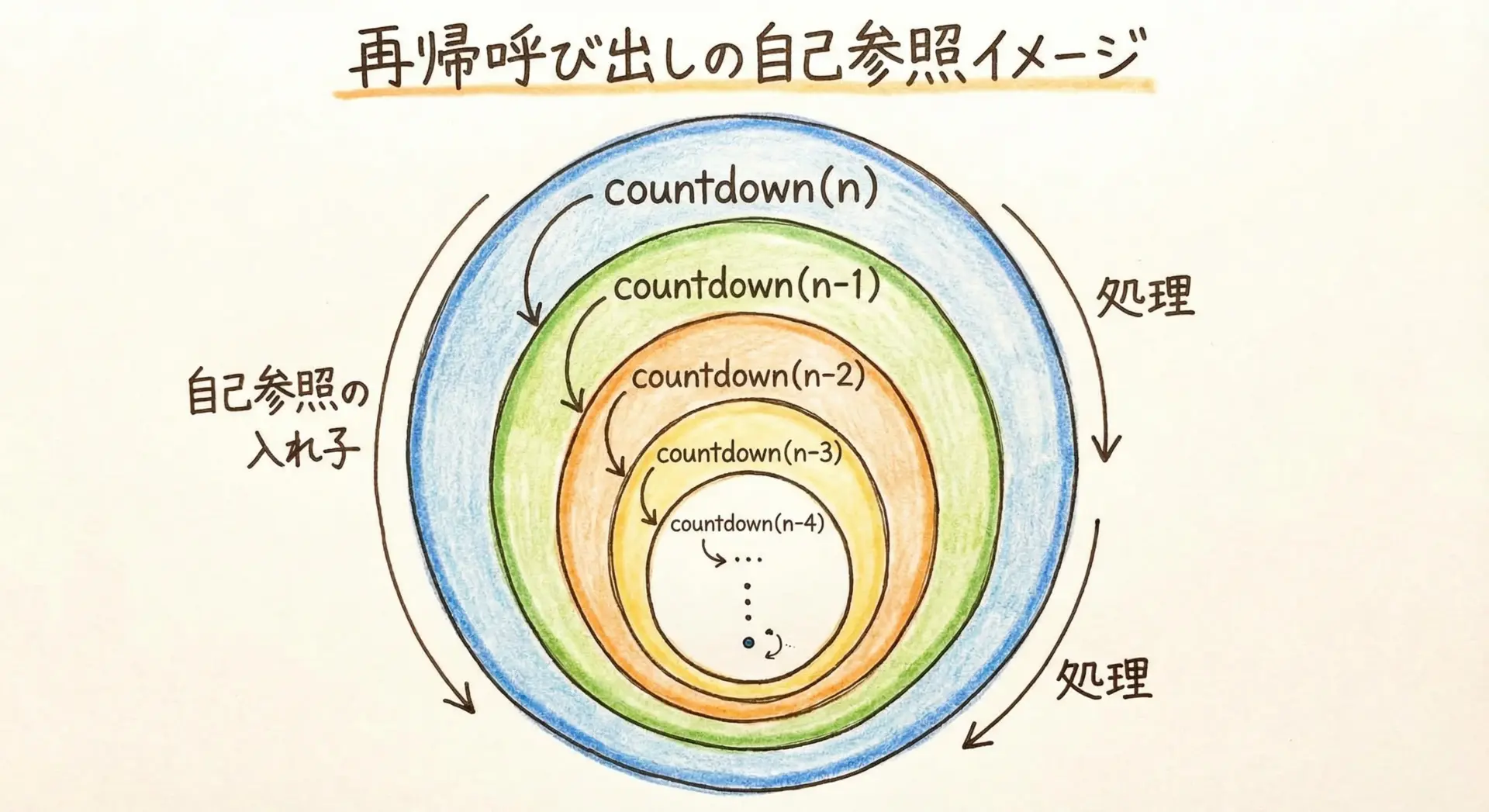
再帰はアルゴリズムをシンプルに書ける反面、コールスタックを多く消費しやすいというリスクも持っています。
そのため、再帰の内側で何が起きているかを理解しておくことが重要です。
ベースケース(終了条件)の役割
再帰関数には必ず「ベースケース」(終了条件)が必要です。
ベースケースとは、「これ以上再帰呼び出しをせずに、直接答えを返す条件」のことです。
先ほどのcountdownでいえば、n == 0がベースケースです。
この条件を満たしたときだけ、再帰呼び出しを行わずにreturnしています。
ベースケースがない、またはベースケースに到達できないロジックになっていると、再帰は必ずスタックオーバーフローに向かって進んでしまいます。
その意味で、ベースケースは「スタックオーバーフローを防ぐ最初の防波堤」といえます。
再帰呼び出しでスタックが増えるしくみ
再帰も普通の関数呼び出しの一種なので、呼び出しごとにスタックフレームが積まれます。
違いは、同じ関数名のスタックフレームが何段にも積み重なる点です。
countdown(3)を例に、コールスタックの状態を追ってみます。
countdown(3)を呼ぶ3 != 0なのでcountdown(2)を呼ぶ(新しいスタックフレームが積まれる)2 != 0なのでcountdown(1)を呼ぶ1 != 0なのでcountdown(0)を呼ぶ0 == 0なので「end」を表示してreturnし、1つ上のcountdown(1)に戻るcountdown(1)が終了し、さらにcountdown(2)に戻る- 最後に
countdown(3)に戻り、全体が終了する
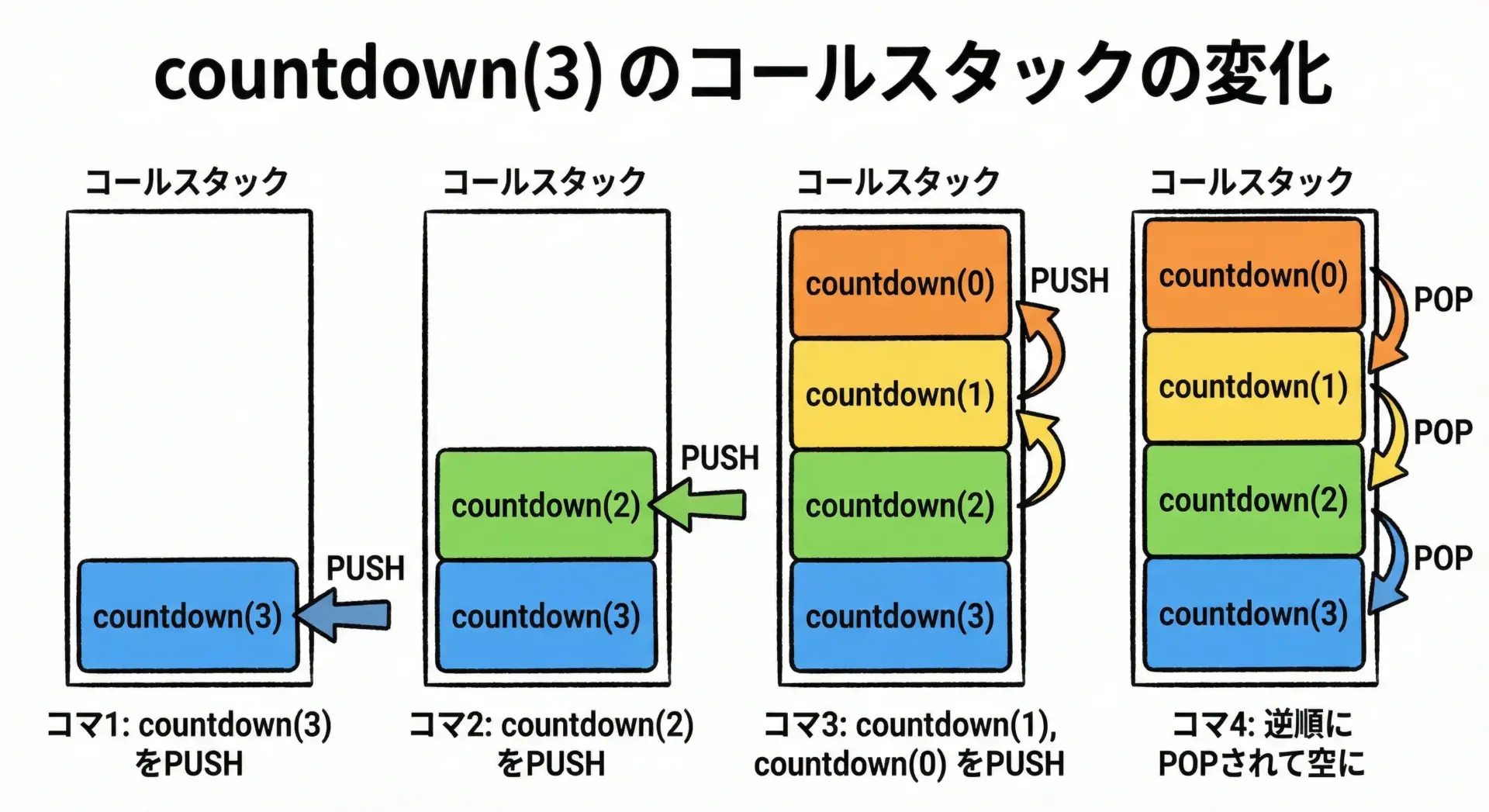
このように再帰の深さが1増えるたびに、スタックフレームが1つ追加されるため、深い再帰ではスタック消費量が急激に増えることになります。
再帰とループ(while/for)の違い
再帰とループは、できることの観点ではほぼ同じ表現力を持ちます。
多くの再帰処理はwhileやforで書き換えることが可能です。
違いのポイントを整理すると、次のようになります。
- 再帰
- メリット: アルゴリズムを簡潔・直感的に書きやすい(特に木構造、分割統治など)
- デメリット: 呼び出しごとにスタックフレームを消費し、スタックオーバーフローのリスクがある
- ループ
- メリット: スタックを増やさず、1つのスタックフレーム内で繰り返し処理できる
- デメリット: 再帰に比べてコードがやや複雑になる場合がある
countdownをループで書き直すと、次のようになります。
function countdown_loop(n):
while n != 0:
print(n)
n = n - 1
print("end")こちらは関数呼び出しは1回だけで、その中でnの値だけを書き換えているため、スタックフレームが増えません。
深い再帰が必要そうな処理は、ループに書き換えられないかを検討することが、スタックオーバーフロー回避のひとつのコツです。
スタックオーバーフローが起きる再帰の例
ベースケースを忘れた再帰の例
ベースケースを忘れた再帰は、スタックオーバーフローの典型です。
簡単な例として、次のような擬似コードを考えます。
function infinite():
print("call")
infinite()この関数には終了条件が一切ありません。
infinite()を1回呼ぶと、永久に自分自身を呼び続けます。

実際には無限に続く前に、スタック領域が尽きてスタックオーバーフローになります。
ベースケースの有無は、再帰を書くときに真っ先に確認すべきポイントです。
終了条件が満たされないロジックの例
ベースケースらしき条件があっても、ロジックのミスでベースケースに到達できない場合も危険です。
function countdown_bug(n):
if n == 0:
print("end")
return
print(n)
countdown_bug(n + 1) // バグ: n を減らさずに増やしている一見するとn == 0がベースケースに見えますが、countdown_bugはnを減らすのではなく増やしています。
そのため、正の整数からスタートするとnは0に近づかず、ベースケースに一生到達しません。
この種のバグは、再帰関数の引数をどのように変化させているかを追うことで発見できます。
「再帰を呼ぶ前後で、ベースケースに向かって値が変化しているか」をチェックすることが重要です。
深すぎる再帰とスタックサイズの限界
ベースケースもロジックも正しくても、深さが大きすぎる再帰はスタックオーバーフローを起こす可能性があります。
たとえば、次のような「1からNまで足し合わせる」関数を考えます。
function sum_to_n(n):
if n == 0:
return 0
return n + sum_to_n(n - 1)ロジックとしては正しいですが、nが100万や1000万といった大きな値になると、再帰の深さもその分だけ深くなり、多くの言語・環境でスタックの上限を超える可能性があります。
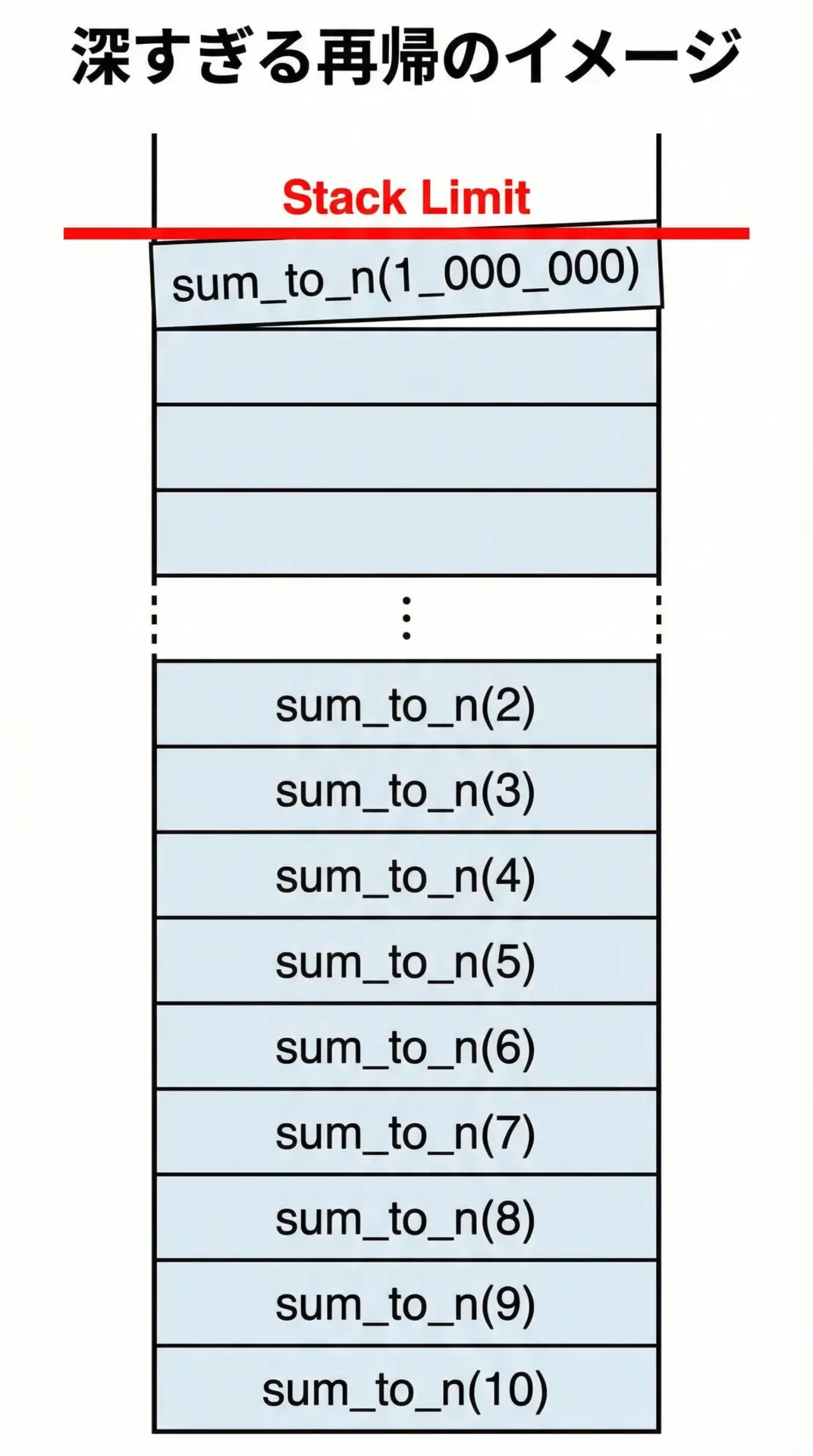
スタックサイズの上限は、OSや言語処理系、スレッド設定などによって異なります。
たとえばC/C++やJavaではスレッドごとにスタックサイズが決まっており、Pythonなどの言語では再帰の深さに明示的な制限を設けていることもあります。
デバッガやログで再帰の深さを確かめる方法
スタックオーバーフローを防ぐには、自分の再帰がどのくらいの深さまで潜っているかを把握することが有効です。
そのための方法として、デバッガやログ出力を活用します。
ひとつの方法は、再帰の引数とは別に「深さ」を表すパラメータを持たせるやり方です。
function recurse(n, depth):
print("depth =", depth, "n =", n)
if n == 0:
return
recurse(n - 1, depth + 1)このようにしてログを取れば、スタックオーバーフローが起きる前に「どこまで深く潜っているのか」を観察できます。
もうひとつは、IDE 付属のデバッガを使って「コールスタックビュー」を確認する方法です。
ブレークポイントを設定して再帰関数を止め、コールスタックを表示すると、同じ関数がどれだけの段数積み重なっているかが一目でわかります。

ログとデバッガを組み合わせることで、「想定外に深く潜っていないか」「ベースケースにきちんと到達しているか」を確認しやすくなります。
再帰でスタックオーバーフローを防ぐポイント
安全なベースケースの設計と確認方法
スタックオーバーフローを避けるうえで、最初に注目すべきはベースケースの設計です。
安全なベースケースを考えるときには、次の3点を意識するとよいでしょう。
1つ目は、「必ず到達できる条件か」を考えることです。
引数や状態がどのように変化していくかを紙に書き出し、有限回のステップでベースケースに到達することを確認します。
2つ目は、複数の入り口からの呼び出しを想定することです。
関数が複数の場所から様々な引数で呼ばれる場合、それぞれのケースでベースケースに到達するかを確認します。
特に負の値や空配列などの「境界値」を忘れないことが重要です。
3つ目は、テストケースで境界条件を重点的に検証することです。
たとえば、次のような観点でテストします。
- 最小の入力(0、空リストなど)
- 典型的な入力(小さめの正数や短いリスト)
- 想定上限に近い大きな入力
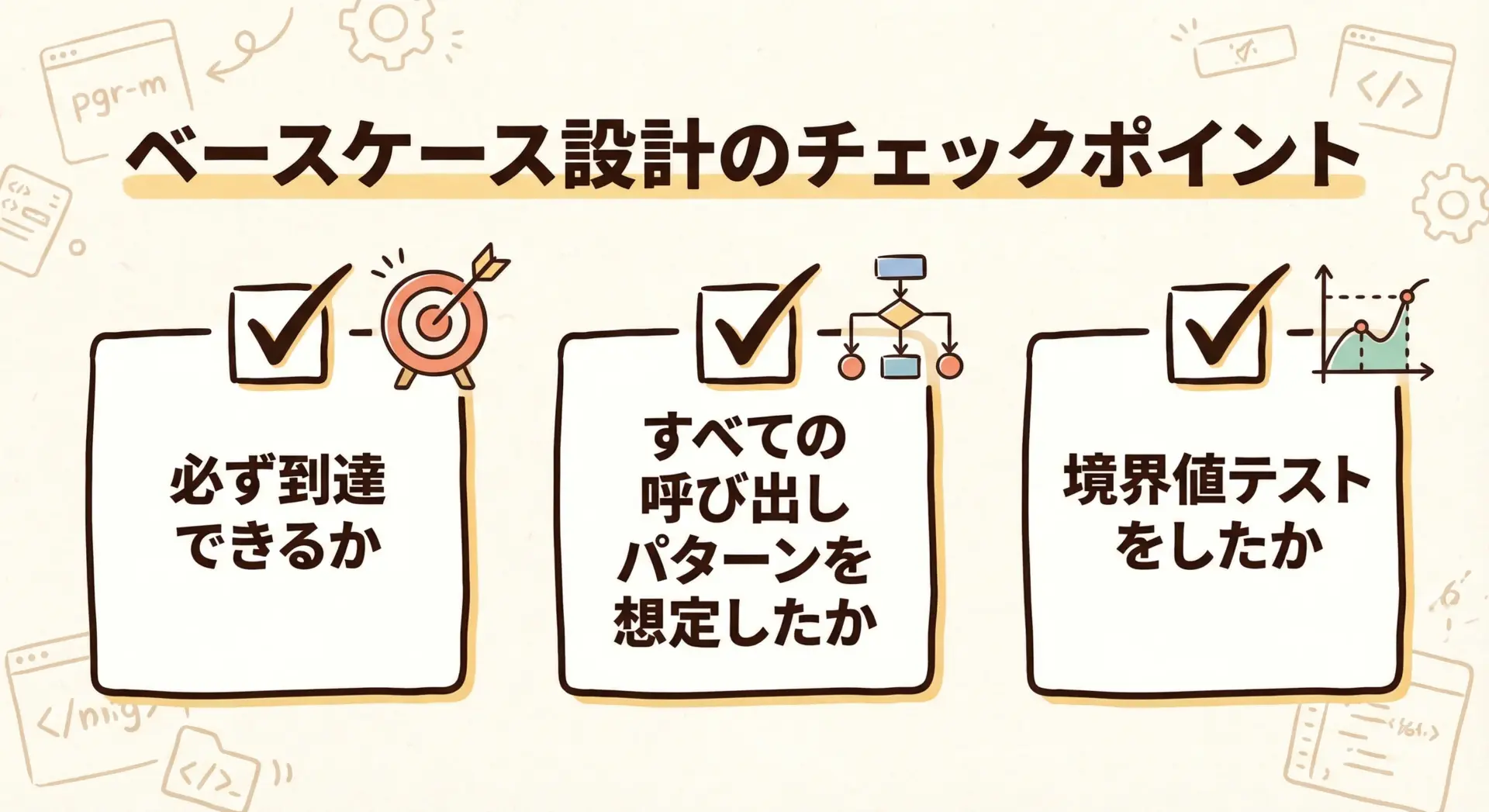
再帰を書くときは「まずベースケースから書く」習慣をつけると、安全性が高まります。
再帰をループに書き換える判断基準
再帰は強力ですが、常に再帰が最適な選択とは限りません。
スタックオーバーフローを避けるために、ループへの書き換えを検討すべき場面があります。
判断基準として、次のような観点が挙げられます。
- 再帰の深さが入力サイズに比例して増えるか
例えば、配列の長さNに対して深さNの再帰になる場合、Nが大きいとスタックリスクが高まります。こうした線形の深さの再帰は、多くの場合ループに書き換え可能です。 - 再帰で状態をほとんど持たないか
単に「カウンタを1ずつ増減させているだけ」のような再帰は、スタックフレームに特別な情報を載せていないので、ループでも同じことができます。 - 言語や環境に再帰深さの制限があるか
PythonやJavaScriptなどでは再帰の深さに制限があることが多く、大きなデータを処理するアルゴリズムではループのほうが安全です。
一方で、木構造の探索や分割統治アルゴリズム(クイックソートなど)は、再帰で書くと非常に読みやすくなる場合があります。
その場合でも、最大深さの見積もりと入力データのスケールを考慮して、スタックサイズに収まるかを意識しておくことが大切です。
テイル再帰最適化とその限界
一部の言語やコンパイラは、テイル再帰最適化(tail call optimization, tail recursion optimization)という仕組みを持っています。
これは、「関数の最後の処理が、単に別の関数(しばしば自分自身)を呼び出すだけ」の場合に、スタックフレームを増やさずに呼び出しを行うという最適化です。
テイル再帰の例を擬似コードで示します。
function sum_tail(n, acc):
if n == 0:
return acc
return sum_tail(n - 1, acc + n)この関数では、sum_tailの最後の処理がそのままreturn sum_tail(...)になっています。
もし言語処理系がテイル再帰最適化を行ってくれれば、ループのようにスタックを増やさずに動作させることが可能です。
しかし、テイル再帰最適化にはいくつかの限界があります。
- すべての言語・処理系でサポートされているわけではない
たとえば、Javaや標準的なPythonはテイル再帰最適化を行いません。関数型言語や一部のコンパイラでのみサポートされます。 - テイル位置でない再帰には効かない
再帰呼び出しの「後ろに処理が残っている」場合は、テイル再帰とはみなされません。
function sum_not_tail(n):
if n == 0:
return 0
return n + sum_not_tail(n - 1) // 再帰のあとに「+ n」が残っているこのような再帰は、テイル再帰最適化の対象外です。
- 最適化に頼りすぎると可搬性が落ちる
ある処理系では動いても、別の環境ではスタックオーバーフローになる可能性があります。
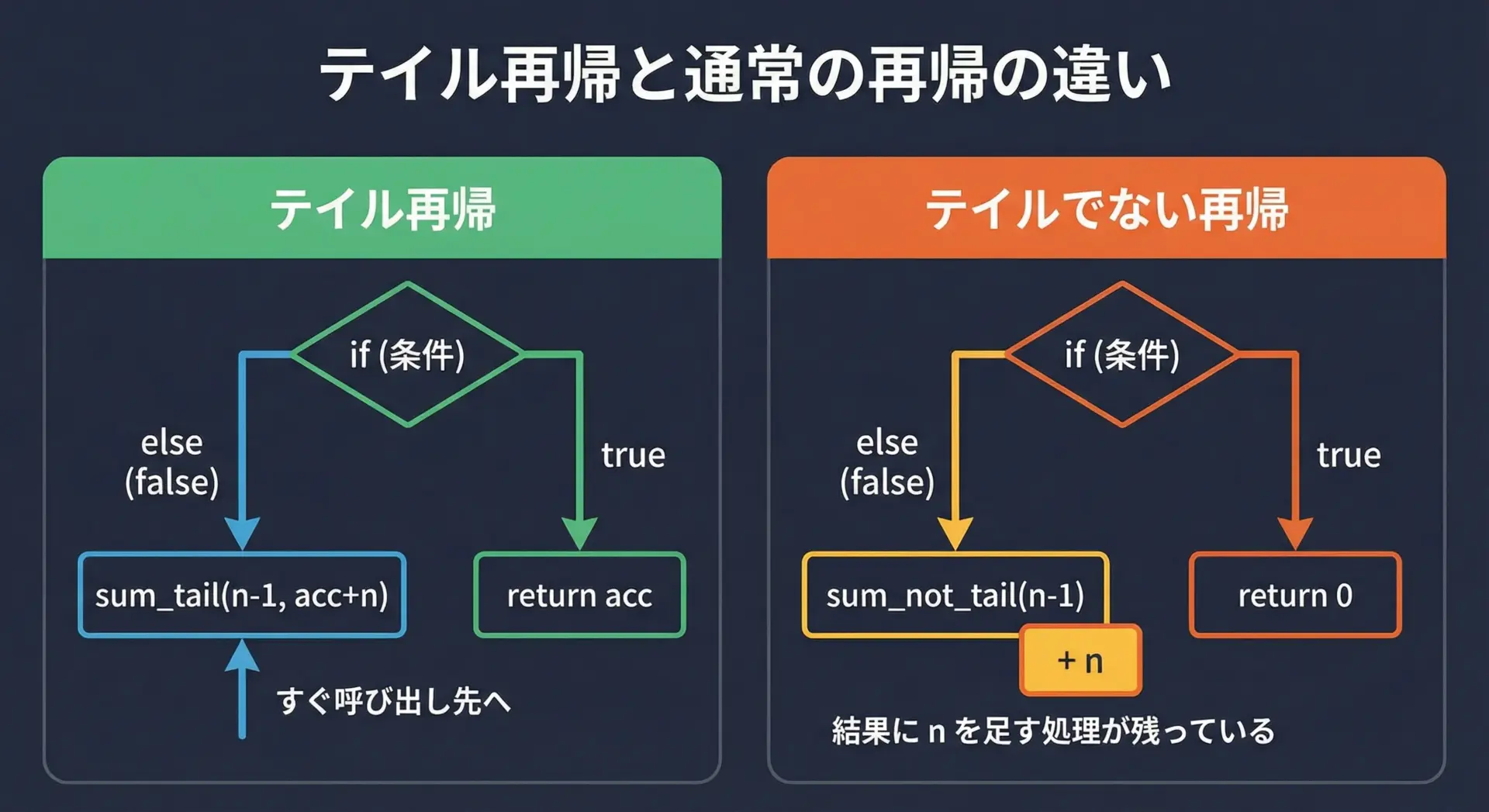
テイル再帰最適化は「あれば嬉しいボーナス」程度に考え、基本はループへの書き換えなどでスタックオーバーフローを防ぐほうが堅実です。
初心者が再帰を使うときのチェックリスト
再帰に慣れていないうちは、毎回同じ観点でコードをチェックする習慣が役立ちます。
以下は、そのためのシンプルなチェックリストです。
- ベースケースは明示的に書かれているか
- 「これはベースケース」と自分で指させる条件があるか確認します。
- すべての呼び出し経路で、有限回のステップでベースケースに到達するか
- 引数の変化をシミュレーションしてみて、増え続けるだけになっていないかを見ます。
- 再帰1回ごとに、問題サイズは十分に小さくなっているか
- 配列なら長さ、数値なら値の大きさなどが、確実に減っているかを確認します。
- 最大の再帰深さを概算してみたか
- 「最悪ケースで何回くらい再帰されるだろう?」と見積もり、それがスタックに収まりそうかを考えます。
- ループで書いたほうがシンプル・安全にならないか検討したか
- とくに線形な深さの再帰は、ループにしてしまうほうが安全なことが多いです。
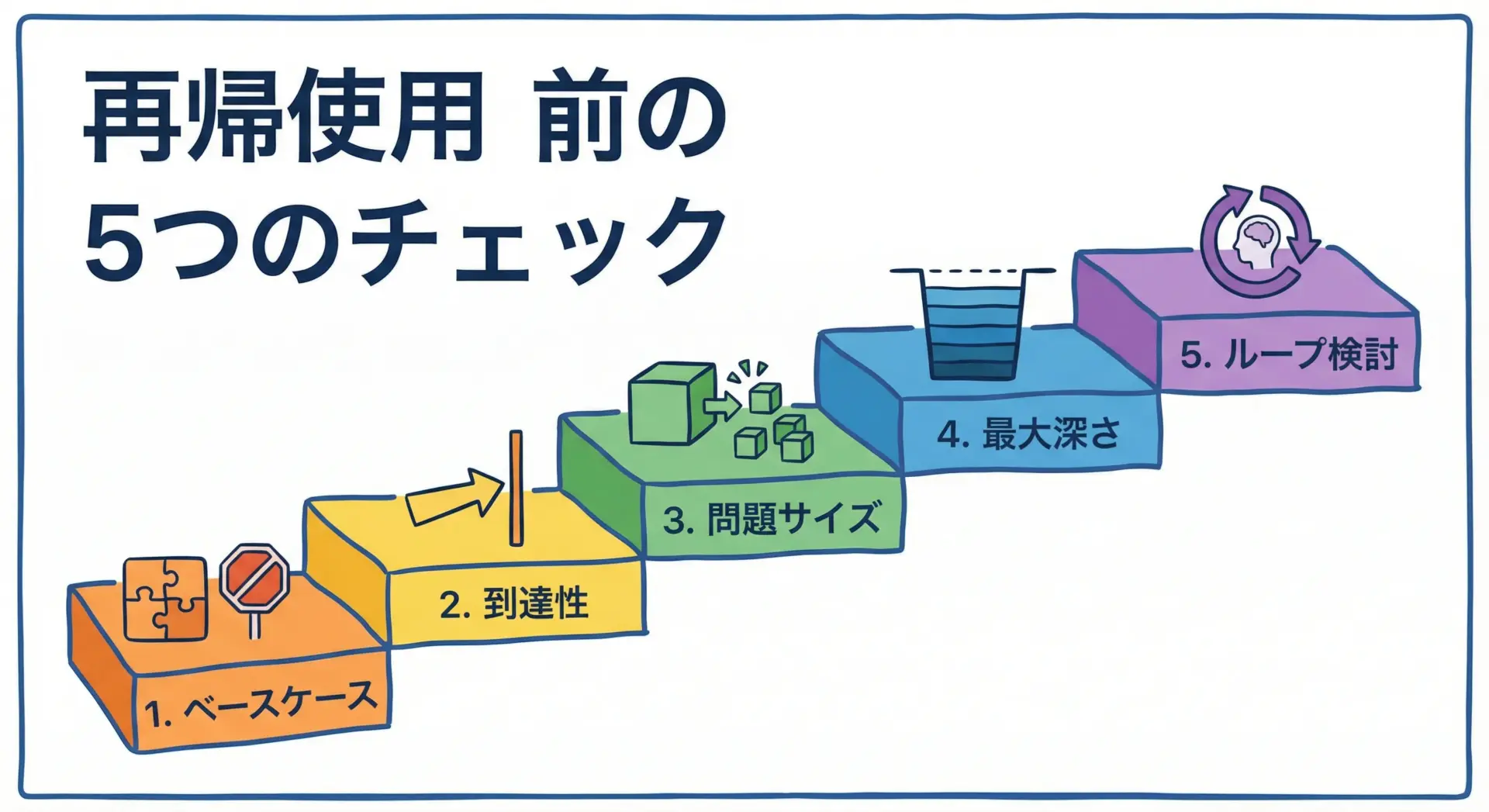
このようなチェックを習慣化することで、スタックオーバーフローだけでなく、論理バグも見つけやすくなります。
まとめ
スタックオーバーフローは、単なる「よくわからないエラー」ではなく、有限なスタック領域を再帰や深い関数呼び出しで使い切ってしまった結果として生じる、きわめて論理的な現象です。
スタックフレームやコールスタックのイメージを理解すると、「なぜ再帰で落ちやすいのか」「どこを直せばよいのか」が見えやすくなります。
再帰は、木構造や分割統治アルゴリズムなどで非常に強力な表現力を発揮しますが、その一方でベースケースの設計ミスや、深さの見積もり不足がスタックオーバーフローの原因にもなります。
ベースケースを丁寧に設計し、引数の変化と最大深さを意識し、必要に応じてループやテイル再帰最適化を活用することが、安定したコードへの近道です。
「スタックオーバーフローで落ちた」という経験は、再帰とメモリのしくみを深く理解するチャンスでもあります。
この記事で紹介した考え方やチェックポイントを手がかりに、自分のコードの内部で何が起きているかを意識しながら、再帰との付き合い方を少しずつ身につけていってみてください。

