コンピュータは2進数で計算していますが、人間は10進数で数を扱います。
このギャップを埋める工夫の1つがBCD(二進化十進数)表現です。
電卓や金融系システム、組み込み機器などで、10進数をそのままの桁で正確に扱いたいときに使われます。
この記事では、BCDの基本的な仕組みから、通常の2進数との違い、具体的な使われ方まで、初心者にも分かりやすく解説していきます。
BCD(二進化十進数)表現とは
BCDの基本アイデア
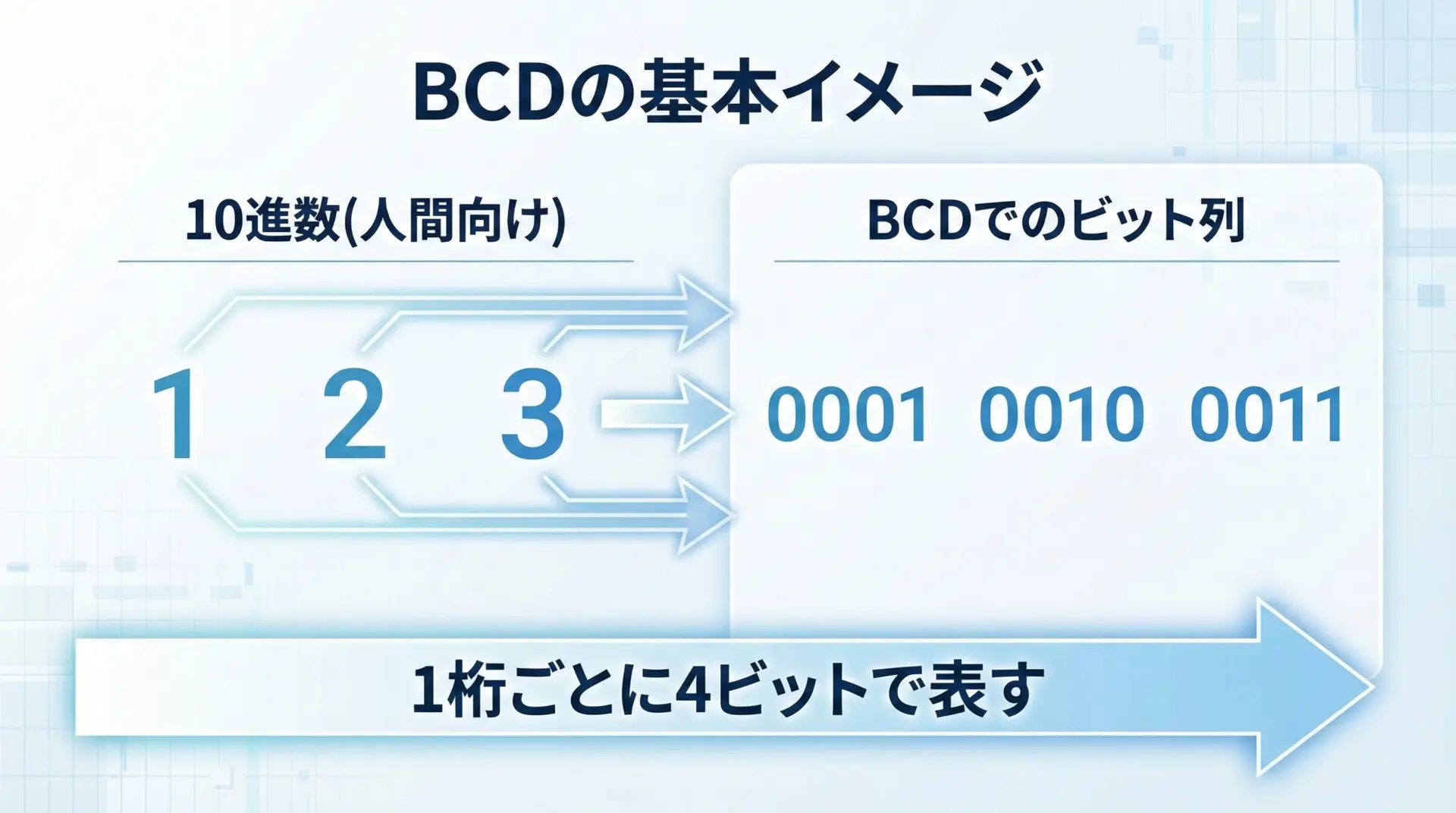
BCD(二進化十進数)表現とは、10進数の各桁を、それぞれ独立した4ビットの2進数で表現する方式です。
例えば、10進数の「5」は4ビットの0101で表し、「9」は1001で表します。
通常の2進数では、数値そのものを2進数に変換して1つのビット列にしますが、BCDでは次のような特徴があります。
- 10進数の各桁(0〜9)を、それぞれ4ビット(0000〜1001)で表す
- 10〜15に相当するビット列(1010〜1111)は、基本的には使わない
- 桁が増えると、4ビット単位でどんどん増えていく
「10進数の桁構造を、そのまま2進数に持ち込んだ形式」と考えると分かりやすいです。
BCDの表のイメージ
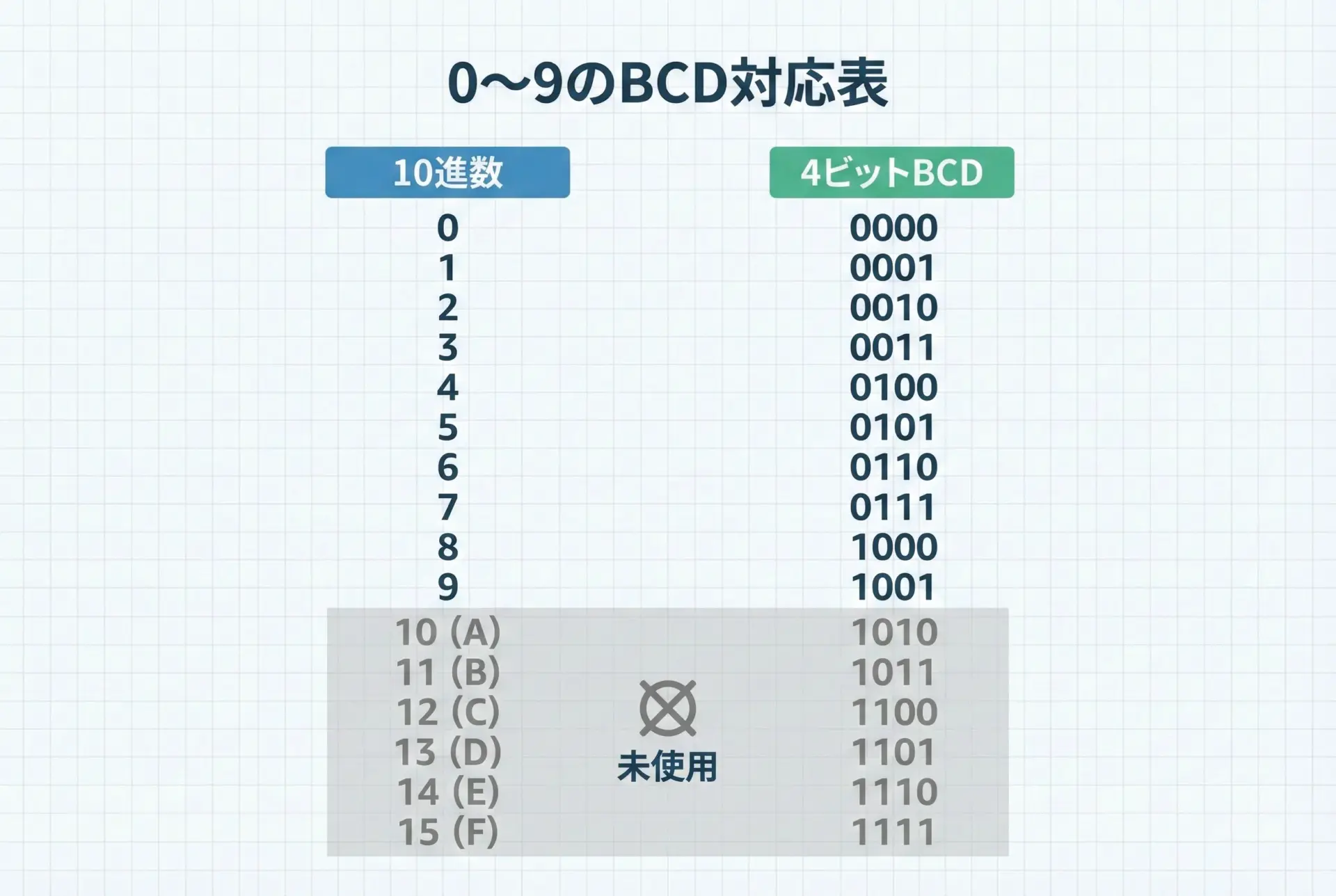
BCDで使う4ビットと10進数の対応は次のようになります。
| 10進数の桁 | BCD(4ビット2進数) |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
この表から分かるように、1桁の10進数は、必ず4ビットで表現されることになります。
通常の2進数との違い
同じ数でもビット列が違う
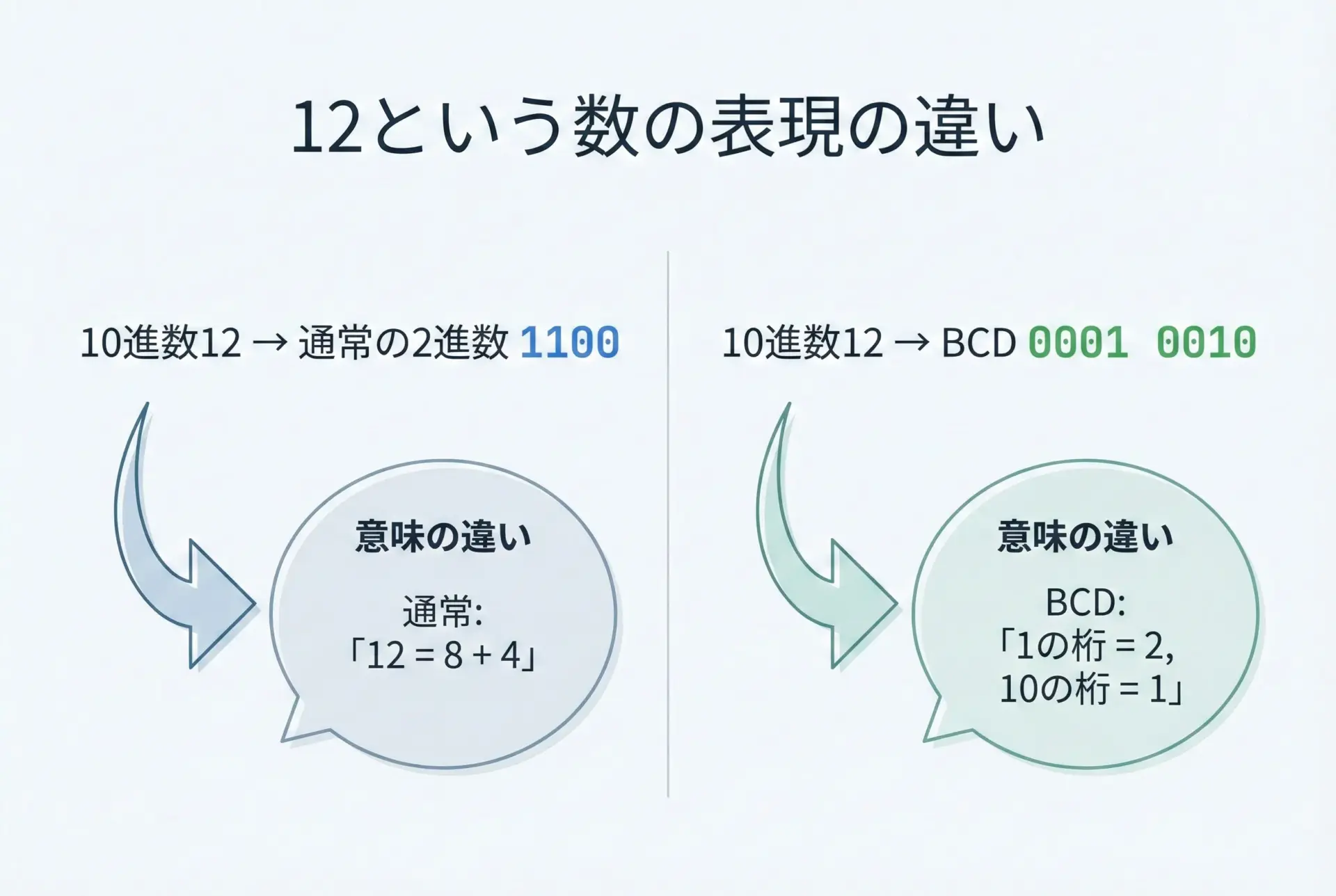
例として、10進数の「12」を考えてみます。
- 通常の2進数表現では、12は
1100(2)です - BCD表現では、「1」と「2」をそれぞれ4ビットで表すため、
0001 0010となります
ここで重要なのは、同じ10進数でも、通常の2進数とBCDではビット列の意味がまったく違うという点です。
- 通常の2進数: ビット全体で「12」という値を表している
- BCD: 左の4ビットが「1」、右の4ビットが「2」という桁情報を持っている
情報量と無駄なパターン
4ビットが表せるパターンは16通り(0〜15)ですが、BCDで実際に使うのは0〜9だけです。
残りの6パターン(10〜15にあたる1010〜1111)は未使用になります。
このため、通常の2進数と比べると、次のような性質があります。
- 同じ範囲の数を表すのに、ビット数が増えやすい
- その代わり、桁ごとの処理や表示が非常に簡単になる
具体例で見るBCD表現
1桁の例
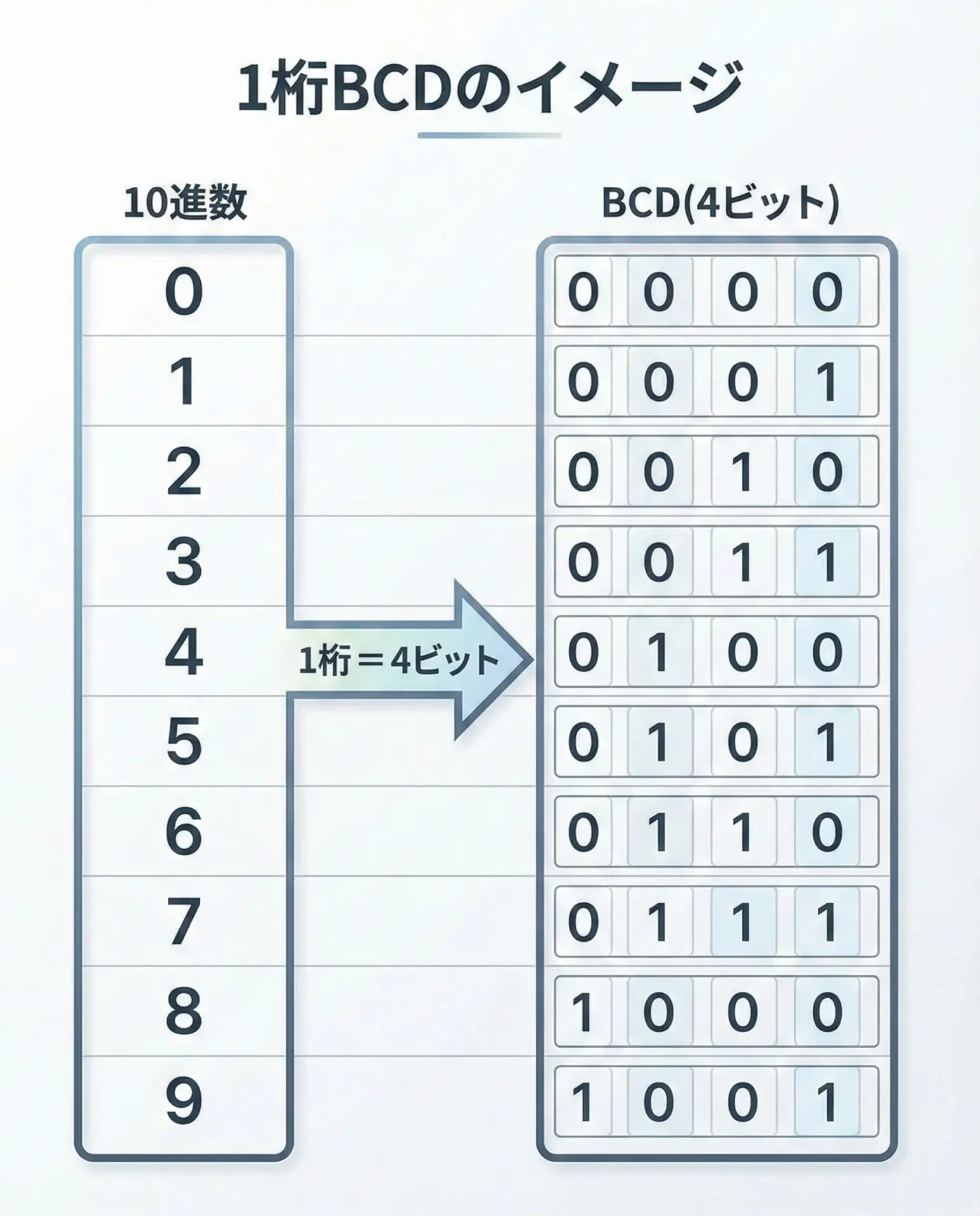
1桁の10進数は、先ほどの表のとおり、次のようになります。
- 0 →
0000 - 5 →
0101 - 9 →
1001
ここまでは通常の2進数と同じですが、BCDの本領は桁数が増えたときに現れます。
複数桁の例(「259」の場合)
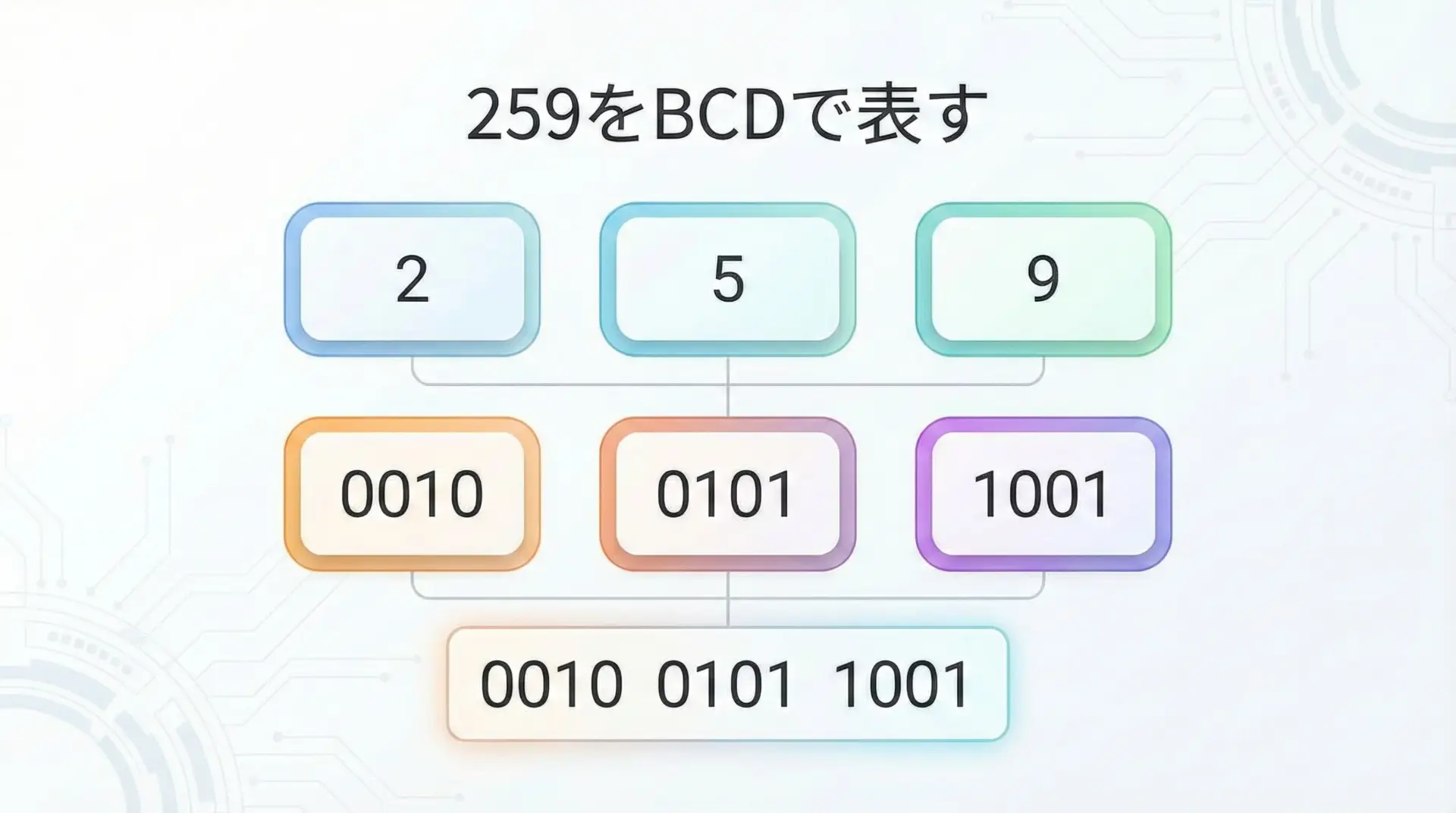
10進数の「259」をBCDで表す流れを見てみます。
- 各桁に分解する
- 100の位: 2
- 10の位: 5
- 1の位: 9
- 各桁を4ビットの2進数にする
- 2 →
0010 - 5 →
0101 - 9 →
1001
- 2 →
- 並べて1つのビット列にする
- BCD表現:
0010 0101 1001
- BCD表現:
「259」をそのまま2進数に変換した100000011(2)とは、まったく違うビット列になることが分かります。
BCDの種類(パックドBCDとアンパックドBCD)
2つの表現方法
BCDには、ビットの詰め方の違いによって、よく使われる2つの形があります。
| 名前 | 概要 |
|---|---|
| パックドBCD | 4ビットを2つまとめて1バイトに詰める |
| アンパックドBCD | 1桁を1バイトで表す(上位4ビットは0など) |
どちらも「1桁=4ビット」という考えは同じですが、メモリの使い方が少し違います。
パックドBCDのイメージ
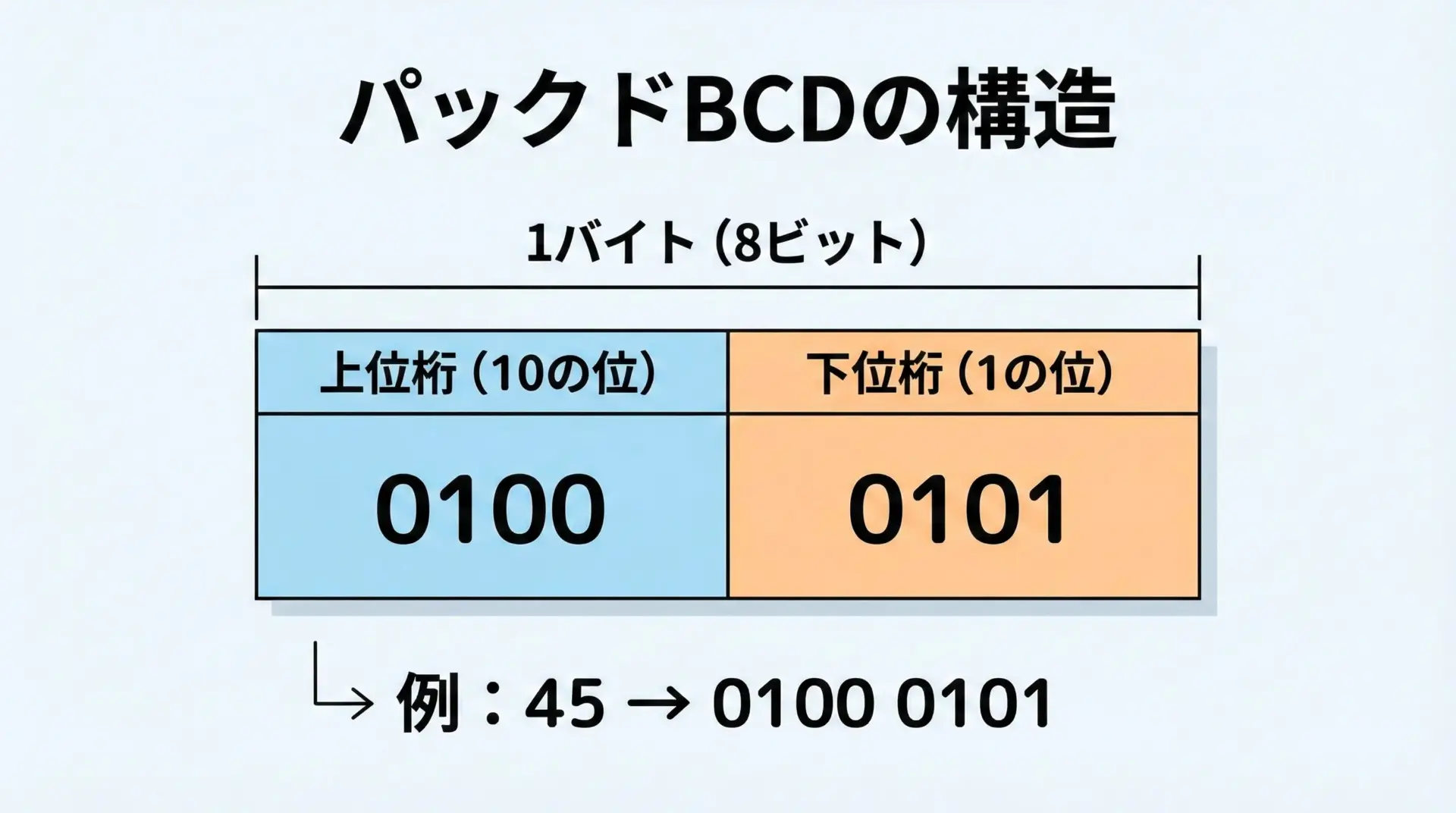
パックドBCDでは、1バイトの中に2桁分のBCDを詰め込みます。
例えば、「45」をパックドBCDで表すと次のようになります。
- 4 →
0100 - 5 →
0101 - まとめて1バイト:
0100 0101
この方式は、桁数が多い金額や数値をコンパクトに保存したいときに使われます。
アンパックドBCDのイメージ
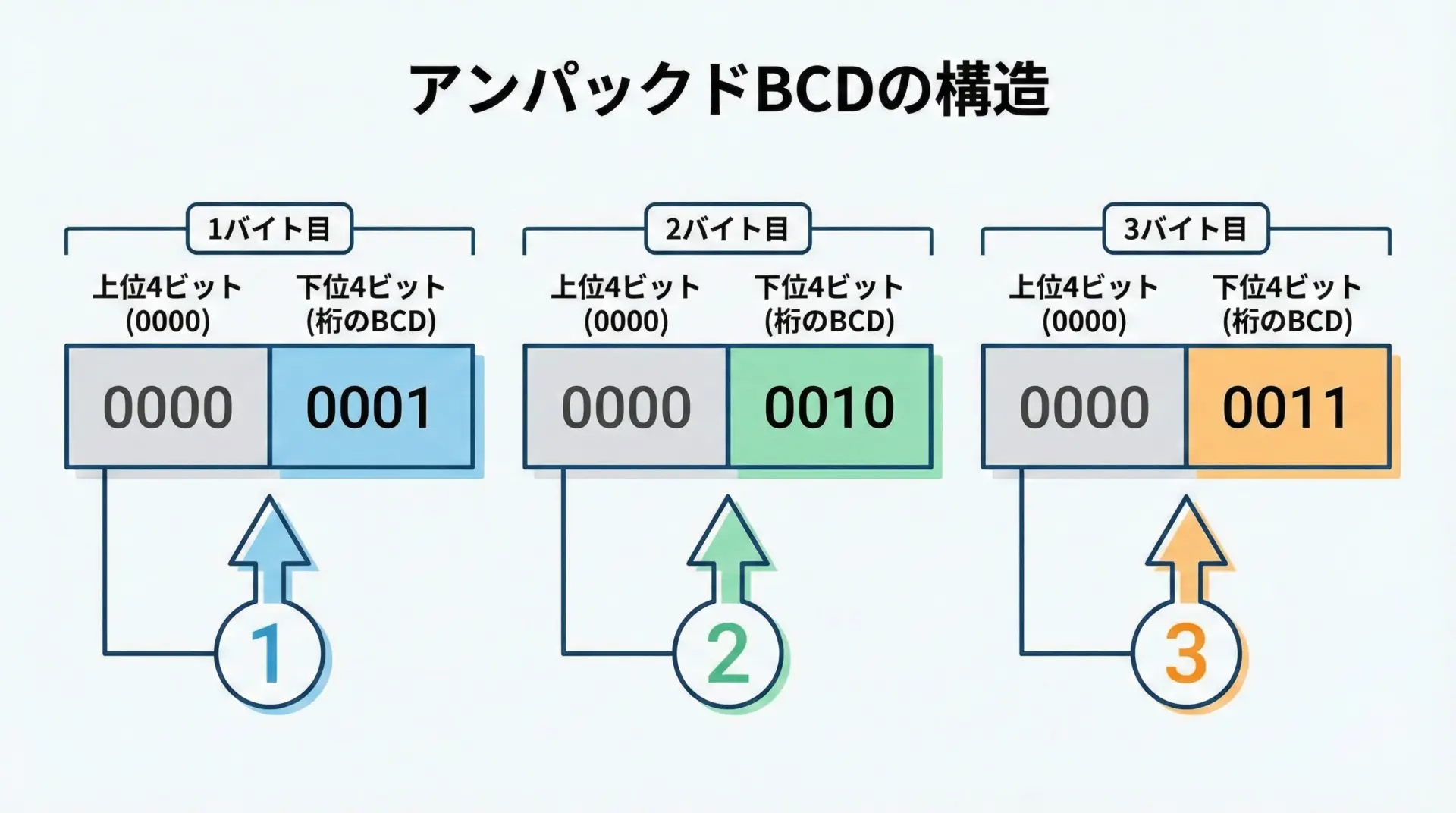
アンパックドBCDでは、1桁を1バイトで表現します。
上位4ビットは0や符号などに使われることが多く、下位4ビットに桁の値が入ります。
例として、「123」をアンパックドBCDで保存すると、次の3バイトになります。
- 1 →
0000 0001 - 2 →
0000 0010 - 3 →
0000 0011
パックドよりはメモリを多く使いますが、1バイト=1文字という感覚で扱いやすいため、文字列と相性が良い形式です。
BCDが使われる理由と用途
なぜ普通の2進数ではなくBCDを使うのか
BCDを使う主な理由は、「10進数の桁を崩さずに、誤差なく扱いたい」からです。
通常の2進数表現では、特に小数や金額を扱うときに、次のような問題が出やすくなります。
- 1や0.01といった数が、2進数ではきれいに表現できない
- そのため、浮動小数点計算で微小な誤差が積み重なってしまう
BCDは、各桁が0〜9の整数として扱われるため、10進数としての「桁」がそのまま保たれ、丸め誤差を極力避けられるという利点があります。
代表的な用途
BCDは、次のような場面でよく使われます。
- 電卓、計算機
- 金融・会計系のシステム(通貨、金額を扱う処理)
- 組み込み機器の表示部(時計、メーターなど)
- 古いメインフレーム系のデータ形式(COBOLなど)
特に「人が見る10進数表示がそのまま重要になる」分野では、いまでもBCDや、それに近い10進数ベースの表現が使われています。
C言語でBCDを扱う簡単なサンプル
整数をBCDに変換する(パックドBCD)
ここでは、10進整数(0〜99)をパックドBCD(1バイト)に変換する簡単なC言語のサンプルを示します。
#include <stdio.h>
// 0〜99の10進整数を、1バイトのパックドBCDに変換する関数
// 例: 45 → 0x45 (4が上位4ビット、5が下位4ビットに入る)
unsigned char dec_to_packed_bcd(unsigned int value) {
// 0〜99の範囲に制限する(それ以外は0にしてしまう)
if (value > 99) {
value = 0;
}
// 10の位と1の位を取り出す
unsigned int tens = value / 10; // 10の位
unsigned int ones = value % 10; // 1の位
// 10の位を上位4ビットに、1の位を下位4ビットに詰める
// (tens << 4) で、10の位を左に4ビットシフト
// 下位4ビットには1の位をそのまま入れる
unsigned char bcd = (unsigned char)((tens << 4) | ones);
return bcd;
}
// パックドBCDを10進整数に戻す関数
unsigned int packed_bcd_to_dec(unsigned char bcd) {
// 上位4ビットが10の位、下位4ビットが1の位
unsigned int tens = (bcd >> 4) & 0x0F; // 上位4ビットを取り出す
unsigned int ones = bcd & 0x0F; // 下位4ビットを取り出す
return tens * 10 + ones;
}
int main(void) {
unsigned int value = 45;
// 10進数をBCDに変換
unsigned char bcd = dec_to_packed_bcd(value);
// BCDを10進数に戻す
unsigned int restored = packed_bcd_to_dec(bcd);
// 結果を表示
printf("元の10進数 : %u\n", value);
printf("パックドBCD(16進): 0x%02X\n", bcd);
printf("復元した10進数 : %u\n", restored);
return 0;
}想定される実行結果は次のようになります。
元の10進数 : 45
パックドBCD(16進): 0x45
復元した10進数 : 45このサンプルでは、「10の位を上位4ビット」「1の位を下位4ビット」に詰めることで、パックドBCDを作っています。
逆に、ビット演算で4ビットずつ取り出せば、10進整数へ戻すことができます。
まとめ
BCD(二進化十進数)表現は、10進数の各桁を4ビットずつの2進数で表す方式で、通常の2進数とは目的も意味も異なります。
ビット効率は良くありませんが、その分桁どおりに処理でき、金額や表示などで誤差なく扱えるという大きな利点があります。
電卓や金融システム、組み込み機器など、いまでも実用されている重要な表現方式です。
BCDの仕組みを理解しておくと、2進数と10進数の橋渡しとなる概念がよりクリアになり、低レベルなデータ表現への理解が一段深まります。