C言語の再帰関数は、アルゴリズムを「自分自身を呼び出す関数」として表現する強力なテクニックです。
本記事では、再帰の仕組みを図解と具体的なコード例で丁寧に解説します。
階乗やフィボナッチなどの基本問題から、実務での活用、そして落とし穴までを一通り押さえることで、再帰関数を安全かつ効果的に扱えるようになることを目指します。
C言語の再帰関数とは何か
再帰関数とは
再帰関数(recursive function)とは、自分自身を呼び出す関数のことです。
C言語では、通常の関数定義とまったく同じ書き方で定義できますが、関数の本体の中で、その関数の名前を使って再び呼び出すように記述します。
ポイントは2つあります。
- ベースケース(再帰の終了条件)を必ず用意すること
- 再帰ステップ(自分自身を呼び出す部分)で、ベースケースに近づけるように処理すること
例えば、n!(nの階乗)は次のように定義できます。
- 数学的な定義
- 0! = 1
- n! = n × (n – 1)! (n ≥ 1 のとき)
この定義自体がすでに再帰的です。
そのままC言語の関数にすると、再帰関数になります。
再帰関数のごく単純なイメージ
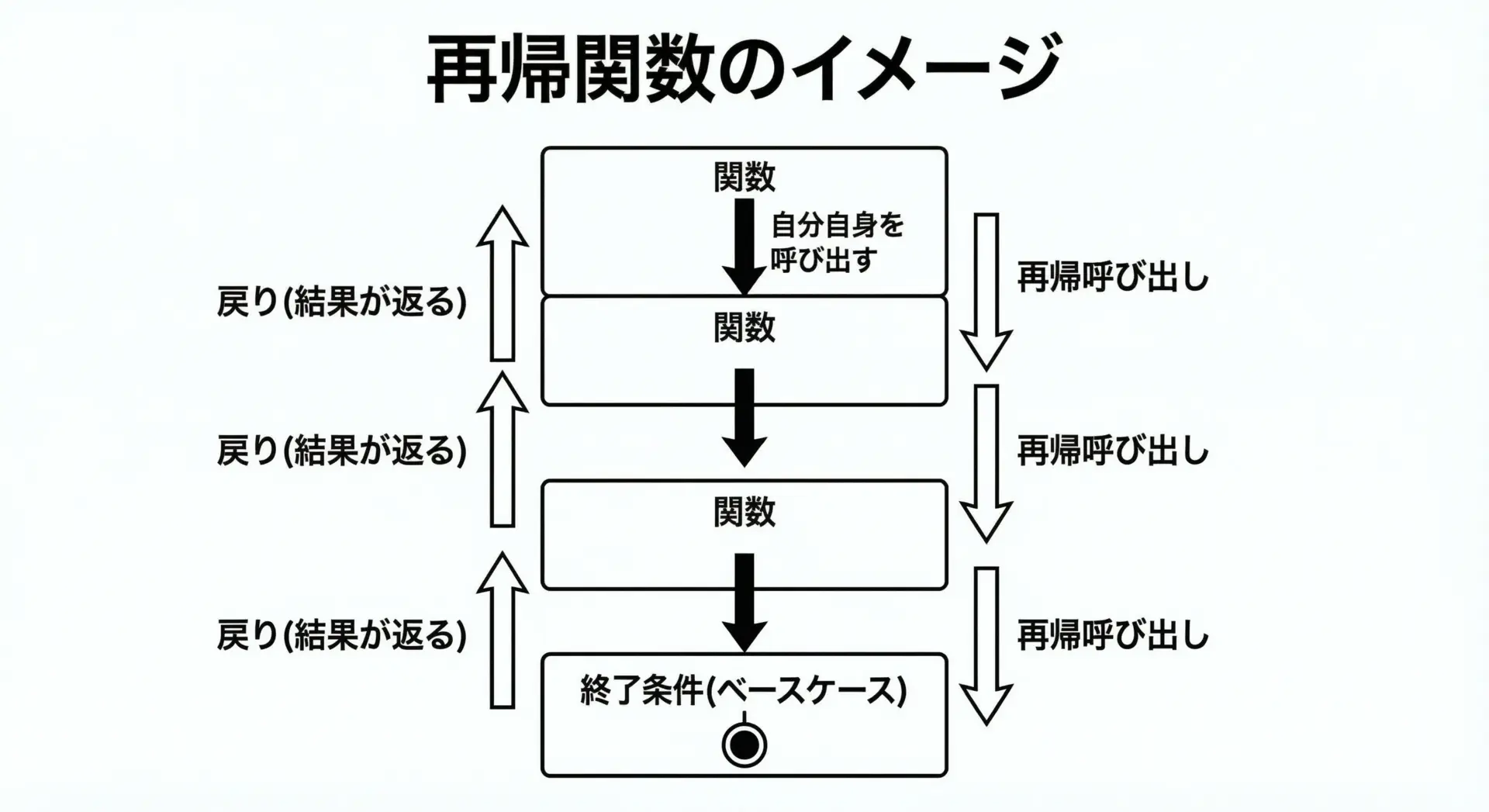
この図のように、再帰関数は同じ処理を、問題を少しずつ小さくしながら何度も呼び出し、最後にベースケースに到達したところで戻りながら結果を組み立てていきます。
再帰関数とループ(for・while)の違い
C言語ではfor文やwhile文を使って繰り返し処理が書けますが、再帰もまた「繰り返し」の一種です。
多くの処理は、ループでも再帰でも書き換えることができます。
違いを直感的に押さえるために、簡単な比較表を見てみます。
| 観点 | ループ(for・while) | 再帰関数 |
|---|---|---|
| 記述スタイル | 変数を更新しながら繰り返す | 関数を何度も呼び出す |
| 状態の保持 | ループ変数・配列インデックスなど | 関数呼び出しスタック(ローカル変数・引数) |
| 理解のしやすさ | 手続き的に追いやすい | 抽象的だが数学的定義に近い |
| メモリ使用 | 一般に少ない | 呼び出しが深いほどスタック消費 |
| 向いているケース | 単純な繰り返し・大量データ処理 | 再帰的構造(ツリー・分割統治など) |
ループは「1つの関数の中で変数を変えながら繰り返す」のに対し、再帰は「関数の呼び出しを積み重ねて繰り返す」イメージです。
C言語で再帰関数を使うメリット・デメリット
メリット
C言語でも、再帰を使うと次のようなメリットがあります。
- コードが数学的な定義に近くなり、アルゴリズムの意図が明確になる
例えば、階乗やフィボナッチ、二分探索、分割統治アルゴリズムなどは、再帰で書くと非常に自然な形になります。 - 木構造(Tree)や再帰的な構造をたどる処理が書きやすい
ファイルシステムの走査、構文木の処理、ゲームAIの探索などは、再帰との相性がよいです。 - some分割して考えるため、問題を小さな部分問題に分けて考える習慣が身につくことも利点です。
デメリット
一方で、C言語で再帰を使うときには次のようなデメリットや注意点があります。
- スタックメモリを多く消費しやすい
呼び出しが深くなるとスタックオーバーフローを起こす危険があります。 - 処理オーバーヘッド
関数呼び出しにはオーバーヘッドがあるため、単純な繰り返し処理ではループの方が高速なことが多いです。 - 終了条件(ベースケース)を間違えると無限再帰になりやすい
ループでいう「無限ループ」と同じく、バグが致命的になりやすいです。 - Cコンパイラは、関数の最適化(特に末尾再帰最適化)を積極的には行わない場合も多く、パフォーマンス面で不利になることがあります。
C言語の再帰関数の仕組みを図解で理解
関数呼び出しスタックの基本
再帰を理解するうえで避けて通れないのが関数呼び出しスタック(call stack)です。
関数が呼ばれるたびに、スタックフレームと呼ばれるメモリ領域が積み上がります。
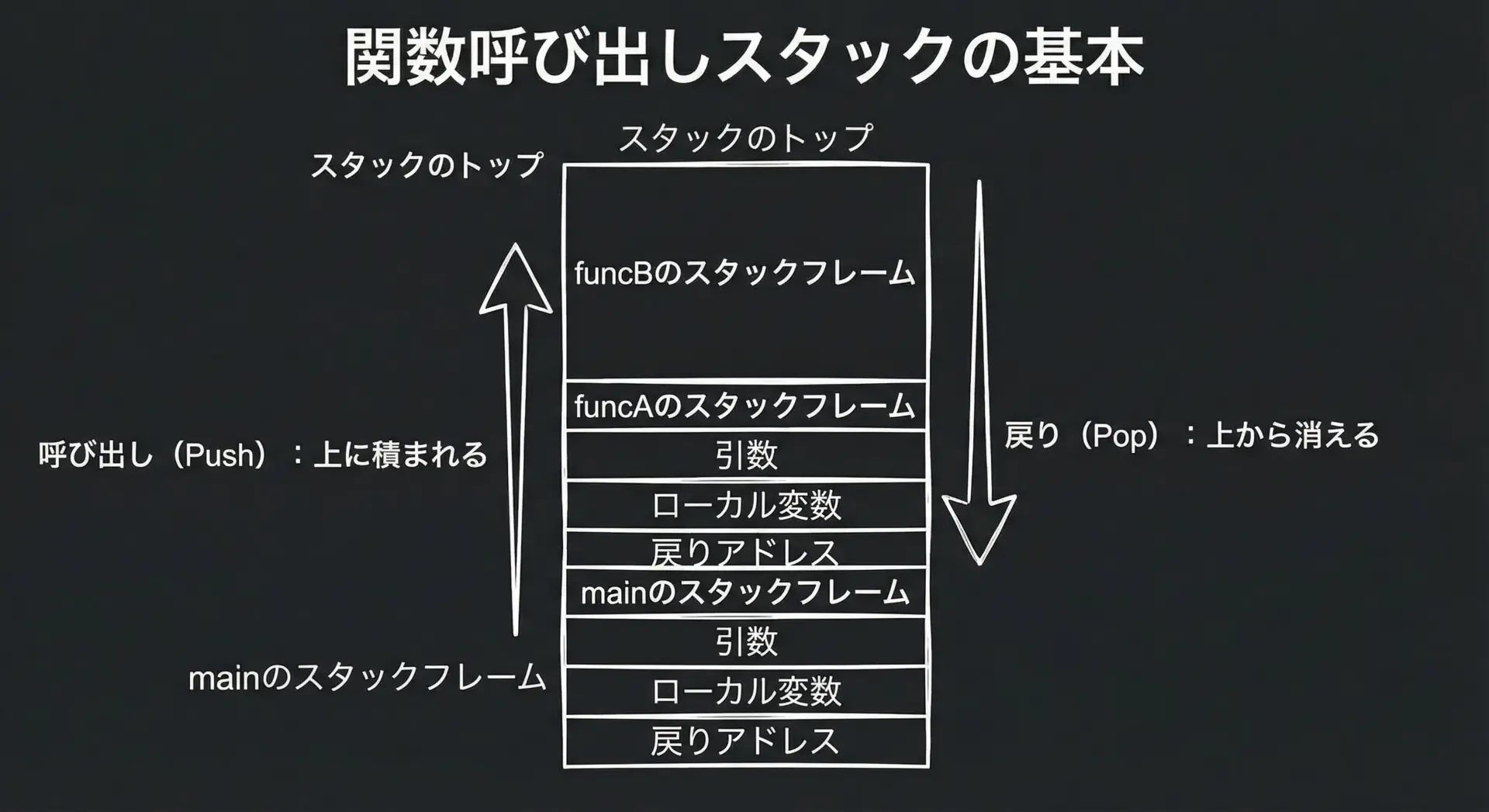
C言語では、関数を呼び出すたびに、次のような情報がスタックに積まれます。
- 呼び出された関数の引数
- その関数のローカル変数
- 戻り先のアドレス(どこに戻ればよいか)
再帰の場合も、毎回新しいスタックフレームが作られるだけで、仕組みは通常の関数呼び出しと同じです。
ただし、自分自身を何度も呼ぶため、同じ関数のスタックフレームが何段も積み重なることになります。
再帰呼び出しの流れを図解で追う
再帰では、関数が呼ばれるたびにスタックが1段増え、ベースケースに到達したあとに、逆順に値が戻っていくという流れになります。
ここでは、簡単な例として「1からnまでの合計を求める再帰関数」を考えます。
#include <stdio.h>
// 1からnまでの合計を求める再帰関数
int sum(int n) {
// ベースケース: nが1なら、合計は1
if (n == 1) {
return 1;
}
// 再帰ステップ:
// sum(n) = n + sum(n - 1) と定義する
return n + sum(n - 1);
}
int main(void) {
int n = 4;
int result = sum(n);
printf("1から%dまでの合計は%dです。\n", n, result);
return 0;
}1から4までの合計は10です。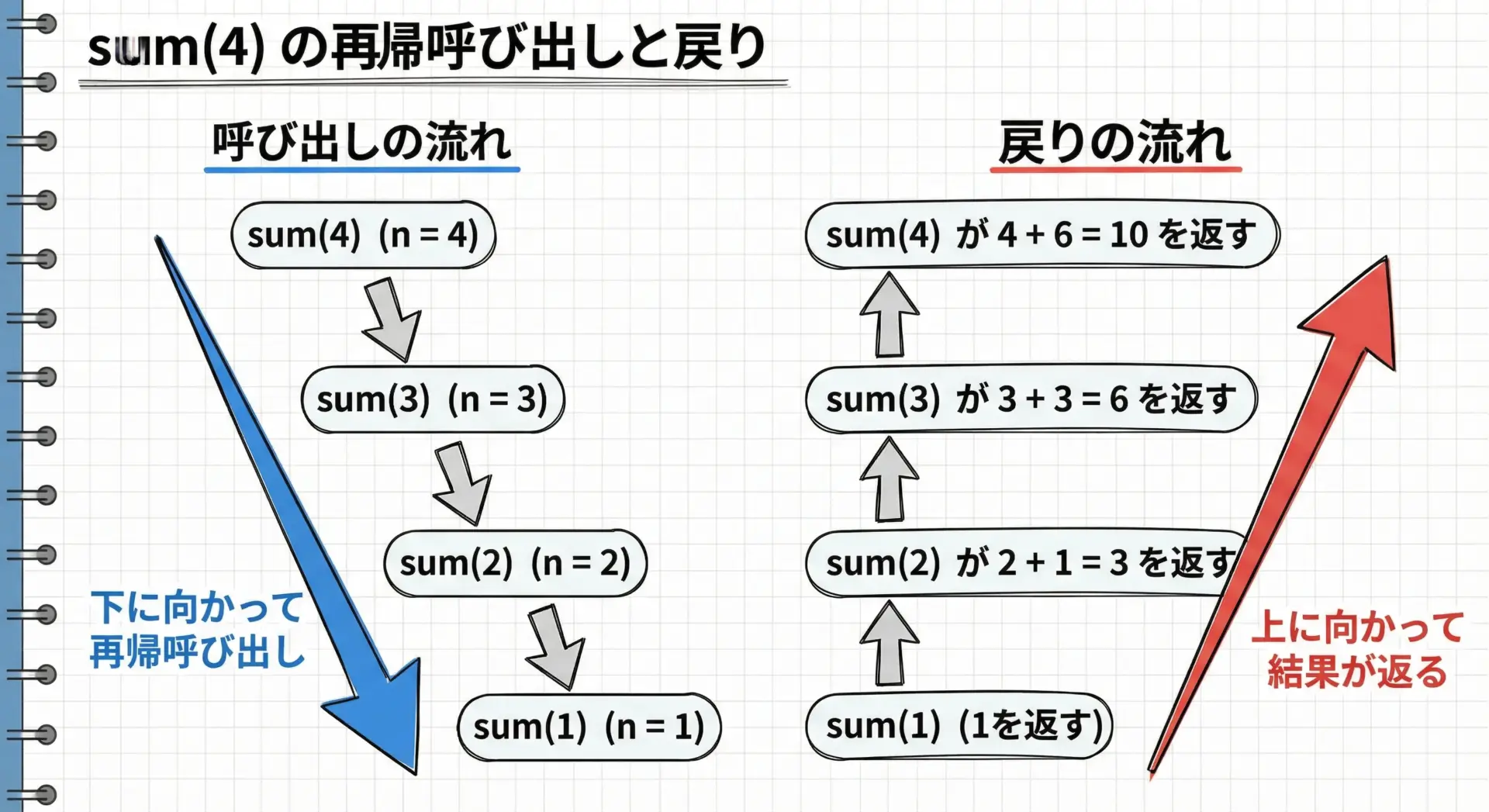
この図のように、再帰では次のような流れで処理が進みます。
- 再帰呼び出しフェーズ
sum(4)がsum(3)を呼び、sum(3)がsum(2)を呼び…というように、ベースケースに到達するまで下に降りていきます。 - 戻りフェーズ
sum(1)が1を返し、それを受け取ったsum(2)が2 + 1を返す…と、上に向かって計算結果が伝播していきます。
ベースケースと再帰ステップの役割
再帰関数を安全に書くうえで、ベースケースと再帰ステップをきちんと分けて考えることが重要です。
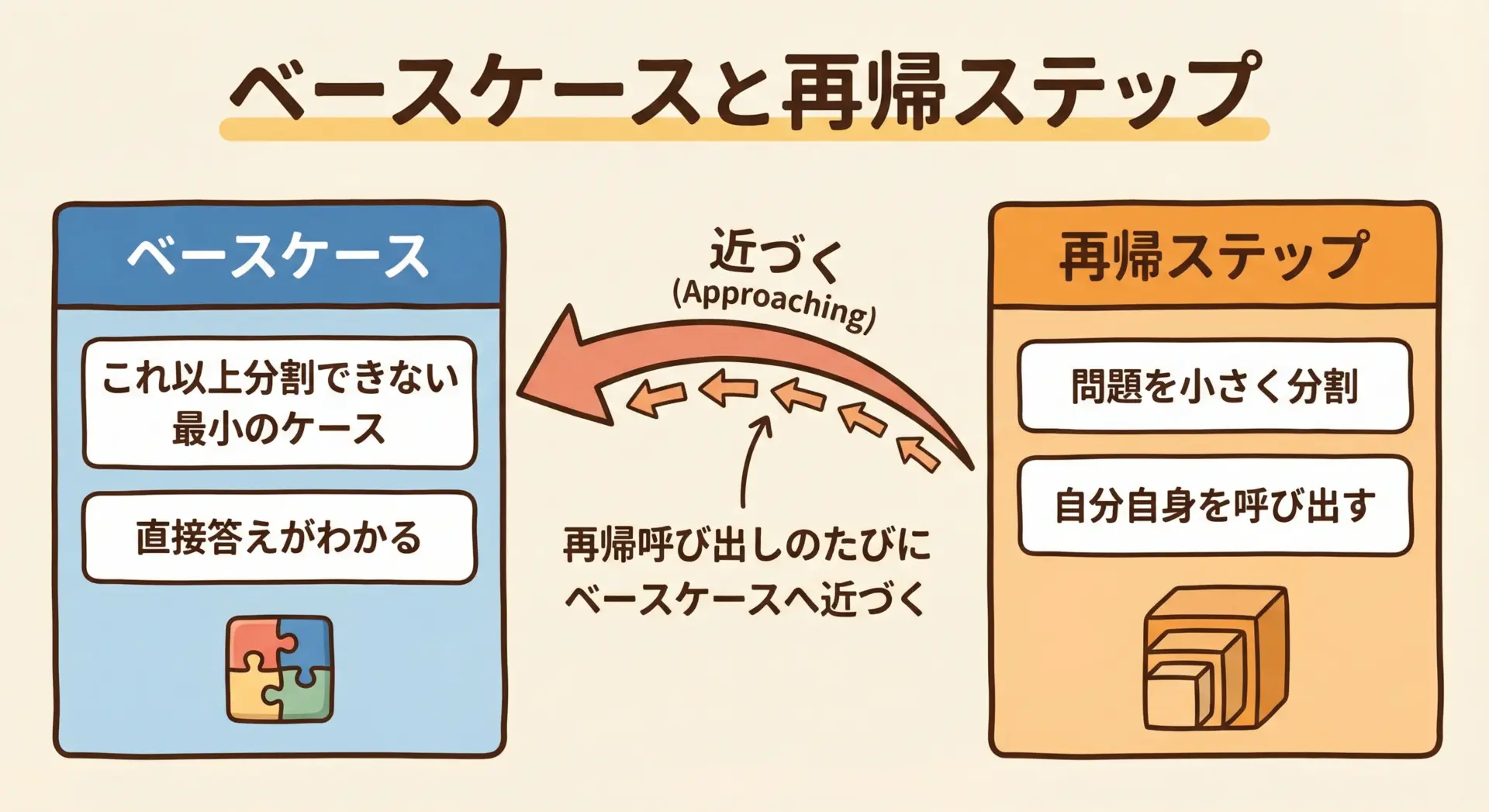
ベースケース(終了条件)
ベースケースは「これ以上分割できない最小の問題」を扱います。
再帰が必ず止まるようにするための条件です。
n == 0やn == 1の場合など、簡単に解答がわかるケース- 配列の長さが0や1の場合など、これ以上分割しても意味がないケース
ベースケースがない、または到達できない条件になっていると、無限再帰になり、プログラムはクラッシュしてしまいます。
再帰ステップ(分割と再帰呼び出し)
再帰ステップでは、元の問題を少し小さな問題に分割して、自分自身を呼び出す処理を書きます。
そして、必ずベースケースに近づくように変化させることが重要です。
例えば、sum(n)の例では以下のようになります。
- ベースケース:
n == 1→ 1を返す - 再帰ステップ:
sum(n) = n + sum(n - 1)
ここでnが1ずつ減ることで、最終的にn == 1になり、ベースケースに到達します。
C言語の再帰関数の基本例題
階乗計算
階乗は再帰の代表的な例です。
n!は次のように定義されます。
- 0! = 1 (ベースケース)
- n! = n × (n – 1)! (n ≥ 1 のときの再帰ステップ)
再帰で書く階乗関数
#include <stdio.h>
// 再帰を使って階乗を計算する関数
unsigned long long factorial(unsigned int n) {
// ベースケース: 0! は 1 と定義する
if (n == 0) {
return 1;
}
// 再帰ステップ:
// n! = n * (n - 1)! という数学的定義をそのまま使う
return n * factorial(n - 1);
}
int main(void) {
unsigned int n = 5;
unsigned long long result = factorial(n);
printf("%u! = %llu\n", n, result);
return 0;
}5! = 120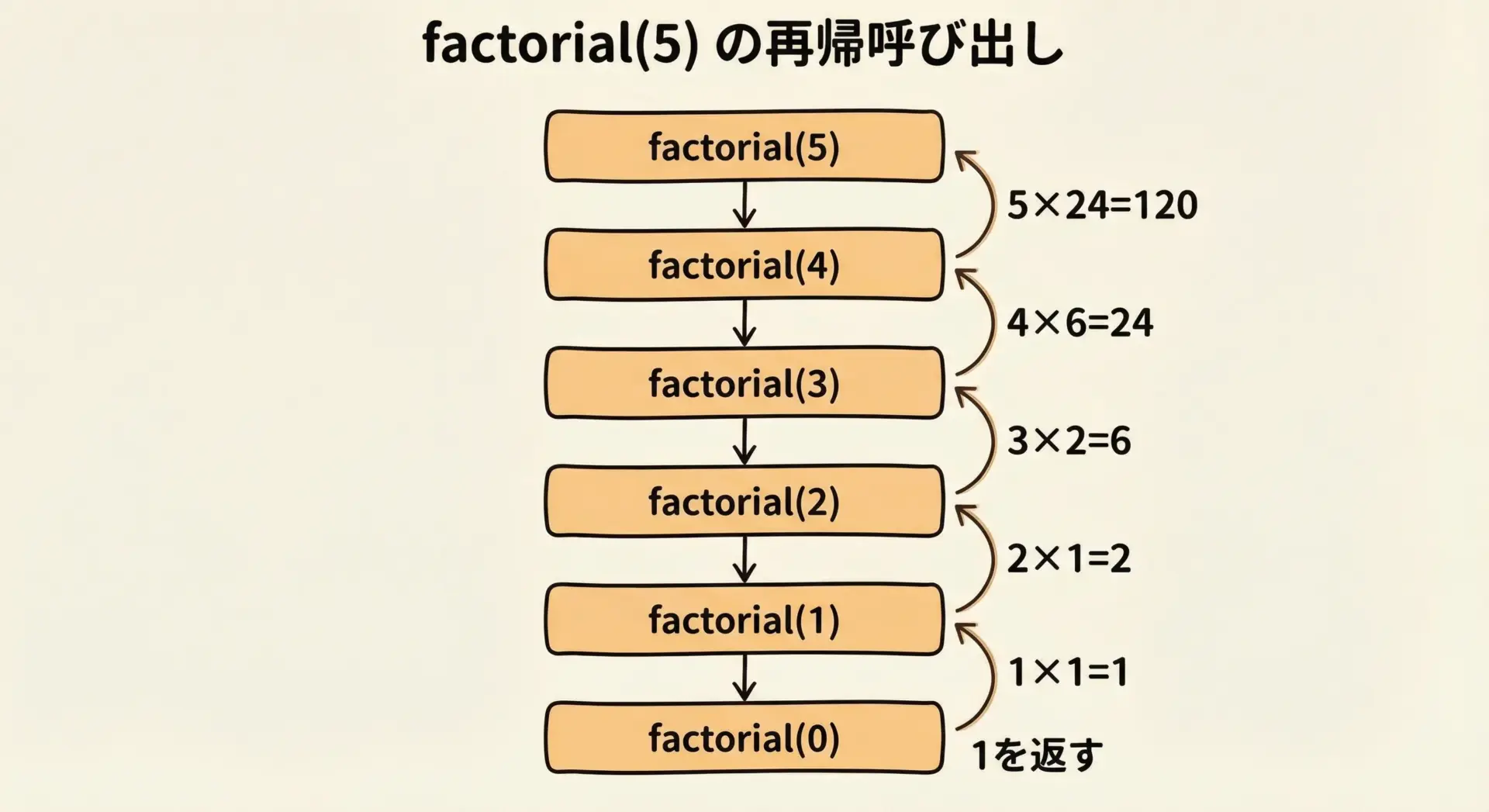
このように、階乗関数は数学的定義をそのままコードに落とし込めるきれいな再帰の例です。
ただし、大きなnではスタックの深さやオーバーフローに注意する必要があります。
フィボナッチ数列
フィボナッチ数列も再帰の典型例ですが、素直な再帰実装は非常に非効率になるというデメリットもよく知られています。
フィボナッチ数列は次のように定義されます。
- F(0) = 0
- F(1) = 1
- F(n) = F(n – 1) + F(n – 2) (n ≥ 2)
素直な再帰実装
#include <stdio.h>
// 再帰でフィボナッチ数列を求める関数(素直な実装)
unsigned long long fibonacci(unsigned int n) {
// ベースケース: 0番目と1番目は定義通りに返す
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
// 再帰ステップ:
// F(n) = F(n - 1) + F(n - 2)
return fibonacci(n - 1) + fibonacci(n - 2);
}
int main(void) {
unsigned int n = 10;
unsigned long long result = fibonacci(n);
printf("F(%u) = %llu\n", n, result);
return 0;
}F(10) = 55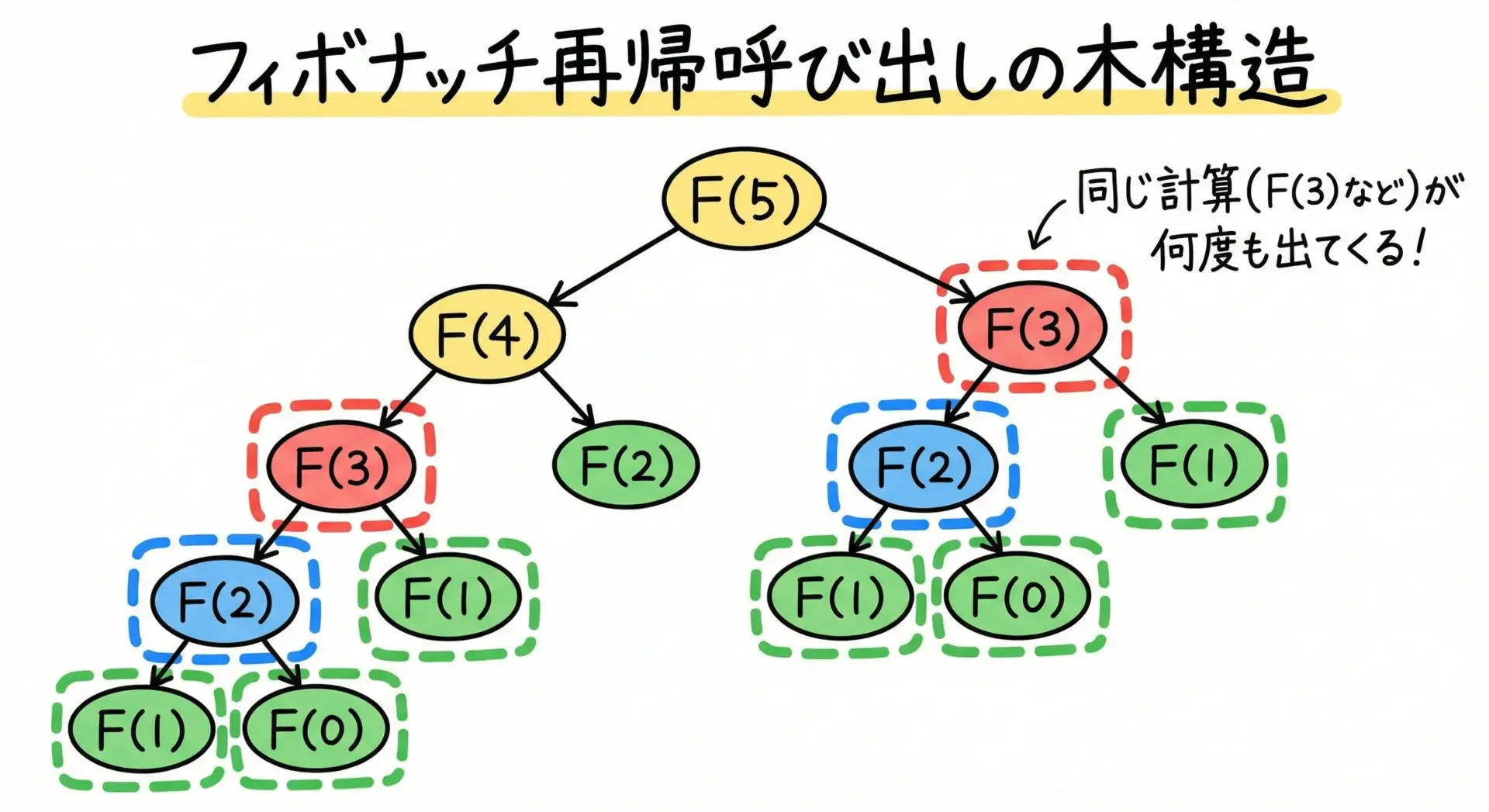
フィボナッチの再帰は、教科書的にはわかりやすい一方で、計算量が爆発的に増えるという問題があります。
同じ値を何度も再計算しているためです。
実務では、メモ化やループによる計算を用いることが多いです。
再帰で書く配列の探索
再帰は線形探索にも使えます。
ここでは、配列の中にある値が存在するかを再帰で調べる例を紹介します。
再帰による線形探索
#include <stdio.h>
#include <stdbool.h>
// 再帰を使った配列の線形探索
// arr: 配列
// size: 配列の要素数
// target: 探したい値
bool linear_search_recursive(const int arr[], int size, int target) {
// ベースケース1: 要素数が0になったら見つからなかった
if (size == 0) {
return false;
}
// ベースケース2: 最後の要素がターゲットなら見つかった
if (arr[size - 1] == target) {
return true;
}
// 再帰ステップ:
// 最後の要素を除いた(サイズを1減らした)配列を探索する
return linear_search_recursive(arr, size - 1, target);
}
int main(void) {
int arr[] = {3, 8, 1, 7, 2};
int size = (int)(sizeof(arr) / sizeof(arr[0]));
int target = 7;
if (linear_search_recursive(arr, size, target)) {
printf("%d は配列の中に見つかりました。\n", target);
} else {
printf("%d は配列の中に見つかりませんでした。\n", target);
}
return 0;
}7 は配列の中に見つかりました。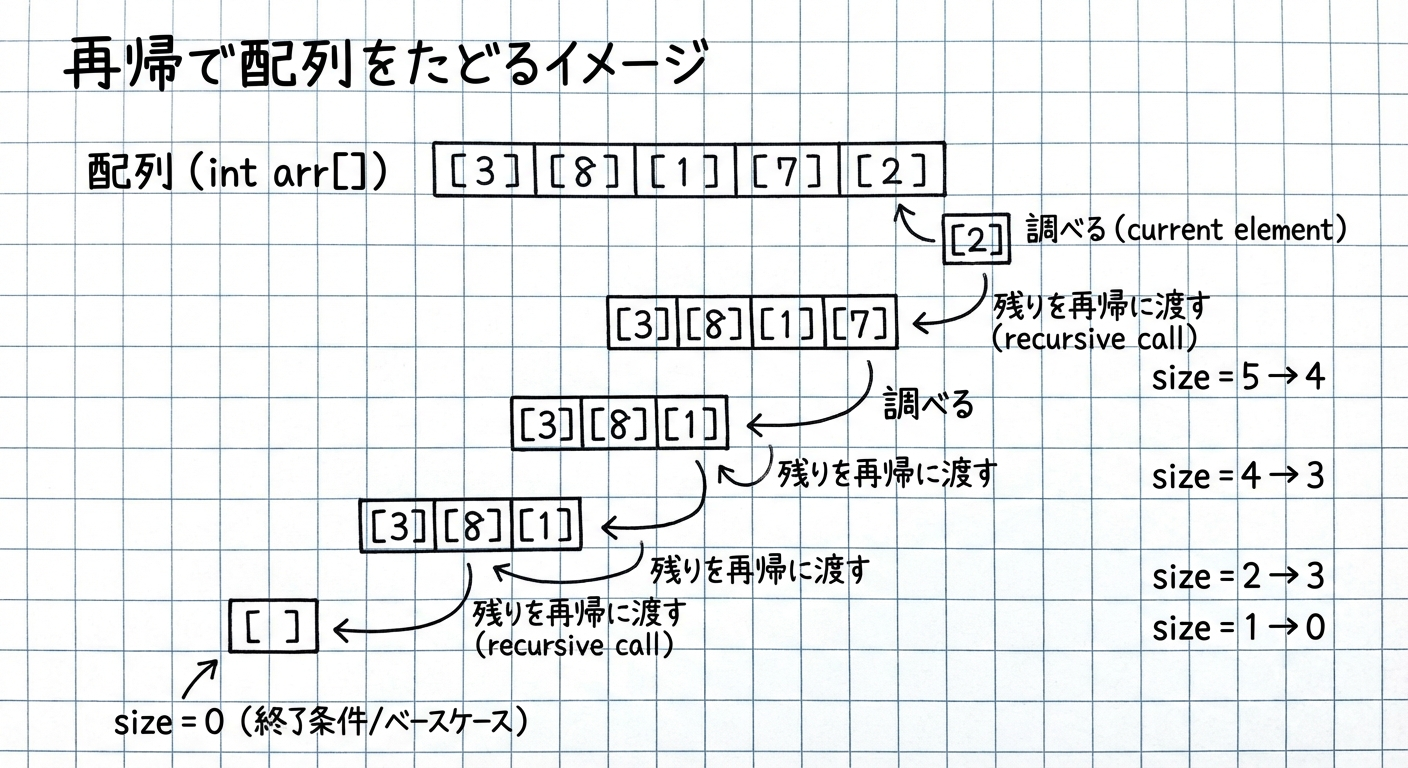
この例では、配列サイズが1ずつ小さくなり、最終的に0になることで、必ずベースケースに到達する構造になっています。
実務での再帰関数の活用例
実務では、再帰は特に再帰的なデータ構造を扱う場面で活躍します。
例えば、ツリー構造やディレクトリの走査などです。
ここでは、2分木(Binary Tree)のノード数を再帰で数える簡単な例を紹介します。
2分木のノード数を数える再帰関数
#include <stdio.h>
#include <stdlib.h>
// 2分木のノードを表す構造体
typedef struct Node {
int value; // ノードが持つ値
struct Node *left; // 左の子ノードへのポインタ
struct Node *right; // 右の子ノードへのポインタ
} Node;
// 新しいノードを生成する関数
Node* create_node(int value) {
Node *node = (Node*)malloc(sizeof(Node));
if (node == NULL) {
// メモリアロケーションに失敗した場合
perror("malloc");
exit(EXIT_FAILURE);
}
node->value = value;
node->left = NULL;
node->right = NULL;
return node;
}
// 再帰で2分木のノード数を数える関数
int count_nodes(const Node *root) {
// ベースケース: 根がNULLならノードは0個
if (root == NULL) {
return 0;
}
// 再帰ステップ:
// 自分自身(1個) + 左部分木のノード数 + 右部分木のノード数
int left_count = count_nodes(root->left);
int right_count = count_nodes(root->right);
return 1 + left_count + right_count;
}
int main(void) {
// 簡単な木を作成する
// 1
// / \
// 2 3
// /
// 4
Node *root = create_node(1);
root->left = create_node(2);
root->right = create_node(3);
root->right->left = create_node(4);
int total = count_nodes(root);
printf("ノード数は %d 個です。\n", total);
// 本来はfreeでメモリを解放すべき(ここではサンプルの簡略化のため割愛)
return 0;
}ノード数は 4 個です。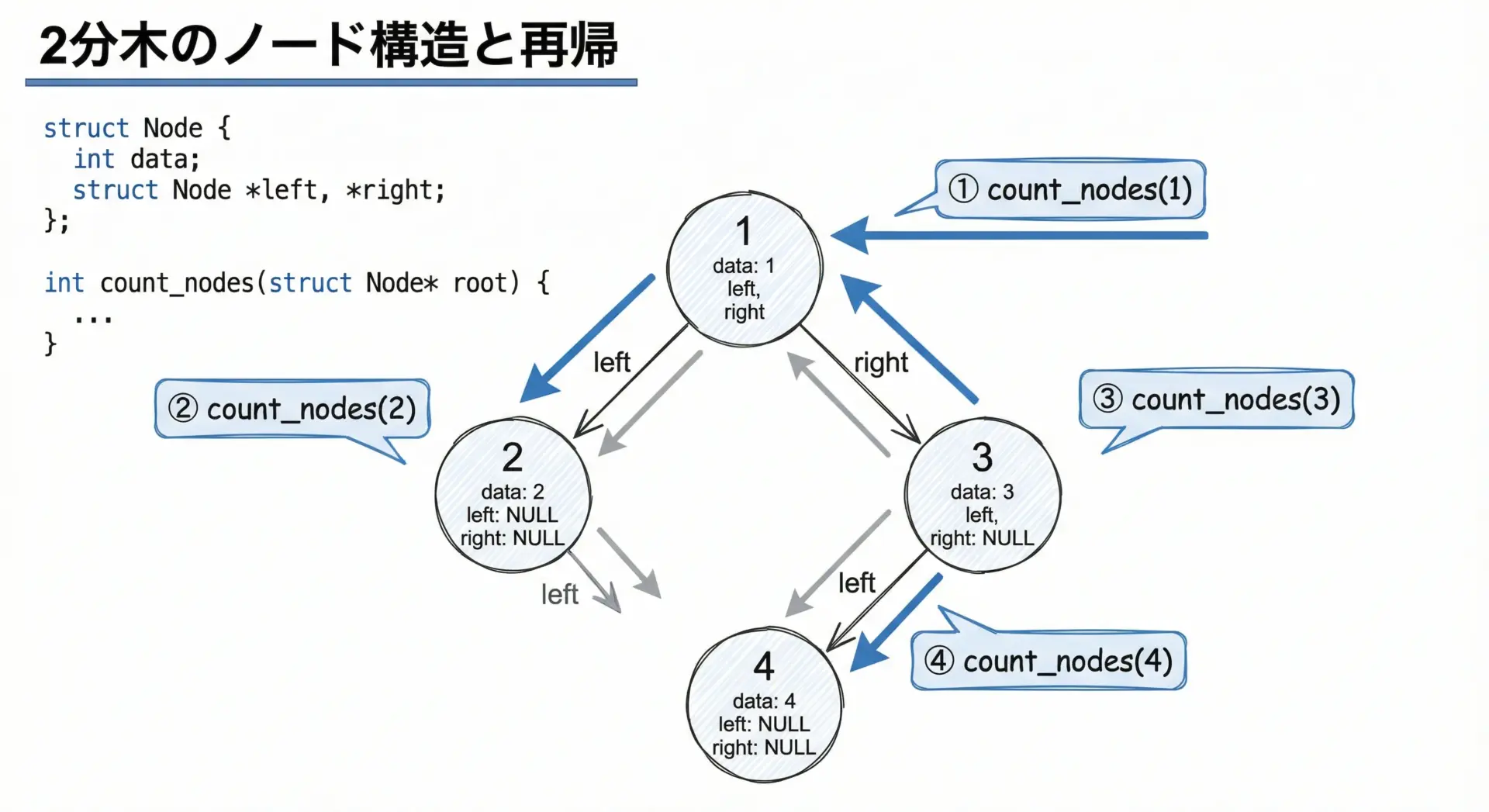
このような木構造処理では、「木全体を処理する」問題を「左部分木」「右部分木」に分割できるため、再帰が非常に自然です。
実務でも、構文木の走査やJSONの解析など、入れ子構造を扱う処理に再帰がよく使われます。
C言語の再帰関数の落とし穴と注意点
無限再帰とスタックオーバーフローの原因
再帰の最大の落とし穴は無限再帰です。
ベースケースに到達しなかったり、条件が間違っていたりすると、関数が延々と自分自身を呼び出し続けます。
その結果、スタックオーバーフローを起こしてプログラムが異常終了します。
典型的な例: ベースケースが間違っている
#include <stdio.h>
// バグのある再帰関数の例(無限再帰になる)
int countdown(int n) {
// 間違ったベースケース: n == 0 のときに止めるべきだが、1としている
if (n == 1) {
return 1;
}
printf("n = %d\n", n);
// nを増やしてしまっているので、ベースケースに近づかない
return countdown(n + 1);
}
int main(void) {
countdown(5); // これを実行すると、ほぼ確実にクラッシュする
return 0;
}このコードでは、nを減らすべきところで増やしてしまっているため、n == 1に決して到達せず、延々と再帰呼び出しが続きます。
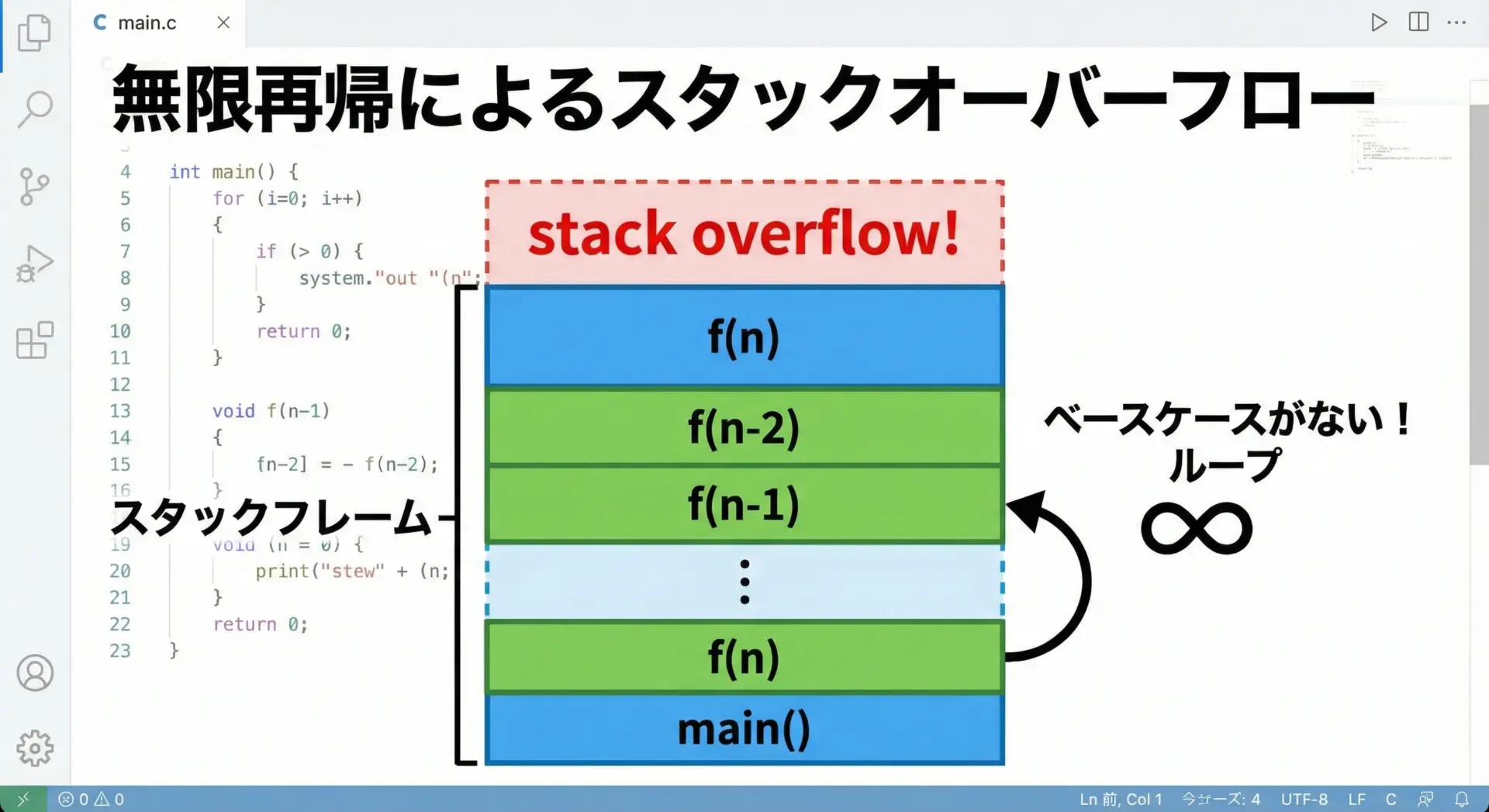
「毎回ベースケースに近づいているか」を必ずチェックするクセをつけることで、この種のバグを減らせます。
再帰関数の引数・戻り値でやりがちなミス
再帰関数では、引数や戻り値の扱いを少しでも間違えると、結果がおかしくなります。
典型的なミス1: 戻り値を返していない
#include <stdio.h>
// バグのある例: 戻り値を返さずに再帰呼び出しだけしている
int sum_bad(int n) {
if (n == 1) {
return 1;
}
// sum_bad(n - 1) を呼び出しているが、
// その戻り値をどこにも使っていない
sum_bad(n - 1);
// 何も意味のない固定値を返している
return n;
}
int main(void) {
int result = sum_bad(4);
printf("結果: %d\n", result);
return 0;
}結果: 4このように、再帰呼び出しの戻り値をきちんと受け取り、それを使って計算した結果を返すことが重要です。
典型的なミス2: 引数の更新を忘れる
#include <stdio.h>
// バグのある例: 引数nを変化させないため、無限再帰になる
int sum_bad2(int n) {
if (n == 1) {
return 1;
}
// sum_bad2(n) と自分と同じ引数で呼び出している
return n + sum_bad2(n); // n - 1 にすべきところ
}
int main(void) {
// 実行すると無限再帰となりクラッシュする
// int result = sum_bad2(4);
// printf("結果: %d\n", result);
return 0;
}再帰ステップの引数が、必ずベースケースに近づくように変化しているかを確認しましょう。
再帰とメモリ使用量
再帰を使うと、呼び出しの深さ分だけスタックフレームが積み上がるため、メモリ使用量が増えます。
C言語ではスタックのサイズは限られているため、深い再帰は危険です。

例えば、次のようなコードで、ループと再帰のスタック使用の違いをイメージできます。
#include <stdio.h>
// ループでカウントダウン
void countdown_loop(int n) {
for (int i = n; i >= 0; --i) {
// ここでは単に表示するだけ
printf("loop i = %d\n", i);
}
}
// 再帰でカウントダウン
void countdown_recursive(int n) {
if (n < 0) {
return;
}
printf("recursive n = %d\n", n);
countdown_recursive(n - 1);
}
int main(void) {
int n = 5;
printf("=== ループ版 ===\n");
countdown_loop(n);
printf("=== 再帰版 ===\n");
countdown_recursive(n);
return 0;
}=== ループ版 ===
loop i = 5
loop i = 4
loop i = 3
loop i = 2
loop i = 1
loop i = 0
=== 再帰版 ===
recursive n = 5
recursive n = 4
recursive n = 3
recursive n = 2
recursive n = 1
recursive n = 0出力は似ていますが、ループ版は常に1つのスタックフレームで処理するのに対して、再帰版はnの深さ分だけフレームが積み重なる点が大きく異なります。
特に、深さが入力サイズに比例して大きくなるアルゴリズムでは、スタックの上限を超える可能性を常に意識する必要があります。
再帰よりループが向いている場面の見分け方
再帰は便利ですが、何でもかんでも再帰で書けばよいわけではありません。
C言語では、次のような観点から「再帰」と「ループ」を使い分けることが重要です。
ループが向いている場面
- 単純な反復処理
例えば、配列全体を単に順番に処理する、カウンタを増やしながら処理するなど。 - 非常に大きな回数の繰り返し
ループの方がスタックを消費せず、オーバーヘッドも小さいため、効率的です。 - 末尾再帰最適化が期待できない処理系
Cコンパイラは末尾再帰を必ずしも最適化してくれないため、深い再帰は危険です。
再帰が向いている場面
- データ構造自体が再帰的になっている場合
木構造やグラフの探索、入れ子になった構造の処理など。 - 分割統治アルゴリズム
クイックソート、マージソート、二分探索など、問題を小さく分割して解くタイプのアルゴリズム。 - 数学的定義が再帰的な問題
階乗、フィボナッチなど。ただし、効率面を考えて実装を工夫する必要があります。
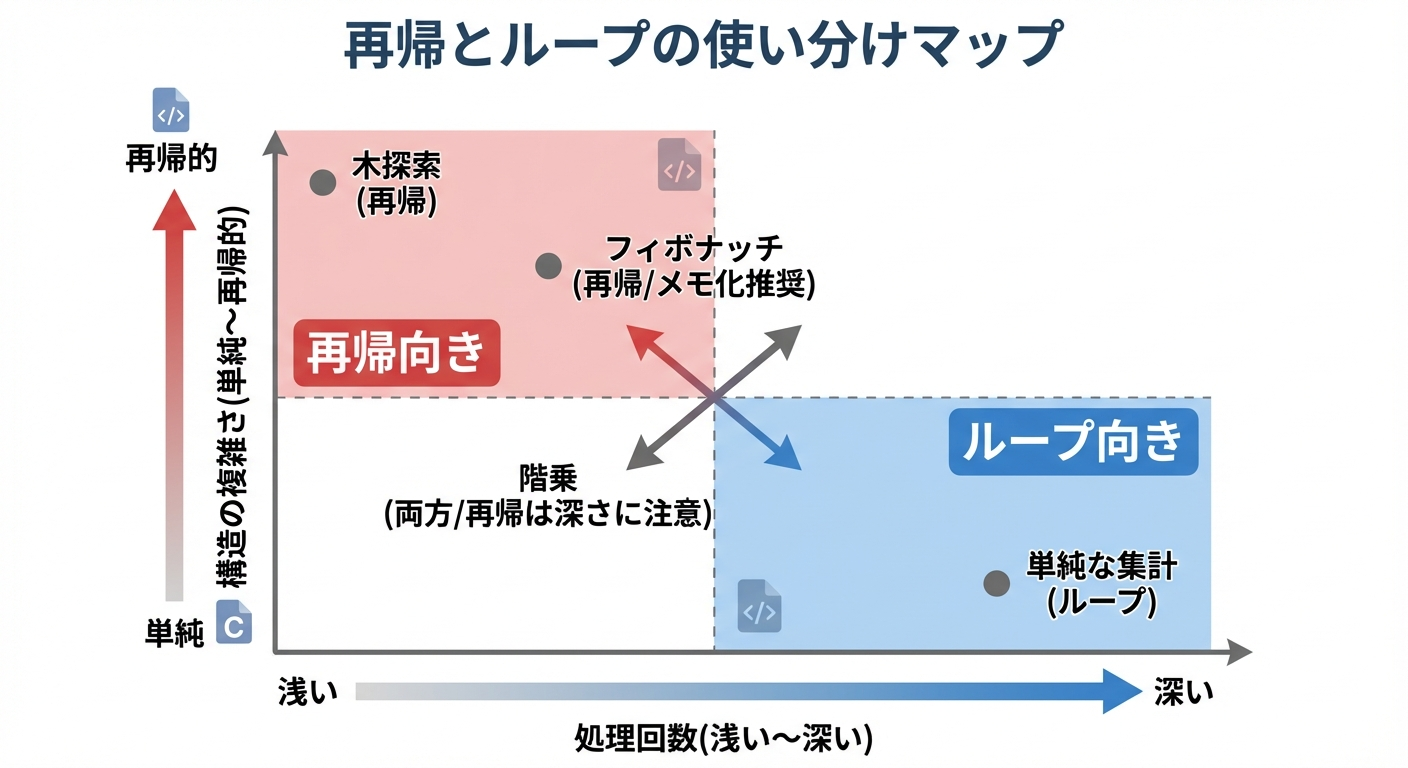
「読みやすさ」と「効率・安全性」のバランスを考えながら、再帰とループを選択するのが実践的です。
まとめ
C言語の再帰関数は、自分自身を呼び出すことで問題を小さく分割しながら解くテクニックです。
階乗やフィボナッチ、配列探索、木構造の走査など、さまざまな場面で登場します。
一方で、ベースケースの不備による無限再帰やスタックオーバーフロー、引数・戻り値の扱いミスといった落とし穴もあります。
本記事で紹介した図解とコード例を参考に、まずは小さな問題から実装とデバッグを繰り返しながら、「ベースケース」と「再帰ステップ」を意識した再帰関数の書き方を身につけていきましょう。