コンピュータで扱う「ランダム」は、一見どれも同じに見えますが、その裏側にはまったく異なる仕組みが存在します。
この記事では、乱数の代表的な2つの種類である疑似乱数と真性乱数について、それぞれの特徴や仕組み、そしてどのような場面で使い分けるべきかを、できるだけ直感的に分かるように解説します。
プログラミングやセキュリティに関わる方はもちろん、「コンピュータのランダムって本当にランダムなの?」と気になっている方にも役立つ内容です。
乱数とは何か
乱数とは、一見すると規則性がなく予測できないように見える数列を指します。
サイコロの目やコイン投げの表裏のような現象は、日常的に目にする乱数の例といえます。
コンピュータの世界でも、乱数はさまざまな用途で使われます。
例えば、ゲームで敵の出現タイミングを変えたり、シミュレーションで多数のパターンを試したり、暗号鍵の生成に利用したりと、その役割は非常に幅広いです。
ここで重要なのは、「予測できなさ」がどの程度求められるかによって、使うべき乱数の種類が変わるという点です。
これを理解するために、まず疑似乱数と真性乱数の違いを整理していきます。

コンピュータは、サイコロや風の揺らぎのような物理現象そのものを直接扱うことが苦手です。
そのため、アルゴリズムで乱数らしさを作り出す方法(疑似乱数)と、物理現象などから不確定さを取り出す方法(真性乱数)の2つが発展してきました。
疑似乱数とは
疑似乱数(pseudo random number)とは、数学的なアルゴリズムによって生成される「見かけ上ランダムな数列」のことです。
「疑似」という言葉が示す通り、本質的には決定論的であり、同じ条件からは同じ乱数列が再現されます。
疑似乱数の基本的な仕組み
疑似乱数では、シード値(seed)と呼ばれる初期値をもとに、乱数生成アルゴリズムを繰り返し適用します。
すると、一見ランダムに見える数列が得られます。

代表的な特徴は次の通りです。
- 決定論的: 同じシード値とアルゴリズムから、必ず同じ乱数列が生成されます。
- 高速: 単純な演算の繰り返しなので、非常に高速に大量の乱数を生成できます。
- 統計的なランダムさ: 長い目で見ると、0〜1の間に均等に散らばるなど、統計的な性質を乱数に近づけることができます。
有名な疑似乱数アルゴリズムには、Mersenne Twisterや線形合同法などがあります。
プログラミング言語に標準で用意されているrand()の多くは、こうした疑似乱数生成器(PRNG: Pseudo Random Number Generator)に基づいています。
疑似乱数のメリット
疑似乱数には、実務的に大きなメリットがあります。
1つ目のメリットは、再現性があることです。
例えば、シミュレーションや機械学習の実験では、「同じ実験条件を再度試したい」という場面が頻繁にあります。
このとき、シード値を固定しておけば、毎回同じ乱数列が得られるため、結果の比較が容易になります。
2つ目は、処理速度の速さです。
ゲーム開発やグラフィックス、モンテカルロ法のように大量の乱数を必要とする場面では、高速に生成できる疑似乱数がほぼ必須です。
3つ目は、実装や利用のしやすさです。
ライブラリとして整備されており、多くの開発環境で簡単に利用できます。
また、アルゴリズムが公開されているため、必要に応じて実装を確認したり、自分で実装したりすることも可能です。
疑似乱数の限界と注意点
一方で、疑似乱数には本質的な限界もあります。
最大の問題は、「完全には予測不可能ではない」ことです。
疑似乱数は数学的な手順で生成されるため、アルゴリズムとシード値が分かれば、将来の乱数列を計算できます。
暗号やセキュリティのように、第三者に予測されてはいけない用途には、そのままでは向きません。
また、乱数列には有限の「周期(period)」がある点も重要です。
ある程度長く乱数を使い続けると、最初の状態に戻り、同じ数列が繰り返されてしまいます。
優れたPRNGは周期が非常に長く実用上問題ないよう設計されていますが、用途によっては周期の長さも選定の条件になります。
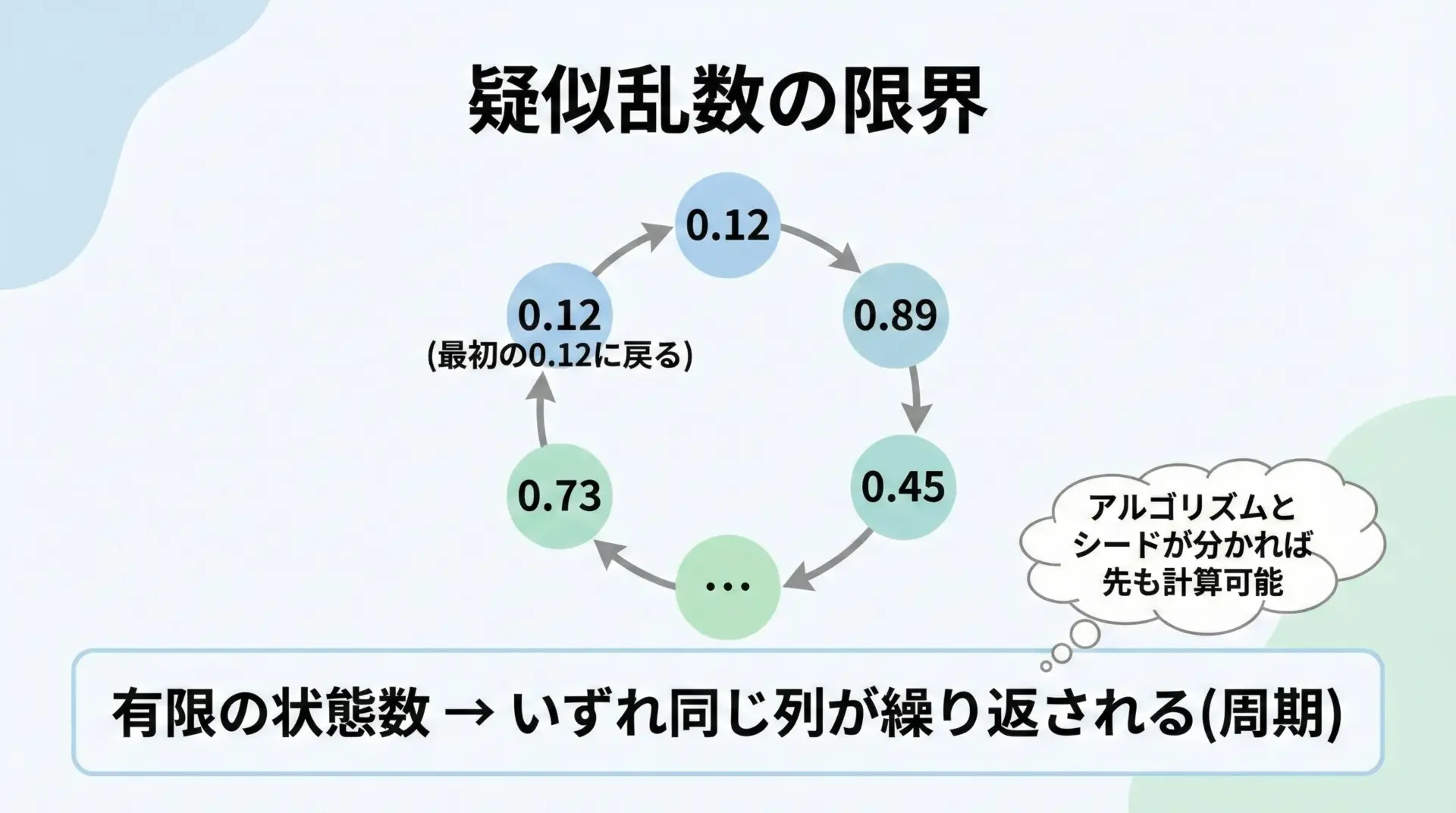
このように、疑似乱数は実用上便利である一方、「本当に予測不能であること」が重要な場面には、そのままでは使えないという点を押さえておく必要があります。
真性乱数とは
真性乱数(true random number)とは、物理現象など、根本的に予測できない要素を利用して生成される乱数です。
英語ではTRNG(True Random Number Generator)と呼ばれます。
真性乱数の基本的な仕組み
真性乱数は、自然界やハードウェアの「ゆらぎ」を利用します。
例えば次のような情報源が使われます。
- 放射性崩壊のタイミング
- 電子回路の熱雑音
- キーボードやマウス操作のタイミング
- ハードディスクのアクセス時間の揺らぎ など
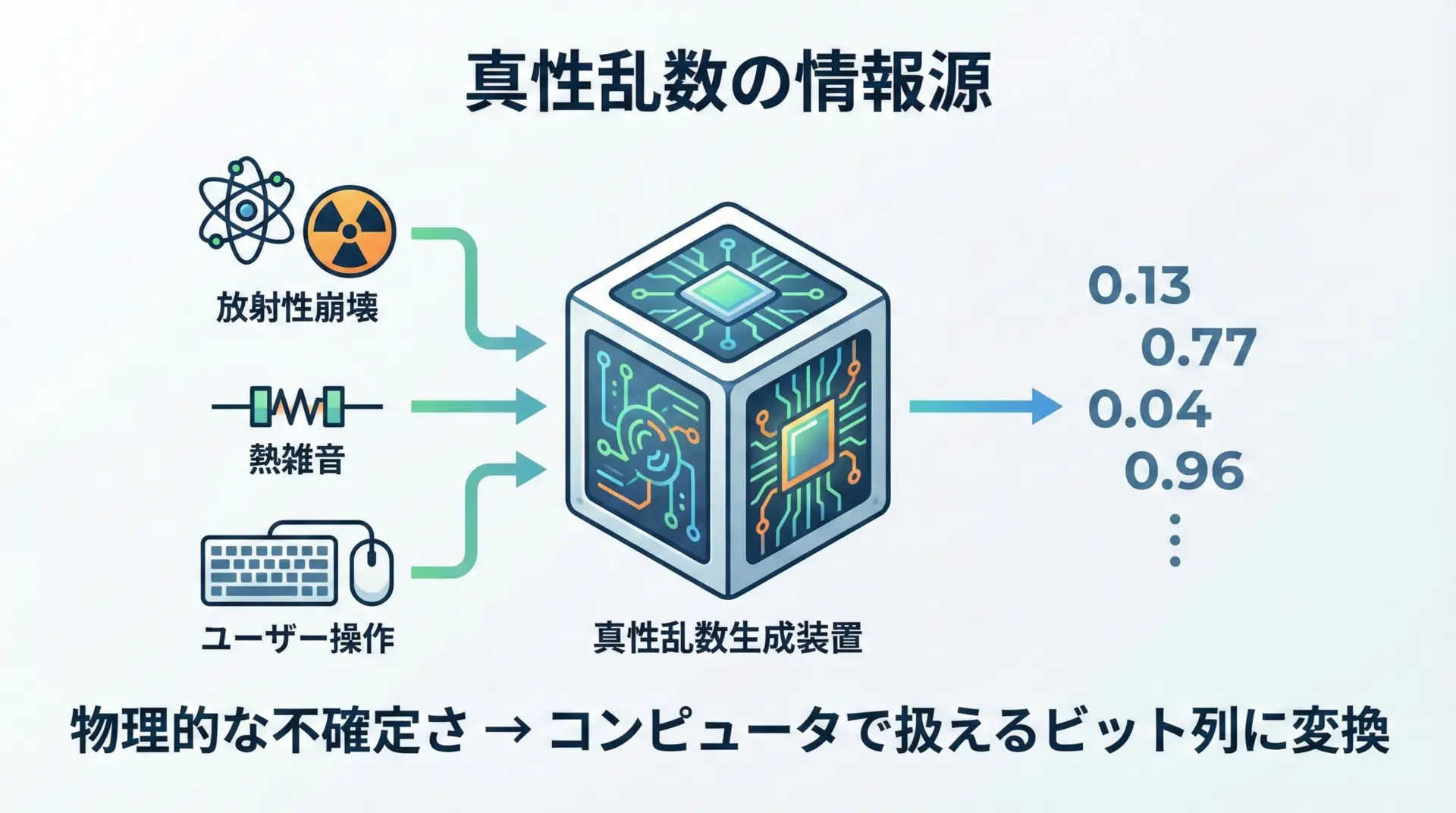
これらの物理現象は、量子力学的な不確定性や多くの要素が絡み合うカオス性などにより、理論的にも完全には予測できないと考えられています。
そのため、第三者が将来の値を推測することが極めて困難であり、セキュリティ用途に適しています。
実際の装置では、物理現象から得られた信号をデジタル化し、その偏り(0と1の出現頻度の差など)を減らすための「ホワイトニング」処理を行った上で、乱数として提供します。
真性乱数の特徴とメリット
真性乱数の最大の特徴は、理論的な「予測不能さ」の高さです。
暗号鍵の生成のように、一度でも予測されると致命的な被害につながるケースでは、この性質がとても重要です。
例えば、SSL/TLS通信やVPN、ハードウェアセキュリティモジュール(HSM)などでは、真性乱数、あるいはそれに準じた高品質な乱数が用いられます。
また、真性乱数はアルゴリズムの周期に縛られないため、「どこまで行ってもパターンが繰り返されない」という意味での安全性もあります。
真性乱数の課題と制約
ただし、真性乱数には実用面での課題も少なくありません。
1つ目は、生成速度の制限です。
物理現象を観測するには時間がかかるため、疑似乱数ほど高速に大量の乱数を生成することは難しい場合があります。
大量の乱数を短時間で必要とするシミュレーションなどには、基本的には不向きです。
2つ目は、ハードウェアや装置のコストです。
放射線源や特殊な回路を用いた乱数生成装置は、一般的なPCには標準搭載されていません。
近年はCPU内に簡易的なハードウェア乱数源を備えたものも増えていますが、それでも用途や品質には限界があります。
3つ目は、品質管理の難しさです。
物理現象を扱うため、環境変化(温度、経年劣化、ノイズ源の変化など)の影響を受けやすく、その結果として偏りや異常が出る可能性があります。
そのため、定期的な統計的テストや監視が必要になります。
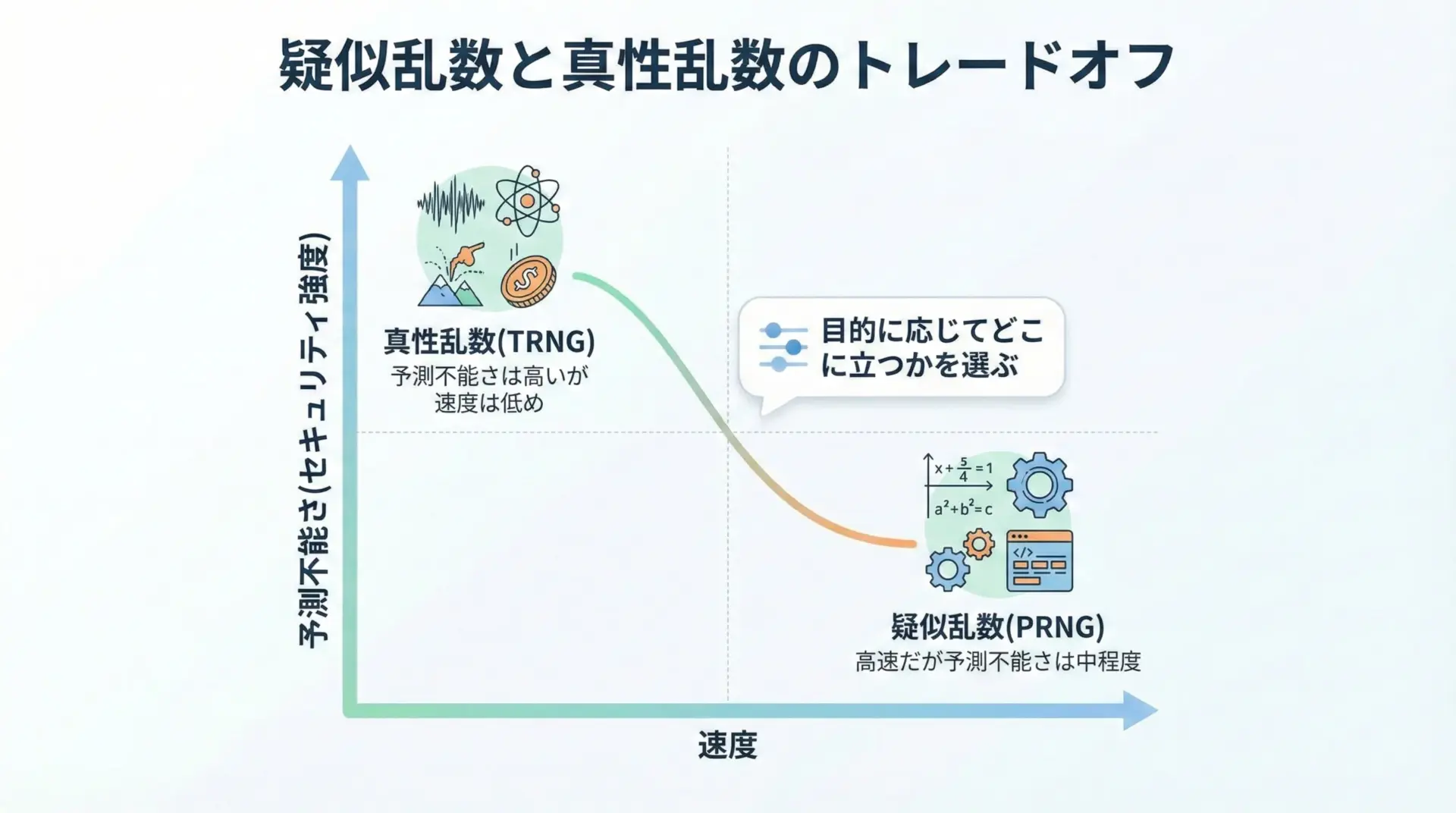
このように、真性乱数はセキュリティ面では非常に魅力的ですが、万能ではなく、コストや速度とのバランスを見て導入する必要があるといえます。
疑似乱数と真性乱数の違い
ここまでの内容を踏まえ、疑似乱数と真性乱数の違いを整理します。
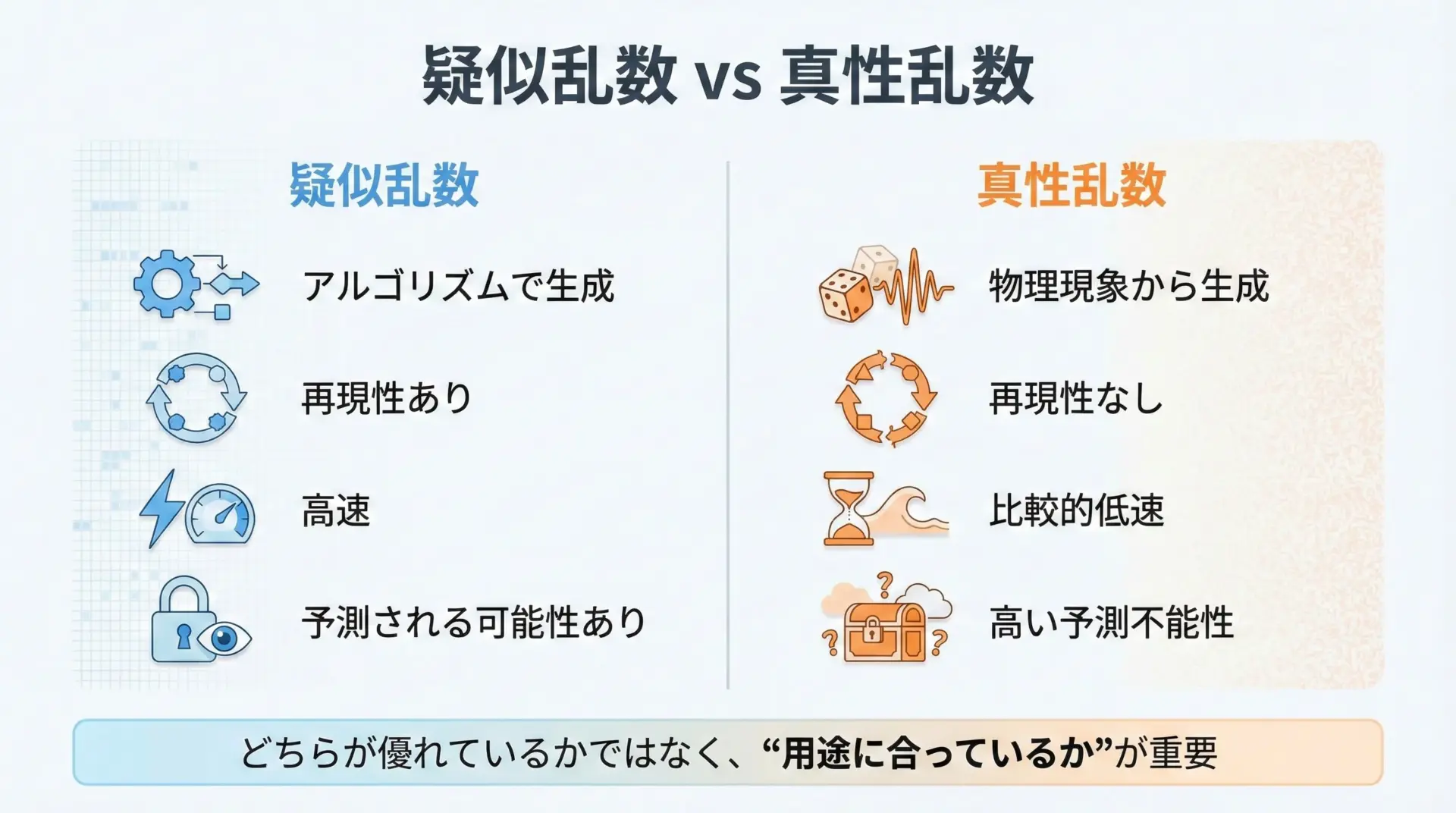
文章としては、次のような対比になります。
生成原理については、疑似乱数が数学的アルゴリズムに依存するのに対し、真性乱数は物理現象に依存します。
この違いが、あらゆる性質の差につながっています。
再現性の面では、疑似乱数は同じシード値から同じ結果が得られるのに対し、真性乱数は基本的に同じ乱数列を再現することができません。
これは、検証やデバッグのしやすさという点で大きな違いになります。
速度とスケーラビリティでは、疑似乱数に軍配が上がります。
アルゴリズムのみで生成できるため、非常に高速で、大量の乱数を求める用途に向いています。
一方、真性乱数は物理現象を観測するという性質上、速度やスループットには限界があります。
セキュリティの観点では、真性乱数が有利です。
疑似乱数はアルゴリズムとシード推定のリスクがあるため、暗号用途には「暗号論的擬似乱数生成器(CSPRNG)」と呼ばれる、特別に設計された疑似乱数を利用するのが一般的です。
このCSPRNGも、内部的には真性乱数などから得たエントロピーをシードとして使うことが多く、疑似乱数と真性乱数が組み合わされて運用されているケースがほとんどです。
用途別の使い分け
では、実際の開発や運用では、どのように疑似乱数と真性乱数を使い分ければよいのでしょうか。
代表的なケースごとに整理します。
ゲーム開発・シミュレーション
ゲームにおける敵の行動パターンやアイテムドロップ、物理シミュレーションなどでは、統計的にランダムであれば十分であり、再現性も重要です。
このような場面では、次のような方針が一般的です。
- 基本は高速な疑似乱数(PRNG)を使用
- テストやデバッグ用途ではシード値を固定して、挙動を再現可能にする
- 本番では、起動時に現在時刻などをもとにシードを設定し、プレイヤーからは予測しにくくする
セキュリティ上の深刻な影響がない限り、真性乱数を使う必要性は高くありません。
統計解析・モンテカルロ法
統計解析や金融工学などで用いられるモンテカルロ法では、膨大な数の乱数を用いて確率的な現象を近似します。
この場合も、高速性と再現性が最優先であり、疑似乱数が適しています。
むしろ、真性乱数のように「完全に予測不能」であることは、再現性の観点からデメリットになり得ます。
ただし、乱数の品質(分布の均一性や長い周期など)は結果に大きな影響を与えるため、品質が検証された高品質なPRNGを選ぶことが重要です。
暗号・セキュリティ
パスワード生成、暗号鍵の生成、トークンの発行など、第三者に推測されてはいけない用途では、乱数の扱いが特に重要になります。
ここでは、次の考え方が一般的です。
- 真性乱数(あるいはハードウェア乱数源)を、エントロピー源として利用
- そのエントロピーを暗号論的擬似乱数生成器(CSPRNG)に投入し、大量の乱数を生成
- 直接PRNG(一般的な
rand()など)を鍵生成に使うことは避ける
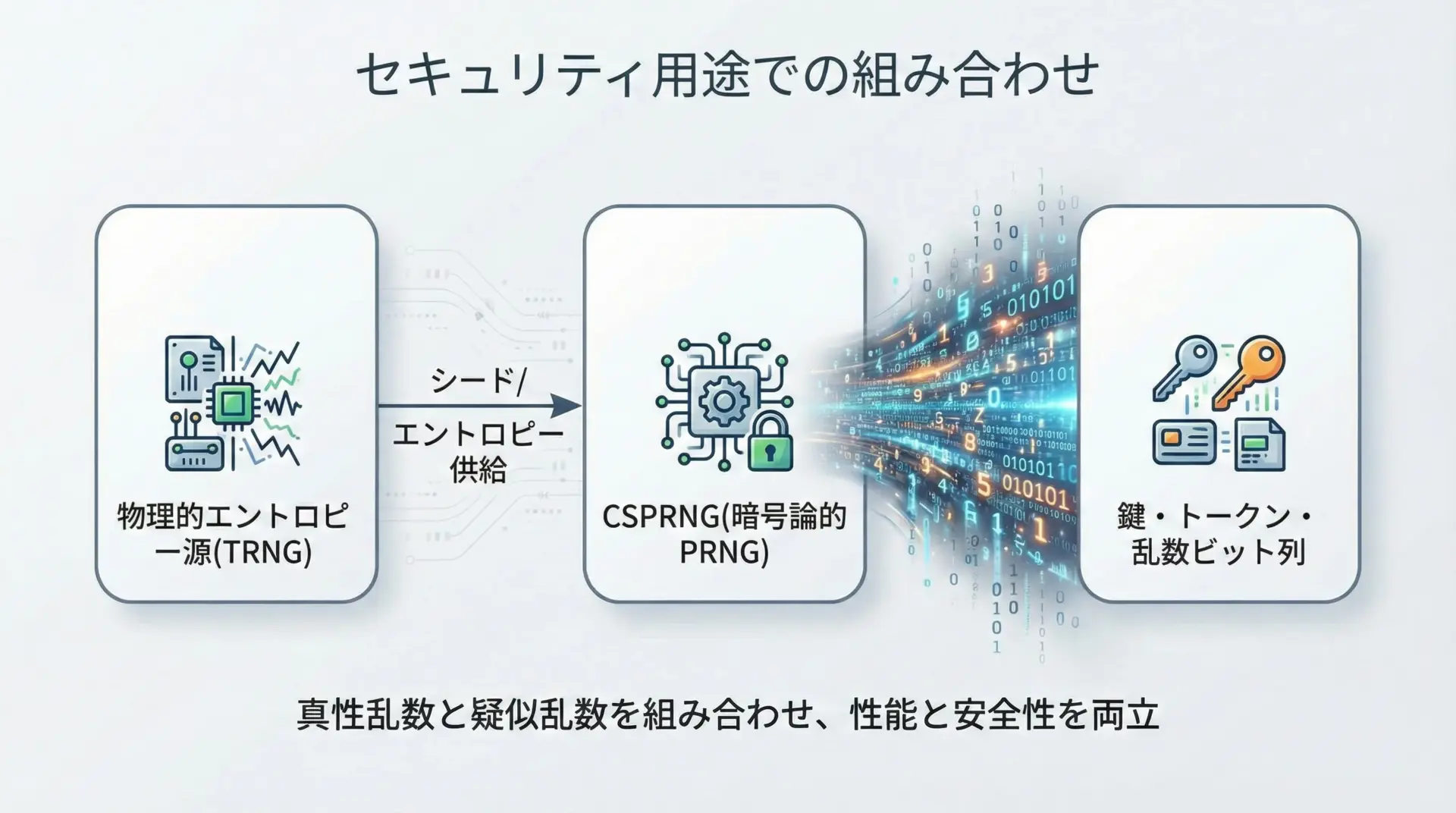
このように、セキュリティの世界では、疑似乱数と真性乱数は対立する存在ではなく、むしろ補い合う関係になっています。
一般的なプログラミング
Webアプリケーションでのトークン生成や、一時的な識別子の生成など、「そこまで厳密な暗号強度は不要だが、ある程度の予測不能さは欲しい」という場面も多く存在します。
このような場合は、言語やフレームワークが提供する「セキュアな乱数API」を利用するのが基本です。
例えば次のような関数は、多くの場合、内部でCSPRNGやOSの提供する安全な乱数源を利用しています。
/dev/urandom(Unix系OS)CryptGenRandom、BCryptGenRandom(Windows)java.security.SecureRandom(Java)crypto.randomBytes()(Node.js)random.SystemRandom(Python) など
重要なのは、用途に応じて「通常のPRNG」と「セキュアな乱数API」を使い分ける意識を持つことです。
乱数を選ぶときの考え方
最後に、実務で乱数の種類を選ぶ際の考え方をまとめます。
ポイントは「何を優先したいのか」を明確にすることです。
1つ目の軸は、セキュリティ(予測不能さ)がどこまで重要かです。
少しでもセキュリティに関わる要素がある場合は、通常の疑似乱数ではなく、CSPRNGやOSのセキュア乱数APIを使うことを検討すべきです。
2つ目の軸は、再現性が必要かどうかです。
シミュレーションやテストでは再現性が重要になるため、シード制御がしやすいPRNGが向いています。
この場合、セキュリティよりも統計的性質や速度を重視して選びます。
3つ目の軸は、生成量と速度です。
大量かつ高速に乱数を必要とするなら、基本はPRNG、セキュア用途では「TRNGでシードしたCSPRNG」といった構成が現実的です。
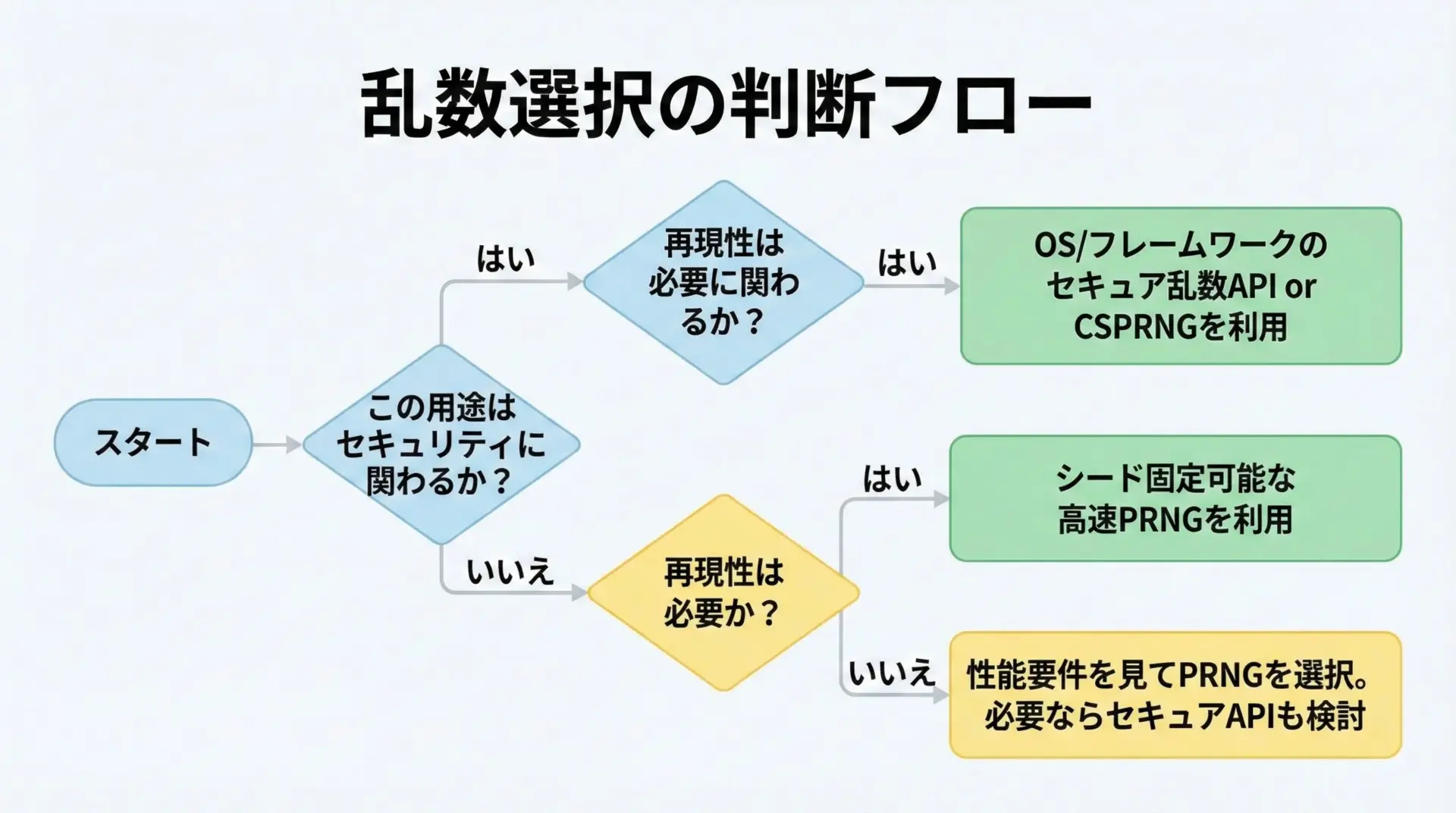
このような観点を押さえておけば、「乱数の種類が多くてよく分からない」という状況から一歩抜け出し、目的に合わせて乱数の仕組みを選べるようになるはずです。
まとめ
この記事では、疑似乱数と真性乱数という2つの乱数の種類について、その仕組みと特徴、そして用途に応じた使い分けの考え方を解説しました。
疑似乱数は、アルゴリズムとシード値から決定論的に生成される、再現性と高速性に優れた乱数です。
ゲーム、シミュレーション、統計解析など、大量の乱数を扱い、かつ再現が重要な場面で大きな力を発揮します。
真性乱数は、物理現象由来の不確定さを利用した、高い予測不能性を持つ乱数です。
暗号鍵の生成や高度なセキュリティが求められる用途で、「第三者に予測されないこと」を保証するための重要な基盤となります。
実際のシステムでは、真性乱数で得たエントロピーをもとにCSPRNGを動かすなど、両者を組み合わせて使うことが主流です。
乱数を選ぶときには、セキュリティの重要度、再現性の必要性、生成速度と量といった観点から、自分の用途に合った仕組みを選ぶことが大切です。
コンピュータの「ランダム」は万能ではありませんが、その仕組みと特徴を理解して適切に使い分けることで、安全で信頼性の高いシステムやアプリケーションを設計することができます。
今回紹介した考え方を踏まえ、次に乱数を使うときには、裏側でどのような仕組みが動いているのかを意識してみてください。