正の無限大・負の無限大の扱い方を高校数学レベルで解説

2025年10月25日2026年1月14日

その他

高校数学では、極限やグラフを考えるときに正の無限大や負の無限大が何度も登場します。

しかし、実数とは少し違う特別な存在なので、正しくイメージできていないと計算でつまずきやすくなります。

この記事では高校数学レベルで分かる範囲にしぼって、正の無限大・負の無限大の意味や計算での扱い方を丁寧に解説します。

目次 [ close ]

正の無限大・負の無限大とは何か

無限大は「数」ではないという前提

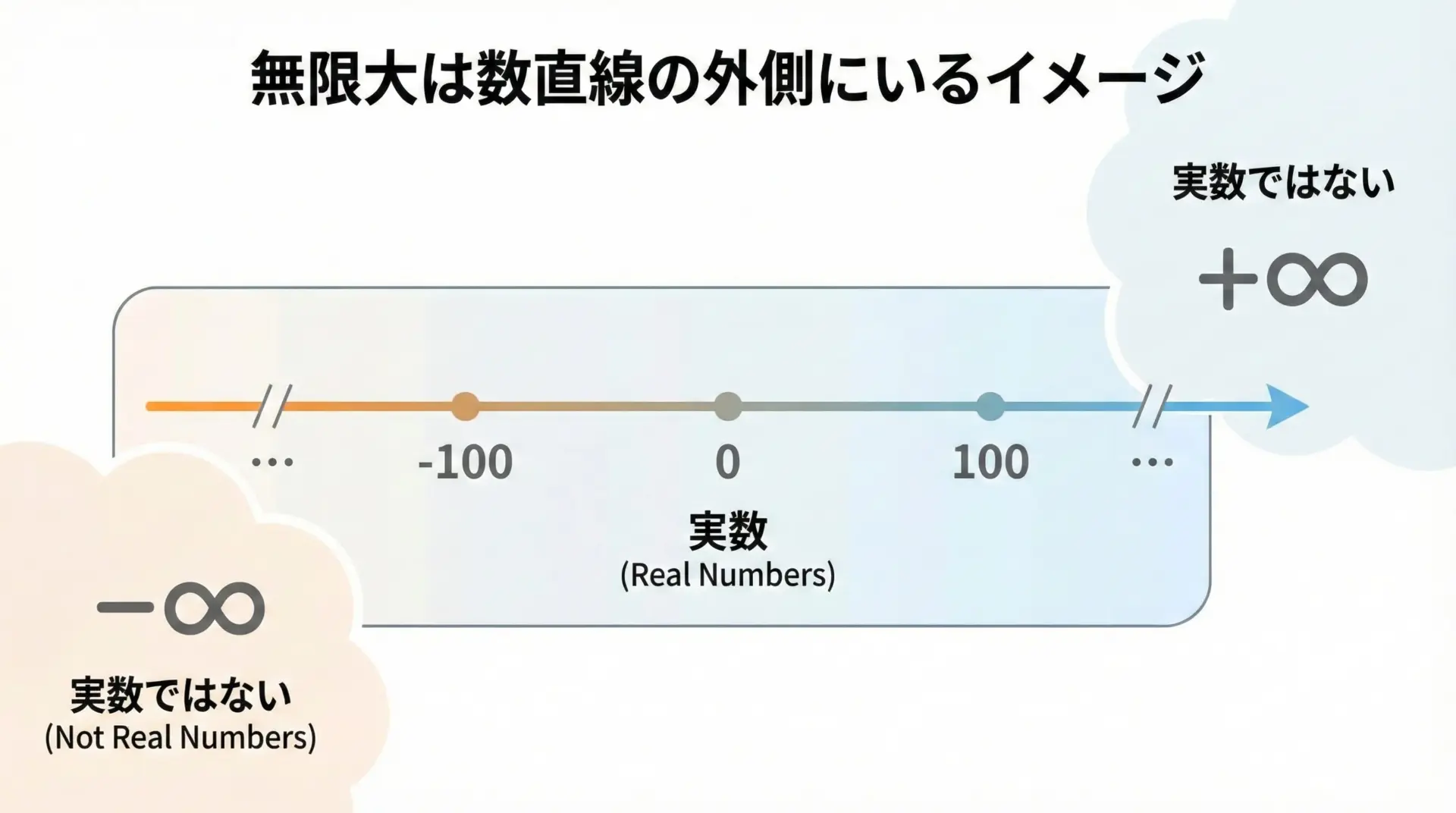
正の無限大(+∞)や負の無限大(−∞)は、ふつうの意味での「数」ではありません。

高校数学では、あくまで「向き」と「限りなく大きい(小さい)」ことを表す記号として使います。

例えば、次のように使います。

x がどれだけ大きくなってもよいときに、x → +∞ と書きます。
x がどれだけ小さく(負方向に大きく)なってもよいときに、x → −∞ と書きます。

ここでのポイントは、「+∞ という具体的な値がある」のではなく、「限りなく大きくなる」という状態を表しているということです。

正の無限大・負の無限大の直感的イメージ

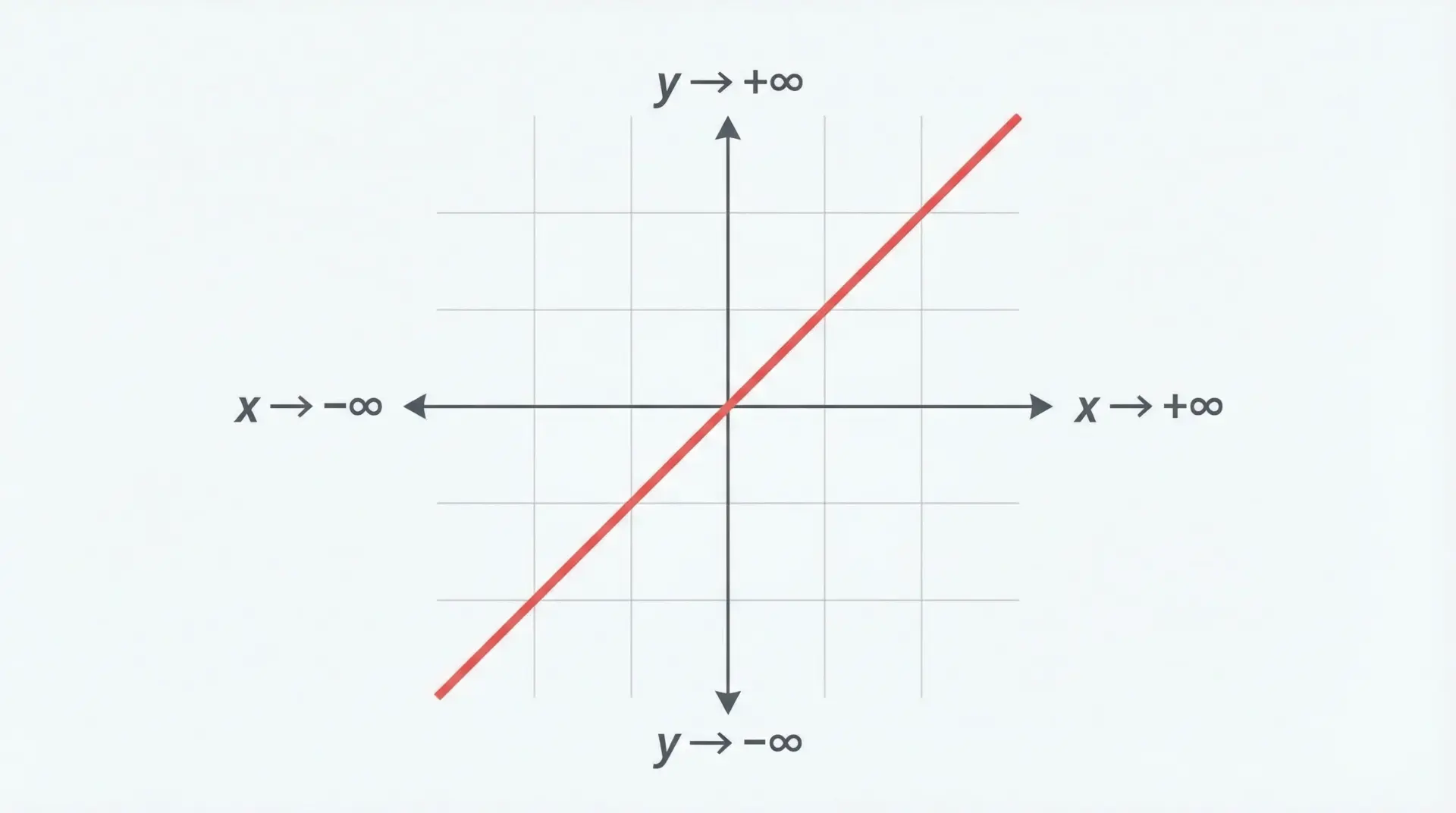
関数y = xを考えると、x が大きくなればなるほど y も大きくなります。

この様子を高校数学では次のように表現します。

x → +∞ のとき y → +∞
x → −∞ のとき y → −∞

ここで、「どこかで +∞ という値を取る」のではなく、「値が限りなく増え続ける様子」を表しているだけです。

このように、正の無限大・負の無限大は、極限の「行き先」を表す目印として登場します。

無限大を使った不等式の読み方

x → +∞ / x → −∞ の意味

x → +∞ は、「x がどんなに大きな数よりもさらに大きくなる」という意味です。

もう少し具体的に言いかえると、次のような日本語になります。

任意の実数 M に対して、x > M が成り立つような x を考えている

同様に、x → −∞ は次のように言いかえられます。

任意の実数 N に対して、x < N が成り立つような x を考えている

どちらも「境目は決めないで、どこまでも突き進む」状態を表している、というイメージが大切です。

「大きさ」を比べるイメージ

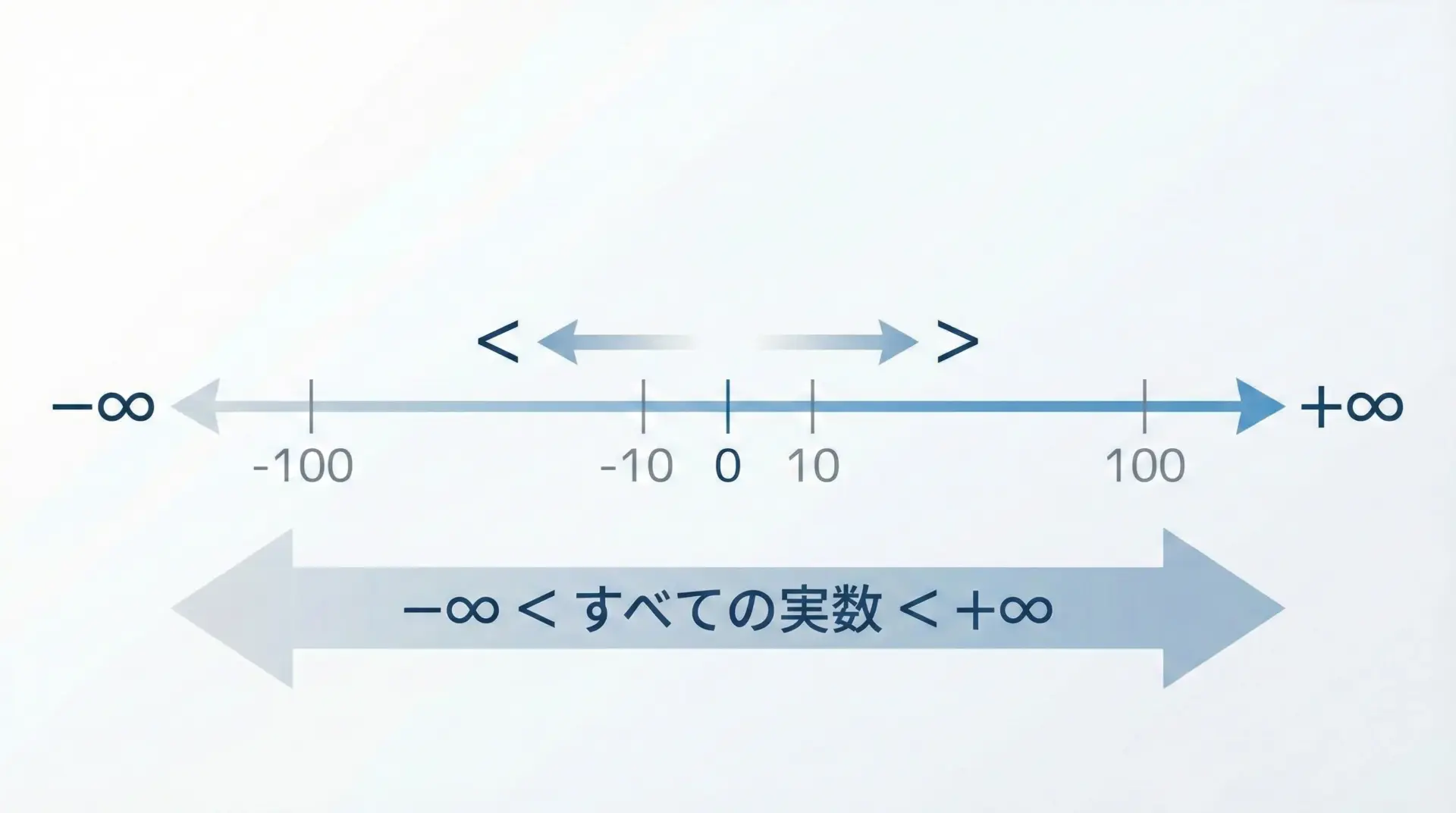
高校数学では、便宜的に次のような大小関係を使います。

−∞ < 実数 < +∞

ここでの「<」や「>」は、厳密な意味の大小ではなく、向きの情報を含んだ記号としての役割が強いものです。

実際の計算では、無限大を「最大の数」「最小の数」として扱わない点に注意が必要です。

無限大と極限の関係

関数の値が無限大に近づくときの表現

関数f(x)について、次のように書くことがあります。

lim(x→+∞) f(x) = +∞
lim(x→+∞) f(x) = 0
lim(x→−∞) f(x) = +∞ など

左側の「x→±∞」は、入力(変数)がどこへ向かうかを示し、右側の「= ±∞」や「= 実数」は、出力(値)がどこへ向かうかを示しています。

簡単な例で確認

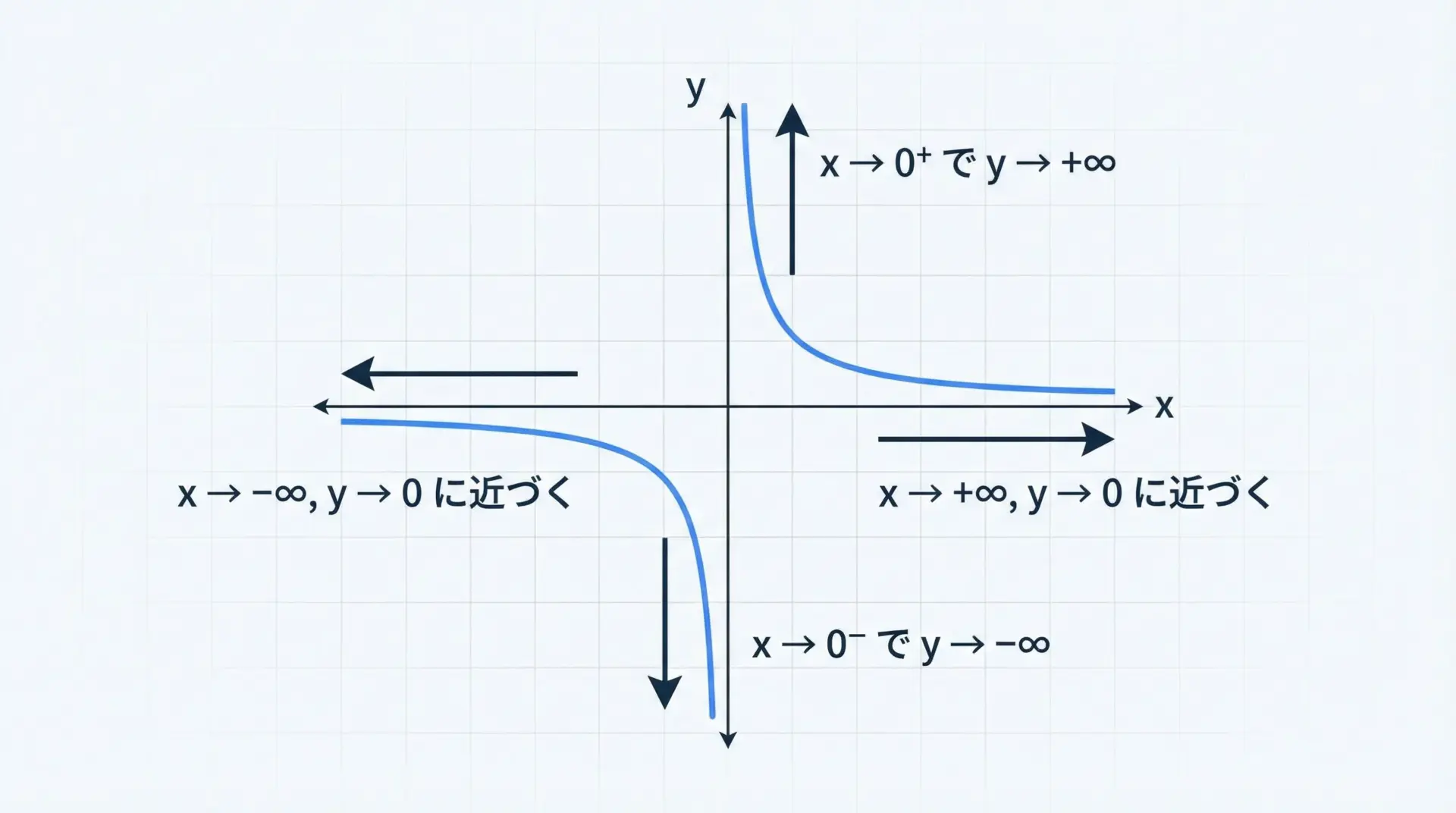
例1: y = 1/x のとき

lim(x→+∞) 1/x = 0
lim(x→−∞) 1/x = 0

これは、x が正でも負でも絶対値が大きくなると 1/x は 0 に近づくという意味です。

例2: y = 1/x² のとき

lim(x→+∞) 1/x² = 0
lim(x→−∞) 1/x² = 0

こちらも同様に 0 に近づきますが、常に正の値から近づくという点が違います。

無限大を含む計算ルール(高校レベル)

「やってよいこと」と「やってはいけないこと」

高校数学では、計算を簡単にするために、無限大を次のように「形式的」に扱うことがあります。

+∞ + 実数 = +∞
−∞ + 実数 = −∞
実数 × (+∞) = ±∞ (符号による)
実数 × (−∞) = ±∞ (符号による)

一方で、次のような式は「不定形」として、そのままでは意味を決めてはいけないものとされます。

∞ − ∞
∞ ÷ ∞
0 × ∞
∞⁰ など

これらは、具体的な関数の形に戻してから、別の方法で極限を計算する必要があります。

よく使う安全なルール

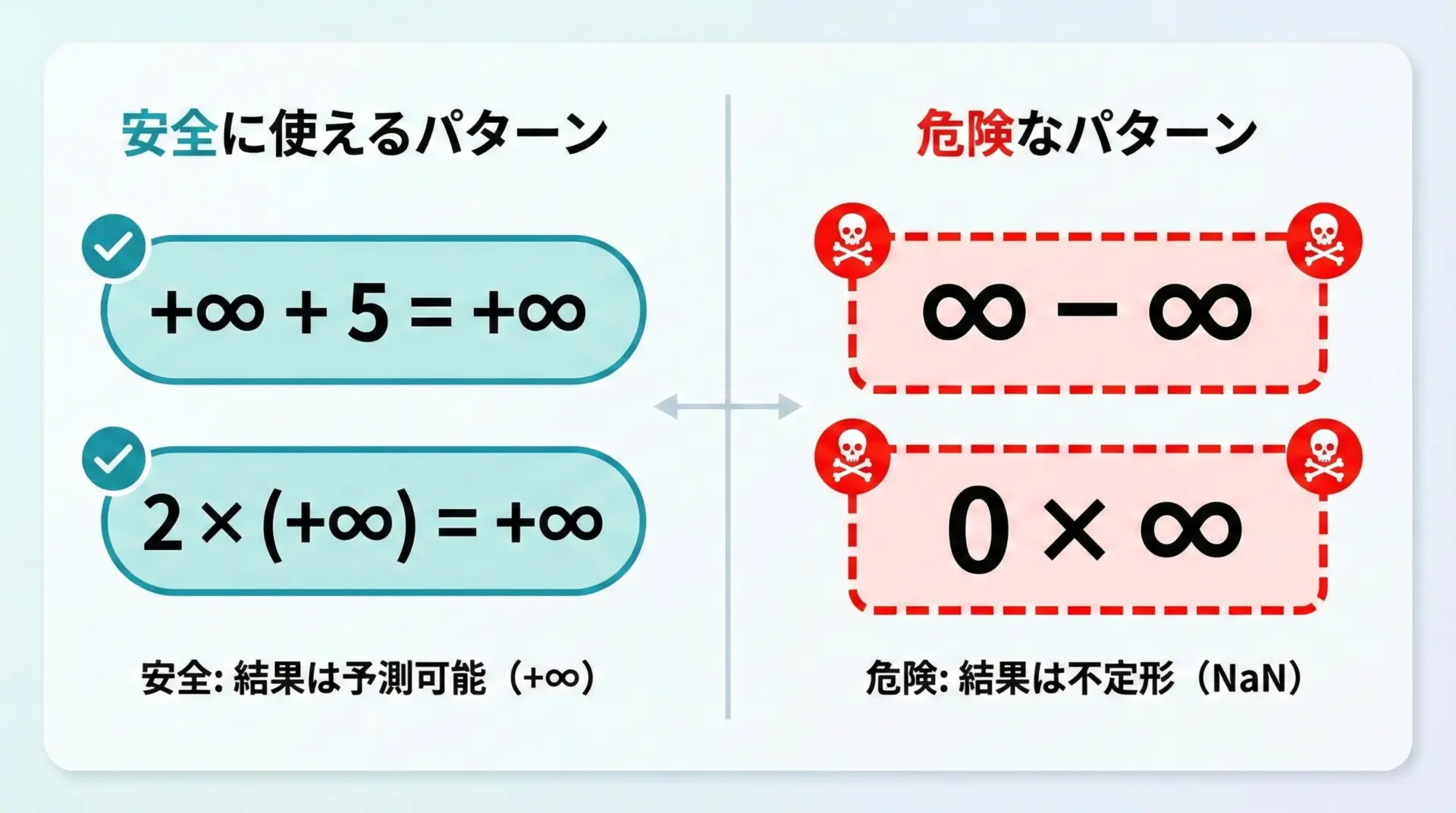
高校レベルで、無限大を形式的に扱ってよい典型例をまとめます。

一方が圧倒的に大きい加法
例:n² + n → +∞ のとき、n²が支配的なので「+∞」と書いてよいと考えます。
符号がはっきりしている積
例:2 × (+∞) = +∞、(−3) × (+∞) = −∞ というイメージで、「正の数×大きくなる」は正側へ、「負の数×大きくなる」は負側へ発散すると理解します。

ただし、これらは「極限の計算を楽に説明するための便宜的なルール」であり、無限大を本当の数として計算しているわけではないことを忘れないでください。

簡単なC言語プログラムで「発散」を観察してみる

ここでは、コンピュータ上で「値がどんどん大きくなっていく様子」を確認して、無限大へのイメージをつかんでみます。

なお、コンピュータには本当の意味での無限大は存在せず、あるところでオーバーフローしてしまうことも合わせて確認します。

ループで値を増やし続ける例

C言語

#include <stdio.h>
#include <math.h>  // 無限大(INFINITY)を使うため

int main(void) {
    double x = 1.0;

    // x を何度も 2 倍していき、どんどん大きくしていく
    for (int i = 0; i < 20; i++) {
        printf("step %2d: x = %e\n", i, x);
        x *= 2.0;  // x を 2 倍
    }

    // C 言語では INFINITY という「正の無限大に相当する特別な値」がある
    double inf = INFINITY;
    double ninf = -INFINITY;

    printf("INFINITY との四則演算の例:\n");
    printf("  INFINITY + 1.0  = %f\n", inf + 1.0);
    printf("  INFINITY * 2.0  = %f\n", inf * 2.0);
    printf("  -INFINITY * 3.0 = %f\n", ninf * 3.0);

    // 危険なパターン(不定形)の例
    printf("危険な(不定形)の例:\n");
    printf("  INFINITY - INFINITY = %f\n", inf - inf);
    printf("  0.0 * INFINITY      = %f\n", 0.0 * inf);

    return 0;
}

上のプログラムを実行すると、おおよそ次のような出力が得られます。

実行結果

step  0: x = 1.000000e+00
step  1: x = 2.000000e+00
step  2: x = 4.000000e+00
step  3: x = 8.000000e+00
...
step 19: x = 5.242880e+05
INFINITY との四則演算の例:
  INFINITY + 1.0  = inf
  INFINITY * 2.0  = inf
  -INFINITY * 3.0 = -inf
危険な(不定形)の例:
  INFINITY - INFINITY = nan
  0.0 * INFINITY      = nan

この出力から、次の点が読み取れます。

値を倍々にしていくと、どんどん大きくなって「発散していく」様子がわかります。
C言語では INFINITY という特別な値を使って、正の無限大っぽい挙動を表現しています。
INFINITY - INFINITY や 0.0 * INFINITY の結果が nan(Not a Number) になるのは、数学でいう不定形をコンピュータが「意味不明」として扱っている、と見ることができます。

高校数学で学ぶ「不定形」の危うさが、コンピュータ上の計算結果としても表れていることがわかります。

まとめ

正の無限大・負の無限大は、実数ではなく「限りなく大きく(小さく)なる様子」を表す記号です。

極限では、x → +∞ や x → −∞ で「入力がどこへ向かうか」を、lim f(x) = +∞ のような形で「値がどこへ向かうか」を表現します。

ただし、∞ − ∞ や 0 × ∞ などは不定形で、そのまま計算してはいけません。

高校レベルでは、無限大を「巨大な数」と誤解せず、「発散の向きを示すマーク」として使い分けることができれば十分です。