なぜNaNはNaNと等しくないのか？奇妙な性質と判定方法

2025年10月24日2026年1月14日

その他

数値計算やプログラミングをしていると、NaN(Not a Number)という少し不思議な存在に出会います。

見た目は数値のようなのに、計算に混ざると結果が全てNaNになったり、自分自身と比較しても等しくならなかったりと、直感に反する動きをします。

本記事では、なぜNaNはNaNと等しくならないのかを中心に、その背後にあるルールや、実務で重要になる「NaN判定の正しい方法」について解説します。

目次 [ close ]

NaNとは何か

NaNの基本的な意味

コンピュータで使われる浮動小数点数(いわゆる小数)は、多くの場合IEEE 754という国際規格に従って表現されています。

この規格の中で「数値として意味のない結果」を表す特別な値として定義されているのがNaNです。

例えば次のような演算結果は、通常の実数として意味を持ちません。

0で割る計算の一部(0.0 / 0.0)
負の数の平方根(sqrt(-1.0))を実数だけで扱おうとしたとき
無限大同士を引く(∞ - ∞)といった曖昧な演算

このような場合に、多くの言語ではNaNが返されます。

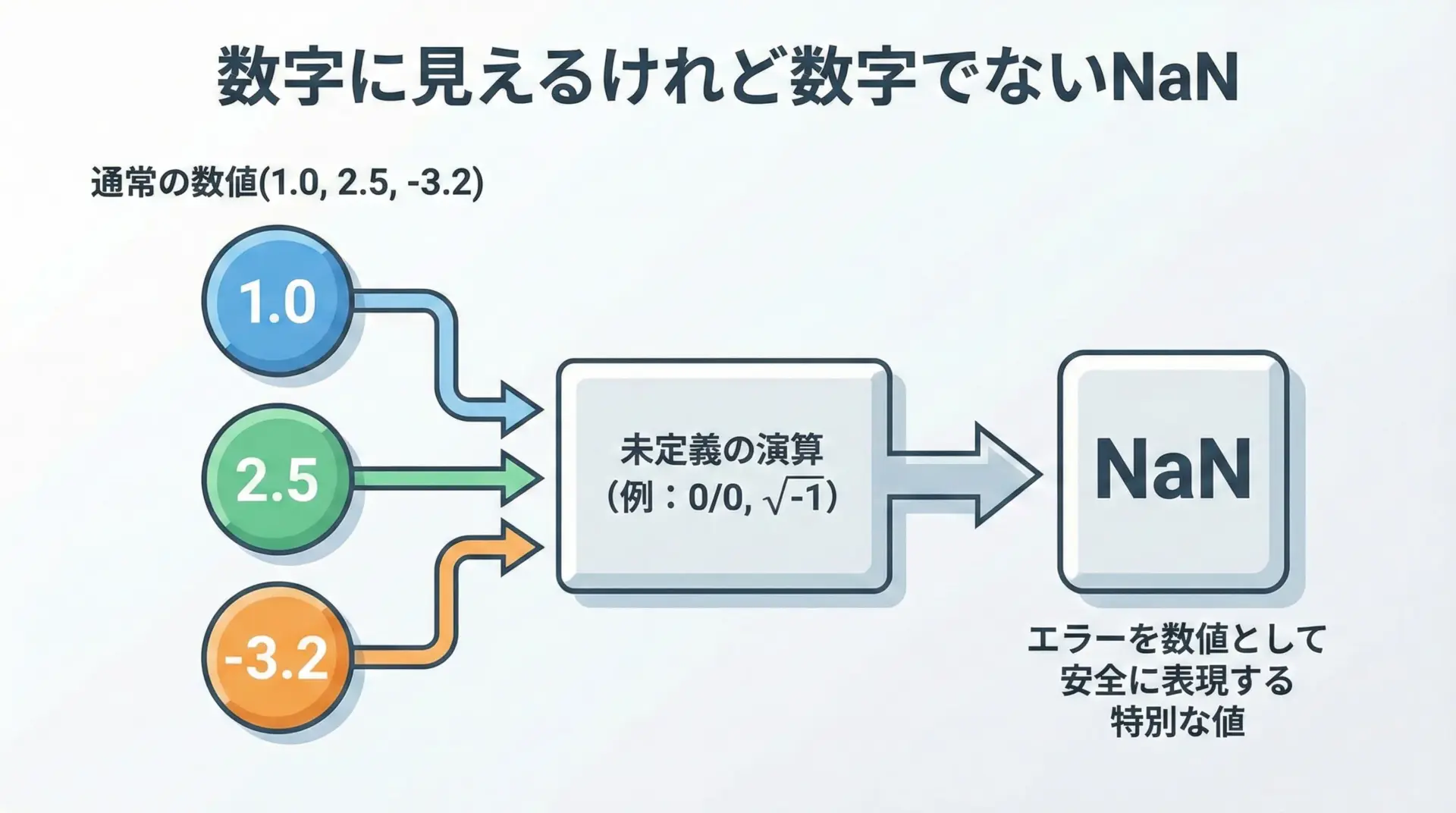
NaNは「エラー」や「未定義」を表すために導入された特別な浮動小数点値だと理解するとイメージしやすくなります。

なぜNaNはNaNと等しくないのか

比較の常識とNaNの非常識

整数などの普通の値については、同じ値同士なら等しいと判断されます。

1と1は等しい
14と3.14は等しい

ところが、NaNの場合はNaN == NaN が偽(false)になります。

これはバグではなく、IEEE 754規格で明示的にそう決められている仕様です。

背景にある「部分順序」という考え方

通常の数値は「大小関係」の線上にきれいに並べることができますが、NaNはこの線のどこにも置くことができません。

NaNは「この値は数直線上のどこにも位置づけられない」という意味を持っているため、次のような思想で設計されています。

NaNは、どの数値とも「等しい」とは言えない
NaNは、どの数値より「大きい」とも「小さい」とも言えない
NaN同士であっても「同じ種類の未定義」とは限らないから等しいとは言えない

つまり、「値としての中身が比較不能なので、どんな順序関係にも参加しない」という設計になっています。

これを実現するため、NaNを含む全ての比較演算(==, !=, <, >, <=, >=)は、特別な扱いを受けます。

IEEE 754におけるNaN比較ルール

比較の結果がどうなるか

IEEE 754では、NaNを含む比較は次のようなルールになっています。

NaN == 何か → 常にfalse
NaN != 何か → 常にtrue
NaN < 何か → false
NaN > 何か → false
NaN <= 何か → false
NaN >= 何か → false

そのため「どの比較演算子を使っても、NaNを含むとまともな順序づけはできない」という結果になります。

次の表は、具体例としてC言語風の比較を示したものです。

式	結果
NaN == NaN	false
NaN != NaN	true
NaN == 1.0	false
NaN != 1.0	true
NaN < 1.0	false
NaN > 1.0	false
NaN <= 1.0	false
NaN >= 1.0	false

このように、「不等号を使ってもNaNをはじき出すことはできない」ことに注意する必要があります。

直感的なイメージ

NaNを「答えが壊れていて、まだ中身が確認できない箱」のように考えると理解しやすくなります。

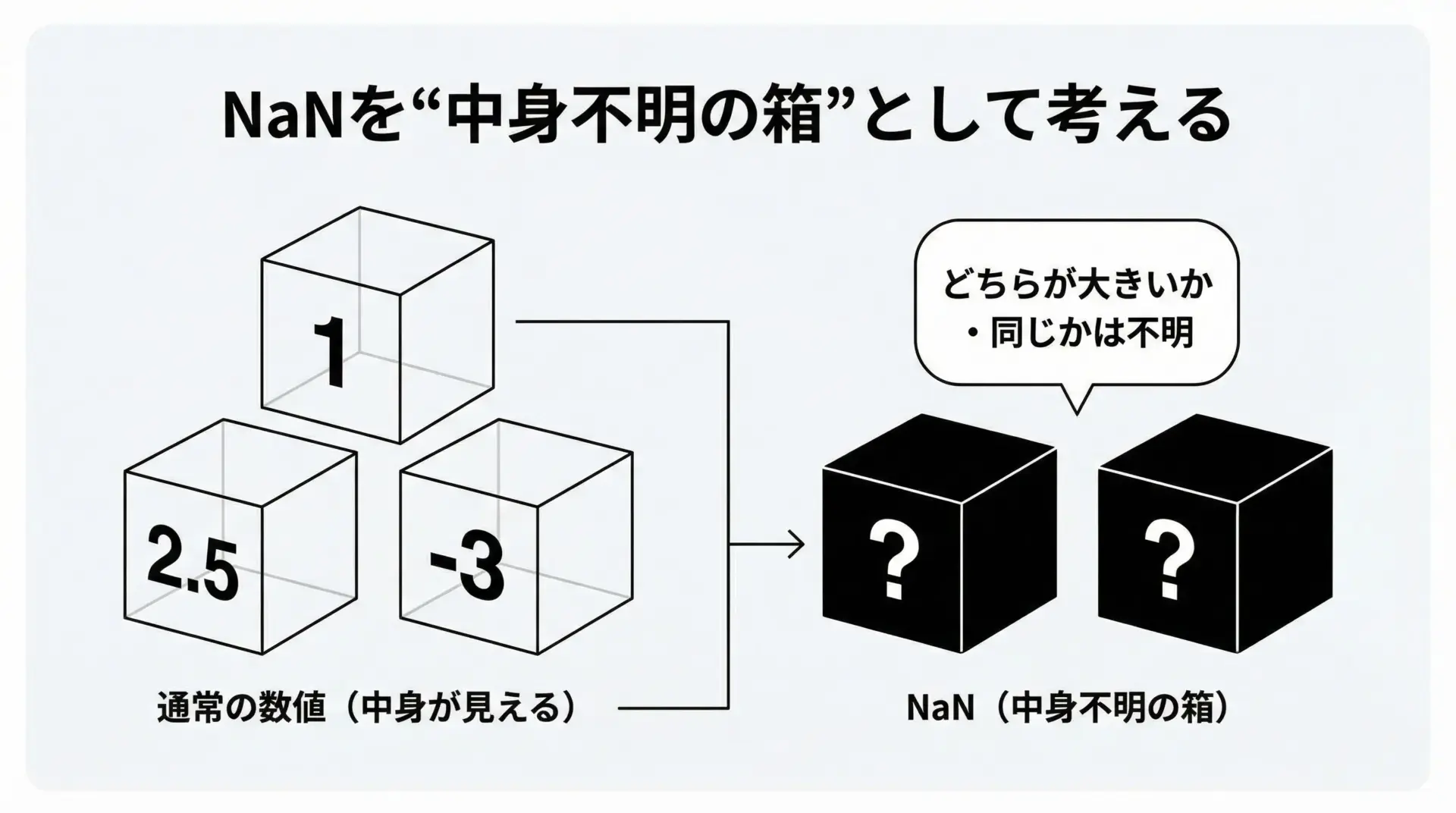
中身が不明な箱同士を見比べても、「同じ中身」かどうかはわからないので、等しいとも等しくないとも判断できません。

IEEE 754では、その結果を「等しくない比較はすべてfalse、唯一!=だけtrueにする」という規則として定めています。

プログラミング言語でのNaNの挙動

ここではC言語を例に、NaNがどのように振る舞うかを実際のコードで確認します。

C言語でのNaN比較サンプル

C言語

#include <stdio.h>
#include <math.h>   // isnan, NAN

int main(void) {
    double x = 0.0 / 0.0;  // 0.0を0.0で割ると多くの環境でNaNになる
    double y = NAN;        // 明示的にNaNを作るマクロ(NAN)もある

    printf("x = %f, y = %f\n", x, y);

    // 1. NaN同士の比較
    printf("x == y : %d\n", x == y);   // 期待に反して0(false)
    printf("x != y : %d\n", x != y);   // 1(true)

    // 2. NaNと通常の数値との比較
    double a = 1.0;
    printf("x == a : %d\n", x == a);   // 0(false)
    printf("x <  a : %d\n", x <  a);   // 0(false)
    printf("x >  a : %d\n", x >  a);   // 0(false)

    // 3. isnanによる判定
    printf("isnan(x): %d\n", isnan(x)); // 1(true)
    printf("isnan(a): %d\n", isnan(a)); // 0(false)

    return 0;
}

実行結果

x = nan, y = nan
x == y : 0
x != y : 1
x == a : 0
x <  a : 0
x >  a : 0
isnan(x): 1
isnan(a): 0

このコード例から、比較演算子ではNaNを検出できず、専用の判定関数を使う必要があることがよくわかります。

NaNを正しく判定する方法

直接比較が使えない理由

前述の通り、NaN == NaN はfalseです。

そのため、次のようなコードは意図通りに動作しません。

C言語

// これは意図通りに動作しないNG例
if (x == NAN) {
    printf("xはNaNです\n");
}

この条件式は「どんな場合でもfalseになる」ため、xがNaNであってもメッセージは出力されません。

専用の判定関数を用いる

多くの言語やライブラリでは、NaNを判定するための専用関数が用意されています。

C言語の場合はisnan、C++ではstd::isnan、Pythonではmath.isnanなどが該当します。

C言語での正しい判定例は次のようになります。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double x = 0.0 / 0.0;  // NaN

    // NaNの正しい判定方法
    if (isnan(x)) {
        printf("xはNaNです\n");
    } else {
        printf("xはNaNではありません\n");
    }

    return 0;
}

実行結果

xはNaNです

このように「NaNかどうか」を調べるときは常に専用関数を使うと覚えておくと、安全で読みやすいコードを書くことができます。

NaNの「うつりやすさ」と実務上の注意点

一度NaNになると計算結果が次々NaNになる

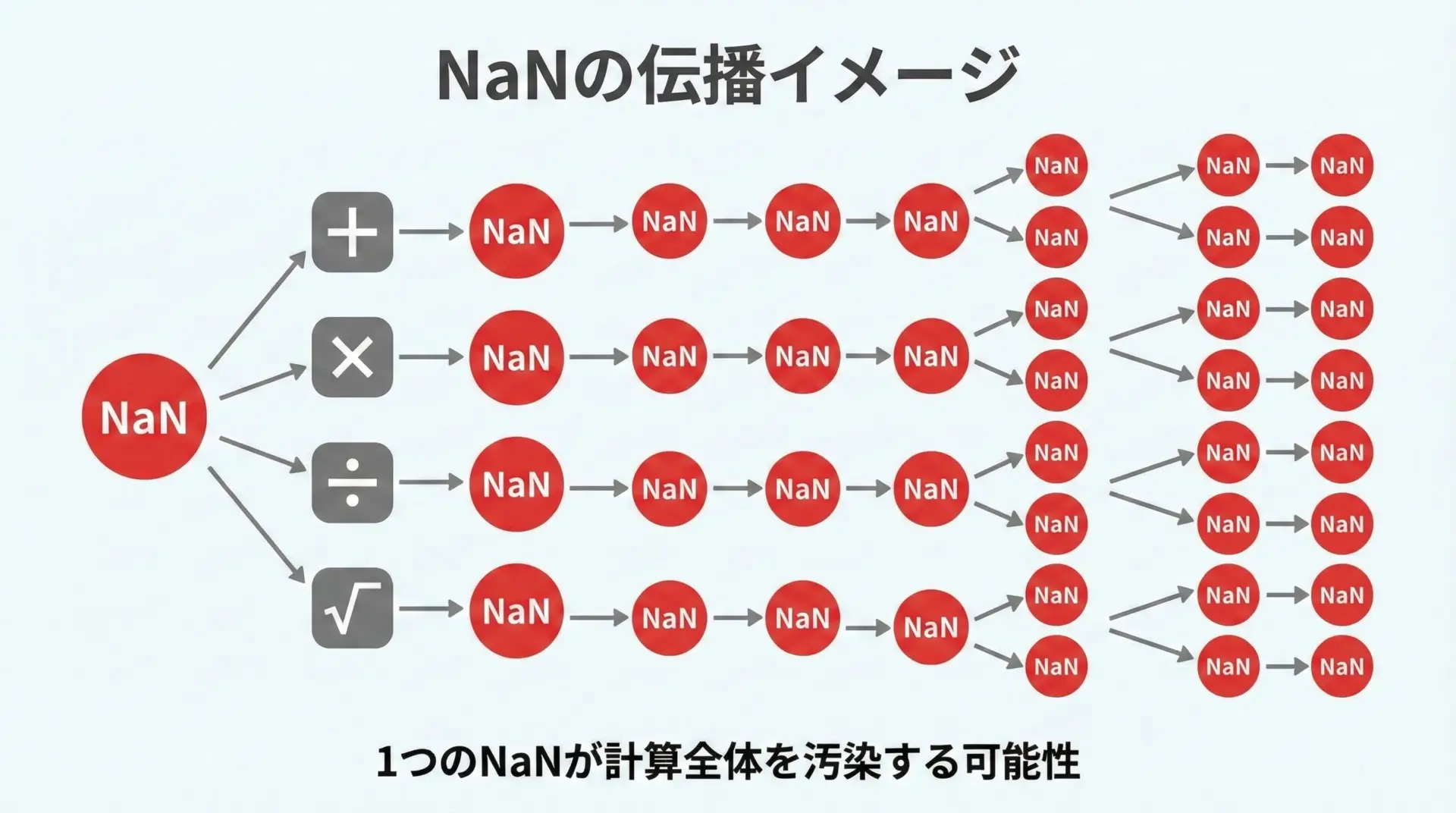
NaNは、演算を通じてどんどん伝播する性質を持ちます。

NaN + 1.0 → NaN
NaN * 2.0 → NaN
sqrt(NaN) → NaN

そのため、どこか1カ所でNaNが発生すると、後続の多くの計算結果がNaNに染まってしまい、原因特定が難しくなることがあります。

バグ発見のための実用的なポイント

実務や学習でNaNと付き合う際には、次の点を意識するとトラブルを避けやすくなります。

不自然な計算結果(突然グラフが崩れるなど)が出たときは、途中結果にNaNが紛れ込んでいないかを疑う
重要な中間変数について、isnanでチェックするログを一時的に仕込む
ユーザー入力や外部データから読み込んだ値は、必ず検証してから計算に使う

このように、NaNは「エラーを表す便利な仕組み」である一方、放置すると計算全体の信頼性を損なう危険な値でもあります。

まとめ

NaNはIEEE 754で定義された「数値として意味を持たない結果」を表す特別な値です。

意味が不明な値であるため、数直線上のどこにも位置づけられず、NaN == NaN がfalseになるという、一見すると奇妙な仕様が生まれました。

比較演算子ではNaNを正しく扱えないため、実務では専用のNaN判定関数(isnanなど)を用いることが重要です。

また、一度NaNが発生すると計算全体に広がりやすいため、途中結果のチェックや入力値の検証によって早期に検出することが、堅牢な数値計算やプログラム設計の鍵になります。