算術右シフトと論理右シフトは、右にビットをずらすという意味では同じですが、負の数を扱うときに大きな違いが生まれます。
本記事では、初心者の方にも分かるように、図解と具体例、C言語のサンプルコードを用いながら、両者の違いと使い分けを丁寧に解説します。
ビット演算の基礎理解にもつながりますので、ぜひ最後まで読み進めてみてください。
算術右シフトと論理右シフトとは
ビットシフトの基本イメージ
ビットシフトとは、整数を構成しているビット列を左右にずらす演算のことです。
右シフトは名前の通り、ビット列を右側へずらします。
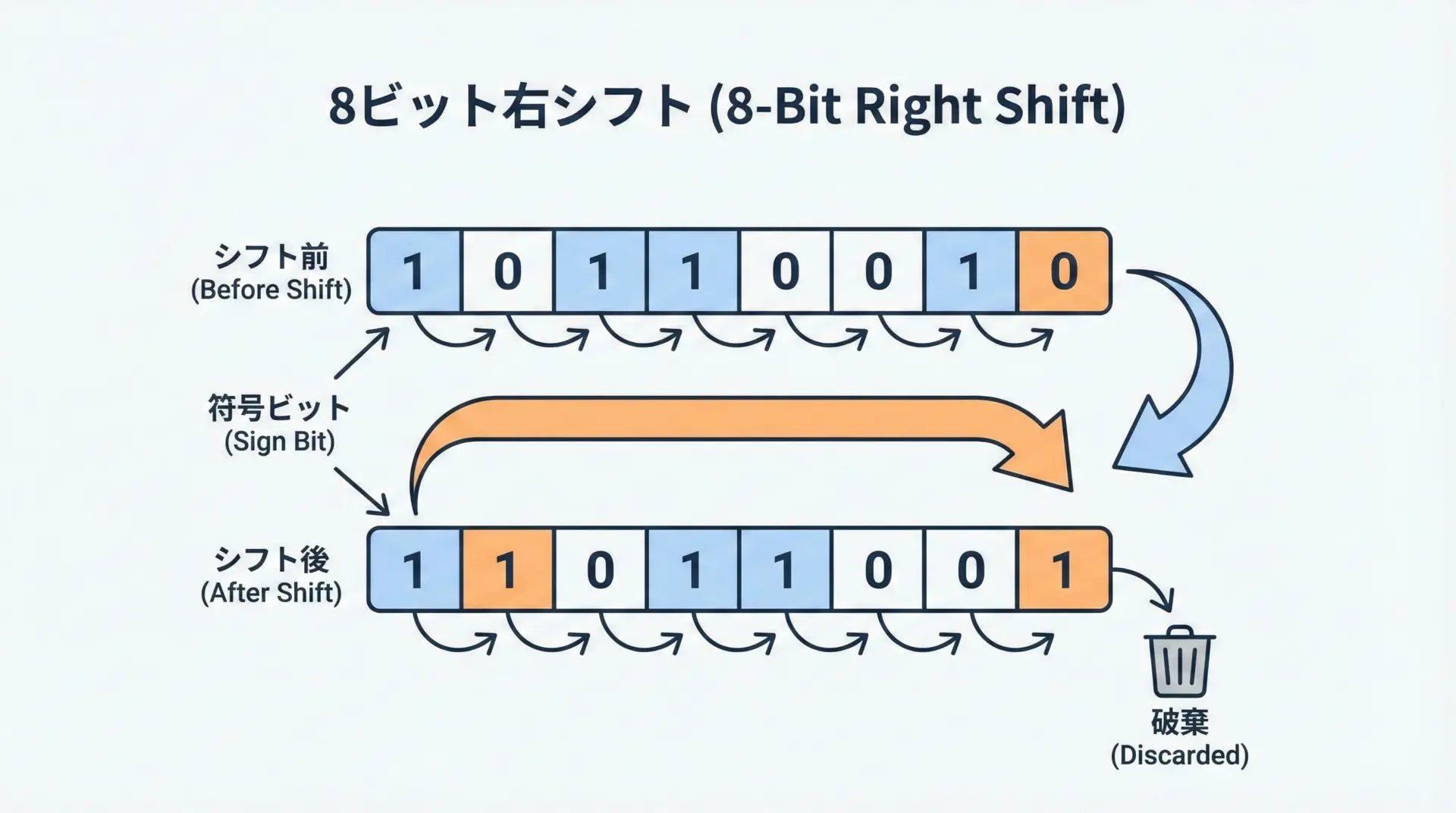
右へ1ビットずらすごとに、2で割ったような効果が表れますが、そのときに左端の空いたビットを何で埋めるかで、算術右シフトと論理右シフトの違いが生まれます。
算術右シフトとは
算術右シフトは、主に「符号付き整数」に対して使われる右シフトです。
2の補数表現の負数を含む整数で、値の正負を保ちながら右シフトすることを目的としています。
算術右シフトでは、右にずれたことで空いた最上位ビット(符号ビット)を、もとの符号ビットと同じ値で埋めます。
つまり、元が正の数なら0で埋まり、負の数なら1で埋まります。
これにより、値をおおむね「2で割る」方向に変化させつつ、正負は維持されます。
論理右シフトとは
論理右シフトは、主に「符号なし整数」に対して使われます。
ビット列を単なる0と1の並びとして扱い、数値の符号を考えずにシフトします。
論理右シフトでは、右にずれたことで空いた最上位ビットを必ず0で埋めます。
そのため、負数表現の2の補数をそのまま右シフトすると、符号が変わってしまうことがあります。
論理シフトは、ビットフラグ処理やマスク処理など、符号を意識しないビット操作でよく使われます。
2進数と符号ビットの復習
2の補数表現のざっくり復習
コンピュータでは、多くの場合、整数を2の補数表現で保存します。
簡単にまとめると次のようになります。
| 種類 | 8ビット例 | 意味 |
|---|---|---|
| 正の数 | 00000101 | 5 |
| 負の数 -5 | 11111011 | -5(2の補数) |
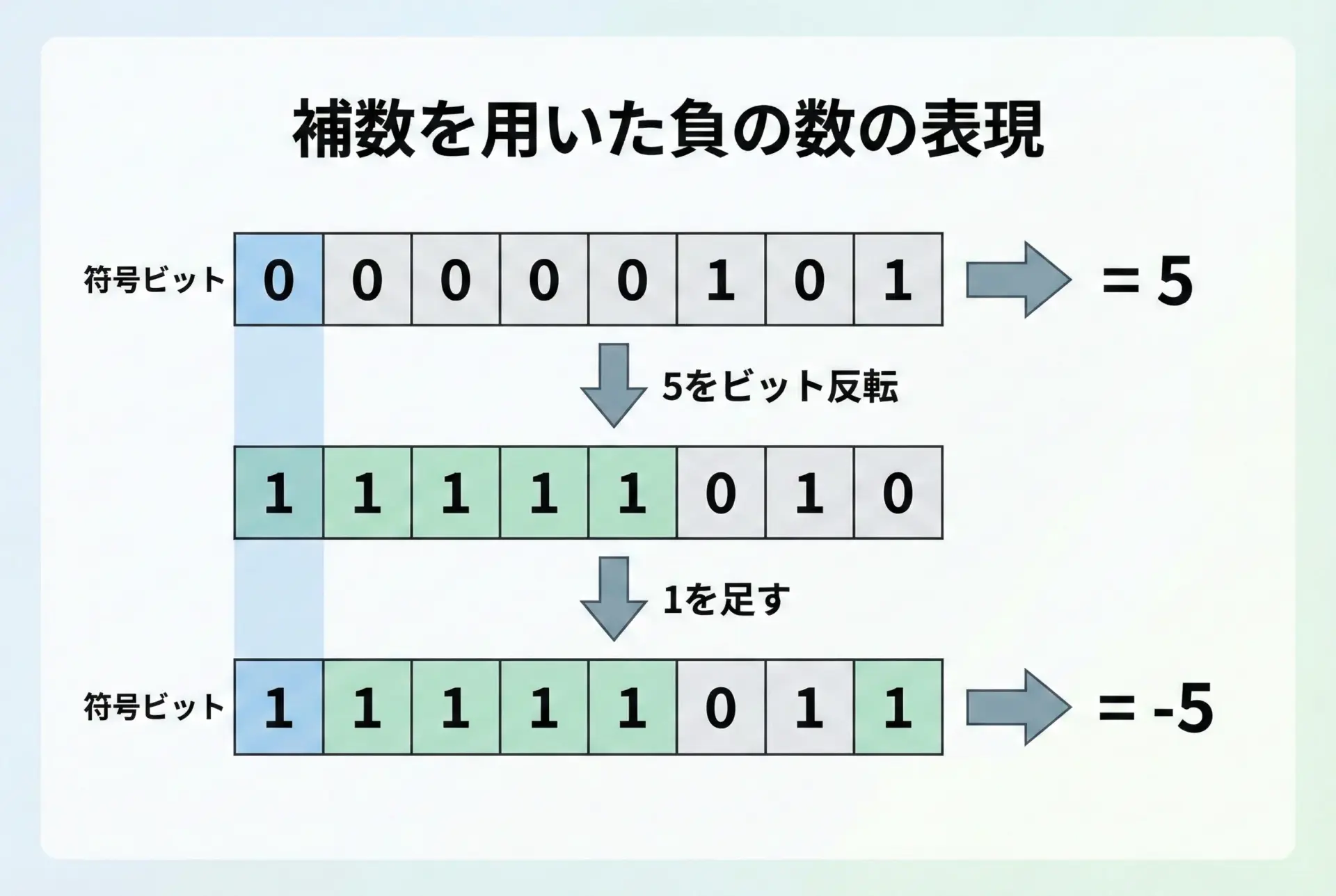
負の数 -5 を2の補数で作るときは、次の手順になります。
- 5を2進数で表す(00000101)
- ビットを反転する(11111010)
- 1を加える(11111011)
このように、負数では左端のビット(最上位ビット)が1になることが多く、これを符号ビットとして扱います。
算術右シフトでは、この符号ビットを維持することが重要になります。
算術右シフトの具体例
正の数の算術右シフト
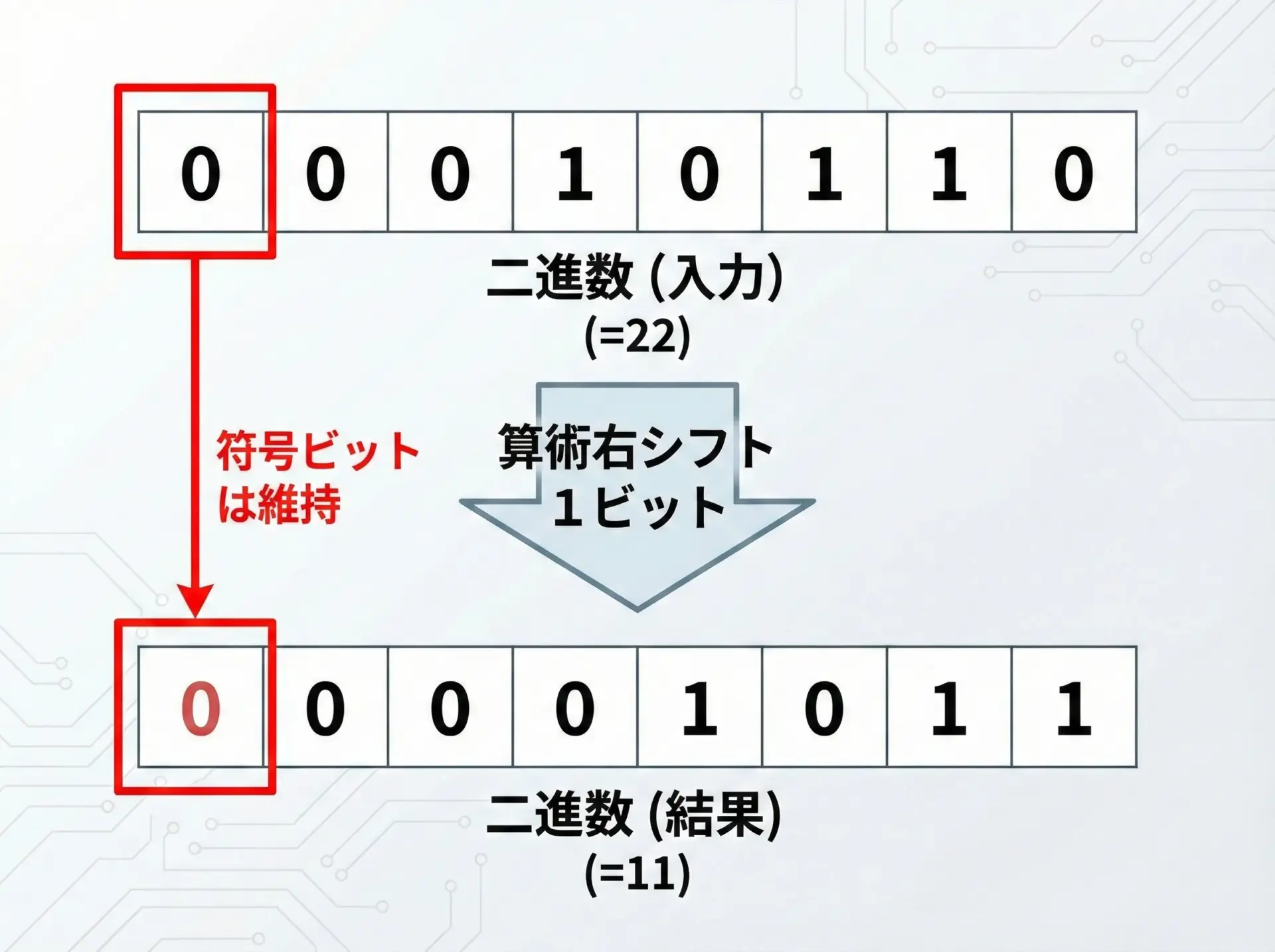
22を8ビットで表すと次のようになります。
| 値 | 2進数(8ビット) |
|---|---|
| 22 | 00010110 |
これを算術右シフト1ビットすると、次のようになります。
- シフト前: 00010110
- シフト後: 00001011
左端のビットは0のまま維持されるので、最終的な値は2進数で00001011、10進数で11となります。
おおよそ2で割った値になっていることが分かります。
負の数の算術右シフト
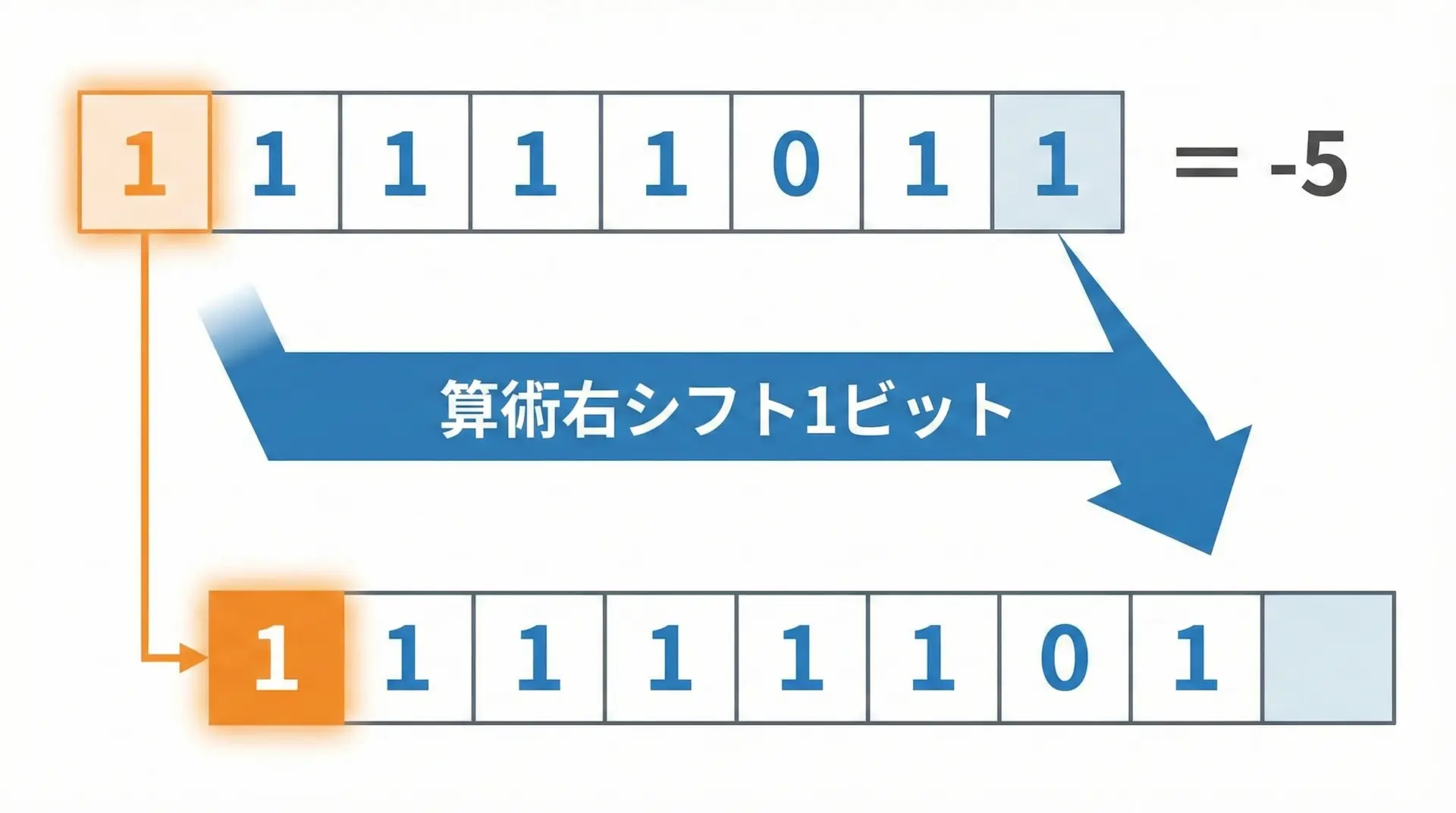
先ほどの -5 の例を使います。
| 値 | 2進数(8ビット) |
|---|---|
| -5 | 11111011 |
これを算術右シフト1ビットすると、次のようになります。
- シフト前: 11111011
- シフト後: 11111101
左端の最上位ビットが1のまま維持されていることがポイントです。
結果の11111101は、2の補数として解釈すると -3 になります。
-5を2で割ると -2.5 ですが、整数なので0方向ではなく負の方向へ丸められ、-3 になる実装が多いです(言語仕様によって細かい扱いは異なることがあります)。
ここから算術右シフトは「符号付きの除算に近い動きをする」ことがイメージできると思います。
論理右シフトの具体例
正の数の論理右シフト
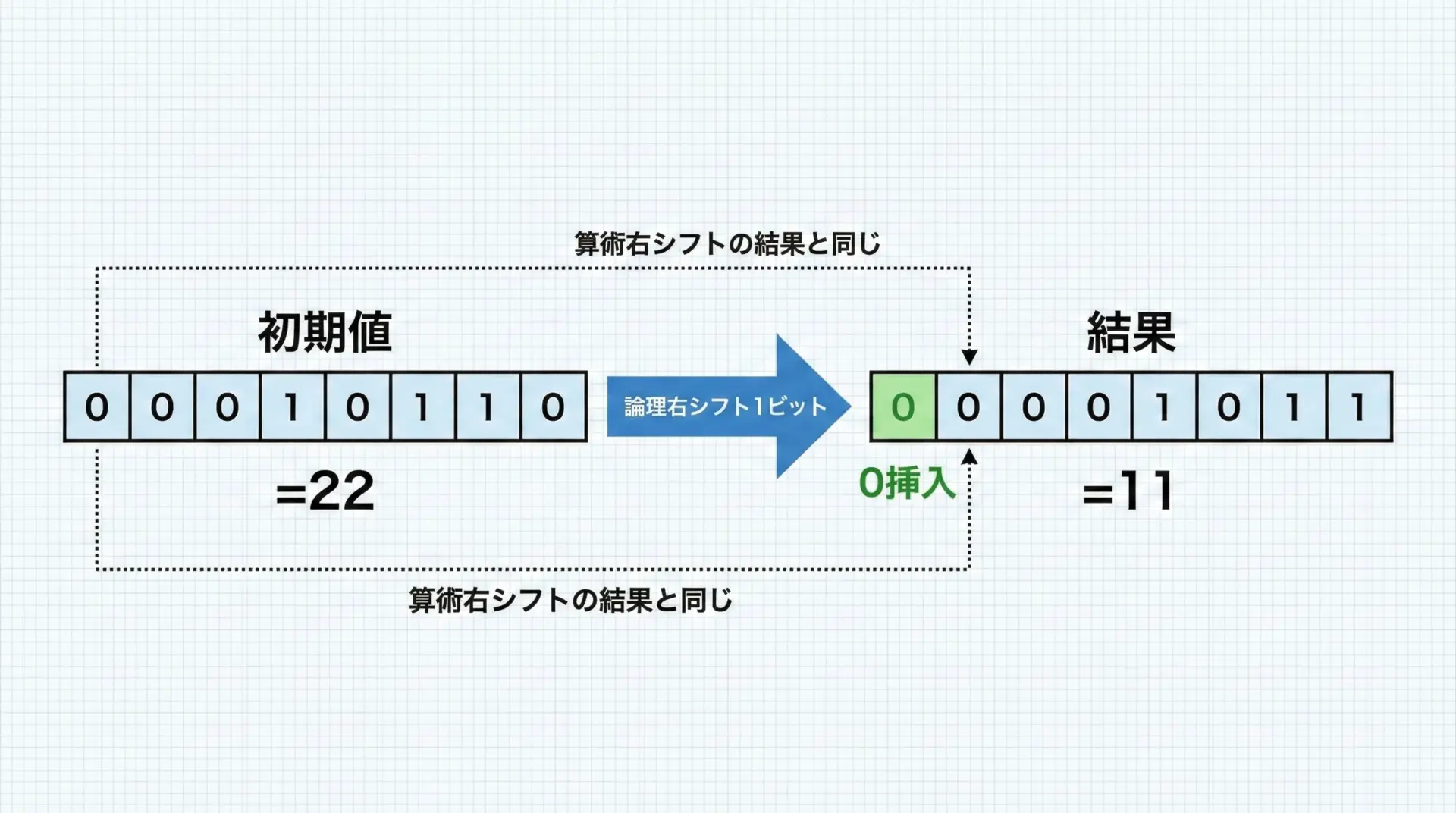
正の数に対しては、論理右シフトも算術右シフトも結果が同じになることが多いです。
22(00010110)に対して論理右シフト1ビットを行うと、次のようになります。
- シフト前: 00010110
- シフト後: 00001011(空いた左端ビットを0で埋める)
この結果は、算術右シフトと同じになります。
負の数の論理右シフト
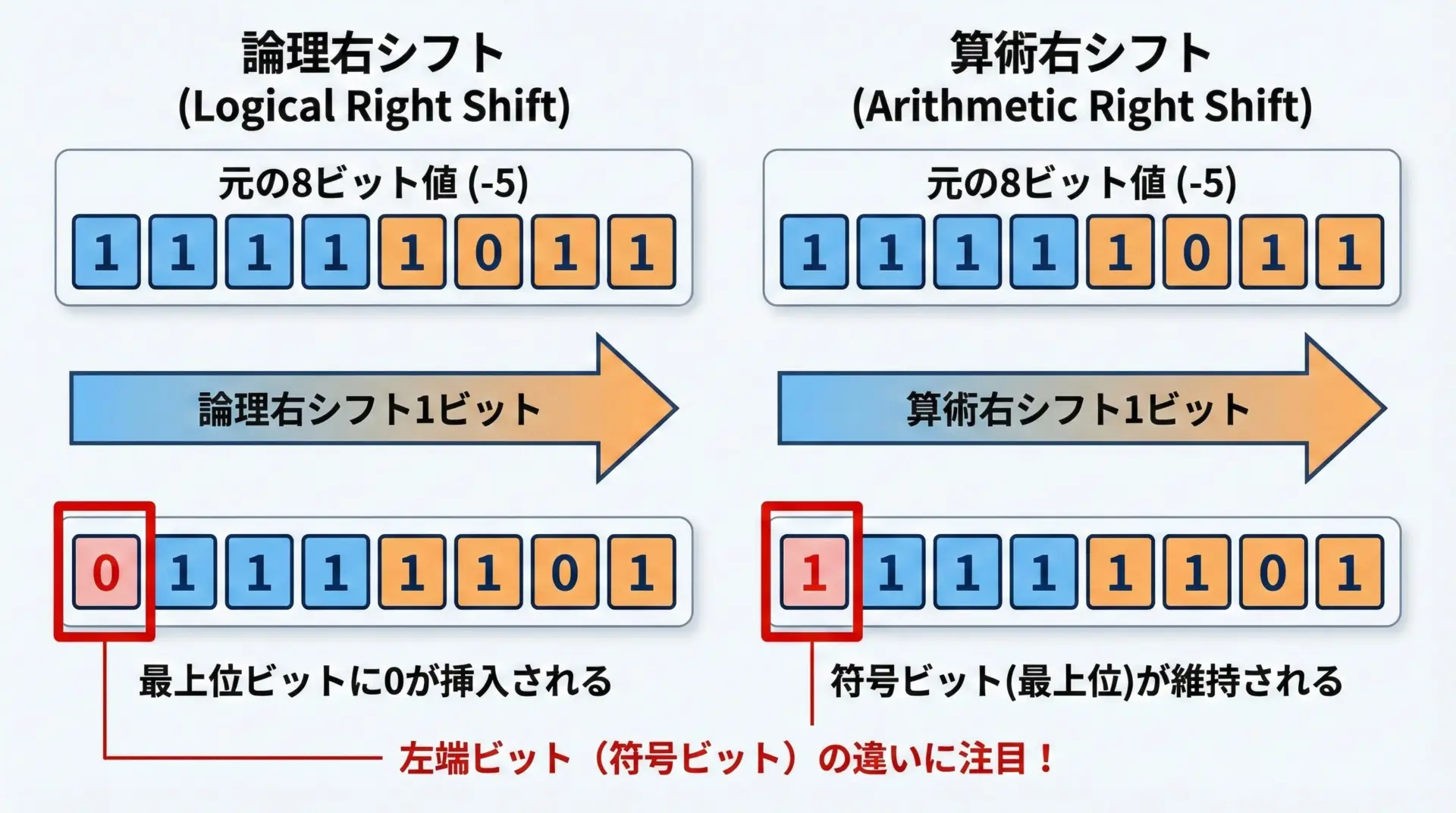
同じ -5(11111011) に対して論理右シフト1ビットを行うと、最上位ビットは必ず0で埋められます。
- シフト前: 11111011
- シフト後: 01111101
結果の01111101は、符号付きとして解釈すると正の数になります。
これは10進数で 125 です。
元が -5 だったにもかかわらず、論理右シフトでは符号が変わってしまったことが分かります。
このように、論理右シフトは「符号を保つ」という考えを一切持たず、単なるビット列のずらしとして動作します。
算術右シフトと論理右シフトの違いまとめ
振る舞いの違いを一覧で確認
| 項目 | 算術右シフト | 論理右シフト |
|---|---|---|
| 主な対象 | 符号付き整数 | 符号なし整数 |
| 左端に埋めるビット | 元の符号ビット(0または1) | 常に0 |
| 正の数の結果 | おおむね2で割る動き | おおむね2で割る動き(同じになることが多い) |
| 負の数の結果 | おおむね負のまま1ビット右シフト | 時に正の数に変わる |
| 用途 | 符号付きの演算、簡易的な除算など | ビットマスク、フラグ処理など |
最大の違いは「左端ビットを何で埋めるか」と「負の数をどう扱うか」です。
算術右シフトは符号を保ち、論理右シフトは符号を無視します。
C言語で動作を確認するサンプルコード
ここではC言語を使って、算術右シフトと論理右シフトの違いを実際に確認してみます。
C言語ではint型の右シフトは多くの処理系で算術右シフトになり、unsigned int型の右シフトは論理右シフトになります(標準規格上は注意点がありますが、ここでは代表的な挙動として扱います)。
#include <stdio.h>
#include <stdint.h>
int main(void) {
// 符号付きと符号なしで同じビットパターンを用意
int8_t s_neg = -5; // 符号付き8ビット(-5)
int8_t s_pos = 22; // 符号付き8ビット(22)
uint8_t u_val = 0b11111011; // 符号なし8ビット(ビット列は11111011)
printf("=== 元の値 ===\n");
printf("s_neg (int8_t) = %d\n", s_neg);
printf("s_pos (int8_t) = %d\n", s_pos);
printf("u_val (uint8_t) = %u\n", u_val);
// 右シフト1ビット
int8_t s_neg_shift = s_neg >> 1; // 多くの処理系で算術右シフト
int8_t s_pos_shift = s_pos >> 1; // 正の数の算術右シフト
uint8_t u_val_shift = u_val >> 1; // 論理右シフトとして動くことが多い
printf("\n=== 右シフト結果(1ビット) ===\n");
printf("s_neg >> 1 (int8_t) = %d\n", s_neg_shift);
printf("s_pos >> 1 (int8_t) = %d\n", s_pos_shift);
printf("u_val >> 1 (uint8_t) = %u\n", u_val_shift);
// ビット列を表示するための補助ループ
printf("\n=== ビット列の確認(8ビット) ===\n");
// 符号付き -5 のビット列と、その右シフト結果
printf("s_neg : ");
for (int i = 7; i >= 0; --i) {
printf("%d", (s_neg >> i) & 1);
}
printf("\n");
printf("s_neg >> 1 : ");
for (int i = 7; i >= 0; --i) {
printf("%d", (s_neg_shift >> i) & 1);
}
printf("\n\n");
// 符号なし u_val のビット列と、その右シフト結果
printf("u_val : ");
for (int i = 7; i >= 0; --i) {
printf("%d", (u_val >> i) & 1);
}
printf("\n");
printf("u_val >> 1 : ");
for (int i = 7; i >= 0; --i) {
printf("%d", (u_val_shift >> i) & 1);
}
printf("\n");
return 0;
}想定される実行結果例
実行環境によって細かい出力は異なる場合がありますが、多くの環境では次のような結果になります。
=== 元の値 ===
s_neg (int8_t) = -5
s_pos (int8_t) = 22
u_val (uint8_t) = 251
=== 右シフト結果(1ビット) ===
s_neg >> 1 (int8_t) = -3
s_pos >> 1 (int8_t) = 11
u_val >> 1 (uint8_t) = 125
=== ビット列の確認(8ビット) ===
s_neg : 11111011
s_neg >> 1 : 11111101
u_val : 11111011
u_val >> 1 : 01111101この結果から次のことが分かります。
- 符号付き -5(int8_t) の右シフトでは、左端ビットが1のまま保たれ、算術右シフトのように動作して -3 になっています。
- 符号なし 251(uint8_t) の右シフトでは、左端ビットが0で埋められ、論理右シフトとして動作し、125 になっています。
- 同じビット列11111011でも、型(符号付きか符号なしか)によって意味も結果も変わることが重要です。
どちらを使うべきかの目安
符号付き整数なら算術右シフトが基本
「負の数も扱う整数の計算」で、右シフトを使って2で割るような操作をしたい場合は、算術右シフトが適しています。
C言語では、intやlongなどの符号付き型で>>を使うと、多くの処理系で算術右シフトになります。
ただし、言語仕様や処理系によっては挙動が未定義または実装依存になることもあるため、厳密な数値計算では/ 2のような通常の除算を使うほうが安全です。
ビットフラグ処理なら論理右シフトが基本
ビットフラグ、マスク処理、プロトコル解析など「ビット列として扱うデータ」では、符号を持たないunsigned型を使い、論理右シフトで操作するのが一般的です。
- 上位ビットにフラグを詰め込んでいる場合
- ネットワークパケットのヘッダを解析する場合
- 画像処理や暗号処理などでビット列を直接操作する場合
これらでは、最上位ビットを必ず0で埋める論理右シフトのほうが意図した動きに近くなります。
まとめ
算術右シフトと論理右シフトは、どちらもビット列を右へずらす演算ですが、「左端ビットを何で埋めるか」と「負の数の扱い」が決定的に違います。
算術右シフトは符号ビットを保つため、符号付き整数の簡易的な除算に向いています。
一方、論理右シフトは最上位ビットを常に0で埋めるため、符号なし整数のビット操作に向いています。
特に、同じ>>演算子でも、型が符号付きか符号なしかで意味が変わる点は、バグの原因になりやすいポイントです。
整数の型とシフトの意味を意識しながら、状況に応じて正しく使い分けるようにしてください。