コンピュータで数値を扱うときには、表現できる範囲に限界があります。
その限界を超えるとオーバーフローやアンダーフローと呼ばれる現象が起こり、思いもよらない結果になることがあります。
本記事では、整数と浮動小数点の両方について、この2つの現象を図解とサンプルコードを交えながらやさしく解説します。
数値表現と範囲のイメージをつかむ
コンピュータの数は「有限のメモリ箱」で表される
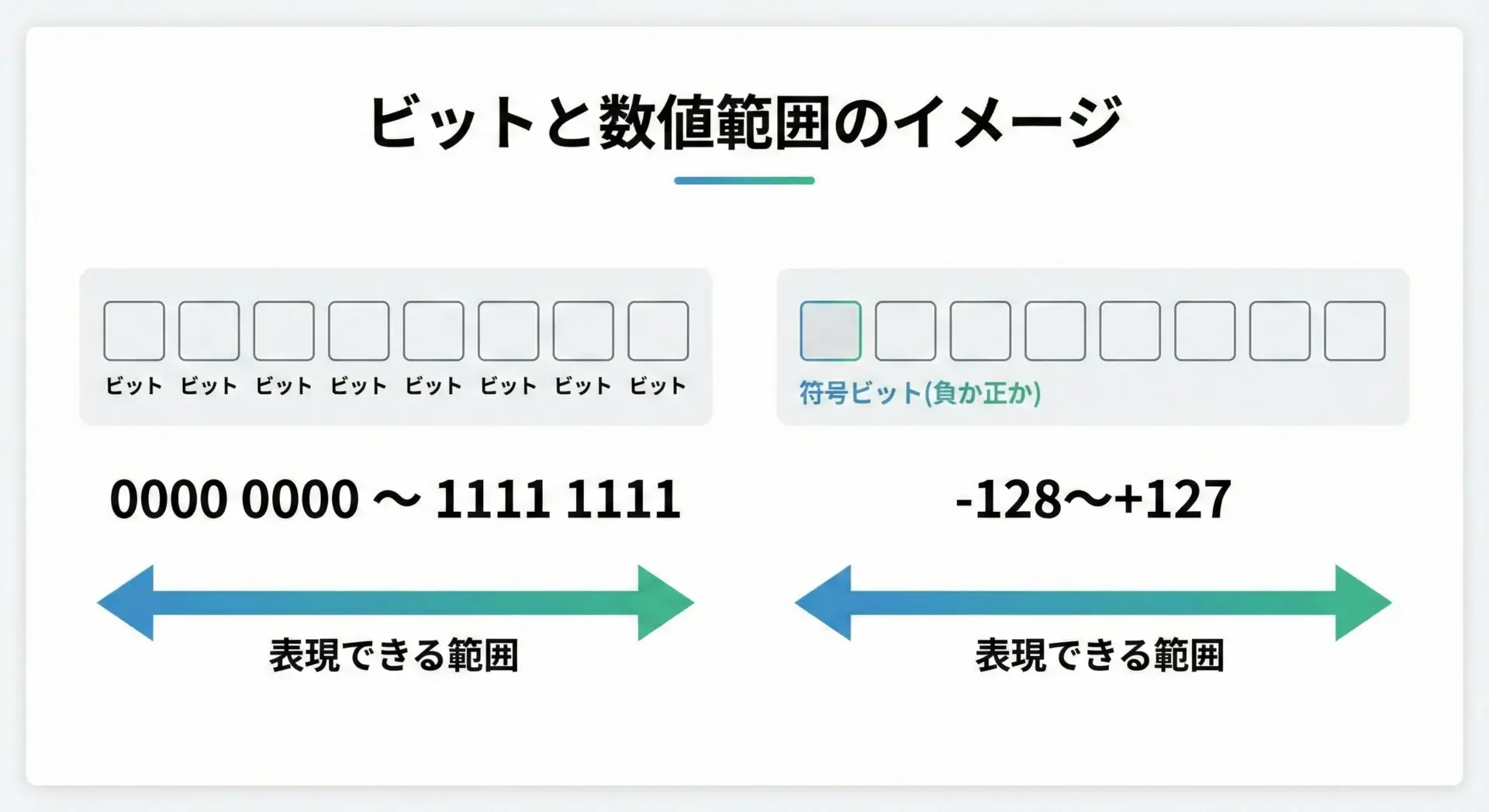
コンピュータは、数値をビット(bit)と呼ばれる0か1の箱の並びで表現します。
例えば8ビットなら全部で256通りの組み合わせしかありません。
そのため、表現できる数の種類が有限になり、当然最小値と最大値が決まります。
代表的な整数型を整理すると、次のようになります。
| 型の例 | ビット数 | 代表的な範囲の目安(2の補数整数) |
|---|---|---|
| 8ビット符号付き | 8ビット | -128 ~ +127 |
| 16ビット符号付き | 16ビット | -32768 ~ +32767 |
| 32ビット符号付き(int) | 32ビット | 約 -2.1×10^9 ~ +2.1×10^9 |
| 64ビット符号付き(long long など) | 64ビット | 約 -9.2×10^18 ~ +9.2×10^18 |
このように、型ごとに表現可能な範囲が決まっていることが、オーバーフローとアンダーフローの出発点になります。
オーバーフローとは何か
オーバーフローの直感的イメージ
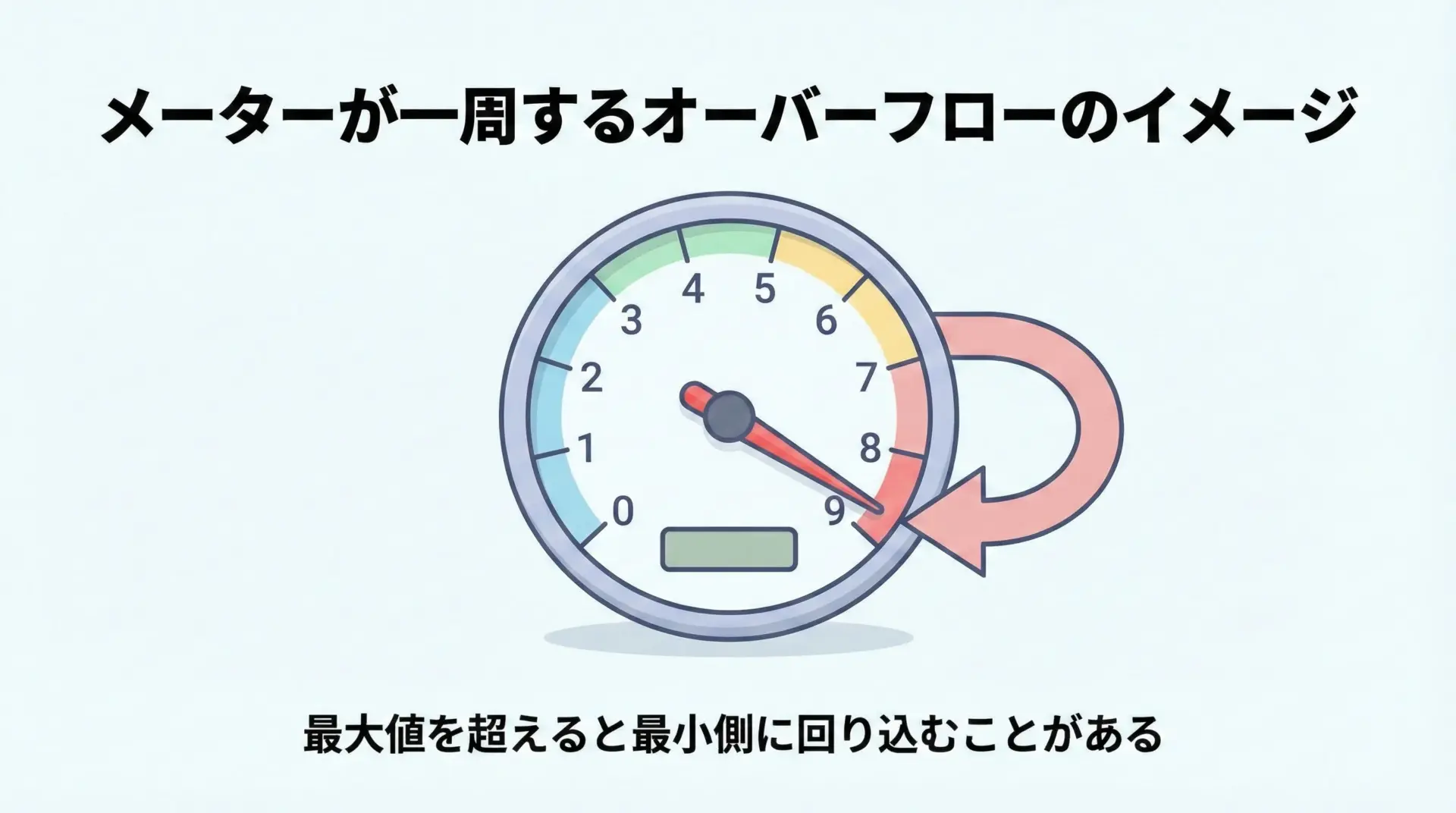
オーバーフローとは、「表現できる最大値を超えた結果を保存しようとしたときに起きる不具合」です。
たとえるなら、0〜9までしか表示できないメーターで「9の次」に1増やすと、10ではなく0に戻ってしまうイメージです。
整数の世界では、典型的に次のような動作になります。
- 最大値 + 1 → 最小値に「回り込む」
- 最小値 – 1 → 最大値に「回り込む」
この「回り込み」が、プログラムのバグの原因になりやすいポイントです。
C言語の整数オーバーフローの例
8ビット相当のオーバーフローを観察する
ここでは、実際の環境に依存しますが、signed charを使うことで、8ビット相当のオーバーフローを観察できます。
#include <stdio.h>
int main(void) {
// signed char は多くの処理系で -128〜127 を表現できることが多い
signed char max = 127;
signed char min = -128;
printf("max = %d\n", max);
printf("max + 1 = %d\n", (signed char)(max + 1)); // オーバーフローの例
printf("min = %d\n", min);
printf("min - 1 = %d\n", (signed char)(min - 1)); // 逆方向のオーバーフローの例
return 0;
}max = 127
max + 1 = -128
min = -128
min - 1 = 127この例では、127に1を足すと-128になり、-128から1を引くと127になっています。
最大値を超えると、最小値側に回り込んでしまう典型的なオーバーフローの例です。
注意点: C言語規格上は「未定義動作」
C言語の規格では、signedの整数オーバーフローは未定義動作とされています。
つまり、コンパイラや環境によって結果が異なってもよいことになっており、「オーバーフローが起きないように書くこと」が前提です。
実務では、次のような対策がよく用いられます。
- 計算の前に、結果が範囲を超えないかチェックする
- 余裕を持って、より大きな型(int → long long など)を使う
- 安全な演算関数(オーバーフロー検出付き)を利用する
アンダーフローとは何か
アンダーフローの直感的イメージ
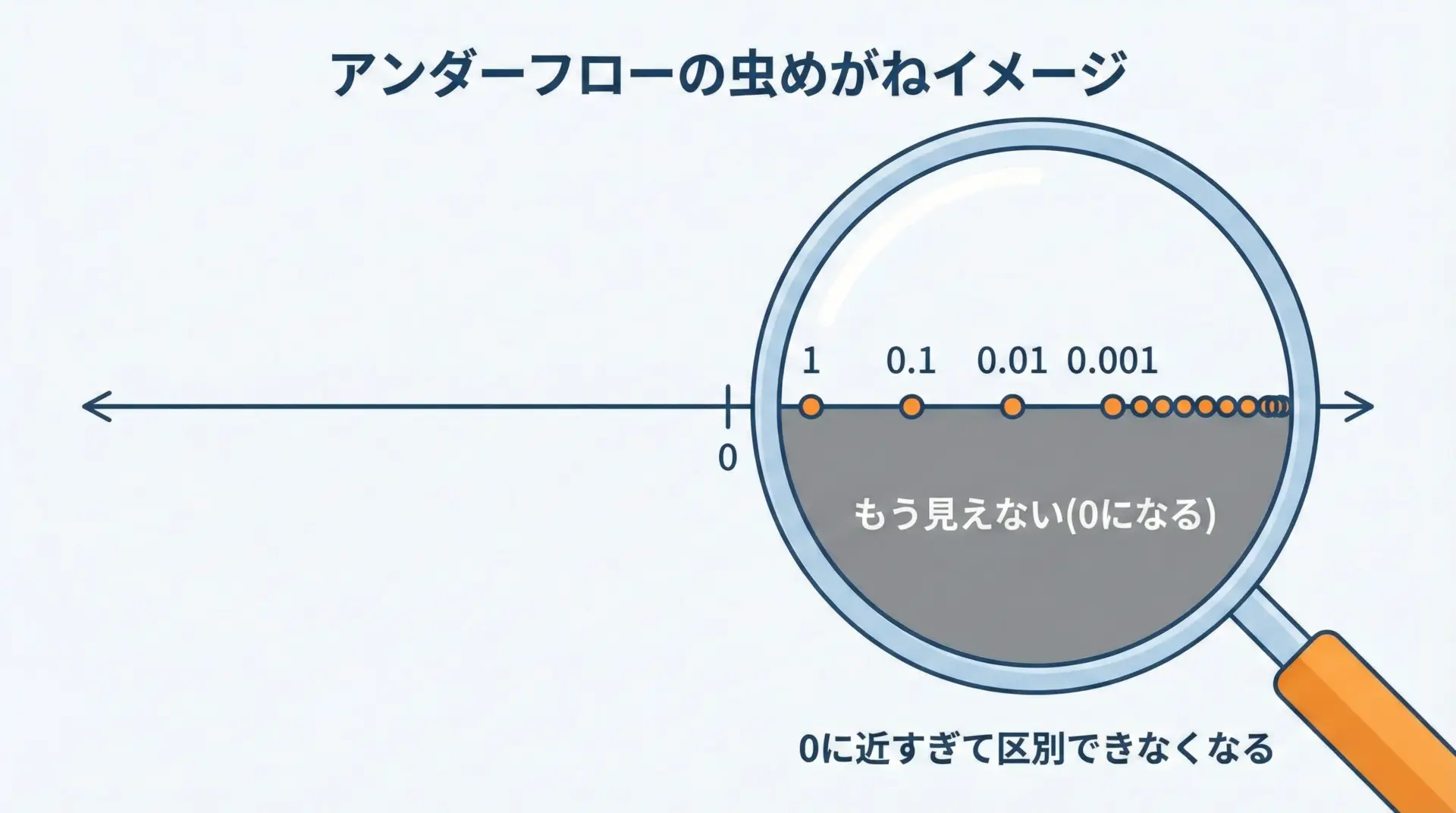
アンダーフローは、「表現できる最小の絶対値よりも小さい結果になったときに、その値を0などに丸めてしまう現象」です。
特に浮動小数点(小数を扱う型)で話題になります。
整数の場合も、「範囲外に小さくなりすぎる」という意味でアンダーフローという言い方をすることはありますが、多くの場合浮動小数点数の極小値を扱うときに使われる用語です。
浮動小数点の世界: double型の例
浮動小数点の表現範囲のイメージ
代表的な浮動小数点型(double)の範囲をざっくり表にすると次のようになります。
| 型 | おおよその範囲(正の値) | 説明 |
|---|---|---|
| double(正規化数) | 約 2.2×10^-308 ~ 1.8×10^308 | 通常の精度で扱える範囲 |
| double(非正規化数) | 約 5.0×10^-324 ~ 2.2×10^-308 | 精度を落として0に近い値を表す範囲 |
| 0 | 0 | それより小さい絶対値は区別できず0になる |
絶対値が約 5.0×10^-324 より小さい数は、double では表現できないため、計算の結果としては0になってしまいます。
これが典型的なアンダーフローです。
C言語でのアンダーフローの例
#include <stdio.h>
#include <float.h> // DBL_MIN, DBL_TRUE_MIN などの定義
int main(void) {
double x = DBL_MIN; // 正規化数としての最小の正の値
double y = DBL_TRUE_MIN; // 非正規化数としての最小の正の値(C11以降)
printf("DBL_MIN = %.17e\n", DBL_MIN);
printf("DBL_TRUE_MIN = %.17e\n", DBL_TRUE_MIN);
// どんどん2で割っていき、いつ0になるか確認する
double v = DBL_TRUE_MIN;
printf("start v = %.17e\n", v);
v = v / 2.0;
printf("v/2 = %.17e\n", v); // 多くの環境で 0.0 になる(アンダーフロー)
return 0;
}DBL_MIN = 2.2250738585072014e-308
DBL_TRUE_MIN = 4.9406564584124654e-324
start v = 4.9406564584124654e-324
v/2 = 0.0000000000000000e+00DBL_TRUE_MIN をさらに2で割っても、本来の数学的な値は 2.47…×10^-324 ですが、double では表現できないため 0 になります。
これが浮動小数点におけるアンダーフローです。
アンダーフローが問題になる場面
アンダーフローは、「非常に小さい値」を使う科学技術計算や物理シミュレーションなどで問題になることがあります。
例えば次のような場面です。
- 確率が非常に小さい事象を扱う統計計算
- 非常に小さい時間刻みでのシミュレーション
- 指数関数の計算で指数が大きな負の値になる場合
こうしたとき、理論上は0ではないのに、計算機上は0として扱われてしまうことで、計算結果が大きく変わってしまうことがあります。
整数と浮動小数点のオーバーフロー/アンダーフローの違い
ざっくり比較しておきましょう
| 種類 | 対象 | どんなときに起きるか | 典型的な挙動 |
|---|---|---|---|
| 整数オーバーフロー | int など | 最大値を超える計算 | 値が回り込み(別の値になる)、Cでは未定義動作 |
| 整数アンダーフロー | int など | 最小値より小さくなる計算 | 反対側の最大値に回り込むなど(環境依存) |
| 浮動小数点オーバーフロー | float/double | 絶対値が最大表現値を超える | 無限大(+∞, -∞)になることが多い |
| 浮動小数点アンダーフロー | float/double | 絶対値が最小表現値より小さい | 0に丸められる(または非正規化数を経て0へ) |
整数のオーバーフローは「値の回り込み」によるバグが問題になり、浮動小数点のアンダーフローは「本当は0でないのに0になる」ことが問題になります。
オーバーフローとアンダーフローを避ける考え方
1. 「安全な範囲」を意識して設計する
プログラムを書くときには、「この変数は、どのくらいの範囲の値をとりうるか」を最初に想定しておくことが重要です。
そのうえで、次のような工夫をします。
- 桁あふれしそうなら、より大きな型を選ぶ
- 32ビットの
intでは足りないなら64ビットのlong longを使う
- 32ビットの
- 計算順序を工夫して、極端に大きい/小さい値を避ける
- ループ回数や入力値に上限を設ける
2. 計算前にチェックを入れる
整数演算でオーバーフローが起きそうなときには、あらかじめ条件分岐でチェックする方法があります。
簡単な例を見てみます。
#include <stdio.h>
#include <limits.h> // INT_MAX, INT_MIN など
// a + b が int の範囲に収まるかをチェックしてから計算する関数
int safe_add_int(int a, int b, int *overflow) {
*overflow = 0;
// a > 0 かつ b > 0 のとき: a > INT_MAX - b ならオーバーフロー
if (a > 0 && b > 0 && a > INT_MAX - b) {
*overflow = 1;
return 0;
}
// a < 0 かつ b < 0 のとき: a < INT_MIN - b ならオーバーフロー
if (a < 0 && b < 0 && a < INT_MIN - b) {
*overflow = 1;
return 0;
}
return a + b;
}
int main(void) {
int overflow;
int a = INT_MAX;
int b = 1;
int result = safe_add_int(a, b, &overflow);
if (overflow) {
printf("オーバーフローの可能性があるため、計算を中止しました。\n");
} else {
printf("計算結果: %d\n", result);
}
return 0;
}このように、境界値を使って事前に判定することで、安全な範囲内だけで計算することができます。
3. 浮動小数点では「スケーリング」を考える
浮動小数点のアンダーフローやオーバーフローを避けるには、値のスケール(桁)を調整するという考え方がよく使われます。
例えば、非常に大きな数Aと非常に小さな数Bの積A * Bを計算するとき、直接計算するとオーバーフローやアンダーフローが起きることがあります。
この場合、次のような工夫が考えられます。
- 対数(ログ)を使って、
log(A * B) = log(A) + log(B)の形に変換する - 途中計算で使う単位を変える(メートルをキロメートルにするなど)
こうした数学的な工夫も、数値計算では非常に重要です。
よくある誤解と注意点
「大きい型を使えば安心」は半分正しくて半分間違い
64ビット整数やdoubleを使えば、多くのケースでオーバーフローやアンダーフローを避けやすくなります。
しかし、理論的にはどれだけビット数を増やしても、いずれ上限や下限にぶつかる可能性は残ります。
- 長期間のカウンタ(例: サーバの累積アクセス数)
- 大規模なシミュレーション(繰り返し回数が膨大)
- 高精度が求められる科学技術計算
このような場面では、型を大きくするだけでなく、アルゴリズム設計そのものから慎重に考える必要があることに注意してください。
「テストで動いていれば大丈夫」は危険
オーバーフローやアンダーフローは、「ある特定の入力値でだけ」起きることが多いため、少ないテストケースでは発見しづらい問題です。
テストが通っていても、次のような対策を合わせて検討することが重要です。
- 静的解析ツールで潜在的なオーバーフローを検出する
- 入力値の制限を仕様として明記する
- 範囲外の値が来たときの処理(エラーにするなど)を用意しておく
まとめ
オーバーフローとアンダーフローは、コンピュータが有限のビット数で数を表現していることから必然的に生じる現象です。
整数では主にオーバーフローによる「値の回り込み」が問題になり、浮動小数点では極端に大きい値や小さい値が「無限大」や「0」に丸められてしまうことが問題になります。
安全なプログラムを書くためには、扱う値の範囲を意識し、必要に応じて型やアルゴリズムを選び、境界値付近での挙動を意識して設計することが大切です。
今回の内容を踏まえ、自分のコードの中でどこにオーバーフローやアンダーフローのリスクが潜んでいるか、意識して見直してみてください。

