固定小数点数は、組み込み機器やリアルタイム処理、金融計算などで今も広く使われている数値表現です。
本記事では、固定小数点数の基本的な仕組みから、浮動小数点数との違い、メリット・デメリット、そして簡単なC言語での実装例までを、できるだけ直感的に理解できるように解説します。
固定小数点数とは何か
固定小数点数の基本イメージ

固定小数点数とは、その名の通り小数点の位置があらかじめ固定されている数値表現のことです。
コンピュータ内部では整数として値を持ち、どこに小数点があるかを「約束事」として決めておき、その約束に基づいて値を解釈します。
具体例でイメージする
例えば、次のようなルールを決めるとします。
- 「整数値を100倍したものを内部表現として保存する」
この場合、内部に保存する値と、実際の数値の関係は次のようになります。
内部の整数値 → 実際の数値
| 内部の値(int) | 実際の値(固定小数点として解釈) |
|---|---|
| 123 | 1.23 |
| 100 | 1.00 |
| 5 | 0.05 |
| -250 | -2.50 |
このように「どこに小数点があるか」は値の中には書かれておらず、扱う側のルールで決めるのが固定小数点数の大きな特徴です。
固定小数点と浮動小数点の違い
浮動小数点数とどう違うのか
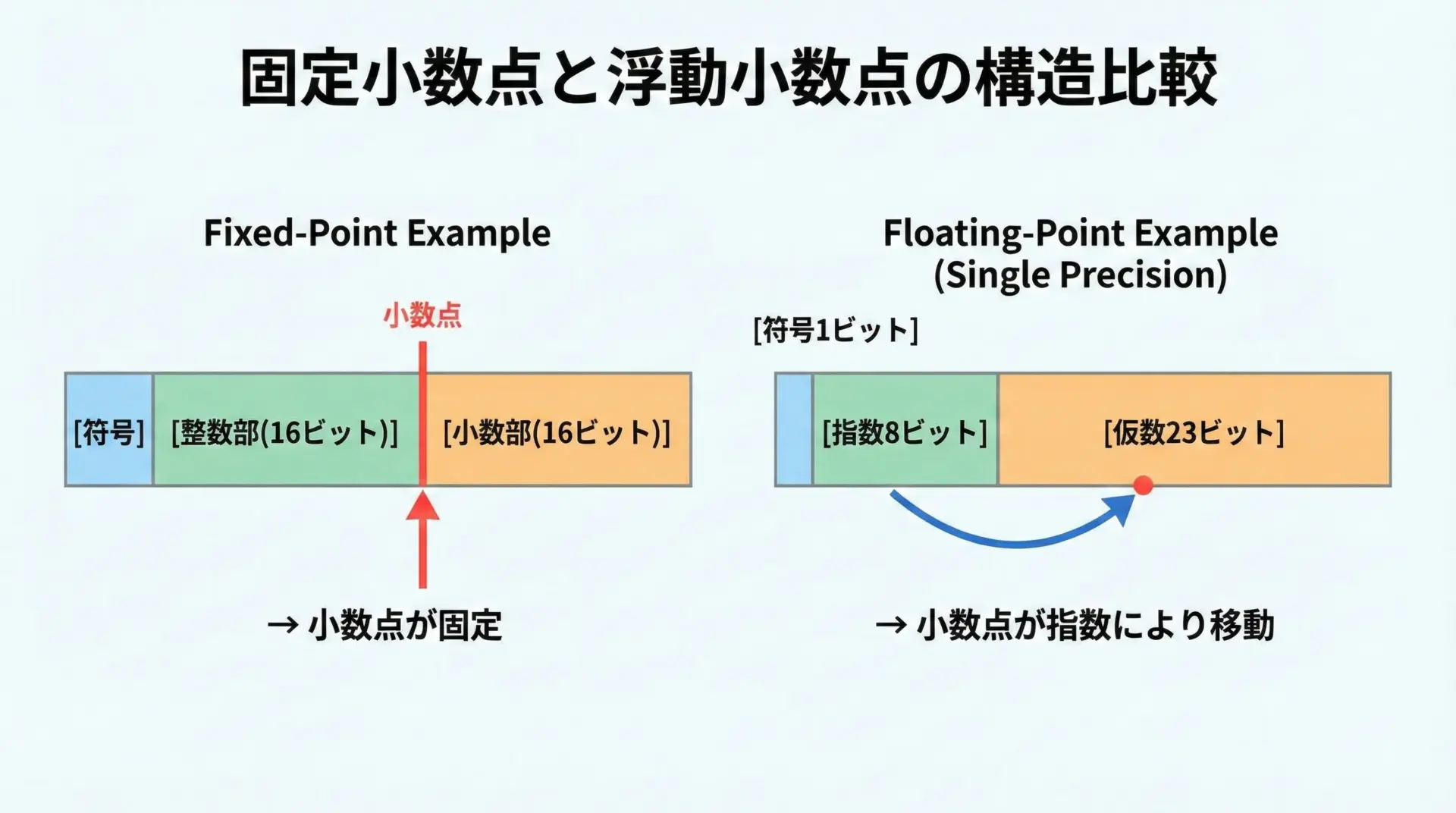
浮動小数点数(例: IEEE754のfloatやdouble)は、「指数部」と「仮数部」に分かれており、小数点の位置が指数によって「動く」ため、非常に広い範囲の数を表現できます。
一方、固定小数点数は小数点の位置が不動であり、表現できる範囲は限られますが、小数点以下の刻みが一定という特徴を持ちます。
特徴の比較
次の表で、主な違いを整理します。
| 項目 | 固定小数点数 | 浮動小数点数 |
|---|---|---|
| 小数点の位置 | 固定(事前に決める) | 可変(指数で動く) |
| 表現できる範囲 | 比較的狭い | 非常に広い |
| 刻み幅(最小単位) | 一定 | 値の大きさによって変化 |
| 実装の複雑さ | 比較的単純(整数演算ベース) | 複雑(専用ハードウェアがあることが多い) |
| 計算速度(組み込みなど) | 場合によっては高速 | ハードウェア依存 |
| 代表的な用途 | 金融計算、音声処理、組み込み制御など | 科学技術計算、3Dグラフィックスなど |
| 丸め誤差の性質 | 一定刻みの誤差で直感的に扱いやすい | 値によって誤差の大きさや方向が変わりやすい |
「範囲と柔軟性」は浮動小数点、「シンプルさと一定刻み」は固定小数点という対比で覚えると理解しやすくなります。
固定小数点の表現方法
Q形式(Q-format)とは
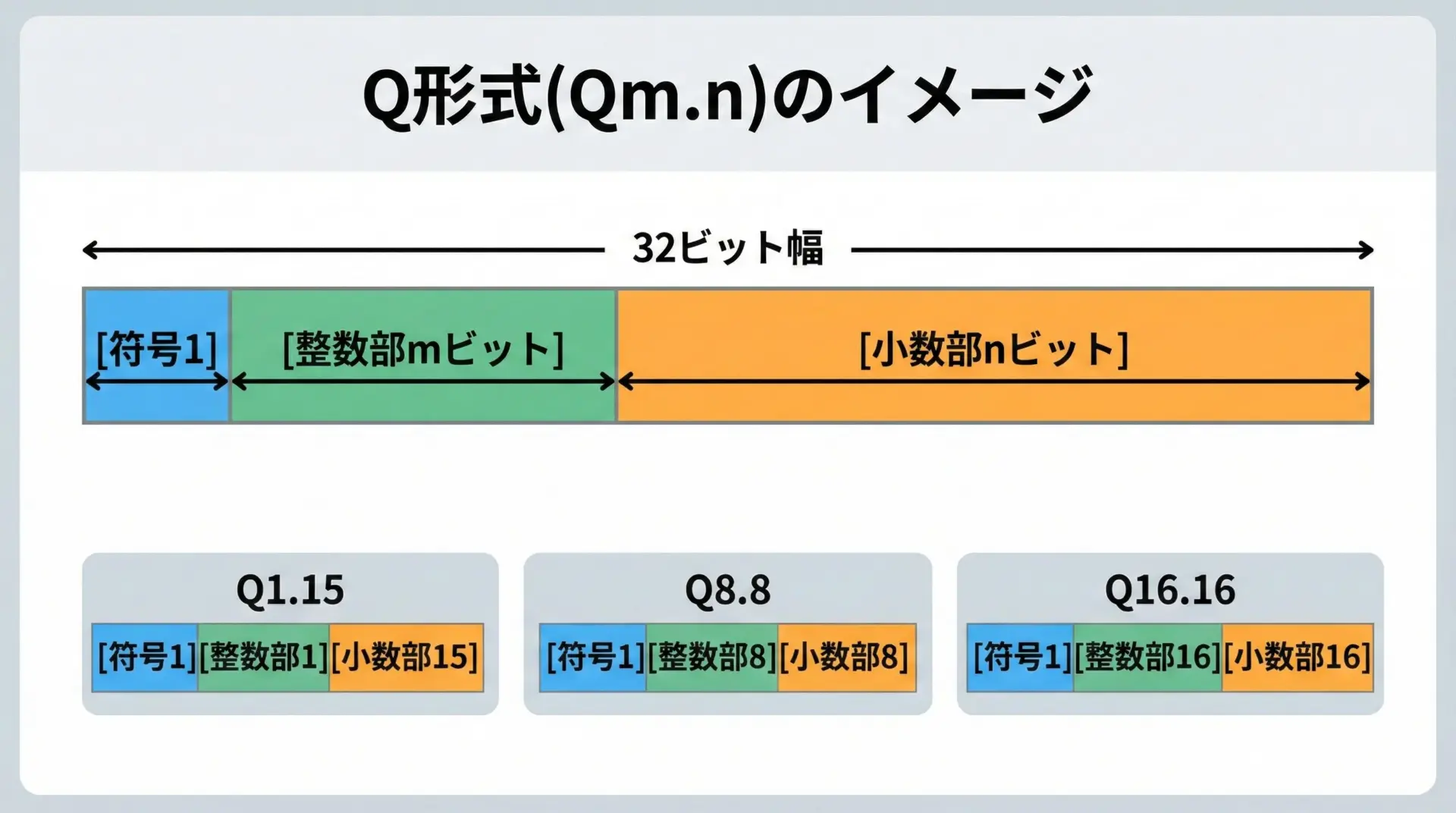
固定小数点数を表すときによく使われる表記にQ形式(Qm.n)があります。
Qm.nは、次のような意味を持ちます。
- 全体のビット幅を
m + n + 1ビットとする(先頭1ビットは符号) - 符号付きで、整数部がmビット、小数部がnビット
例えばQ1.15は、16ビット幅で
- 1ビット: 符号と整数部(0か1)
- 15ビット: 小数部
という構成になります。
Q形式の具体例(Q1.15)

Q1.15では、小数部は2進数の重み1/2, 1/4, 1/8, …で表されます。
符号付き16ビット整数の値をxとすると、実数としての値は
- 実数値 = x / 2^15
となります。
ここで2^15 = 32768です。
固定小数点の範囲と精度
範囲の求め方(Q1.15の例)
16ビットの符号付き整数は-32768 ~ 32767を表現できます。
Q1.15では実数値は整数値 / 32768なので、表現できるおおよその範囲は次のようになります。
- 最小値: -32768 / 32768 = -1.0
- 最大値: 32767 / 32768 ≒ 0.9999695
したがって、Q1.15はほぼ[-1.0, 1.0)の範囲を、約3.05×10^-5刻みで表現できる形式といえます。
刻み幅(最小単位)の考え方
Qm.n形式では、実数値の最小刻み幅は1 / 2^nになります。
例えば次のようになります。
| 形式 | 小数部ビット数 n | 刻み幅(最小単位) | およその10進数 |
|---|---|---|---|
| Q1.15 | 15 | 1 / 32768 | 約 0.0000305 |
| Q8.8 | 8 | 1 / 256 | 約 0.0039 |
| Q16.16 | 16 | 1 / 65536 | 約 0.0000153 |
小数部のビット数を増やすほど精度は上がりますが、それだけ整数部に使えるビットが減り、表現できる最大値が小さくなる点に注意が必要です。
固定小数点での四則演算の考え方
加算・減算はそのまま
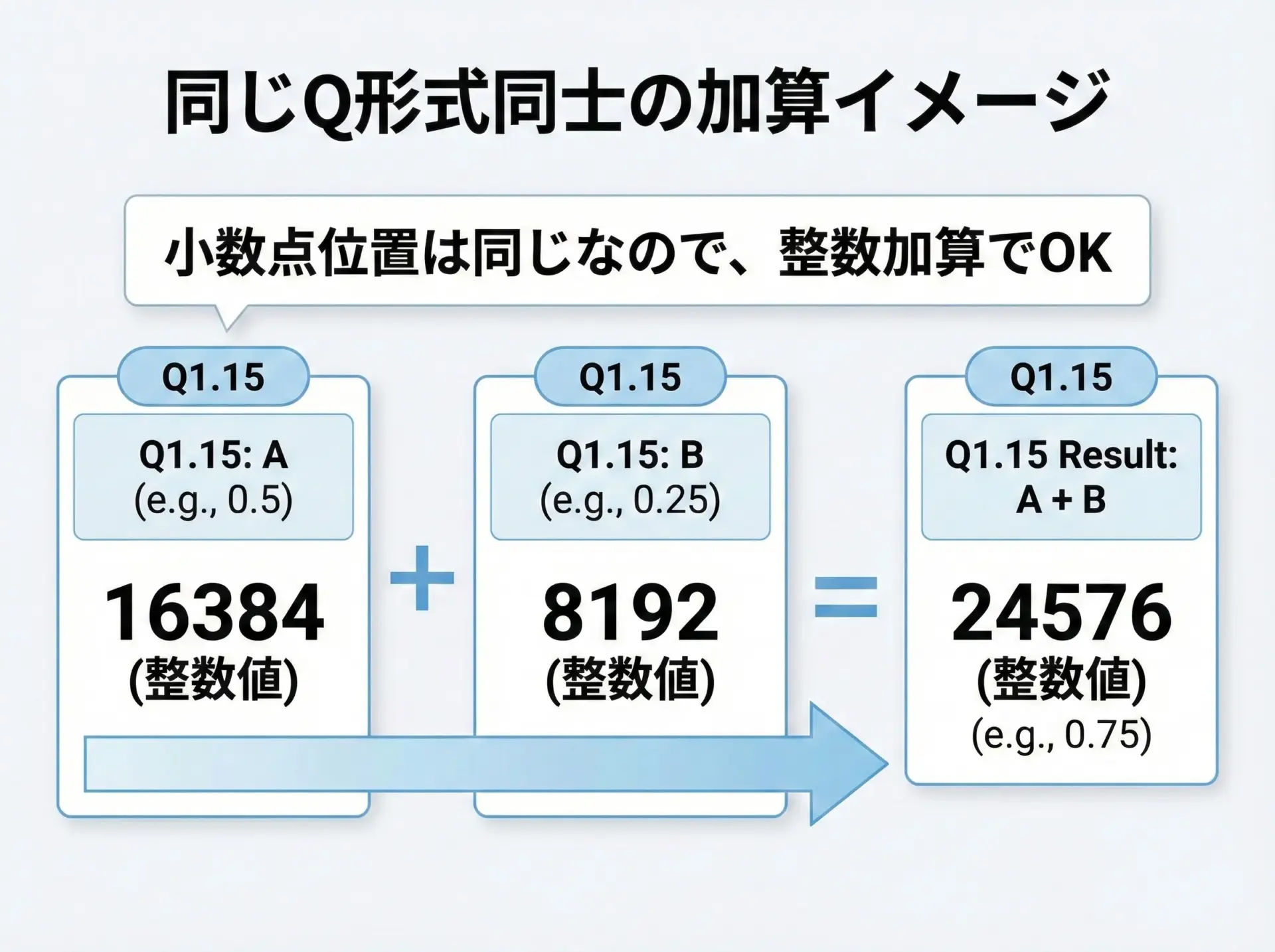
同じQ形式同士の加算・減算は、単純に整数同士の加算・減算として行えます。
これは、小数点の位置が両方とも同じであるためです。
ただし、結果が表現可能な範囲を超えた場合はオーバーフローが発生するため、注意して設計する必要があります。
乗算・除算ではスケーリングが必要
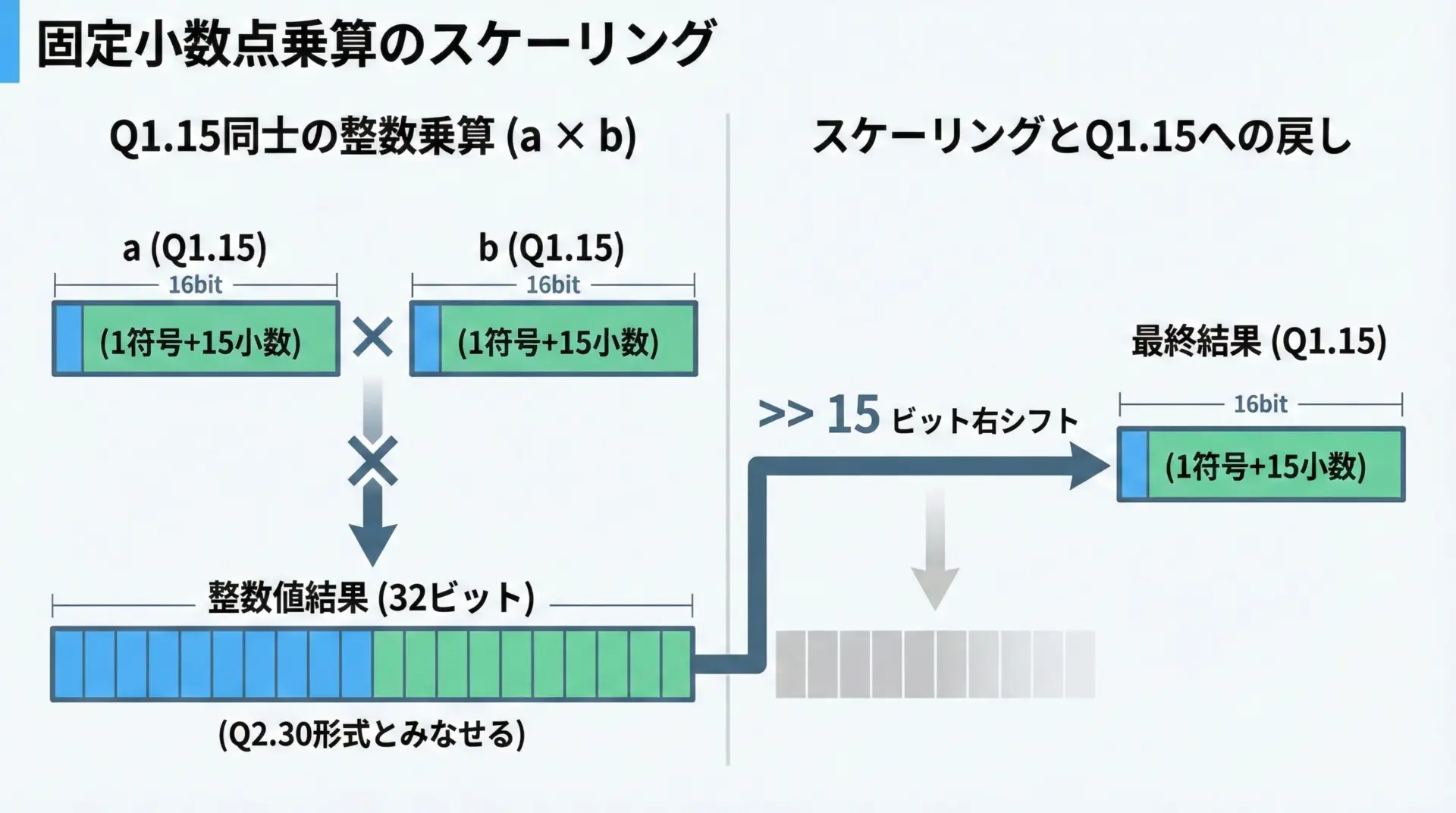
乗算の場合、Q1.15の値を例にすると次のような関係になります。
- 実数値a = A / 2^15
- 実数値b = B / 2^15
- 実数値(a×b) = (A×B) / 2^30
このままだと、小数部が30ビット分あることになってしまい、元のQ1.15形式とはスケールが合いません。
そこで、結果(A×B)を右に15ビットシフトして、再び2^15で割った形に戻すという操作を行います。
- 固定小数点としての結果C = (A×B) >> 15
このように、乗算や除算ではシフト操作によるスケーリング調整が重要なポイントになります。
C言語で固定小数点を扱う簡単な例
Q1.15形式の基本的な実装
ここでは、16ビットのQ1.15形式を用いて、実数との相互変換や加算・乗算を行うサンプルコードを示します。
#include <stdio.h>
#include <stdint.h>
/*
* Q1.15 固定小数点のサンプル実装
* - 内部表現: int16_t (符号付き16ビット整数)
* - 実数値 = 内部値 / 2^15
*/
#define Q15_FRACTION_BITS 15
#define Q15_SCALE (1 << Q15_FRACTION_BITS) // 2^15 = 32768
// double から Q1.15 へ変換
int16_t double_to_q15(double x) {
// 表現可能範囲を超えないようにクリップ
if (x > 0.999969482421875) { // 32767 / 32768
x = 0.999969482421875;
}
if (x < -1.0) {
x = -1.0;
}
// スケールを掛けて丸めてから整数に変換
int32_t temp = (int32_t)(x * Q15_SCALE);
return (int16_t)temp;
}
// Q1.15 から double へ変換
double q15_to_double(int16_t q) {
return (double)q / (double)Q15_SCALE;
}
// Q1.15 同士の加算(単純な整数加算)
// オーバーフローには注意が必要(ここでは簡略化のため未対策)
int16_t q15_add(int16_t a, int16_t b) {
int32_t temp = (int32_t)a + (int32_t)b;
// 16ビットに収まる範囲にクリップするのが安全
if (temp > 32767) temp = 32767;
if (temp < -32768) temp = -32768;
return (int16_t)temp;
}
// Q1.15 同士の乗算
int16_t q15_mul(int16_t a, int16_t b) {
// まず 32ビットで掛け算してオーバーフローを避ける
int32_t temp = (int32_t)a * (int32_t)b; // 最大で約 1e9 程度
// Q1.15 × Q1.15 = Q2.30 相当なので、15ビット右シフトして Q1.15 に戻す
temp = temp >> Q15_FRACTION_BITS;
// 16ビットに収まるようにクリップ
if (temp > 32767) temp = 32767;
if (temp < -32768) temp = -32768;
return (int16_t)temp;
}
int main(void) {
// 実数をQ1.15に変換してから演算し、結果をまた実数に戻す例
double a_real = 0.5; // 0.5
double b_real = -0.25; // -0.25
// 実数 → 固定小数点
int16_t a_q15 = double_to_q15(a_real);
int16_t b_q15 = double_to_q15(b_real);
// 加算と乗算
int16_t sum_q15 = q15_add(a_q15, b_q15);
int16_t mul_q15 = q15_mul(a_q15, b_q15);
// 固定小数点 → 実数
double sum_real = q15_to_double(sum_q15);
double mul_real = q15_to_double(mul_q15);
printf("a_real = %f, b_real = %f\n", a_real, b_real);
printf("a_q15 = %d, b_q15 = %d\n", a_q15, b_q15);
printf("sum = %f (Q15=%d)\n", sum_real, sum_q15);
printf("mul = %f (Q15=%d)\n", mul_real, mul_q15);
return 0;
}想定される実行結果の一例は次のようになります。
(環境や丸めにより若干異なる場合があります)
a_real = 0.500000, b_real = -0.250000
a_q15 = 16384, b_q15 = -8192
sum = 0.250000 (Q15=8192)
mul = -0.125000 (Q15=-4096)ここで、内部ではすべて整数演算で処理されていることがポイントです。
整数演算は多くのCPUで高速に実行できるため、浮動小数点演算ユニットを持たない組み込みCPUなどでの高速な数値処理に適しています。
固定小数点を使うメリットとデメリット
固定小数点のメリット
固定小数点数には、次のようなメリットがあります。
1つ目は実装が比較的シンプルで、整数演算だけで完結する点です。
専用の浮動小数点ユニットがないCPUでも、効率よく数値計算が行えます。
2つ目は丸め誤差の挙動が直感的であることです。
刻み幅が一定なため、「必ず0.01刻みで扱いたい」「絶対に0.1のような金額の単位を狂わせたくない」といった用途に向いています。
金融計算やポイント計算などでよく採用されます。
3つ目は再現性の高い計算結果を得やすい点です。
環境差の少ない整数演算を使うことで、プラットフォーム間で同じ計算結果を得やすくなります。
固定小数点のデメリット
一方で、固定小数点数には次のようなデメリットもあります。
1つ目は表現できる範囲が狭いことです。
整数部と小数部が固定のビット幅で分けられているため、大きな値と非常に小さな値の両方を同時に高精度で扱うことは苦手です。
2つ目は乗算や除算でスケーリング調整が必要なことです。
ビットシフトやクリッピングの処理をきちんと設計しないと、簡単にオーバーフローや精度劣化を招いてしまいます。
3つ目は形式の選択(Q1.15なのかQ8.8なのかなど)を誤ると、後から変更が難しいという設計上の難しさです。
どの範囲の値をどれくらいの精度で扱うのかを、事前に見積もる必要があります。
浮動小数点とどちらを選ぶべきか
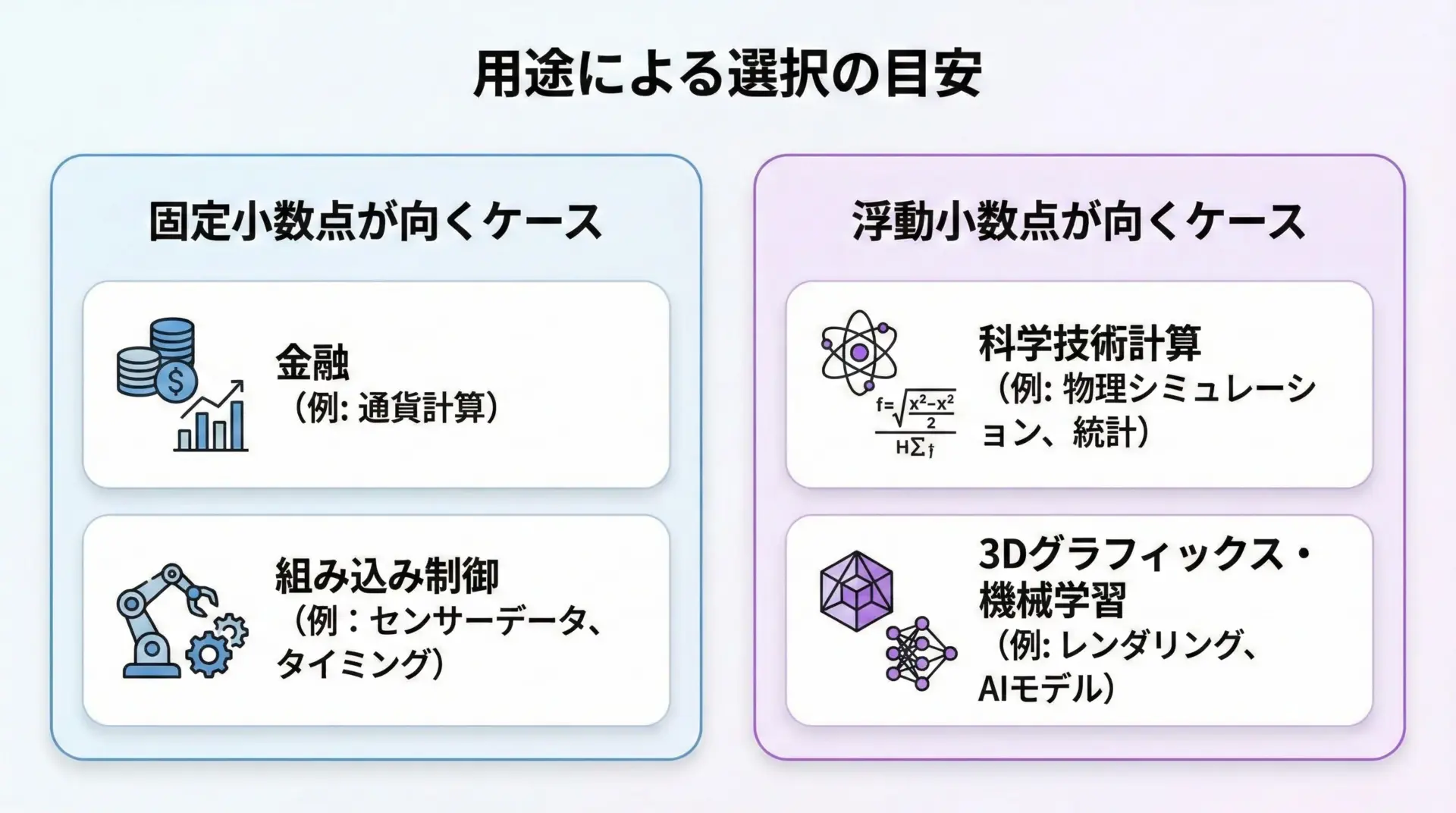
用途によって、固定小数点と浮動小数点のどちらを使うべきかは変わります。
固定小数点が向いているケースとしては、次のようなものがあります。
- マイコンなどで浮動小数点ユニットが貧弱、あるいは存在しない場合
- 金額やポイントなど、単位刻みが明確で、その刻みから外れた値を扱いたくない場合
- 音声信号やセンサ値など、扱う範囲がある程度決まっているリアルタイム処理
一方、浮動小数点が向いているケースは次のようなものです。
- 非常に広いダイナミックレンジ(極小値から極大値まで)を扱う必要がある科学技術計算
- 3Dグラフィックスや物理シミュレーションなど、モデルのスケールが大きく変化する処理
- 機械学習や統計計算など、多種多様なスケールのデータを扱う処理
「どの程度の範囲と精度が本当に必要か」を冷静に見積もり、固定小数点か浮動小数点かを選択することが重要です。
まとめ
固定小数点数は、「小数点の位置をあらかじめ決めて、内部では整数として扱う」表現方式です。
浮動小数点に比べて表現範囲は狭い一方で、刻み幅が一定で直感的に扱いやすく、整数演算のみで高速に処理できるという利点があります。
特に、マイコンや金融計算、リアルタイム信号処理などでは今も重要な役割を担っています。
自分の用途に必要な範囲と精度を見積もり、適切なQ形式を選びつつ、乗算時のスケーリングやオーバーフロー対策を意識することで、固定小数点を効果的に活用できるようになります。