グレイコードとは？基本概念から実用な応用までわかりやすく解説

2025年10月30日2026年1月14日

その他

グレイコードは、デジタル信号が変化するときに誤りを起こしにくくするために生まれた特別な2進数表現です。

本記事では、グレイコードの基本概念から、よく使われる変換方法、プログラム例、エンコーダなどでの実用的な応用までを、図解を交えながら順番に解説します。

通常の2進数との違いを理解することで、なぜハードウェア設計や誤り低減の場面で重宝されるのかが見えてきます。

目次 [ close ]

グレイコードとは何か

グレイコードの基本的な考え方

グレイコード(Gray code)は、連続するコード同士が必ず1ビットだけ異なるように並んだ2進数列のことです。

英語では「Reflected Binary Code」(反射2進コード)とも呼ばれます。

通常の2進数では、ある値から次の値に変化するときに複数ビットが同時に変わることがありますが、グレイコードでは必ず1ビットだけが変化します。

この性質によって、次に説明するような誤り低減やノイズ耐性の向上といった利点が得られます。

なぜ1ビットだけ変化することが重要なのか

デジタル回路では、理論上はビットが同時に変化することになっていても、物理的には微小な時間差が生じます。

すると、例えば3ビットが同時に変わるはずの瞬間に、

1ビット目だけ変わった状態
2ビット目と3ビット目だけ変わった中途半端な状態

といった一時的で不正確なビットパターンが観測されることがあります。

これがセンサ出力やアドレス線に使われていると、本来とはまったく違う値として解釈されてしまう危険があります。

グレイコードでは連続する値で1ビットしか変化しないため、もしタイミングのズレで一時的な誤読が起きても、

正しい値
その1つ前(または1つ後)の値

のどちらかにしかなりません。

誤差が「隣接する値」に限定されるので、大きな飛び誤差を避けられるのが大きなポイントです。

2進数とグレイコードの比較

3ビットの場合の一覧

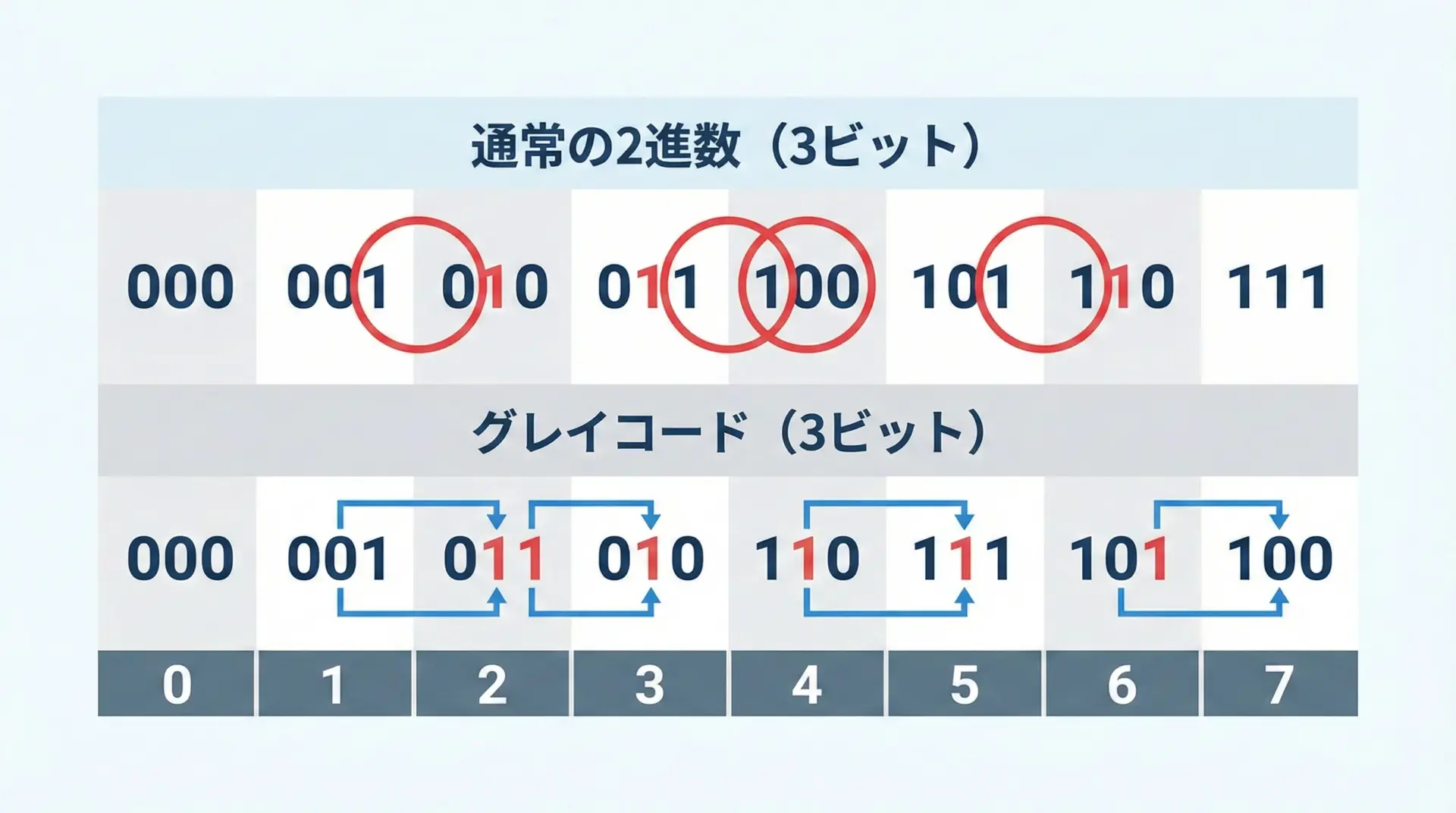
3ビットの通常の2進数と、3ビットのグレイコードを並べて比べてみます。

10進数	通常の2進数	グレイコード
0	000	000
1	001	001
2	010	011
3	011	010
4	100	110
5	101	111
6	110	101
7	111	100

この表を上から順に見ていくと、グレイコードの列ではどこを見ても隣同士が1ビットの違いになっています。

例えば、

3(010)から4(110)に移るときは最上位ビットだけが変化
6(101)から7(100)に移るときは下位ビットだけが変化

という具合です。

一方、通常の2進数では、3(011)から4(100)に変わるときのように、3ビットすべてが同時に変化する箇所も存在します。

この違いが、ノイズやタイミングずれに対する強さの差につながります。

グレイコードの「反射」構成ルール

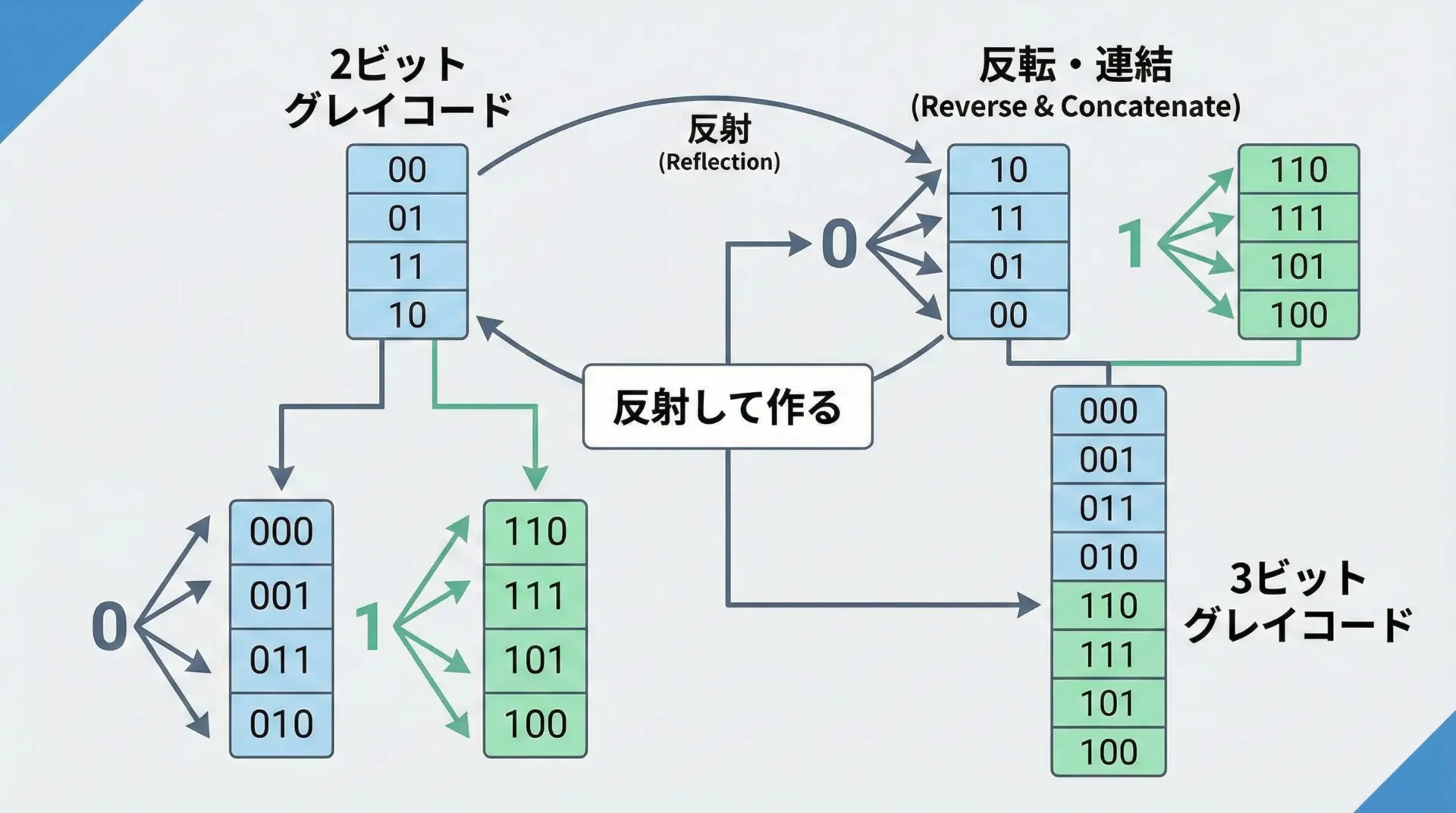
グレイコードは反射(reflection)というシンプルな手順で構成できます。

例えば、2ビットから3ビットに拡張するときは、次のように行います。

2ビットのグレイコード列を用意する
00, 01, 11, 10
これをそのまま上に書き、各コードの先頭に0を付ける
000, 001, 011, 010
2ビットの列を上下反転(反射)して下側に並べ、先頭に1を付ける
110, 111, 101, 100
上下をつなげると3ビットのグレイコード列になる
000, 001, 011, 010, 110, 111, 101, 100

このように、1ビット増やすごとに「上に0付き」「反転させて1付き」を連結するというルールで、任意ビット長のグレイコードが作れます。

2進数とグレイコードの相互変換

2進数からグレイコードへの変換

2進数のビット列をb、グレイコードをgと書くと、変換は次のルールで行えます。

最上位ビットはそのまま
g[n-1] = b[n-1]
それ以外のビットは、bの隣り合うビットの排他的論理和(XOR)
g[i] = b[i+1] XOR b[i]

例として、2進数1011(10進数で11)をグレイコードに変換してみます。

最上位ビット: g3 = b3 = 1
g2 = b3 XOR b2 = 1 XOR 0 = 1
g1 = b2 XOR b1 = 0 XOR 1 = 1
g0 = b1 XOR b0 = 1 XOR 1 = 0

よって、グレイコードは1110になります。

グレイコードから2進数への変換

逆に、グレイコードgから2進数bへの変換は、次のルールになります。

最上位ビットはそのまま
b[n-1] = g[n-1]
それ以外のビットは、上位ビットまでの2進数ビットとのXOR
b[i] = b[i+1] XOR g[i]

先ほどの例のg = 1110から2進数に戻してみます。

b3 = g3 = 1
b2 = b3 XOR g2 = 1 XOR 1 = 0
b1 = b2 XOR g1 = 0 XOR 1 = 1
b0 = b1 XOR g0 = 1 XOR 0 = 1

結果は1011となり、元の2進数に戻せました。

C言語によるグレイコード変換の実装例

2進数→グレイコード変換プログラム

グレイコードへの変換は、ビット演算を使うと非常に簡単に書けます。

よく知られている式はgray = n ^ (n >> 1)です。

C言語

#include <stdio.h>

// 10進整数nをグレイコードに変換する関数
// 返り値も整数ですが、ビットパターンがグレイコードになります
unsigned int binary_to_gray(unsigned int n) {
    // nを1ビット右シフトし、元のnとXORを取ることでグレイコードを生成
    return n ^ (n >> 1);
}

// ビット列を表示するヘルパー関数(上位ビットから表示)
void print_bits(unsigned int x, int bits) {
    for (int i = bits - 1; i >= 0; --i) {
        unsigned int mask = 1u << i;
        putchar((x & mask) ? '1' : '0');
    }
}

int main(void) {
    unsigned int n;

    // 0〜7までの数値について、2進数とグレイコードを表示
    for (n = 0; n < 8; ++n) {
        unsigned int g = binary_to_gray(n);

        printf("n = %u: ", n);
        printf("binary = ");
        print_bits(n, 3);    // 3ビットで表示
        printf(", gray = ");
        print_bits(g, 3);    // 3ビットで表示
        printf("\n");
    }

    return 0;
}

実行結果

n = 0: binary = 000, gray = 000
n = 1: binary = 001, gray = 001
n = 2: binary = 010, gray = 011
n = 3: binary = 011, gray = 010
n = 4: binary = 100, gray = 110
n = 5: binary = 101, gray = 111
n = 6: binary = 110, gray = 101
n = 7: binary = 111, gray = 100

この出力は、先ほど表で示した3ビットグレイコードの並びと一致しています。

グレイコード→2進数変換プログラム

グレイコードから2進数への復号も、ビット演算を用いて実装できます。

下のビットへ向かって順にXORを蓄積していく実装方法がよく使われます。

C言語

#include <stdio.h>

// グレイコードgを通常の2進数に変換する関数
unsigned int gray_to_binary(unsigned int g) {
    unsigned int b = 0;

    // gの最上位ビットから順に処理する方法もありますが、
    // ここではよく知られた「右に畳み込む」アルゴリズムを使います。
    //
    // gを右シフトしながらXORしていくと、最終的に通常の2進数になります。
    for (; g != 0; g >>= 1) {
        b ^= g;  // 現在のgをbにXORで折り重ねる
    }

    return b;
}

// ビット表示用(前と同じヘルパー関数)
void print_bits(unsigned int x, int bits) {
    for (int i = bits - 1; i >= 0; --i) {
        unsigned int mask = 1u << i;
        putchar((x & mask) ? '1' : '0');
    }
}

int main(void) {
    // 0〜7までのグレイコードを2進数に戻すデモ
    for (unsigned int gray = 0; gray < 8; ++gray) {
        unsigned int bin = gray_to_binary(gray);

        printf("gray = ");
        print_bits(gray, 3);
        printf(" -> binary = ");
        print_bits(bin, 3);
        printf(" (dec %u)\n", bin);
    }

    return 0;
}

実行結果

gray = 000 -> binary = 000 (dec 0)
gray = 001 -> binary = 001 (dec 1)
gray = 010 -> binary = 011 (dec 3)
gray = 011 -> binary = 010 (dec 2)
gray = 100 -> binary = 111 (dec 7)
gray = 101 -> binary = 110 (dec 6)
gray = 110 -> binary = 100 (dec 4)
gray = 111 -> binary = 101 (dec 5)

このように、2行程度のビット演算だけでグレイコードとの相互変換が行えるため、組み込みシステムでも広く利用されています。

グレイコードの主な応用例

回転エンコーダ・位置センサでの利用

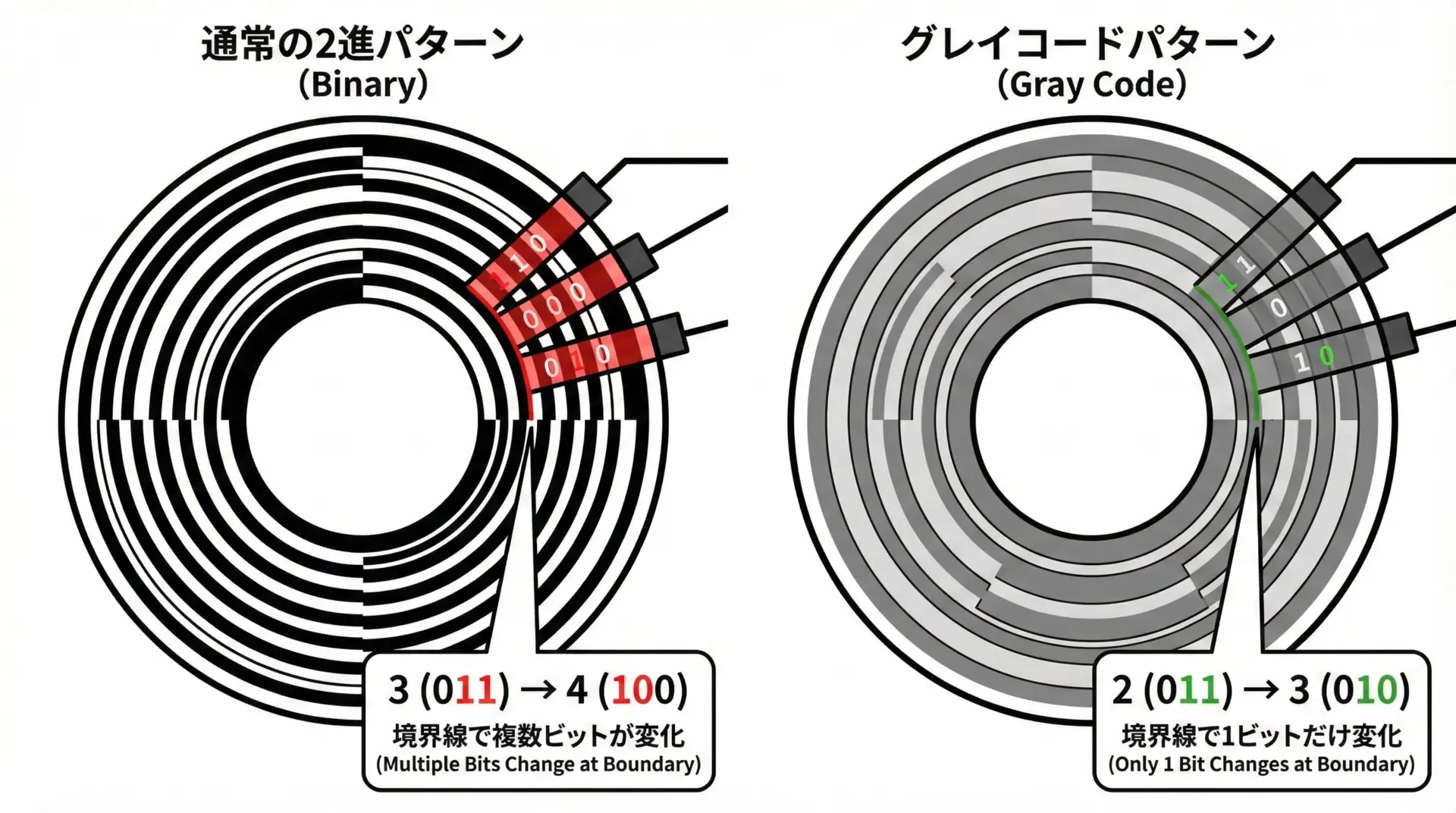
グレイコードの代表的な応用が回転エンコーダです。

回転エンコーダとは、モータやシャフトの回転角度を検出するためのセンサで、多くの場合、円盤のパターンを光学的に読み取って位置をビット列として出力します。

通常の2進数パターンを使うと、ある角度の境界付近で複数ビットが同時に変化します。

その瞬間に読み取りタイミングがずれると、

本当は「0111」なのに「0000」と誤読
連続した物理位置なのに、大きく飛んだ数値として認識

といった深刻な誤差が生じることがあります。

そこで、エンコーダではパターンをグレイコードにしておくことで、ある角度から次の角度に移るとき、ビットは必ず1つしか変わらないようにデザインできます。

すると、仮に読み取りがずれても、誤差は隣接位置(1カウント分)以内に抑えられるため、安定した角度検出が可能になります。

アドレス線・状態遷移のグリッチ(一時的誤り)削減

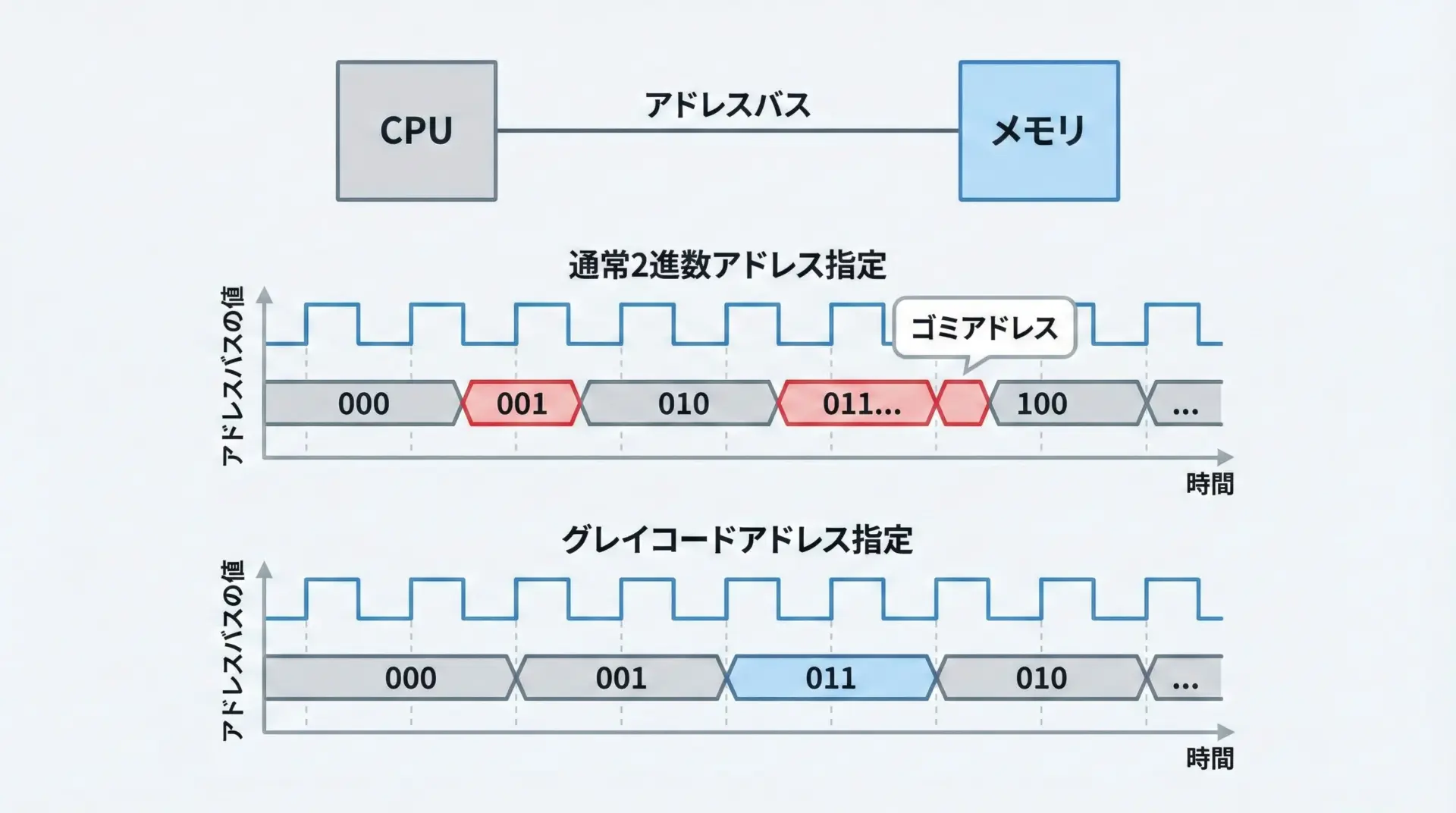
メモリや外部デバイスにアクセスする際に使われるアドレス線でも、グレイコードが使われることがあります。

理由は、アドレスが変化するときに発生しうるグリッチ(一時的な誤ったビットパターン)を軽減したいからです。

通常の2進カウンタでアドレスを順に増やしていくと、例えば0111から1000へのように、複数ビットが同時に変化する場面があります。

この瞬間に回路内で時間差が生じると、一時的に0000や1111など全く別のアドレスが見えてしまう可能性があります。

このような問題を避けるために、内部のカウンタはグレイコードで動かし、必要なタイミングだけ2進数に変換するといった設計が採用されることがあります。

エラー検出や符号設計での活用

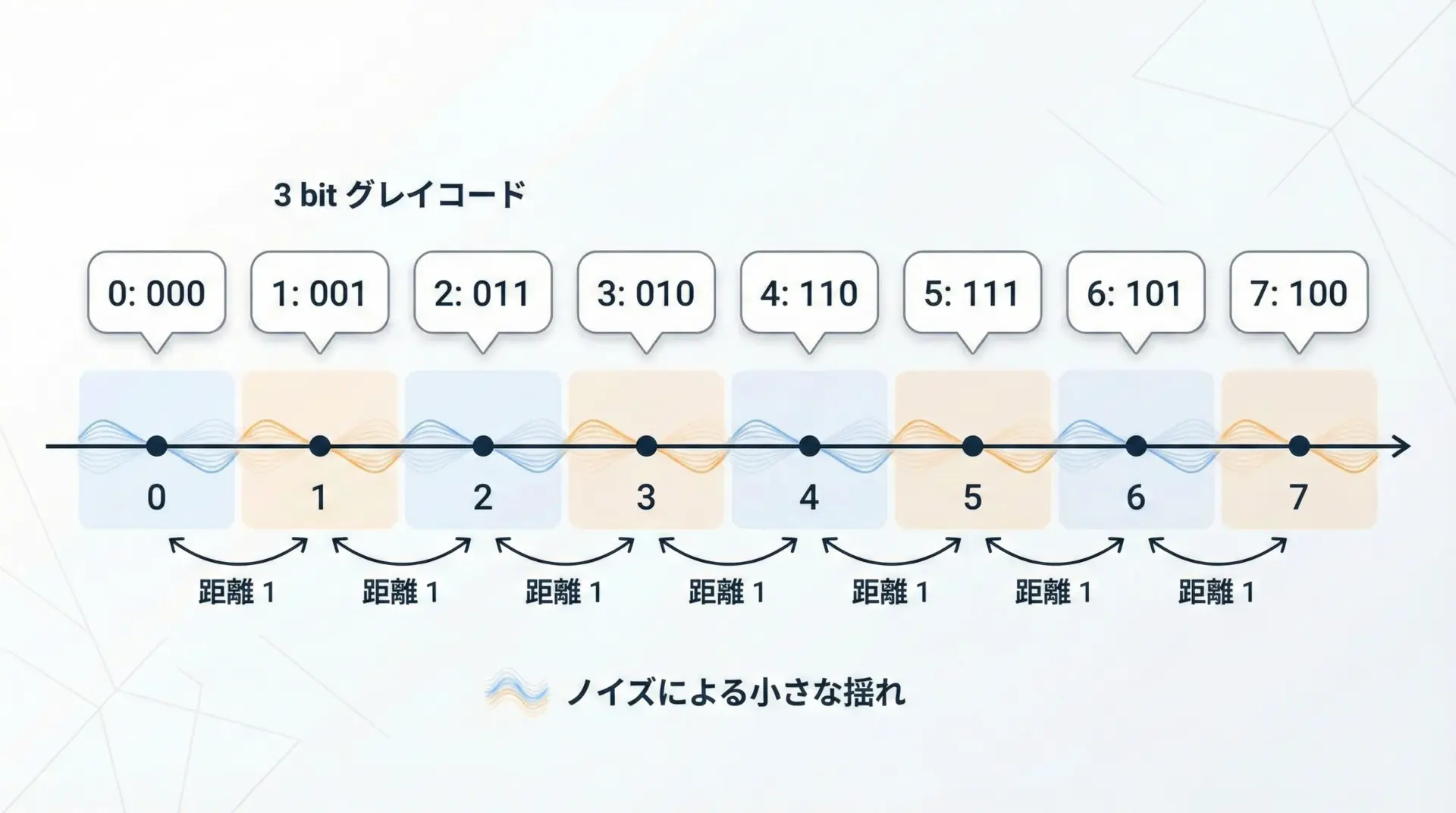
グレイコードは、隣接するコード同士のハミング距離(異なるビット数)が1という性質を持っています。

この性質を利用して、

近い値同士で混同が起きやすい状況で、誤りを局所化する
状態遷移が必ず1ビットずつ変化するような符号設計を行う

といった用途があります。

完全なエラー訂正符号とは異なりますが、物理的な揺らぎやノイズが避けられない環境での「実用的な安全策」として使われるケースが多いです。

グレイコードを直感的に理解するコツ

「1歩ずつしか動かないカウンタ」として捉える

多くの方にとって、グレイコードは初めて見ると少し不自然な並びに感じられます。

しかし、「1歩ずつしか動かないカウンタ」だと考えると直感的に理解しやすくなります。

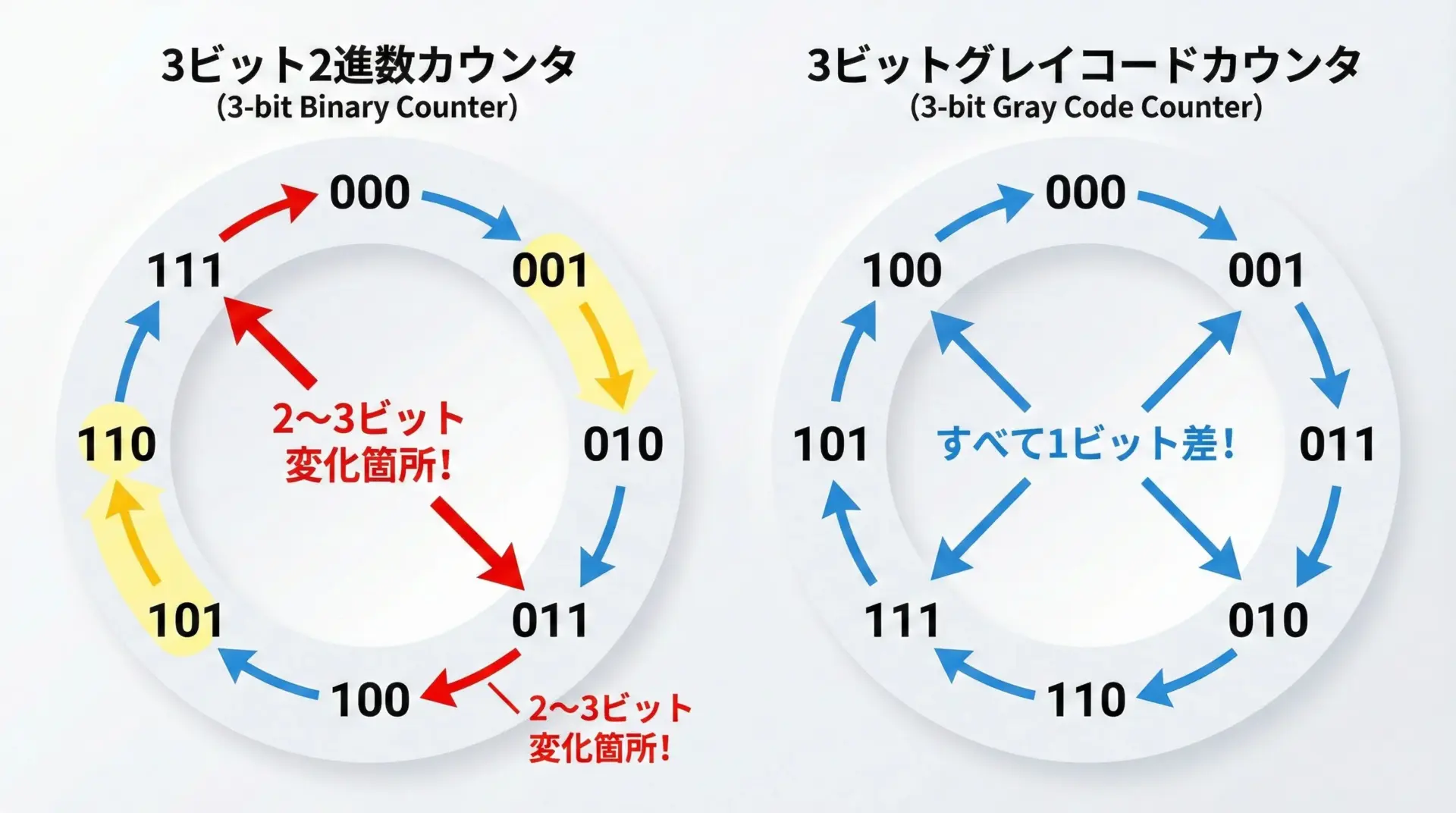
通常の2進カウンタ: 値によっては「大ジャンプ」が起きる(複数ビットが変化)
グレイコードカウンタ: いつでも「隣のマス」にしか移動しない(1ビットだけ変化)

この差が、そのまま誤読時の安全性や、状態の連続性の保証につながります。

「計算用」ではなく「状態表現用」という意識

グレイコードは、加算や乗算のような演算を直接行うための表現ではありません。

むしろ、

物理的な位置
時間的な順番
状態遷移

といった「順序」に意味がある情報を安全に表現するために使う、と考えると理解しやすいです。

計算が必要なときは、いったん通常の2進数に戻してから演算し、また必要に応じてグレイコードに変換する、という使い方をします。

まとめ

グレイコードは、連続する値が必ず1ビットだけ異なるように並んだ2進数表現であり、物理的な信号のタイミングずれやノイズによる誤りを小さく抑えるために広く利用されています。

2進数との相互変換は、XORとシフトだけのシンプルなビット演算で実現でき、組み込みシステムでも扱いやすい形式です。

回転エンコーダやアドレス線、状態遷移の設計など、実世界とデジタルの橋渡しをする場面で特に威力を発揮します。

グレイコードの考え方を押さえておくことで、信頼性の高いデジタルシステム設計に一歩近づくことができます。