「コンピュータの計算は正確で間違えない」と思われがちですが、実際にはぴったり期待どおりの値にならないことが少なくありません。
プログラムで金額を扱ったら端数が合わない、グラフが少しずれて描画される、といった現象の多くは数値誤差が原因です。
本記事では、電卓とコンピュータの違いから始めて、浮動小数点数のしくみ、誤差が生まれるパターン、そして実際のプログラミングでの付き合い方までを、できるだけやさしく整理していきます。
数値誤差とは?コンピュータ計算の「ズレ」の正体
数値誤差とは何か
数値誤差とは、理論的に「正しいはずの値」と、コンピュータが扱う「計算結果の値」とのズレのことです。
紙と鉛筆で数学的に計算すると、式が決まれば答えも1つに決まります。
しかしコンピュータの世界では、同じ式を計算しても、メモリに保存できる桁数や表現方法の制限によって、どうしてもわずかな誤差が入り込みます。
ここで重要なのは、これは「コンピュータが計算を間違えた」というより「最初から有限の桁しか使えないしくみになっている」という点です。
有限の桁数に収めるために、どこかで丸めたり切り捨てたりせざるを得ないため、その影響が少しずつ結果に表れてきます。
電卓とコンピュータの計算は何が違うのか
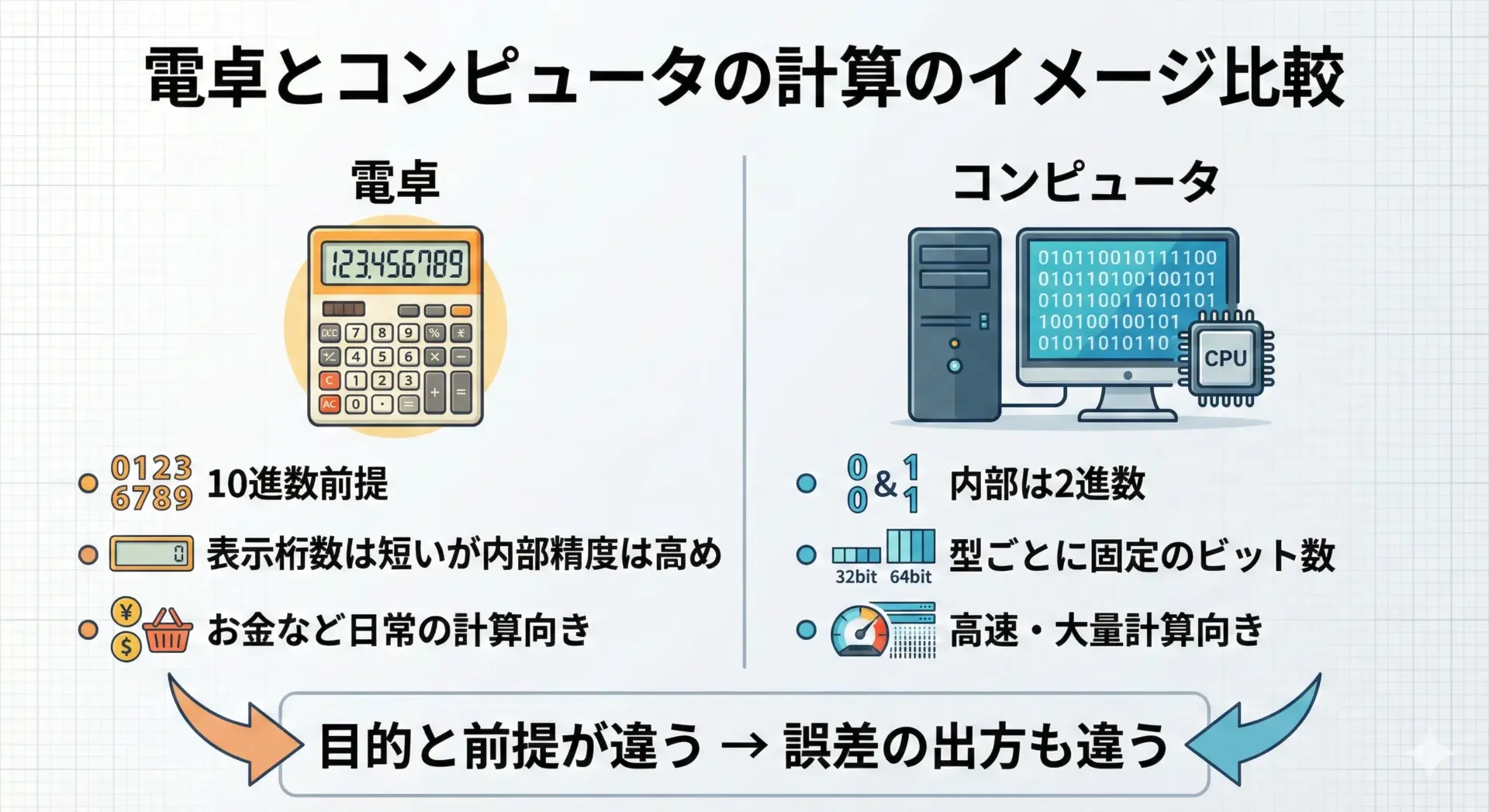
電卓もコンピュータも、どちらも中身は電子回路ですが、目的と前提がかなり異なります。
家庭用の電卓は、多くの場合10進数での「見た目どおりの結果」を重視しており、内部で高めの精度を使って計算し、最後に表示桁数へきれいに丸めてくれます。
小数を多く使う家計簿や売上計算など、人間が10進数で扱う場面に最適化されています。
一方プログラミングで使うコンピュータは2進数(0と1)で高速に大量の計算をすることが主目的です。
数値を表すためのビット数があらかじめ決まっており、その枠からはみ出す情報は切り捨てるしかありません。
また、内部表現は2進数用に最適化されているため、10進数の「きれいな小数」との相性が良くありません。
このため、同じ「0.1」という表示でも、電卓とコンピュータでは内部の持ち方がそもそも違うことが多く、その違いが数値誤差として表面化します。
数値誤差が問題になる具体例
数値誤差は、誤差自体が小さくても、状況によっては大きな問題を引き起こします。
いくつか典型的な例を見てみます。
1つ目は金額計算です。
0.1円、0.01円といった細かい単位で大量のトランザクションを扱うと、1回ごとの誤差はごく小さくても、何万回分も積み重なると数円〜数十円の差になることがあります。
金融や課金システムでは、この差は無視できません。
2つ目はシミュレーションや数値解析です。
物理シミュレーション、機械学習の重み更新、統計解析などでは、同じ式を何千回、何万回と繰り返し計算することが一般的です。
このときわずかな数値誤差が毎回加算・乗算され、長い時間をかけて大きく膨らむ場合があります。
3つ目は判定ロジックです。
例えばif (x == 0.3)のように、浮動小数点数同士をぴったり比較していると、「理論上は等しいはずなのに、内部表現の差で不一致になる」といったバグを生むことがあります。
コンピュータはどうやって数を表現しているか
整数型と浮動小数点型の違い
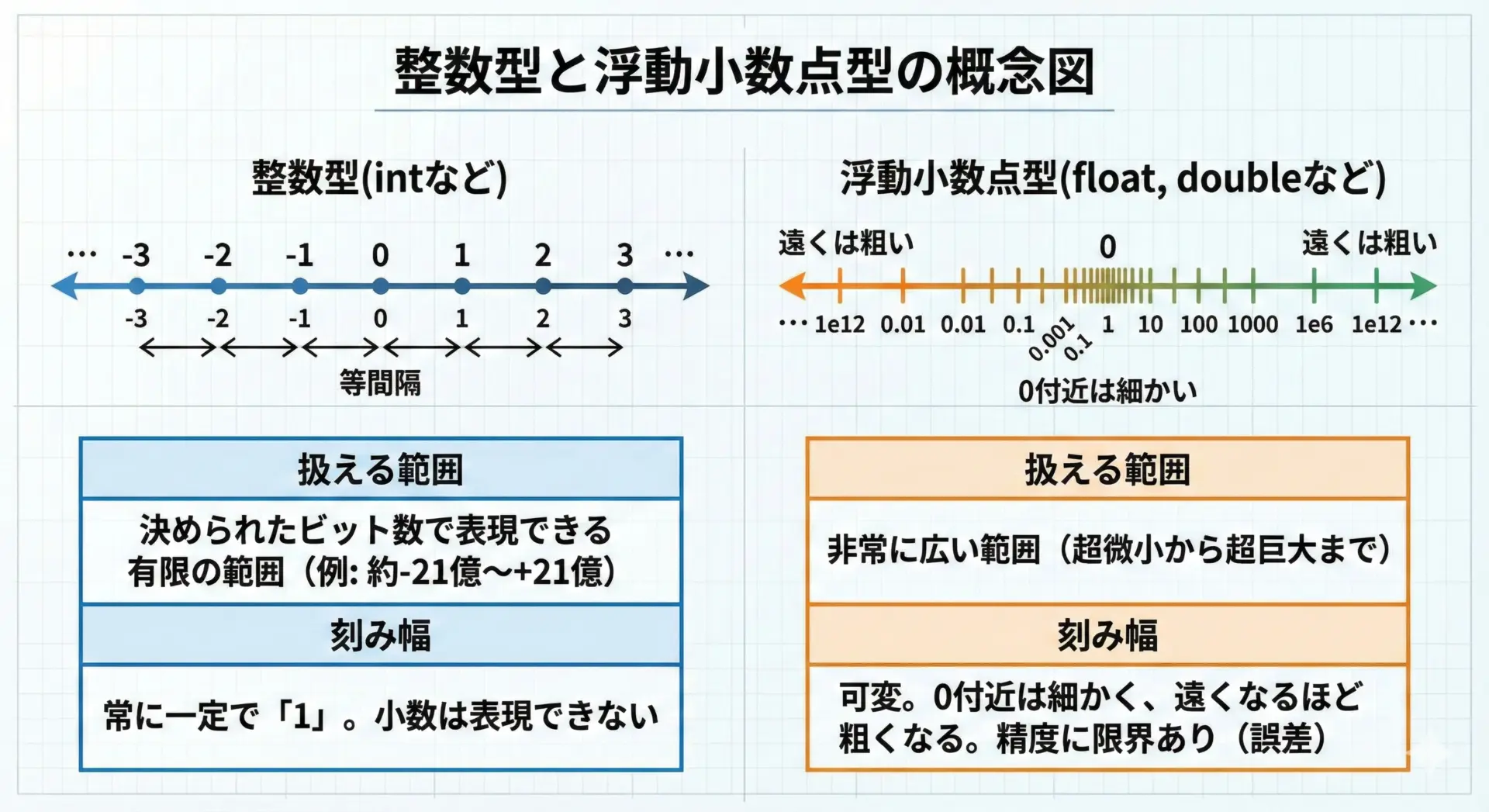
コンピュータで数値を扱うとき、基本となるのが整数型と浮動小数点型です。
整数型(int, longなど)は、小数点を持たない整数をそのまま2進数で表現します。
例えば1なら0001、2なら0010といった具合です。
表現できる範囲はビット数で決まり、32ビットの符号付き整数ならおおよそ-2,147,483,648から2,147,483,647までです。
整数は表現できる値に誤差がなく、加減乗除も原則としてぴったり計算できるという特徴があります。
一方の浮動小数点型(float, doubleなど)は、非常に大きな数から非常に小さな数まで、広い範囲を小数付きで表現できるよう設計されています。
ただしその代わりに、すべての実数を正確に表現できるわけではなく、近い値で近似することになります。
数値誤差の多くはこの浮動小数点表現に由来します。
2進数と10進数のズレが生む誤差のしくみ
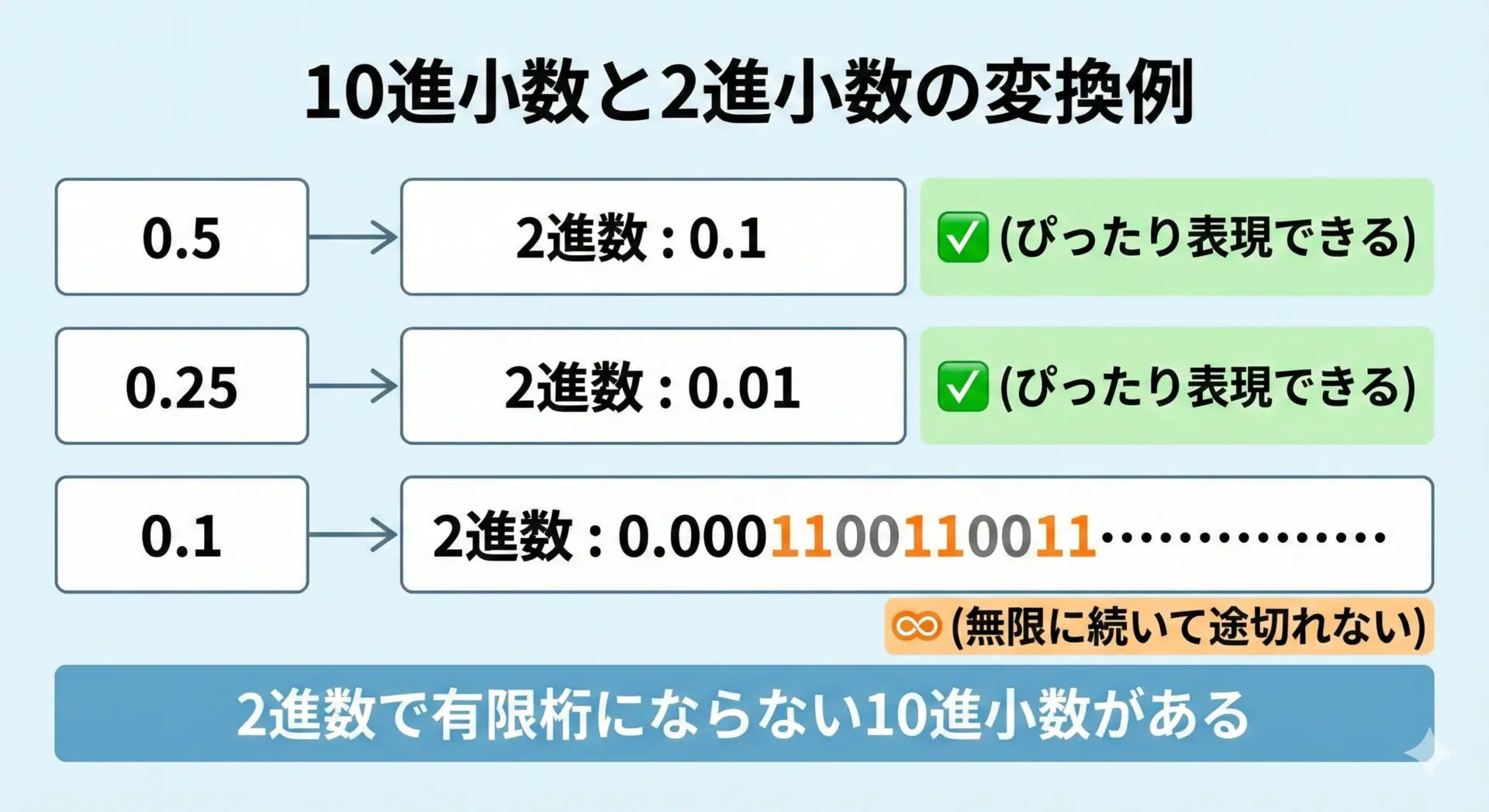
10進数の世界では、1/2 = 0.5, 1/4 = 0.25のように、きれいな小数で表現できる分数がたくさんあります。
しかし、これをそのまま2進数に直そうとすると事情が変わります。
2進数では、分母が2の累乗の分数(1/2, 1/4, 1/8, …)だけが有限桁の小数として表現できます。
例えば0.5は0.1(2進)、0.25は0.01(2進)と、すっきり書けます。
ところが0.1(10進)は、2進数では0.0001100110011…と無限に続く小数になってしまいます。
これは、10進数で1/3 = 0.3333…と永遠に続いてしまうのと同じ現象です。
2進数にとって「苦手」な小数が存在するわけです。
コンピュータは有限のビット数しか持てないため、この無限小数0.000110011…をどこかで打ち切る必要があります。
この「どこかで打ち切る」ところで、すでに誤差が発生していることになります。
浮動小数点数(float,double)の内部表現
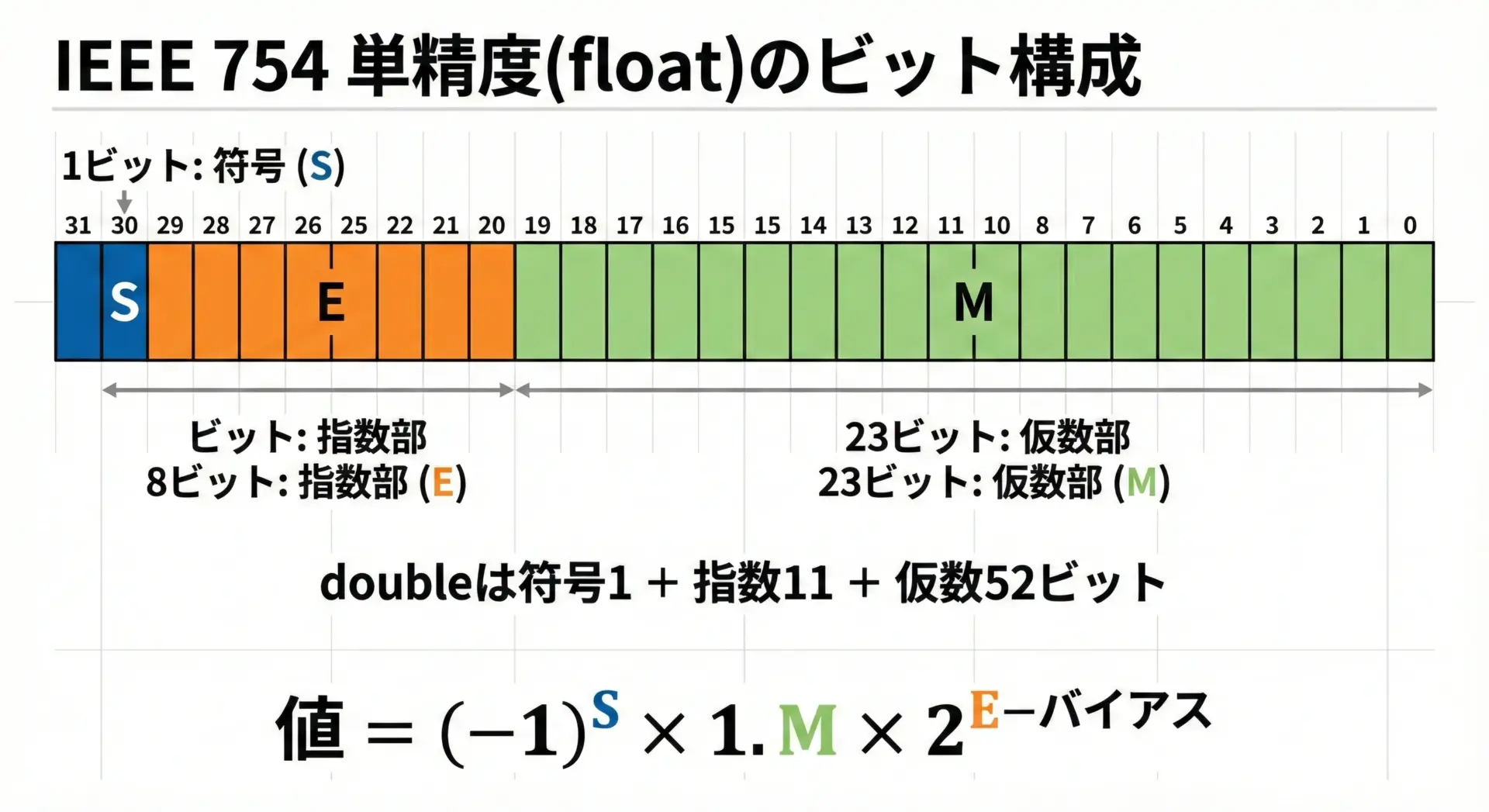
多くのプログラミング言語では、浮動小数点数はIEEE 754という国際規格に沿って表現されています。
代表的なものは次の2つです。
- 単精度浮動小数点数(float): 32ビット
- 倍精度浮動小数点数(double): 64ビット
内部的には、どちらもおおむね次の3つの部分で構成されています。
- 符号ビット(S): プラスかマイナスか
- 指数部(E): 2の何乗か(スケールの大きさ)
- 仮数部(M): 有効桁に相当する部分
値はイメージとして値 = (-1)^S × 1.M × 2^(E - バイアス)のように解釈されます。
ここで1.Mは「1.xxx…」という形の2進小数です。
この表現方法のおかげで、とても大きな数(例: 10^38付近)から、とても小さな数(例: 10^-38付近)までを限られたビット数で扱うことができます。
その代わりに、「どの数も同じ精度で表現できるわけではなく、有効桁数が決まってしまう」という制約が生まれます。
表現できる桁数と丸め込み(丸め誤差)の関係
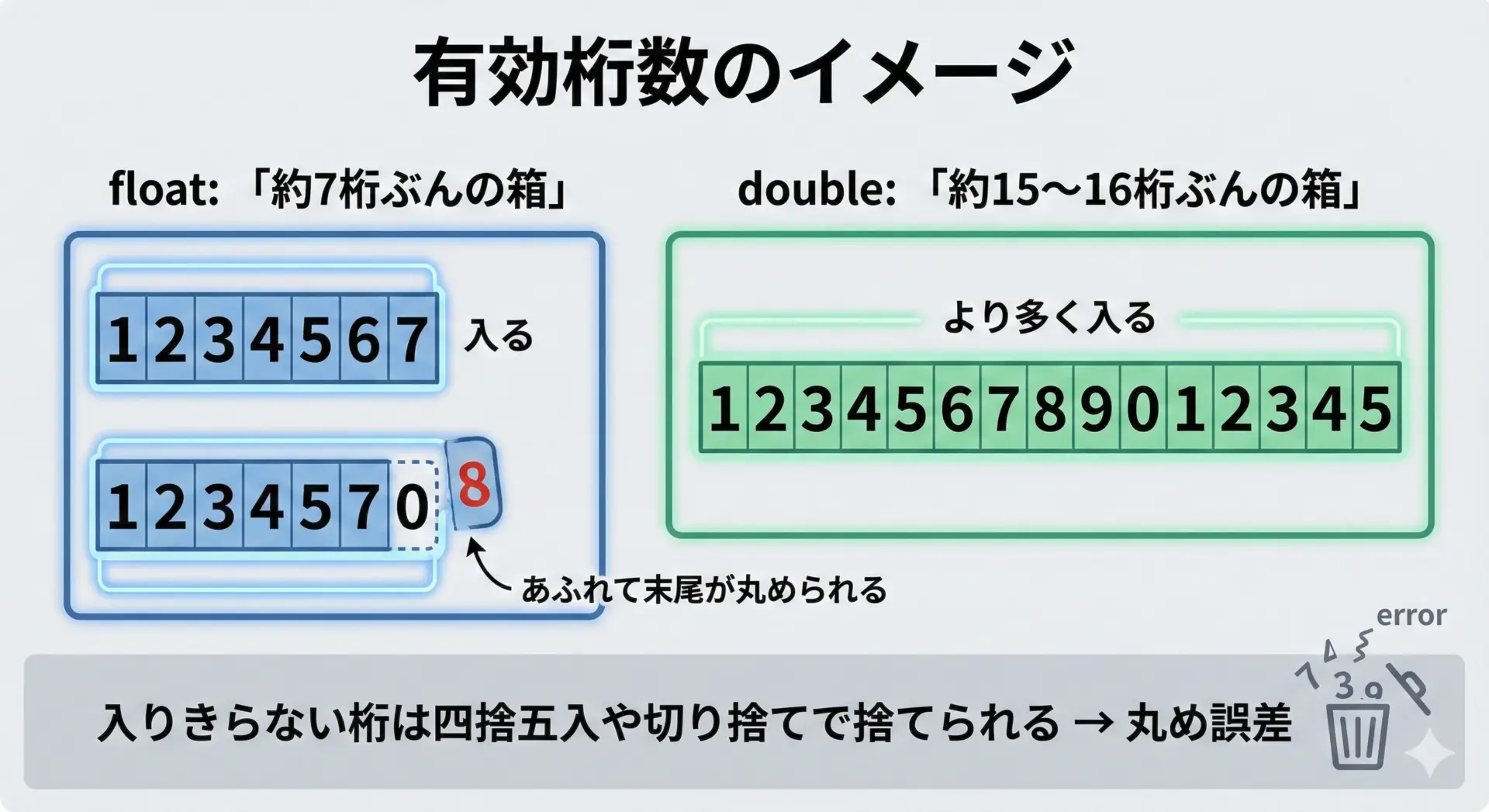
浮動小数点数には、「有効数字として保証できる桁数」が有限という性質があります。
おおまかには次のように覚えておくと便利です。
- float: 約7桁程度の有効数字
- double: 約15〜16桁程度の有効数字
つまり、doubleであっても、それ以上の桁を厳密に保持することはできません。
入りきらない桁は、何らかのルールで丸めたり切り捨てたりされることになります。
このときに生まれるのが丸め誤差です。
例えば、本来の値が1.234567890123456であっても、doubleでは1.23456789012346のように、下のほうの桁が少しだけズレることがあります。
このズレ自体は非常に小さいのですが、後述するように、計算方法次第では無視できない大きさに育ってしまう場合があります。
数値誤差が起きる主な原因
丸め誤差
丸め誤差は、表現できる桁数に収まらない部分を切り捨てたり丸めたりすることで生じる誤差です。
先ほど触れた「0.1を2進数で表せない問題」は、まさにこの典型例です。

プログラムでfloat x = 0.1f;と書いた時点で、実際には0.10000000149011612…のような「0.1に非常に近いがぴったりではない値」がメモリに入っています。
この差が、後の計算でじわじわ効いてきます。
桁落ち
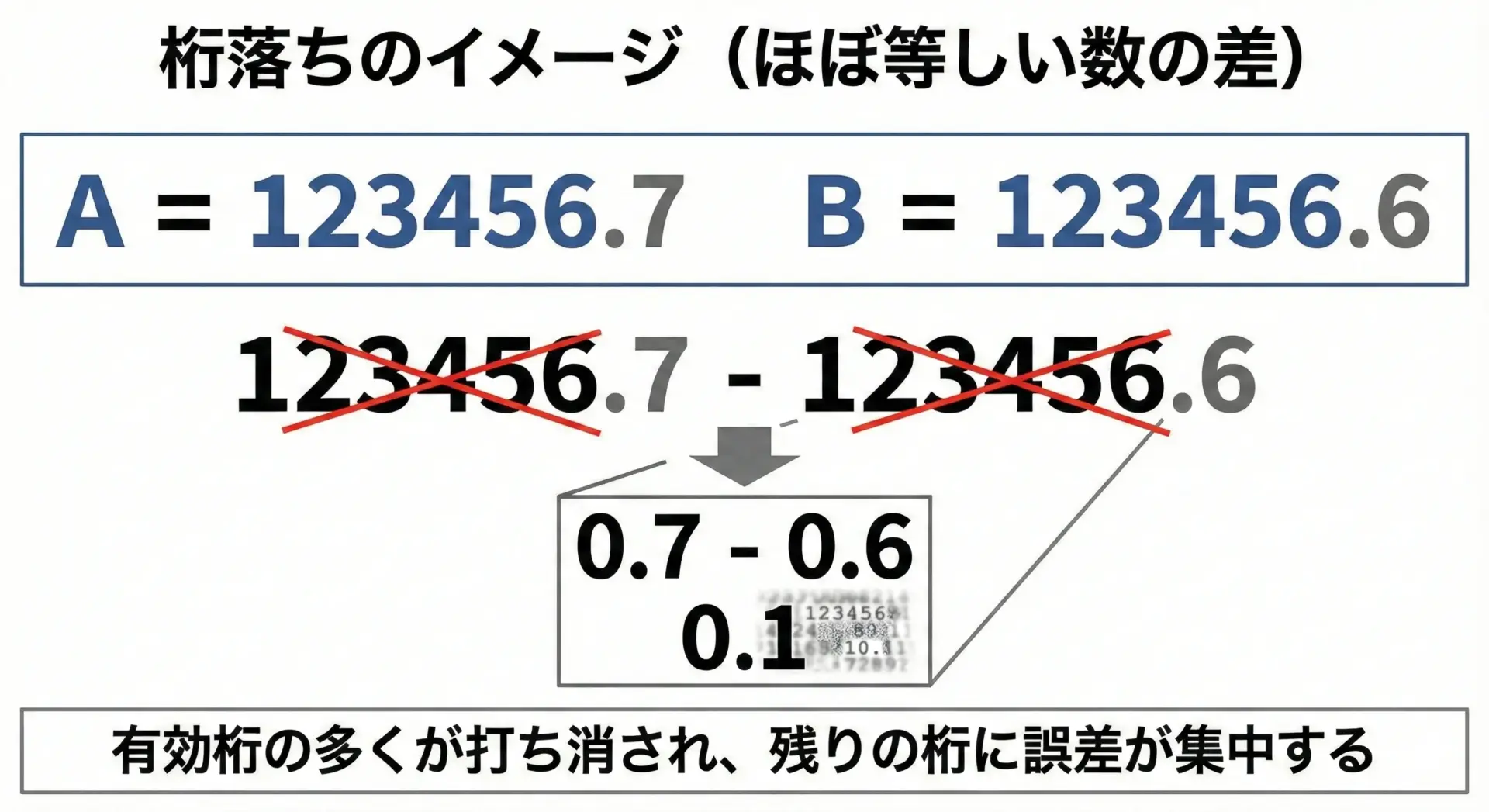
桁落ちは、ほとんど同じ大きさの2つの数を引き算するときに、上位の有効桁が打ち消されてしまい、下位の桁だけが残る現象です。
例えば、有効数字7桁程度しか信頼できないfloatで、
- A = 123456.7
- B = 123456.6
といった値を持っていたとします。
このときAとB自体は丸め誤差を含みつつも7桁分はそこそこ正確ですが、A - Bを計算すると、本来の答えは0.1です。
しかし、実際は
- 上位の
123456.部分が差し引きでキャンセルされ、 - 残ったごくわずかな差分
0.1だけに、もともとの丸め誤差が集中
してしまいます。
その結果、相対的には非常に大きな誤差になってしまうことがあります。
情報落ち
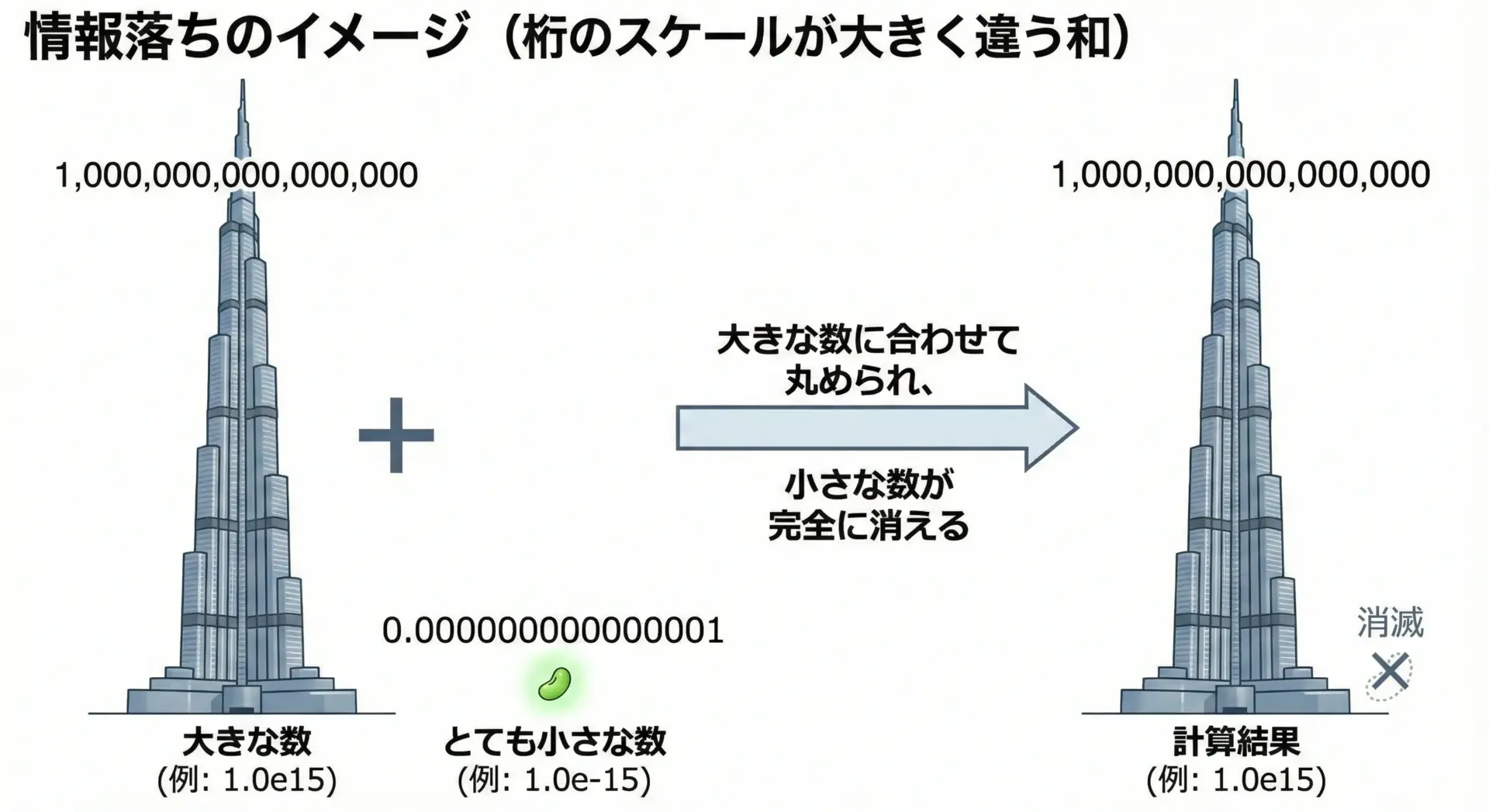
情報落ちは、非常に大きな数と、非常に小さな数を足し合わせるときに、小さいほうの値が有効桁からはみ出してしまい、完全に無視される現象です。
例えばdoubleで、
- A = 1.0e16
- B = 1.0
としたときにA + Bを計算すると、論理的には1.0000000000000001e16のような値になるはずですが、実際には有効桁数の制限で、Bの「1」が有効桁に乗り切らず、結果がAと全く同じ値になってしまうことがあります。
つまり、「1を足した」という情報がどこかで落ちてしまうのです。
繰り返し計算で誤差が累積する理由
丸め誤差や桁落ち、情報落ちといった現象は、1回の計算だけなら「ほとんど気づかない」程度で済むことが多いです。
しかし、同じような計算を何千回、何万回と繰り返すと、その小さな誤差が足し合わされていくことになります。
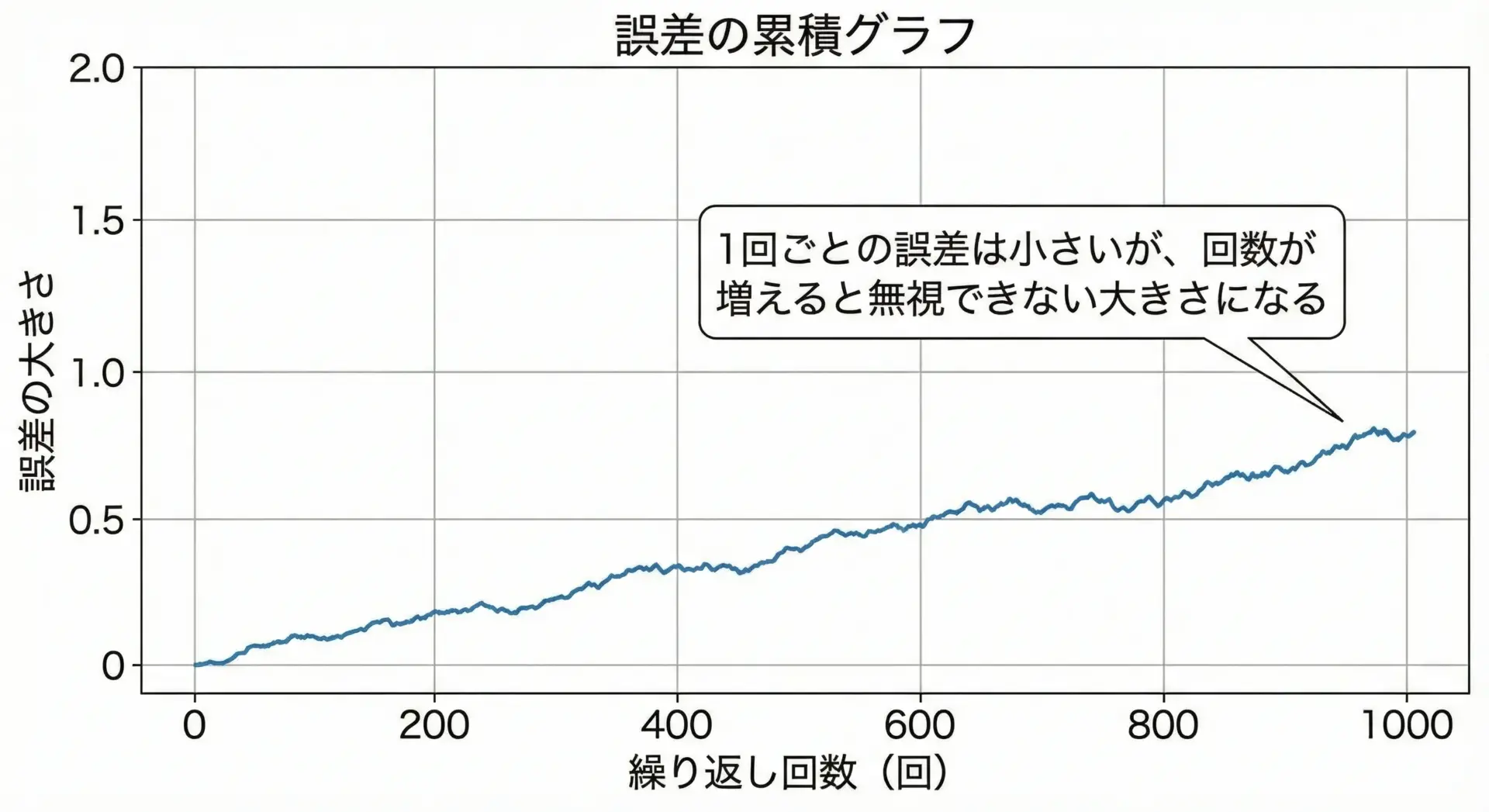
例えば、
x = 0.0
for i in 1..1000000:
x = x + 0.1のようなコードを考えてみます。
理論上はx = 100000.0になるはずですが、実際には99999.99…や100000.00000001のように、わずかにずれた値になることがほとんどです。
毎回の加算で「0.1に近いが完全ではない値」を足しているため、その差分が100万回も積み上がるからです。
オーバーフロー・アンダーフローとは何か
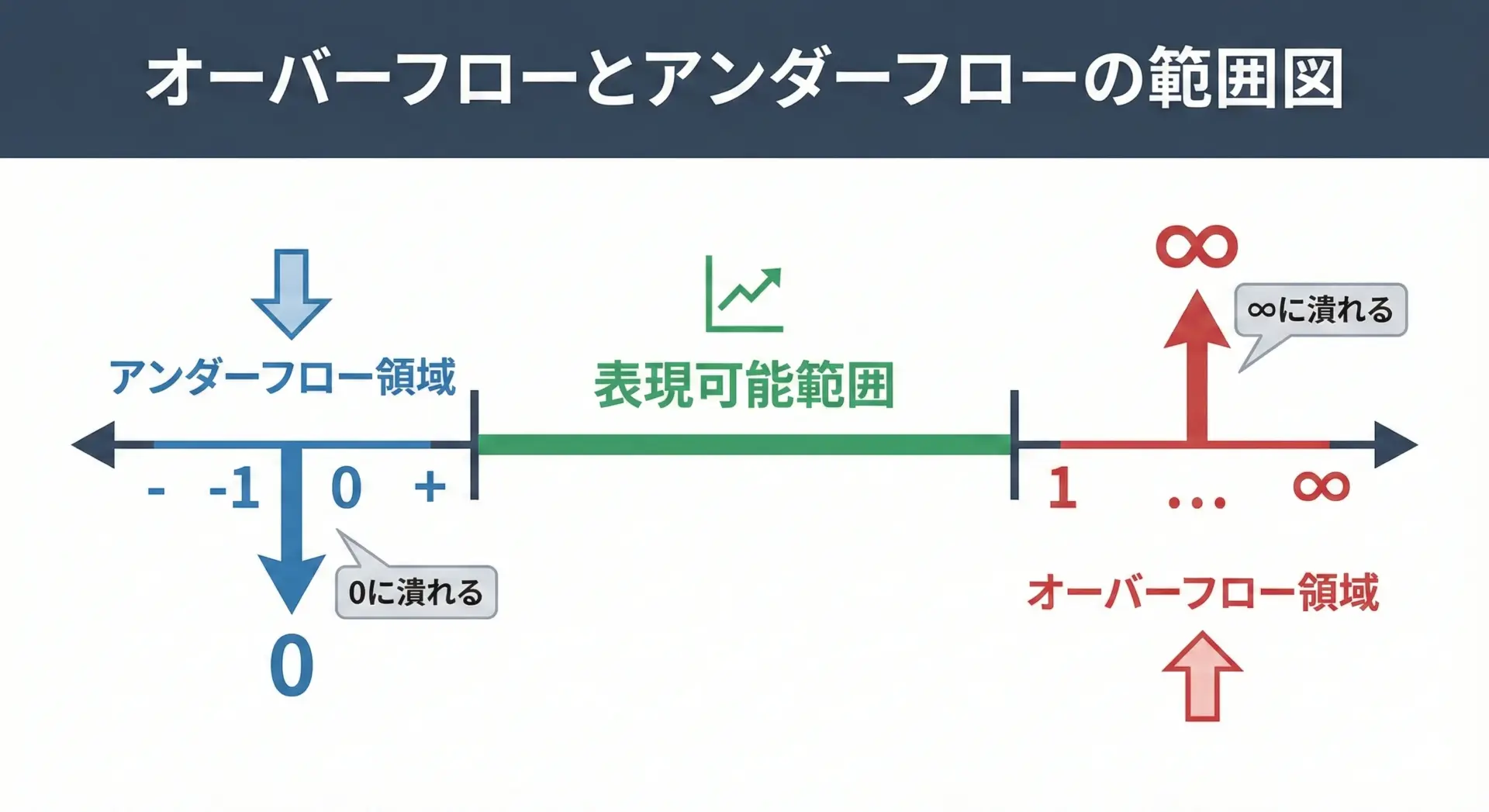
数値誤差とセットで理解しておきたいのがオーバーフローとアンダーフローです。
- オーバーフロー:
型が表現できる最大値を超える大きな数を扱おうとしたときに発生します。IEEE 754の浮動小数点では、多くの場合Infinity(無限大)や-Infinityとして表現されます。 - アンダーフロー:
型が表現できる最小の正の値よりも、さらに絶対値が小さい数を扱おうとしたときに起きます。この場合は0になってしまったり、0にかなり近いサブノーマル数と呼ばれる特別な表現になったりします。
オーバーフローやアンダーフローが起きると、それ以降の計算結果が極端におかしくなることが多いため、数値計算では特に注意が必要です。
プログラミングで数値誤差と上手につき合うコツ
「0.1+0.2==0.3」が危ない理由と比較のコツ
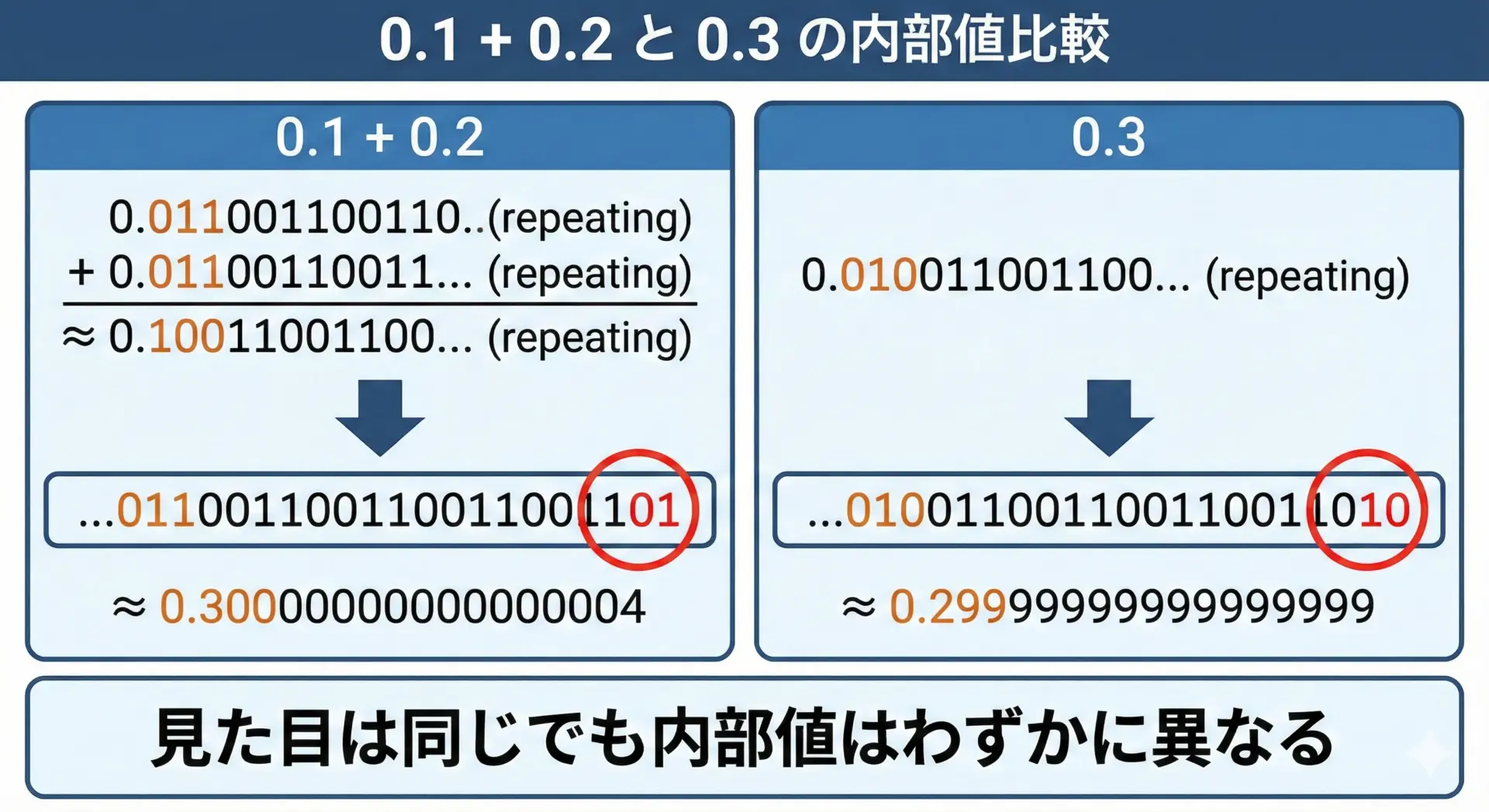
プログラミングを学び始めた人がよく引っかかるのが、0.1 + 0.2 == 0.3のような比較です。
多くの言語でこの式を評価すると、falseになります。
これは、先ほど説明したように0.1も0.2も0.3も、いずれも2進数ではぴったり表現できないためです。
それぞれが「本来の値に非常に近い近似値」としてメモリに保存されており、
0.1 + 0.2の結果の近似値0.3として直接保存した近似値
が、別々の丸め過程を経ているため、内部的にわずかに異なる値になります。
その差は通常、10進数で小数点以下16桁目など、極めて小さなものですが、==演算子は完全一致を要求するため、不一致となってしまうわけです。
この問題を避けるためには、浮動小数点数の等値比較では「許容誤差(イプシロン)」を使うのが定番です。
例えば疑似コードで書くと、次のようなイメージです。
epsilon = 1e-9
if abs((0.1 + 0.2) - 0.3) < epsilon:
// ほぼ等しいとみなすこのように、「差の絶対値が十分小さければ同じと見なす」という考え方に切り替えることで、ほとんどの実用的な場面では問題を回避できます。
浮動小数点を避けたい場面での対処法
金額や個数など、小数点以下の桁数が決まっていて、かつ誤差が許されない場面では、そもそも浮動小数点を使わないほうが安全です。
代表的な対処法として、次のようなものがあります。
- 整数で扱う
金額なら「円」ではなく「銭(1/100円)」や「ミリ単位」に変換して、整数型で計算します。例えば1.23円なら123銭としてintに入れる、といった具合です。整数演算であれば、表現できる範囲内では誤差なく計算できるため、金額計算に向いています。
- 10進小数専用の型を使う
言語やライブラリによっては、decimal型やBigDecimalのように、10進数に最適化された高精度小数型が用意されています。内部的に10進数の桁をそのまま持つことで、「0.1」などの小数を正確に表現できます。その代わり、演算速度やメモリ消費は浮動小数点より重くなります。
- 任意精度演算ライブラリを使う
数値解析や暗号など、非常に高い精度が必要な計算では、任意桁精度のライブラリ(任意精度整数、任意精度小数)を使うことがあります。計算コストは増えますが、必要なだけ桁数を確保できます。
計算順序を工夫して誤差を減らすテクニック
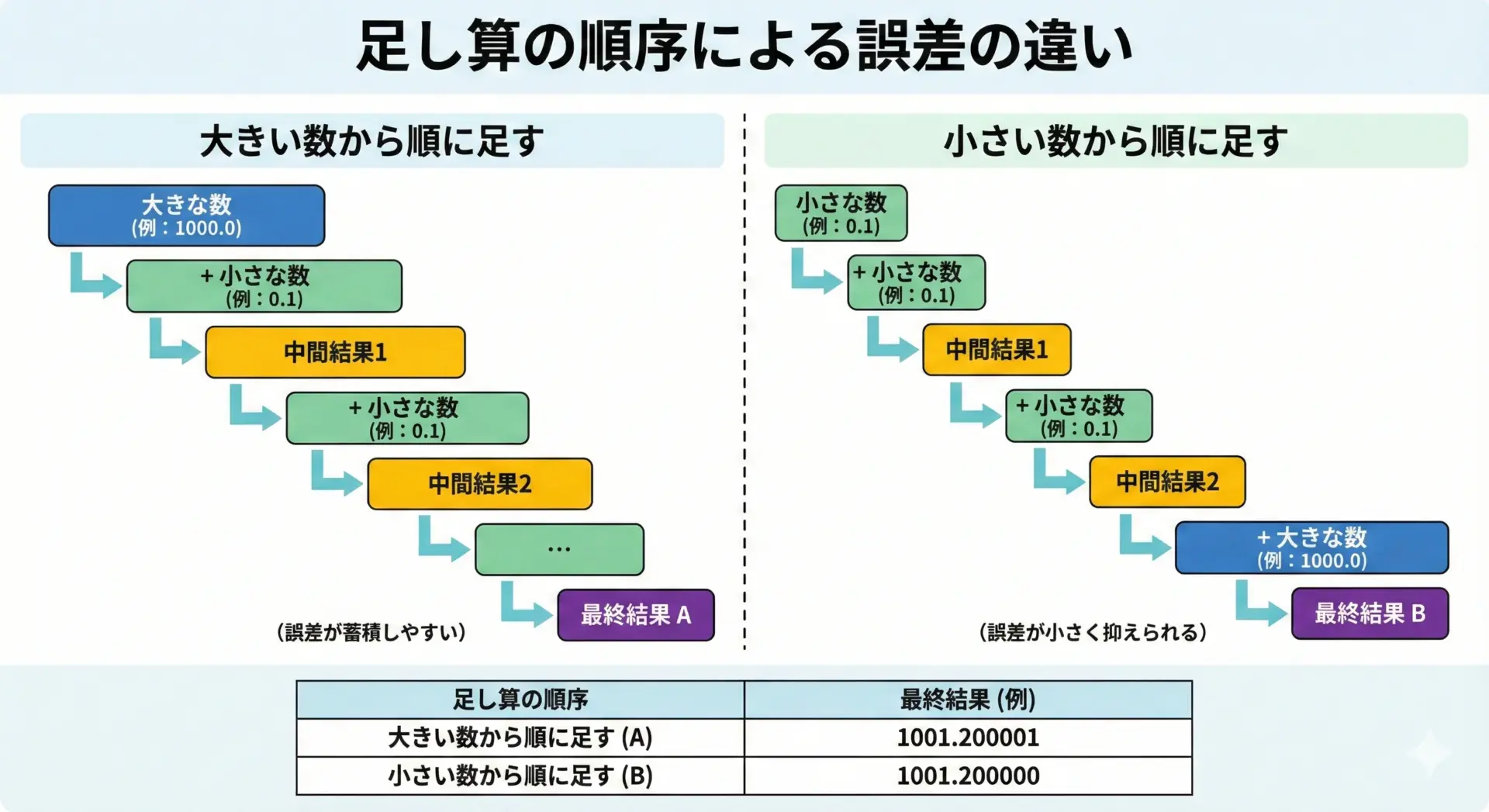
浮動小数点の世界では、同じ数列の和であっても、足し合わせる順番を変えるだけで結果が変わることがあります。
これは、途中結果の大きさに応じて丸め誤差や情報落ちの影響が変化するためです。
例えば、非常に大きな数と非常に小さな数が混ざったリスト[1e16, 1.0, 1.0, 1.0, …]を合計するとき、
- 大きな数から順に足していくと、小さな1.0が情報落ちしてしまう
- 小さな数同士を先に合計し、最後に大きな数を足すと、1.0の寄与分をある程度保てる
といった違いが生まれます。
具体的なテクニックとしては、次のようなものがあります。
- 大きさの近い数同士を先にまとめて計算する
- 配列の値を昇順または降順にソートしてから加算する
- Kahan和アルゴリズムのような、誤差を補償する加算アルゴリズムを利用する
Kahan和のイメージは、これまでの丸め誤差を「補償値」として別に持っておき、次の加算時にその分を調整するというものです。
実装は少し複雑になりますが、大量の浮動小数点を足し合わせる場合には有効です。
初心者が覚えておきたい数値計算の注意ポイント
最後に、プログラミング初心者の方がまず押さえておきたい注意点を、実践的な観点からまとめます。
- 浮動小数点の
==比較は極力避ける
等しいかどうかを判定したいときは、abs(a - b) < epsilonのような「許容誤差つき比較」を検討します。 - 金額や個数など「誤差が困るもの」は、まず整数で表現できないか考える
どうしても小数が必要なら、decimal系の型の有無も調べてみてください。 - ループで少しずつ足し続ける計算は、誤差が累積するものだと意識する
回数が多い場合は、計算順序を変えたり、途中でまとめて合計するなど、誤差の増え方を抑える工夫を検討します。 - きれいな式変形が、必ずしも数値的に安定とは限らない
数学的に同値な式でも、数値的には桁落ちや情報落ちを起こしやすい形があります。分母が非常に小さくなる式や、ほぼ等しい2つの差分などは特に注意が必要です。 - オーバーフロー・アンダーフローが起き得る範囲を知っておく
使用している言語や環境のfloatやdoubleの最小値・最大値を一度調べておくと、極端な値を扱うときのヒントになります。
まとめ
本記事では、コンピュータの数値計算における数値誤差について、その正体と原因、そして実際のプログラミングでの向き合い方を解説しました。
コンピュータは、有限のビット数で2進数を扱うという制約のもとで動いています。
この制約から、0.1のような「人間にとって自然な10進小数」がぴったり表現できないことが生まれ、さらに有効桁数の限界によって、丸め誤差・桁落ち・情報落ちといった現象が起こります。
そして、それらの小さなズレが繰り返し計算で累積したり、オーバーフロー・アンダーフローによって極端な結果になったりします。
一方で、数値誤差は「バグ」ではなく「前提条件」でもあります。
この前提を理解したうえで、
- 等値比較に許容誤差を使う
- 整数や10進小数型で表現できるものはそうする
- 計算順序やアルゴリズムを工夫して誤差を抑える
といった対策を採れば、多くの問題は十分にコントロールできます。
数値誤差を完全になくすことはできませんが、その性質を知っておけば、「どこまでなら許容できるか」「どこからが危険か」を判断できるようになります。
プログラムが思ったとおりの数字を返してくれないとき、背後には今回紹介したどの要因が潜んでいるのか、ぜひ一度立ち止まって考えてみてください。

