C言語で浮動小数点を扱っていると、計算結果が非常に大きくなりすぎて無限大になったり、0で割るなどしてNaN(Not a Number)が発生したりします。
これらを正しく判定・比較しないと、バグや予期せぬ動作につながります。
本記事では、C言語の無限大とNaNの基本から、標準的な判定方法、例外処理の考え方、実用的なサンプルコードまで、丁寧に解説していきます。
C言語における無限大とNaNとは何か
無限大とNaNの概要
無限大(infinity)とは
無限大(infinity)とは、浮動小数点計算で表現できる最大値を超えてしまった結果として表される「限りなく大きい値」の記号的な表現です。
C言語では、主にIEEE 754という浮動小数点標準に基づいて無限大を表現しています。
代表的な発生例として、次のようなものがあります。
- 非ゼロ値を0.0で割った場合
- 非常に大きな値同士の乗算でオーバーフローした場合
- 指数関数などで演算結果が範囲を超えた場合
浮動小数点には正の無限大と負の無限大があります。
NaN(Not a Number)とは
一方、NaN(Not a Number)は「数として意味を持たない結果」を表す特別な値です。
算術的に定義されない演算、あるいは無効な演算の結果として生成されます。
代表的な発生例は次の通りです。
- 0 / 0.0
- 無限大同士の引き算(∞ − ∞)
- 負の数の平方根(sqrt(-1.0))など
- NaNを含む計算(多くの場合、結果もNaNになります)
NaNは「エラー値」ではなく「伝播する特殊な数値」という点が重要です。
無限大・NaNが必要になる理由
計算を途中で止めず「状態」として伝えるため
もし無限大やNaNという概念がなければ、オーバーフローや不正計算が起こるたびに即座にプログラムを止めるか、あるいは適当な最大値で打ち切らなければなりません。
無限大やNaNを導入することで、「異常な状態」を数値として表現し、後続処理へと伝えることができます。
これにより、後から検査してログを取ったり、特別な処理に分岐させたりすることが可能になります。
数値計算での安全性とデバッグのしやすさ
特に数値シミュレーションや統計分析では、計算の途中で極端な値が出ることは珍しくありません。
無限大やNaNを適切に判定することで、次のような利点があります。
- 異常値にいち早く気づける
- 異常が発生した「位置」を特定しやすくなる
- エラー発生後も、ログ出力や後処理を安全に行える
「想定外の0除算」や「負数の平方根」などを見逃さないためにも、無限大とNaNの扱いを理解することは非常に重要です。
IEEE 754とC言語の関係
IEEE 754とは
IEEE 754は、浮動小数点数の表現と演算ルールを定めた国際標準規格です。
C言語のfloatやdouble型は、ほとんどの環境でこのIEEE 754に従って実装されています。
IEEE 754では、通常の数値だけでなく、無限大やNaN、さらに符号付きゼロ(+0.0と-0.0)なども定義されています。
C言語でIEEE 754が前提になる理由
C言語の標準仕様自体は「必ずIEEE 754であれ」とは言っていませんが、現代の一般的なCPUとコンパイラ環境では、IEEE 754が事実上の前提となっています。
したがって、無限大やNaNの挙動について解説する際も、IEEE 754準拠の実装を仮定して話を進めます。
無限大の生成と判定
無限大を生成する方法
標準ヘッダによる生成(math.h)
最も標準的な方法は、math.hに定義されているINFINITYマクロを使う方法です。
#include <stdio.h>
#include <math.h>
int main(void) {
// math.h で定義されている無限大
float pos_inf_f = INFINITY; // float型の正の無限大
double pos_inf = INFINITY; // doubleへも代入可能
// 負の無限大は符号をつけて生成
double neg_inf = -INFINITY;
printf("pos_inf_f = %f\n", pos_inf_f);
printf("pos_inf = %f\n", pos_inf);
printf("neg_inf = %f\n", neg_inf);
return 0;
}pos_inf_f = inf
pos_inf = inf
neg_inf = -inf多くの実装ではprintfで無限大を出力するとinfやinfinityと表示されます。
計算結果としての無限大
計算の結果として無限大が発生する典型例です。
#include <stdio.h>
#include <math.h>
int main(void) {
double a = 1.0;
double b = 0.0;
// 非ゼロ / 0.0 は正または負の無限大 (実装依存の例外発生の可能性あり)
double c = a / b; // 1.0 / 0.0 → +inf (IEEE 754想定)
double big = 1e308;
double d = big * big; // オーバーフロー → +inf が典型的な挙動
printf("a / b = %f\n", c);
printf("big*big= %f\n", d);
return 0;
}a / b = inf
big*big= inf無限大かどうかを判定する
isinf関数による判定
無限大判定にはmath.hで定義されているisinf関数を使います。
#include <stdio.h>
#include <math.h>
void check_value(double x) {
if (isinf(x)) {
if (x > 0) {
printf("値は正の無限大です\n");
} else {
printf("値は負の無限大です\n");
}
} else {
printf("値は無限大ではありません (x = %f)\n", x);
}
}
int main(void) {
double x1 = INFINITY; // 正の無限大
double x2 = -INFINITY; // 負の無限大
double x3 = 123.45; // 通常の値
check_value(x1);
check_value(x2);
check_value(x3);
return 0;
}値は正の無限大です
値は負の無限大です
値は無限大ではありません (x = 123.450000)isinfは、引数が正または負の無限大であれば非0(真)を返し、それ以外なら0(偽)を返します。
isfiniteで「有限かどうか」を判定
逆に、isfinite関数を使うと「無限大でもNaNでもない通常の有限値かどうか」をまとめて判定できます。
#include <stdio.h>
#include <math.h>
void classify(double x) {
if (isnan(x)) {
printf("NaN です\n");
} else if (isinf(x)) {
printf("無限大です\n");
} else if (isfinite(x)) {
printf("有限値です (x = %f)\n", x);
} else {
printf("その他の値です\n");
}
}
int main(void) {
double a = 1.0 / 0.0; // +inf (想定)
double b = 0.0 / 0.0; // NaN (想定)
double c = 123.456; // 有限値
classify(a);
classify(b);
classify(c);
return 0;
}無限大です
NaN です
有限値です (x = 123.456000)図解で理解する無限大の位置づけ
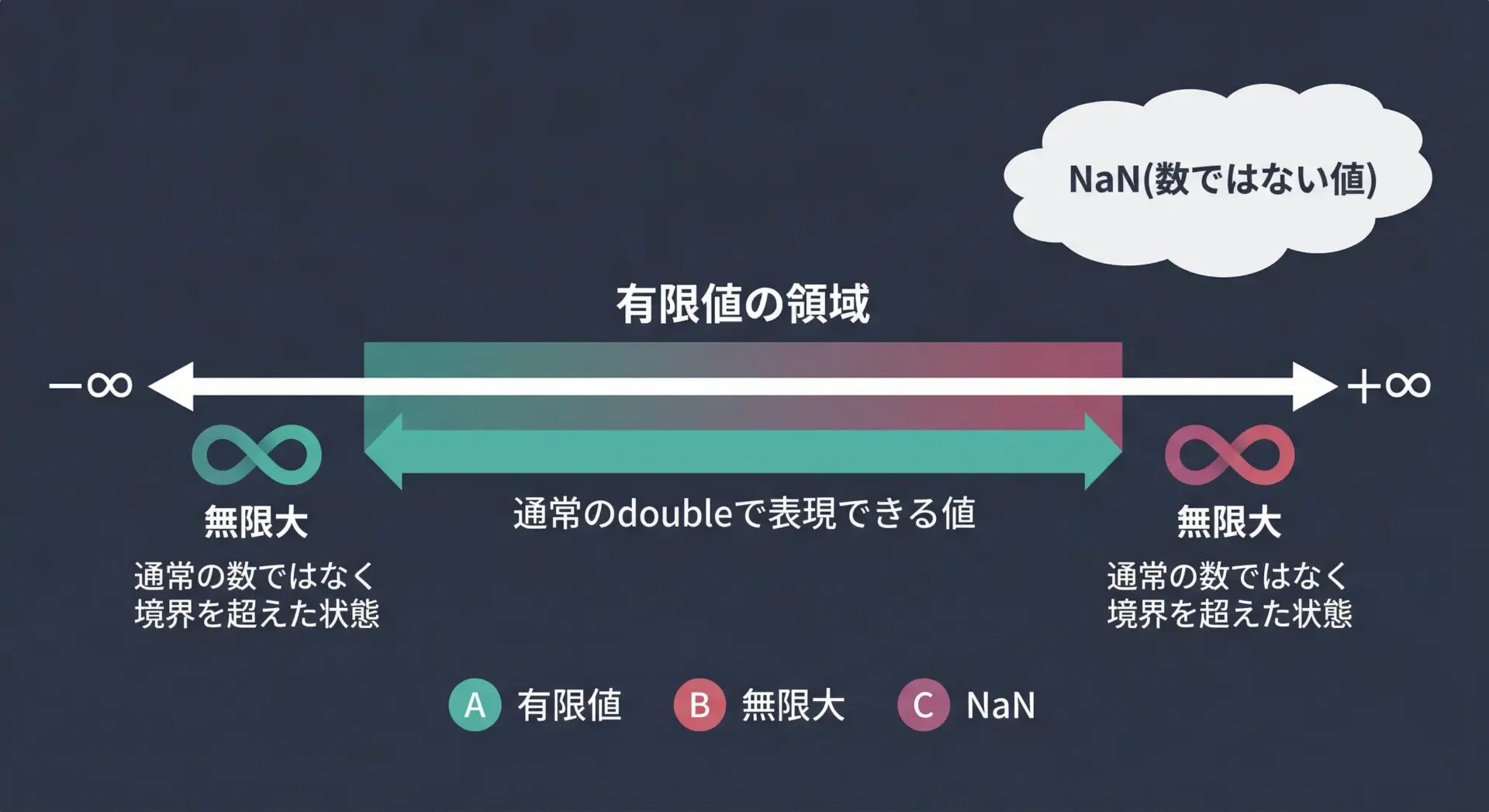
この図では、通常の実数値が実数直線上の有限な区間に収まっているのに対し、無限大はその両端の「果て」を象徴する記号として描かれます。
一方、NaNはそもそも数ではないため、実数直線から少し離れた場所に「別枠」として表現します。
このイメージを持っておくと、無限大は「とても大きな数の延長」にありますが、NaNは「数の世界の外」にあることが直感的に理解しやすくなります。
NaNの生成と判定
NaNを生成する方法
NANマクロを使う
math.hにはNANというマクロが定義されており、浮動小数点のNaN値を直接生成できます。
#include <stdio.h>
#include <math.h>
int main(void) {
float nan_f = NAN; // float型のNaN
double nan_d = NAN; // doubleにも代入できる
printf("nan_f = %f\n", nan_f);
printf("nan_d = %f\n", nan_d);
return 0;
}nan_f = nan
nan_d = nan不正な演算からNaNを発生させる
次のような演算は、多くのIEEE 754実装でNaNを生成します。
#include <stdio.h>
#include <math.h>
int main(void) {
double x1 = 0.0 / 0.0; // 0/0 → NaN (想定)
double x2 = INFINITY - INFINITY; // ∞ - ∞ → NaN (想定)
double x3 = sqrt(-1.0); // 負数の平方根 → NaN (想定)
printf("0.0 / 0.0 = %f\n", x1);
printf("INFINITY - INFINITY = %f\n", x2);
printf("sqrt(-1.0) = %f\n", x3);
return 0;
}0.0 / 0.0 = nan
INFINITY - INFINITY = nan
sqrt(-1.0) = nanNaNがいったん発生すると、多くの演算でその結果もNaNになります。
これを「NaNの伝播」と呼びます。
NaNを判定するisnan
NaNかどうかを判定するにはmath.hのisnan関数を使います。
#include <stdio.h>
#include <math.h>
void check_nan(double x) {
if (isnan(x)) {
printf("値は NaN です\n");
} else {
printf("値は NaN ではありません (x = %f)\n", x);
}
}
int main(void) {
double a = 0.0 / 0.0; // NaN (想定)
double b = 1.0 / 0.0; // +inf (想定)
double c = 42.0; // 有限値
check_nan(a);
check_nan(b);
check_nan(c);
return 0;
}値は NaN です
値は NaN ではありません (x = inf)
値は NaN ではありません (x = 42.000000)isnanは、引数がNaNなら非0(真)を返し、それ以外の値(無限大や有限値を含む)なら0(偽)を返します。
NaNと比較演算の落とし穴
NaNはどの値とも等しくない
NaNの最も重要な性質は「NaNは、自分自身とも等しくない」という点です。
したがって、次のようなコードはNaN判定としては誤りです。
double x = 0.0 / 0.0; // NaN (想定)
// これは NaN 判定としては誤り
if (x == NAN) {
// ここには決して到達しません
}NaN同士を==で比較してもtrueにはなりません。
NaNを判定したい場合はisnanを必ず使います。
自己比較でNaNを検出するトリック
標準的にはisnanを使うべきですが、「値が自分自身と等しくないなら、それはNaNである」という性質を利用することもできます。
#include <stdio.h>
int main(void) {
double x = 0.0 / 0.0; // NaN (想定)
if (x != x) {
printf("xはNaNと判定されました (x != x)\n");
} else {
printf("xはNaNではありません\n");
}
return 0;
}xはNaNと判定されました (x != x)ただし、この方法は挙動が実装依存になる可能性もあるため、原則としてisnanの使用を推奨します。
図解で理解するNaNの比較挙動
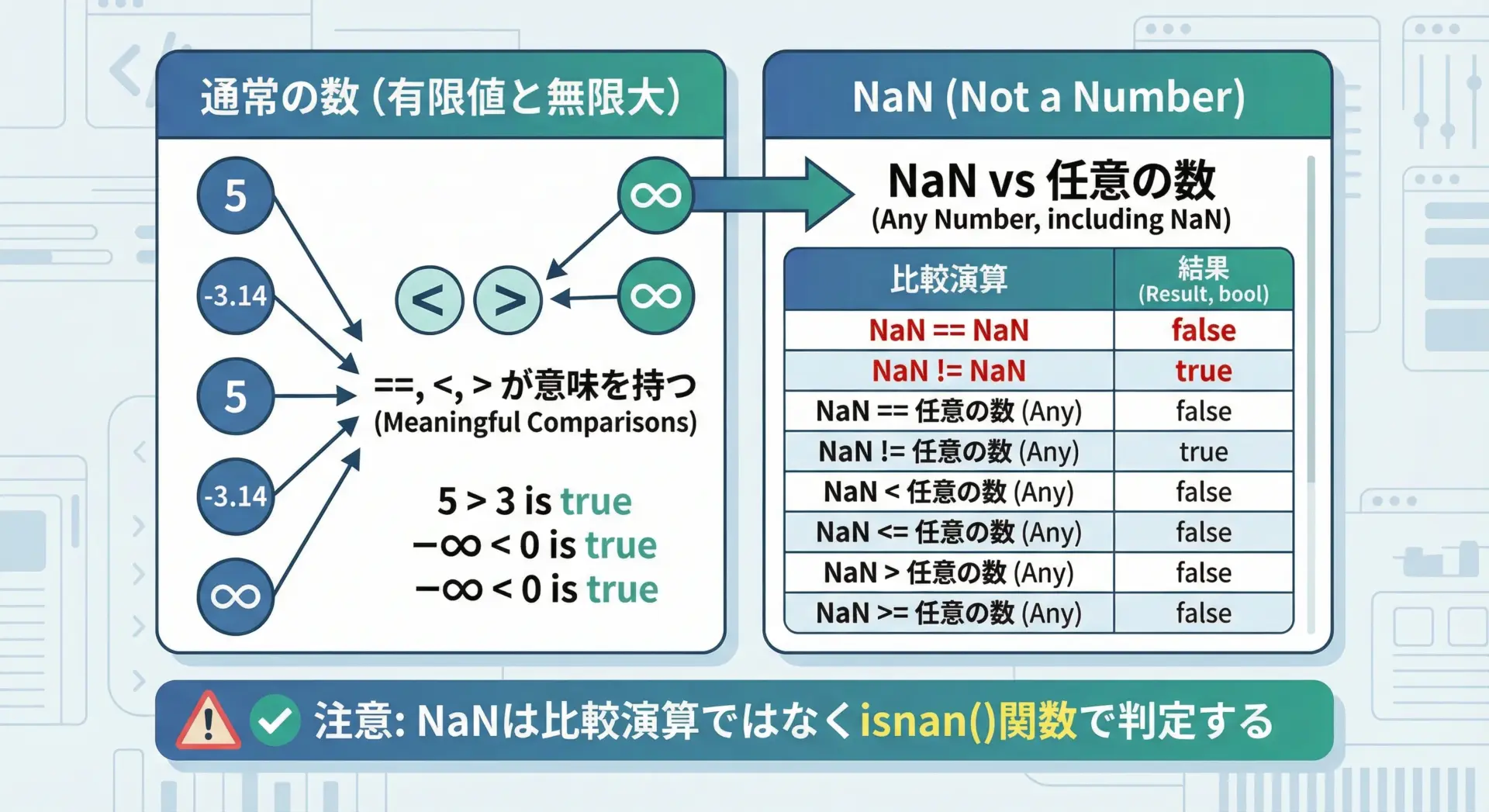
この図では、通常の数同士であれば大小比較や等価比較が意味を持つ一方、NaNが1つでも含まれた比較は「すべてfalseになる(ただし!=のみtrue)」ことを直感的に示します。
視覚的に整理しておくことで、「なぜNaNとの比較結果が期待通りにならないのか」を理解しやすくなります。
無限大・NaNと比較演算の実際
無限大の比較演算挙動
無限大同士の比較
IEEE 754を前提とすると、無限大同士は通常のルールに従って比較されます。
INFINITY == INFINITYはtrue-INFINITY == -INFINITYはtrueINFINITY > 任意の有限値はtrue-INFINITY < 任意の有限値はtrue
#include <stdio.h>
#include <math.h>
int main(void) {
double p = INFINITY;
double n = -INFINITY;
double x = 1.0;
printf("INFINITY == INFINITY : %d\n", p == INFINITY);
printf("-INFINITY == -INFINITY : %d\n", n == -INFINITY);
printf("INFINITY > 1.0 : %d\n", p > x);
printf("-INFINITY < 1.0 : %d\n", n < x);
return 0;
}INFINITY == INFINITY : 1
-INFINITY == -INFINITY : 1
INFINITY > 1.0 : 1
-INFINITY < 1.0 : 1NaNが比較に与える影響
NaNが含まれると大小比較はすべてfalse
NaNを含む比較の挙動を確認してみます。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = NAN;
double y = 1.0;
printf("x == x : %d\n", x == x);
printf("x != x : %d\n", x != x);
printf("x < y : %d\n", x < y);
printf("x > y : %d\n", x > y);
printf("x <= y : %d\n", x <= y);
printf("x >= y : %d\n", x >= y);
return 0;
}x == x : 0
x != x : 1
x < y : 0
x > y : 0
x <= y : 0
x >= y : 0NaN同士の比較も同様に、すべての大小比較はfalseになります。
ソートや最大値・最小値での注意点
NaNを含む配列のソート
浮動小数点配列をソートする際にNaNが含まれていると、比較関数が「常にfalseを返す」パターンが発生し、並べ替えアルゴリズムが想定通り動かないことがあります。
ソートの前にNaNを除外または別扱いするか、比較関数の中でisnanを用いて明示的な順序付けをすることが重要です。
比較・判定のまとめ表
無限大・NaNと比較演算の関係を表に整理します。
| 値の組み合わせ | 式 | 結果(典型例) | 説明 |
|---|---|---|---|
| 有限値 vs 有限値 | 1.0 < 2.0 | true | 通常の比較 |
| 無限大 vs 有限値 | INFINITY > 1.0 | true | 無限大は任意の有限値より大きい |
| 無限大 vs 無限大 | INFINITY == INFINITY | true | 同じ符号の無限大同士は等しい |
| NaN vs 任意の値 | x == y (NaN含む) | false | NaNとの等価比較は常にfalse |
| NaN vs 任意の値 | x != y (NaN含む) | true | != だけがtrueになる |
| NaN vs 任意の値 | x < y, x > y | false | 大小比較は意味を持たない |
NaNは「比較では判定せずisnanで判定」「無限大はisinfで判定し、必要なら比較も併用」と覚えておくと実装が安定します。
例外処理とエラー検出の考え方
IEEE 754の例外とC言語の関係
IEEE 754では、次のような例外的状況が定義されています。
- オーバーフロー
- アンダーフロー
- 無効な演算(0/0、∞−∞など)
- ゼロ除算
- 不正確(丸めにより精度が落ちる)
しかしC言語標準では、これらの例外を「例外ハンドラ」などで直接扱う仕組みは義務付けていません。
実装によってはfenv.hを使ってフラグを取得できますが、環境依存の色が濃くなります。
実用上のエラー検出パターン
1. 戻り値とerrnoを確認する(数学関数)
一部の数学関数は、エラー時にerrnoをセットします。
例としてlog関数で不正な引数を渡した場合などです。
#include <stdio.h>
#include <math.h>
#include <errno.h>
int main(void) {
errno = 0; // 事前にクリア
double x = -1.0;
double y = log(x); // log(-1) は定義されない → NaN (想定)
if (errno != 0) {
perror("log error");
}
if (isnan(y)) {
printf("結果は NaN です\n");
}
return 0;
}log error: Numerical argument out of domain
結果は NaN ですerrnoに頼るかどうかは実装やコンパイルオプションにも依存するため、ドキュメントを確認の上で併用することをおすすめします。
2. 計算結果にisnan・isinfをかける
数値計算では「重要なステップの直後でisnan・isinfによるチェックを入れる」ことがよく行われます。
#include <stdio.h>
#include <math.h>
double safe_div(double a, double b) {
double result = a / b;
if (isnan(result)) {
printf("警告: a/b の結果が NaN になりました (a=%f, b=%f)\n", a, b);
} else if (isinf(result)) {
printf("警告: a/b の結果が無限大になりました (a=%f, b=%f)\n", a, b);
}
return result;
}
int main(void) {
safe_div(1.0, 0.0); // 無限大 (想定)
safe_div(0.0, 0.0); // NaN (想定)
safe_div(1.0, 2.0); // 正常
return 0;
}警告: a/b の結果が無限大になりました (a=1.000000, b=0.000000)
警告: a/b の結果が NaN になりました (a=0.000000, b=0.000000)NaN・無限大発生時の対処戦略
戦略1: その場でエラーとして処理を中断する
クリティカルな計算では、NaNや無限大を検出した時点で即座に処理を中断し、エラーとして上位へ伝えるのが安全です。
- ログを出力し、異常値を含む入力を記録する
- エラーコードを呼び出し元に返す
- 必要ならプログラムを終了させる
戦略2: 代替値を用いて計算を継続する
リアルタイム処理やUI表示用の計算など、「停止よりも継続が優先される」場面では、以下のような代替値を用いることがあります。
- NaNを0.0に置き換える
- 無限大を上限値・下限値にクリップする
- 前回の有効な値を再利用する
#include <stdio.h>
#include <math.h>
double sanitize(double x) {
if (isnan(x)) {
return 0.0; // NaN → 0.0 に置き換え
}
if (x > 1e6) { // 上限を設定
return 1e6;
}
if (x < -1e6) { // 下限を設定
return -1e6;
}
return x; // 問題なし
}
int main(void) {
double values[] = { NAN, INFINITY, -INFINITY, 100.0 };
size_t n = sizeof(values) / sizeof(values[0]);
for (size_t i = 0; i < n; i++) {
double s = sanitize(values[i]);
printf("raw=%f, sanitized=%f\n", values[i], s);
}
return 0;
}raw=nan, sanitized=0.000000
raw=inf, sanitized=1000000.000000
raw=-inf, sanitized=-1000000.000000
raw=100.000000, sanitized=100.000000どの戦略を採用するかは、アプリケーションの要件と安全性のバランスを考慮して決める必要があります。
実践的なサンプルコード集
入力値の検証付き計算関数
例: 安全な平方根関数
#include <stdio.h>
#include <math.h>
// 入力値を検証しながら平方根を計算する関数
// 戻り値: 正常な場合 0、異常な場合 非0
int safe_sqrt(double x, double *out_result) {
if (x < 0.0) {
// 負の数の平方根は定義されない
fprintf(stderr, "エラー: 負の入力に対するsqrt(x)です (x=%f)\n", x);
*out_result = NAN;
return -1;
}
double r = sqrt(x);
if (isnan(r) || isinf(r)) {
fprintf(stderr, "エラー: sqrtの結果がNaNまたは無限大です (x=%f)\n", x);
*out_result = NAN;
return -2;
}
*out_result = r;
return 0;
}
int main(void) {
double inputs[] = { 4.0, -1.0, INFINITY };
size_t n = sizeof(inputs) / sizeof(inputs[0]);
for (size_t i = 0; i < n; i++) {
double x = inputs[i];
double r;
int err = safe_sqrt(x, &r);
if (err == 0) {
printf("sqrt(%f) = %f\n", x, r);
} else {
printf("sqrt(%f) に失敗しました (err=%d)\n", x, err);
}
}
return 0;
}sqrt(4.000000) = 2.000000
エラー: 負の入力に対するsqrt(x)です (x=-1.000000)
sqrt(-1.000000) に失敗しました (err=-1)
エラー: sqrtの結果がNaNまたは無限大です (x=inf)
sqrt(inf) に失敗しました (err=-2)この例では、入力値に対する事前検証と結果に対する事後検証を両方行うことで、安全なインターフェースを構成しています。
配列内のNaN・無限大を検出するユーティリティ
#include <stdio.h>
#include <math.h>
// 配列内にNaNまたは無限大が含まれているか調べる
int has_nan_or_inf(const double *arr, size_t n) {
for (size_t i = 0; i < n; i++) {
if (isnan(arr[i]) || isinf(arr[i])) {
return 1; // 見つかった
}
}
return 0; // 見つからなかった
}
int main(void) {
double a[] = { 1.0, 2.0, 3.0 };
double b[] = { 1.0, NAN, 3.0 };
double c[] = { 1.0, INFINITY, 3.0 };
printf("a: %d\n", has_nan_or_inf(a, 3));
printf("b: %d\n", has_nan_or_inf(b, 3));
printf("c: %d\n", has_nan_or_inf(c, 3));
return 0;
}a: 0
b: 1
c: 1このような簡易チェック関数を用意しておけば、大量のデータを扱う前に「安全性チェック」を一括で実行できます。
JSONやテキスト出力時にNaN・無限大を文字列に変換
多くのフォーマット(JSONなど)では、NaNや無限大をそのまま数値として書き出すと非標準な表現になってしまいます。
そのため、文字列に変換して扱う方法がよく利用されます。
#include <stdio.h>
#include <math.h>
void print_value_for_json(double x) {
if (isnan(x)) {
printf("\"NaN\"");
} else if (isinf(x)) {
if (x > 0) {
printf("\"Infinity\"");
} else {
printf("\"-Infinity\"");
}
} else {
printf("%f", x);
}
}
int main(void) {
double values[] = { 1.23, NAN, INFINITY, -INFINITY };
size_t n = sizeof(values) / sizeof(values[0]);
printf("[");
for (size_t i = 0; i < n; i++) {
if (i > 0) printf(", ");
print_value_for_json(values[i]);
}
printf("]\n");
return 0;
}["1.230000", "NaN", "Infinity", "-Infinity"]この例では単純なJSON風表現ですが、アプリケーション間で数値をやり取りする際にNaN・無限大をどう表現するかを事前に取り決めることが重要です。
まとめ
C言語の無限大とNaNは、一見すると特殊で難解に感じられますが、IEEE 754という決めごとに従っている「状態付きの浮動小数点値」だと理解すると整理しやすくなります。
無限大は「範囲外に発散した値」、NaNは「数として意味を持たない結果」を表現し、それぞれisinf・isnanで判定します。
特にNaNは比較演算では正しく検出できないため、必ず専用の判定関数を使うことが重要です。
数値計算やデータ処理では、重要な演算直後にNaN・無限大をチェックし、ログ出力や代替値への置き換えなどの方針を一貫して適用することで、バグの早期発見と信頼性向上につながります。
本記事を参考に、無限大とNaNを正しく扱える堅牢なCプログラムを設計してみてください。

