コンピュータで小数を扱うと、思わぬ誤差やバグが発生することがあります。
C言語では、その原因の多くが浮動小数点数の表現方式や桁数の限界にあります。
本記事では、浮動小数点の精度問題を防ぐために、標準ヘッダfloat.hをどう活用すべきかを、実践的なテクニックとサンプルコードで詳しく解説します。
浮動小数点の基本と精度問題の正体
浮動小数点とは何か
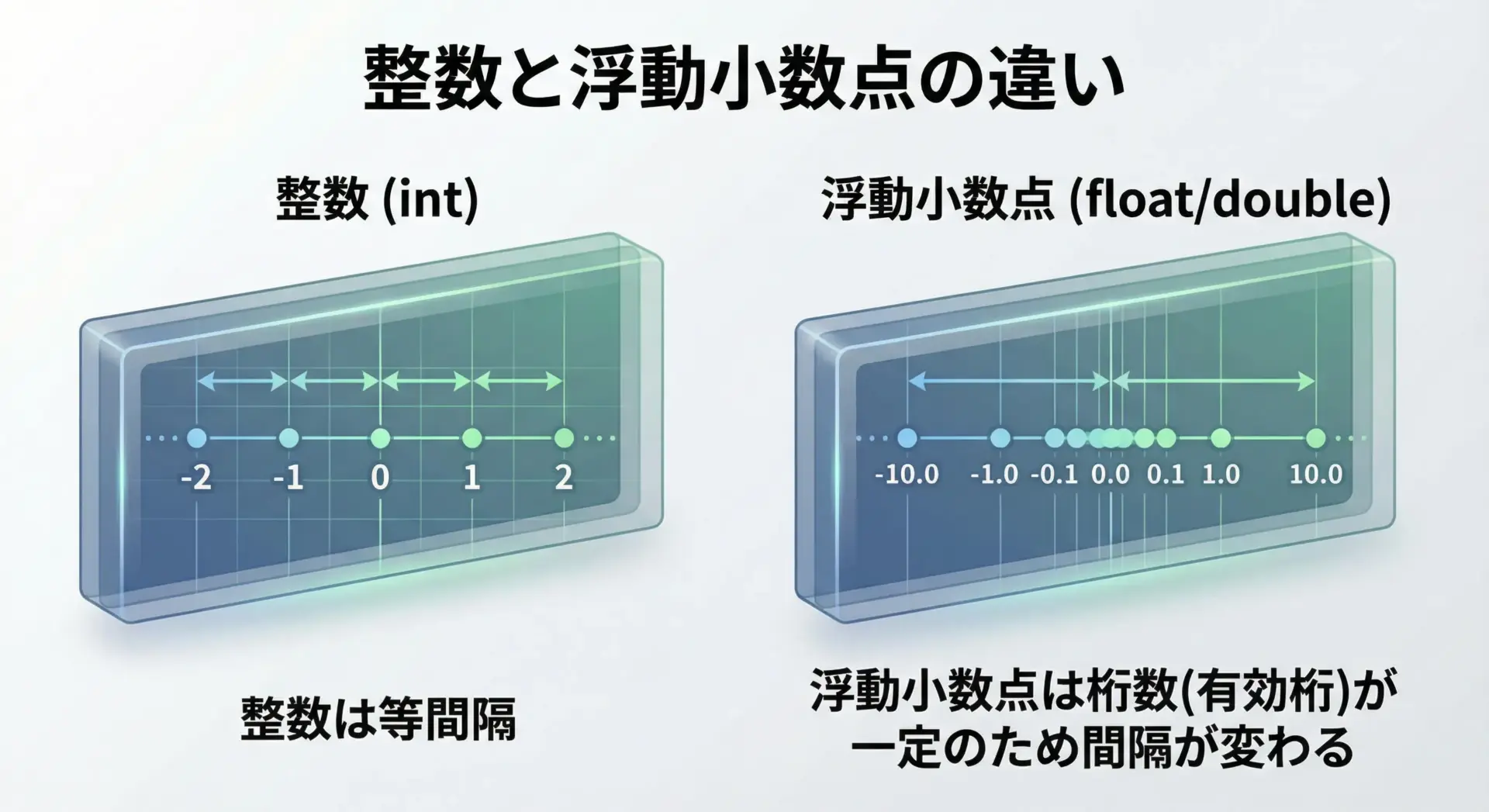
浮動小数点数は、実数を「仮数部」と「指数部」に分けて表現する方式です。
C言語では、IEEE 754準拠の形式が使われることが多く、floatやdoubleは、2進数の科学技術表記に近い形で値を保持します。
整数型が「1ずつきっちり並んだ値」を表現できるのに対し、浮動小数点数は表現できる数値の位置が不均一で、桁数(有効数字)に上限があるという特徴があります。
この性質こそが、精度問題の原因となります。
なぜ誤差が発生するのか
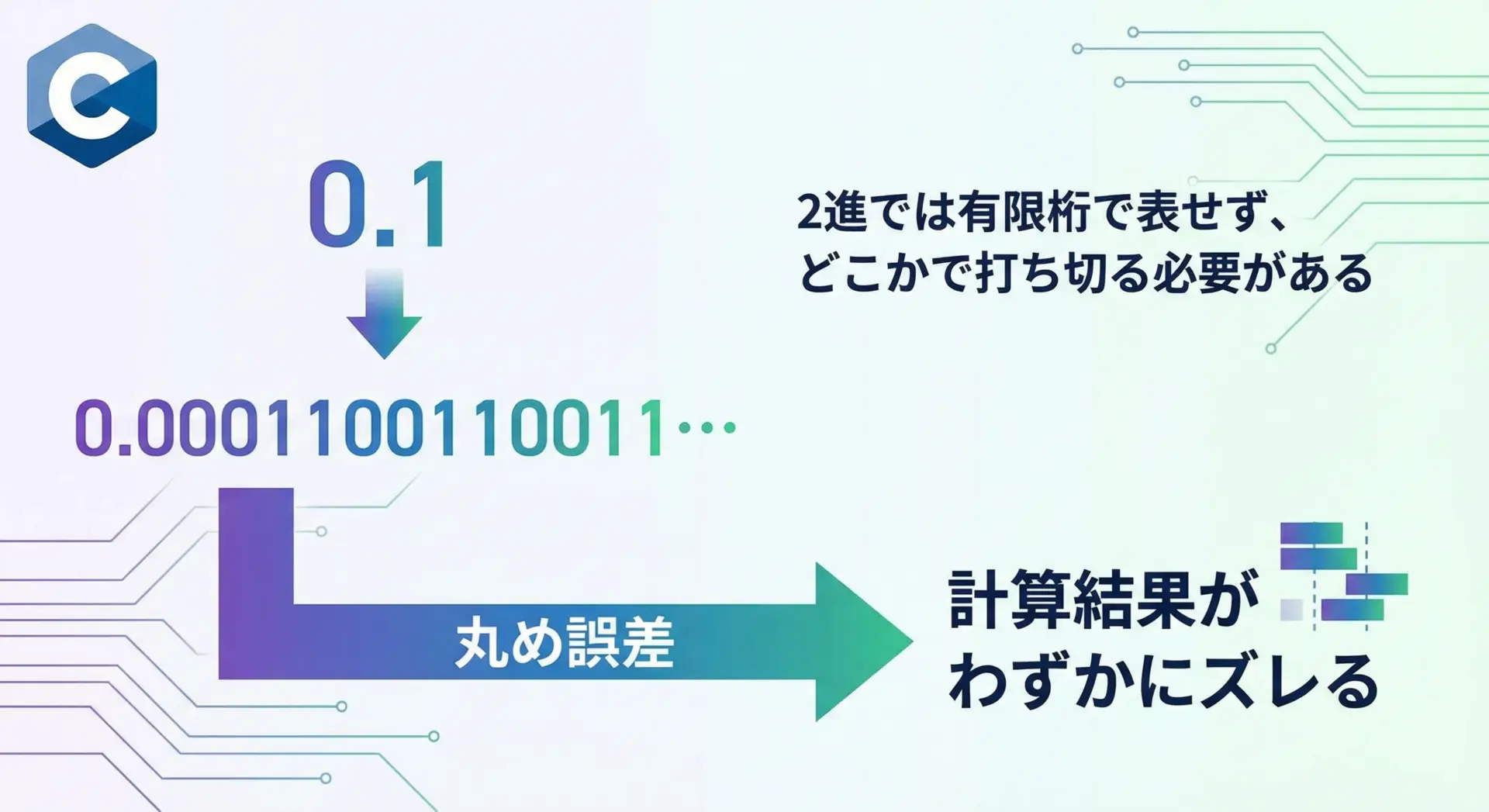
たとえば、10進数の0.1は、2進数では有限桁で正確に表現できません。
そのため、コンピュータ内部では「0.1に非常に近いが、完全には一致しない値」が保存されます。
これが丸め誤差です。
この誤差が積み重なると、次のような現象が起きます。
- 期待した値と
==で比較しても一致しない - 長いループ計算で、合計値が少しずつズレる
- 14に見える値を表示すると、3.1400000000000001のようになる
浮動小数点の計算は、数学的な実数の計算と完全には一致しないという前提で設計する必要があります。
float.hで取得できる「浮動小数点の限界」
float.hとは
C言語のfloat.hは、実装依存の浮動小数点の制限や特性を定数として提供するヘッダです。
つまり、「この環境ではfloatは何桁まで正確に扱えるのか」「どれくらい小さい数まで扱えるのか」といった情報を、ポータブルに取得できます。
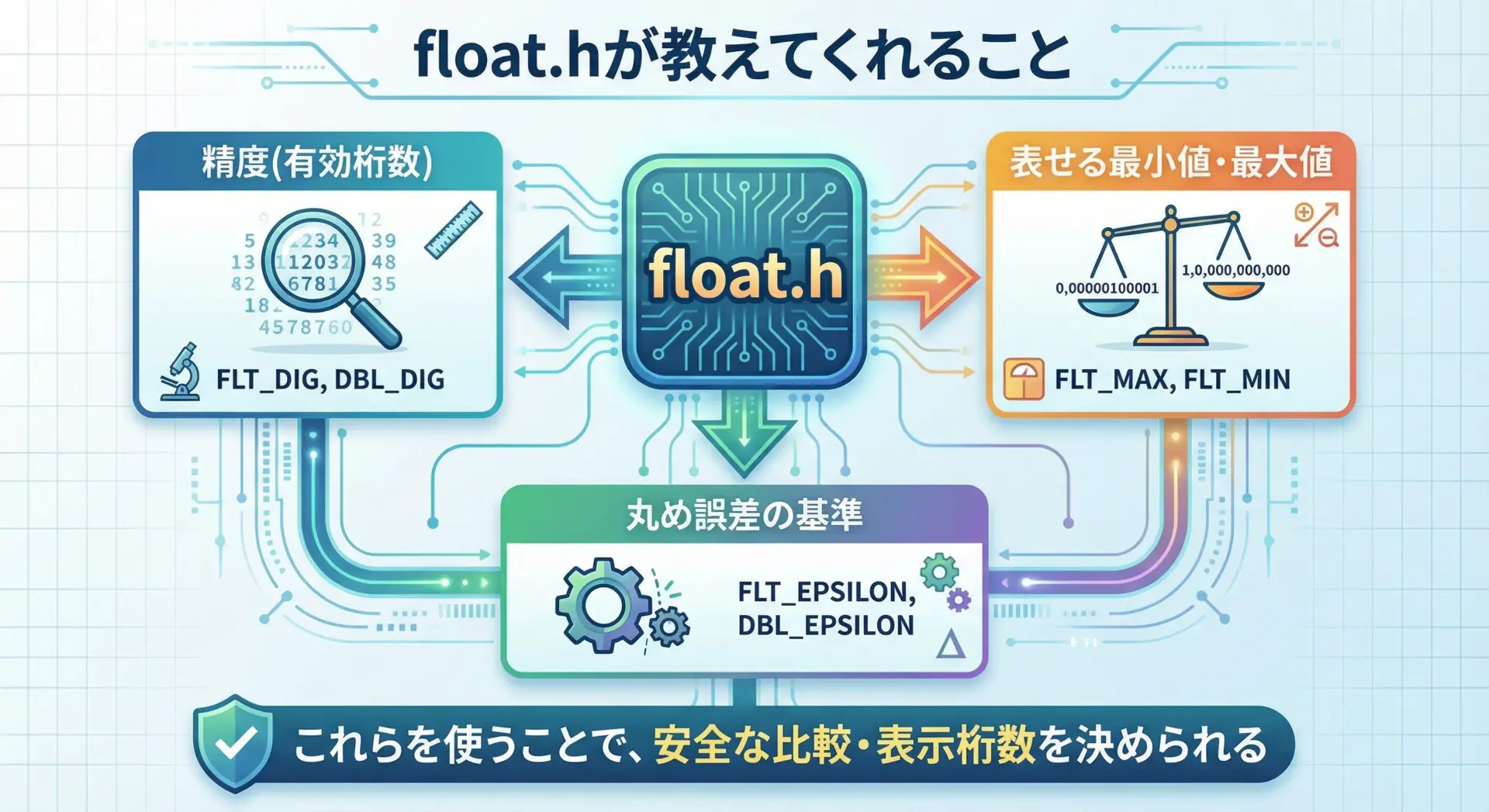
このヘッダを活用することで、環境に依存しない精度の扱い方を記述できるようになります。
主なマクロ一覧と意味
以下に代表的なマクロを示します。
| マクロ名 | 対象型 | 意味(概要) |
|---|---|---|
| FLT_DIG | float | 10進で保証される有効数字の最大桁数 |
| DBL_DIG | double | 同上( double版 ) |
| LDBL_DIG | long double | 同上( long double版 ) |
| FLT_EPSILON | float | 1.0と区別できる最小の差(機械イプシロン) |
| DBL_EPSILON | double | 同上( double版 ) |
| FLT_MIN | float | 規格化された最小の正の値 |
| FLT_MAX | float | 最大の有限正数 |
| FLT_MANT_DIG | float | 基数表現における仮数部のビット数 |
| FLT_MAX_10_EXP | float | 10の指数として取りうる最大値(10進表現の最大桁の目安) |
| FLT_MIN_10_EXP | float | 10の指数として取りうる最小値 |
精度に直接関係するのは、DIGとEPSILONです。
これらを理解し、プログラムに組み込むことで、誤差を意識した安全な設計が可能になります。
有効数字(DIG)を理解して安全な表示桁数を決める
FLT_DIG / DBL_DIG の意味

FLT_DIGは、「floatが10進でどのくらいの桁数まで正確であると保証されるか」を示すマクロです。
たとえば、ほとんどの環境ではFLT_DIGは6であり、「10進有効数字6桁までは安全に扱える」ことを意味します。
DBL_DIGはdouble版で、通常は15程度です。
したがって、printfでの表示桁数は、DIGを超えないようにするのが、見た目と内部値の乖離を避ける基本テクニックとなります。
DIGを使って安全なprintfフォーマットを決める
次のサンプルでは、floatとdoubleのDIGを取得し、その桁数に合わせて出力する方法を示します。
#include <stdio.h>
#include <float.h>
int main(void) {
float f = 1.0f / 3.0f;
double d = 1.0 / 3.0;
// FLT_DIG, DBL_DIGを表示
printf("FLT_DIG = %d\n", FLT_DIG);
printf("DBL_DIG = %d\n", DBL_DIG);
// 安全とされる桁数(有効数字)で表示
printf("\nfloat を FLT_DIG 桁で表示:\n");
// %.6g のように、%g は有効数字の桁数指定になる
printf("f = %.*g\n", FLT_DIG, f);
printf("\ndouble を DBL_DIG 桁で表示:\n");
printf("d = %.*g\n", DBL_DIG, d);
// あえてDIGを超える桁数で表示してみる
printf("\nDIG を超える桁数での表示例:\n");
printf("float (15桁) = %.15f\n", f);
printf("double (20桁) = %.20f\n", d);
return 0;
}FLT_DIG = 6
DBL_DIG = 15
float を FLT_DIG 桁で表示:
f = 0.333333
double を DBL_DIG 桁で表示:
d = 0.333333333333333
DIG を超える桁数での表示例:
float (15桁) = 0.333333343267440
double (20桁) = 0.33333333333333331483DIG以内の表示では、見た目上の違和感が少ないのに対し、DIGを超えた桁を表示すると、内部で保持している近似値の「ズレ」が露わになります。
ユーザ向け表示はDIG以内、内部デバッグ用ではあえて長桁を出すといった使い分けが重要です。
EPSILONを使った「誤差を踏まえた比較」テクニック
FLT_EPSILON / DBL_EPSILON とは
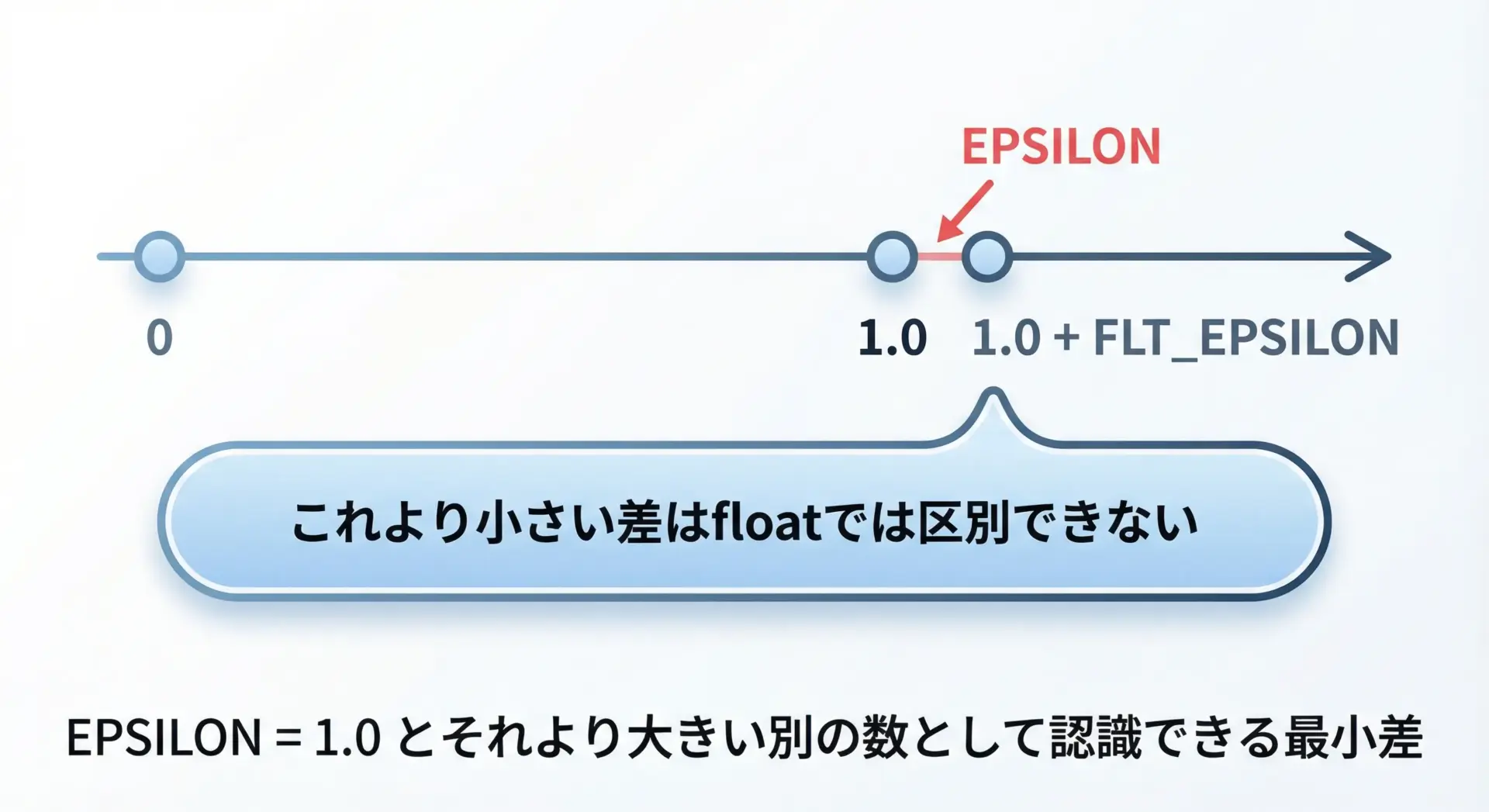
FLT_EPSILONは、float型において「1.0」と区別できる最小の差を表します。
つまり、1.0f + FLT_EPSILONは1.0fとは違う数として認識されますが、1.0f + FLT_EPSILON / 2は丸めの結果として1.0fと区別できない場合があります。
この性質を利用し、浮動小数点数同士を「ぴったり一致」で比較する代わりに、「EPSILONを基準にした許容誤差内に収まっているか」で判断するのが定石です。
単純な==比較が危険な例
#include <stdio.h>
int main(void) {
float a = 0.1f * 3.0f; // 0.3 のつもり
float b = 0.3f;
printf("a = %.10f\n", a);
printf("b = %.10f\n", b);
if (a == b) {
printf("a == b です\n");
} else {
printf("a != b です\n");
}
return 0;
}a = 0.3000000119
b = 0.3000000119
a == b です上記はたまたま等しくなりましたが、計算パスやコンパイラ最適化によってはa == bが偽になることもあり得ます。
別のパターンも見てみます。
#include <stdio.h>
int main(void) {
float a = 0.1f;
float b = 0.0f;
for (int i = 0; i < 3; i++) {
b += 0.1f; // 0.1 を3回足して 0.3 のつもり
}
printf("a*3 = %.10f\n", a * 3.0f);
printf("b = %.10f\n", b);
if (a * 3.0f == b) {
printf("a*3 == b です\n");
} else {
printf("a*3 != b です\n");
}
return 0;
}a*3 = 0.3000000119
b = 0.3000000119
a*3 == b ですこの例も値が同じになっていますが、演算順序や最適化によって、微妙に異なる値となることがあります。
「常に==で比較してよい」とは決して言えないのがポイントです。
EPSILONを使った「ほぼ等しい」判定
浮動小数点数を比較するときは、絶対値の差が十分小さいかどうかで判断します。
その基準として、型に応じたEPSILONを利用します。
#include <stdio.h>
#include <math.h>
#include <float.h>
// float用の「ほぼ等しい」判定関数
int float_almost_equal(float x, float y) {
// 絶対値の差が、floatのEPSILONの数倍以内なら等しいとみなす
float diff = fabsf(x - y);
float eps = FLT_EPSILON * 10.0f; // 安全側にやや広げる
return diff <= eps;
}
// double用の「ほぼ等しい」判定関数(参考)
int double_almost_equal(double x, double y) {
double diff = fabs(x - y);
double eps = DBL_EPSILON * 10.0;
return diff <= eps;
}
int main(void) {
float a = 0.1f;
float b = 0.0f;
for (int i = 0; i < 3; i++) {
b += 0.1f;
}
float c = a * 3.0f;
printf("b = %.10f\n", b);
printf("c = %.10f\n", c);
printf("\n単純な比較:\n");
printf("b == c ? %s\n", (b == c) ? "true" : "false");
printf("\nEPSILON を用いた比較:\n");
printf("float_almost_equal(b, c) ? %s\n",
float_almost_equal(b, c) ? "true" : "false");
return 0;
}b = 0.3000000119
c = 0.3000000119
単純な比較:
b == c ? true
EPSILON を用いた比較:
float_almost_equal(b, c) ? trueこの例ではどちらもtrueですが、設計として「EPSILONを考慮した比較関数を用意しておく」ことが重要です。
EPSILONの倍率は用途に応じて調整し、「どの程度の誤差なら許容できるか」を仕様として明確にする必要があります。
float.hを活用した「オーバーフロー・アンダーフロー対策」
FLT_MAX / FLT_MIN で範囲チェックを行う

FLT_MAXとFLT_MINは、float型で扱える規格化数の最大値と最小値です。
大きな数値計算を行う際には、計算前に範囲をチェックしておくことで、不意のオーバーフローやアンダーフローを避けられます。
#include <stdio.h>
#include <float.h>
#include <math.h>
int main(void) {
float x = FLT_MAX / 2.0f;
float y = 3.0f;
printf("FLT_MAX = %e\n", FLT_MAX);
printf("x = %e\n", x);
printf("y = %e\n", y);
// 掛け算の前にオーバーフローしないかを判定
if (fabsf(x) > FLT_MAX / fabsf(y)) {
printf("\n警告: x * y はオーバーフローする可能性があります\n");
} else {
float z = x * y;
printf("\nz = x * y = %e\n", z);
}
return 0;
}FLT_MAX = 3.402823e+38
x = 1.701412e+38
y = 3.000000e+00
警告: x * y はオーバーフローする可能性があります演算前に最大値で割って境界を確認することで、安全に範囲チェックを行っています。
特に物理シミュレーションや金融計算など、値が大きくなりがちな処理では有効です。
実務で役立つfloat.h×精度対策パターン集
パターン1: 出力フォーマットを型に応じて自動調整
「floatかdoubleかでprintfの桁数を変える」ユーティリティを用意しておくと、ライブラリや共有コードで便利です。
#include <stdio.h>
#include <float.h>
// float 用の標準フォーマット(有効数字ベース)
void print_float_auto(float x) {
printf("%.*g", FLT_DIG, x);
}
// double 用の標準フォーマット
void print_double_auto(double x) {
printf("%.*g", DBL_DIG, x);
}
int main(void) {
float f = 1.0f / 7.0f;
double d = 1.0 / 7.0;
printf("float : ");
print_float_auto(f);
printf("\n");
printf("double : ");
print_double_auto(d);
printf("\n");
return 0;
}float : 0.142857
double : 0.142857142857143型に合わせてDIGを使うことで、「その型で保証される有効数字だけを表示する」ことができます。
パターン2: 安全な「ほぼゼロ」判定
数値が「ゼロかどうか」を判定したい場面も多くありますが、ここでも==0.0は危険です。
EPSILONを基準にしたゼロ判定を行います。
#include <stdio.h>
#include <math.h>
#include <float.h>
// float 用の「ほぼゼロ」判定
int float_is_almost_zero(float x) {
return fabsf(x) <= FLT_EPSILON;
}
int main(void) {
float x = 1.0f;
for (int i = 0; i < 30; i++) {
x /= 2.0f; // 何度も2で割ると、やがて非常に小さな値になる
}
printf("x = %.30f\n", x);
if (x == 0.0f) {
printf("x は 0.0f と完全に等しい\n");
} else {
printf("x は 0.0f ではない(ビット的には非ゼロ)\n");
}
if (float_is_almost_zero(x)) {
printf("float_is_almost_zero(x) によれば、ほぼゼロとみなせます\n");
} else {
printf("float_is_almost_zero(x) によれば、まだゼロとはみなせません\n");
}
return 0;
}x = 0.000000000000000888178419700125
x は 0.0f ではない(ビット的には非ゼロ)
float_is_almost_zero(x) によれば、ほぼゼロとみなせます数学的には「ほとんどゼロ」と見なせる値でも、ビットとしては非ゼロであることが多くあります。
このようなケースでは、EPSILONベースの判定が有効です。
パターン3: 計算誤差を抑えるための再配置とスケーリング
float.hの情報と組み合わせて、計算順序の見直しやスケーリングを行うことで、誤差を抑えやすくなります。
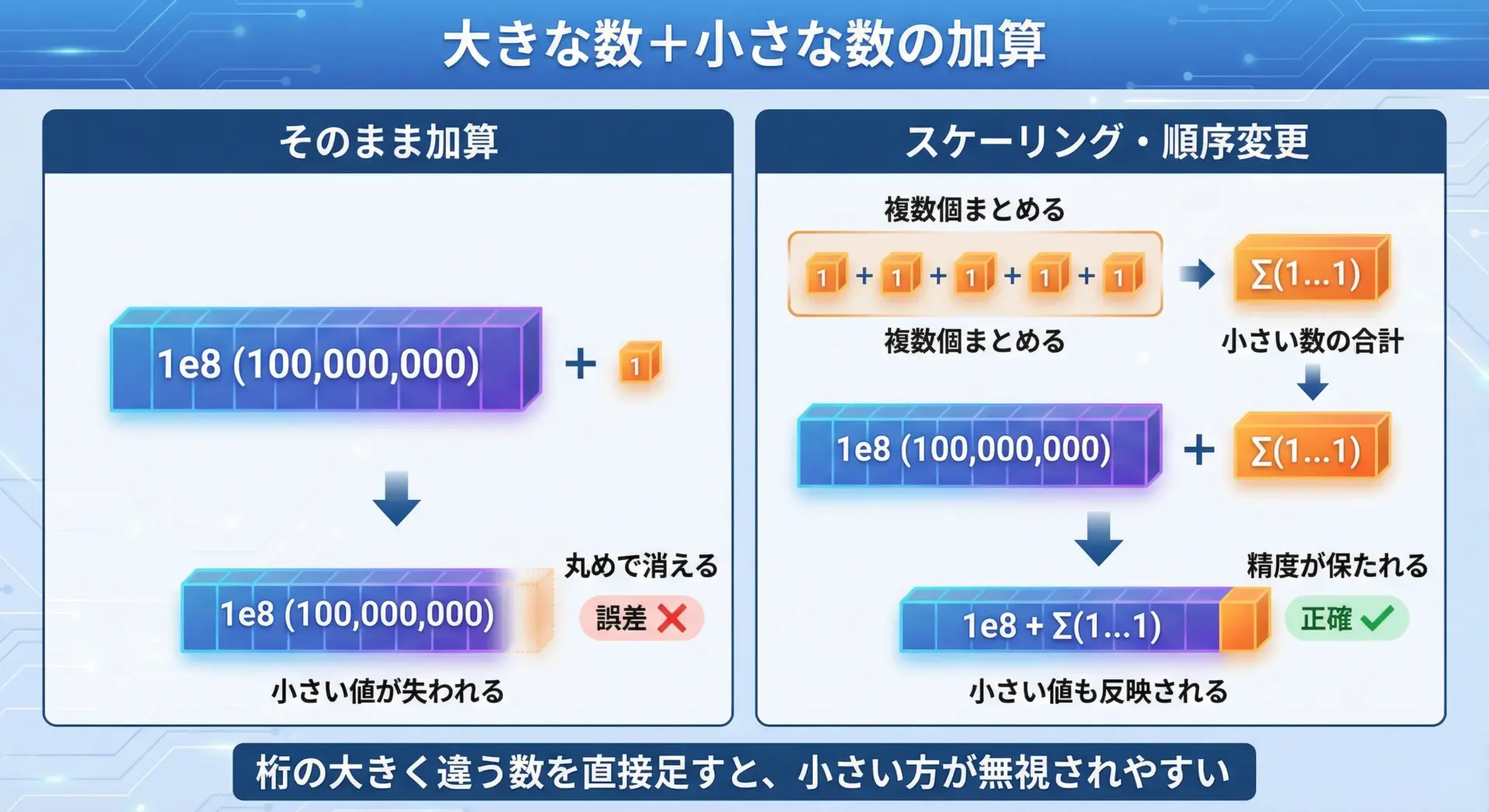
たとえば、非常に大きな値と非常に小さな値を足すと、小さい方が丸めで消えてしまうことがあります。
これを避けるには、値をスケールして桁を近づけるか、小さい値同士を先にまとめてから加算するなどの工夫が必要です。
#include <stdio.h>
#include <math.h>
int main(void) {
double big = 1e12;
double sum1 = big;
double sum2 = 0.0;
// small を何度も big に直接加算
double small = 1.0;
for (int i = 0; i < 1000000; i++) {
sum1 += small;
}
// small 同士を先にまとめてから big に加算
for (int i = 0; i < 1000000; i++) {
sum2 += small;
}
sum2 += big;
printf("sum1 (big に直接 small を加算) = %.0f\n", sum1);
printf("sum2 (small 同士を先に加算) = %.0f\n", sum2);
return 0;
}sum1 (big に直接 small を加算) = 1000000000000
sum2 (small 同士を先に加算) = 1000001000000同じ演算でも、順序によって結果が変わる典型的な例です。
doubleでもこのような差が出るため、floatではなおさら慎重な設計が必要です。
float.hの情報から型の限界を把握し、「どの程度の桁まで意味があるか」を意識しながらアルゴリズムを組み立てることが大切です。
floatとdoubleの選び方とfloat.hによる裏付け
なぜfloatではなくdoubleを推奨されることが多いのか
多くの実務では、floatよりdoubleが推奨されます。
その理由の1つがDBL_DIGとFLT_DIGの差です。
| 型 | 一般的なサイズ | DIG(有効数字) | 用途のイメージ |
|---|---|---|---|
| float | 32ビット | 6〜7桁 | メモリ節約が重要な大量データ、GPU計算など |
| double | 64ビット | 15〜16桁 | 一般的な数値計算、業務アプリケーション |
doubleはfloatの約2倍以上の有効桁数を持っており、誤差の蓄積に対してかなり余裕があります。
float.hで実際のFLT_DIGとDBL_DIGを確認し、「この問題ならfloatで十分か」を判断するのが実践的です。
float.hで環境依存を吸収する

C言語標準は、floatやdoubleの具体的なビット数を完全には固定していません。
そのため、組込み環境などではPCと異なる特性を持つこともあります。
float.hを使ってその環境の特性をプログラムから取得することで、ポータブルなコード設計が可能になります。
例として、起動時に環境情報をログ出力するコードを示します。
#include <stdio.h>
#include <float.h>
void print_float_env_info(void) {
printf("=== float / double 環境情報 ===\n");
printf("float : DIG = %d, EPSILON = %e, MIN = %e, MAX = %e\n",
FLT_DIG, FLT_EPSILON, FLT_MIN, FLT_MAX);
printf("double: DIG = %d, EPSILON = %e, MIN = %e, MAX = %e\n",
DBL_DIG, DBL_EPSILON, DBL_MIN, DBL_MAX);
printf("================================\n");
}
int main(void) {
print_float_env_info();
return 0;
}=== float / double 環境情報 ===
float : DIG = 6, EPSILON = 1.192093e-07, MIN = 1.175494e-38, MAX = 3.402823e+38
double: DIG = 15, EPSILON = 2.220446e-16, MIN = 2.225074e-308, MAX = 1.797693e+308
================================このように環境に応じた数値特性をログに残しておくと、後からバグ調査を行う際にも有用です。
まとめ
浮動小数点は、実数を近似的に扱うための強力な仕組みですが、「無限の精度があるわけではない」という前提を理解せずに使うと、思わぬ誤差やバグの原因になります。
本記事では、float.hが提供するDIGやEPSILON、MIN/MAXなどの情報を活用し、精度問題を抑える実践テクニックを解説しました。
ポイントは、有効数字を意識した表示桁数の制御と、EPSILONを用いた「ほぼ等しい」比較、そして範囲チェックと計算順序の工夫です。
これらを組み合わせることで、より堅牢で信頼性の高い数値処理コードをC言語で実現できるようになります。

