C言語で乱数を扱うとき、「0〜n-1の整数」だけでなく「任意の最小値~最大値」の範囲で思い通りに乱数を出したくなる場面は多いです。
本記事では、C言語での乱数の基本から、整数・浮動小数点・負の数を含む範囲指定、さらに偏りを抑えた実践的なテクニックまでを、図解とサンプルコード付きで丁寧に解説します。
C言語の乱数の基本を理解しよう
C言語標準の乱数関数rand()とは

C言語の標準ライブラリには、擬似乱数を生成するrand()関数が用意されています。
擬似乱数という言葉が示す通り、完全なランダムではなく、ある規則に基づいて生成される乱数列ですが、多くの用途では十分実用的です。
rand()は、次のような仕様を持っています。
- 返り値の型は
int - 返される値の範囲は
0以上RAND_MAX以下 RAND_MAXはstdlib.hで定義されるマクロで、多くの処理系では32767や2147483647など
つまりrand()は、「0~RAND_MAXの間の整数乱数」を1つ返す関数です。
このままでは範囲の指定ができないため、後述するテクニックで%演算子やスケーリングを行い、目的の範囲にマッピングします。
シード値srand()で乱数列を変える
rand()は内部に状態(シード値)を持ち、その状態から乱数列を生成します。
実行ごとに異なる乱数列を得るには、srand()で初期化する必要があります。
最もよく使われるのは、time(NULL)を用いた初期化です。
#include <stdio.h>
#include <stdlib.h> // rand, srand
#include <time.h> // time
int main(void) {
// 現在時刻をシード(種)として乱数列を初期化
srand((unsigned int)time(NULL));
// 乱数を5回表示
for (int i = 0; i < 5; i++) {
int r = rand(); // 0~RAND_MAXの整数
printf("%d\n", r);
}
return 0;
}(実行例・出力は環境により異なる)
1804289383
846930886
1681692777
1714636915
1957747793同じプログラムを同じ時刻に実行すると同じ列、異なる時刻に実行すれば異なる列になります。
デバッグのために乱数列を再現したい場合は、srand(1234)のように固定値を使う方法も有効です。
乱数の範囲指定の基本パターン
0~n-1の乱数を生成する
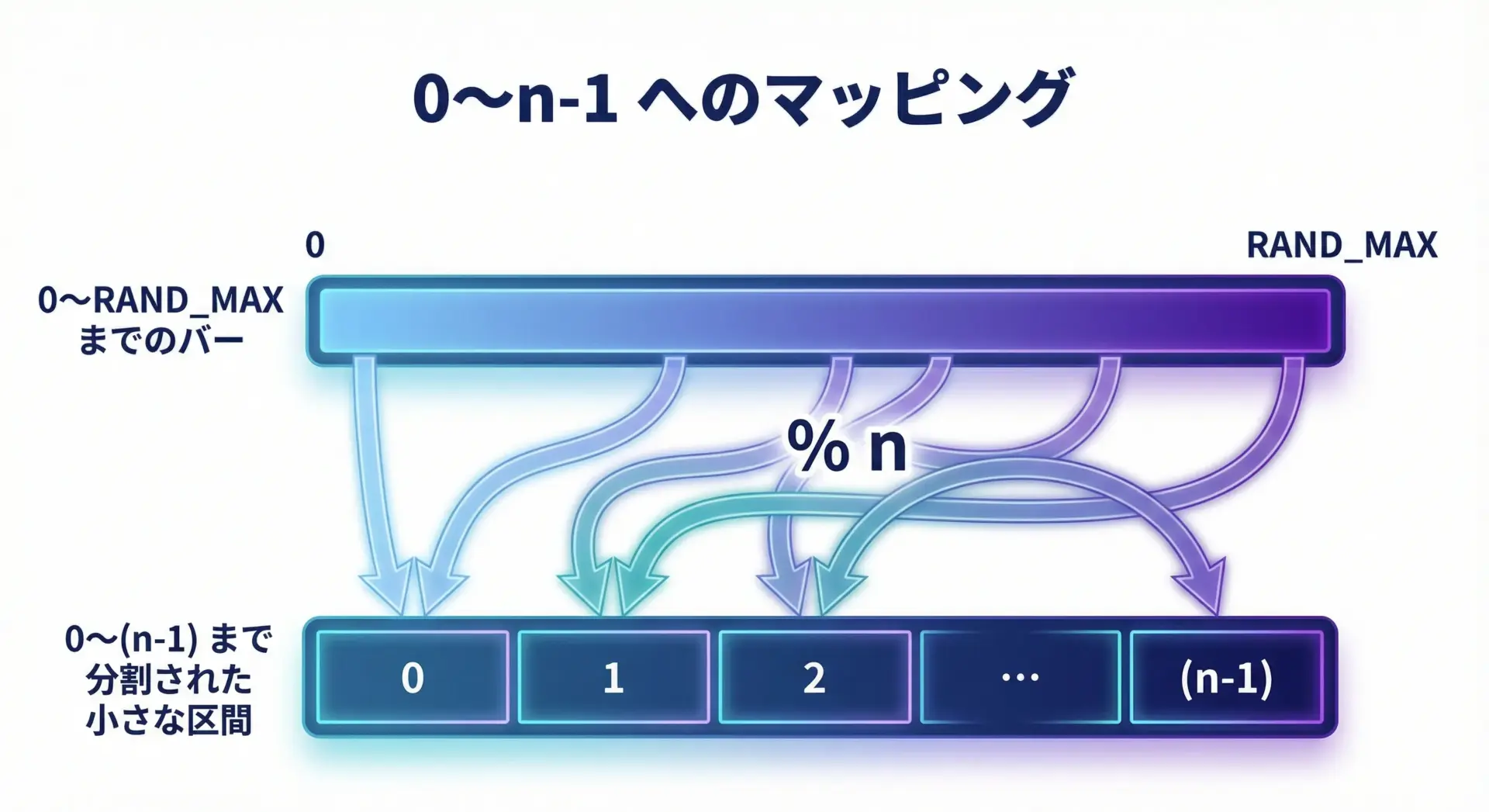
最も基本的な範囲指定は、0以上n未満の整数乱数を生成する方法です。
これはrand()の結果に%演算子(剰余)を適用することで実現できます。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void) {
srand((unsigned int)time(NULL));
int n = 6; // 0~5までの範囲を例にする
for (int i = 0; i < 10; i++) {
int r = rand() % n; // 0 ~ n-1 の乱数
printf("%d ", r);
}
printf("\n");
return 0;
}(実行例)
3 0 5 1 2 1 4 0 3 5この方法は簡単ですが、後で説明するように厳密な一様分布を必要とする場合には偏りが出る可能性があります。
ただし、簡易的な用途(サイコロ風の表示、テストデータなど)であれば、まずはこの形を覚えておくと便利です。
最小値~最大値の整数乱数を生成する
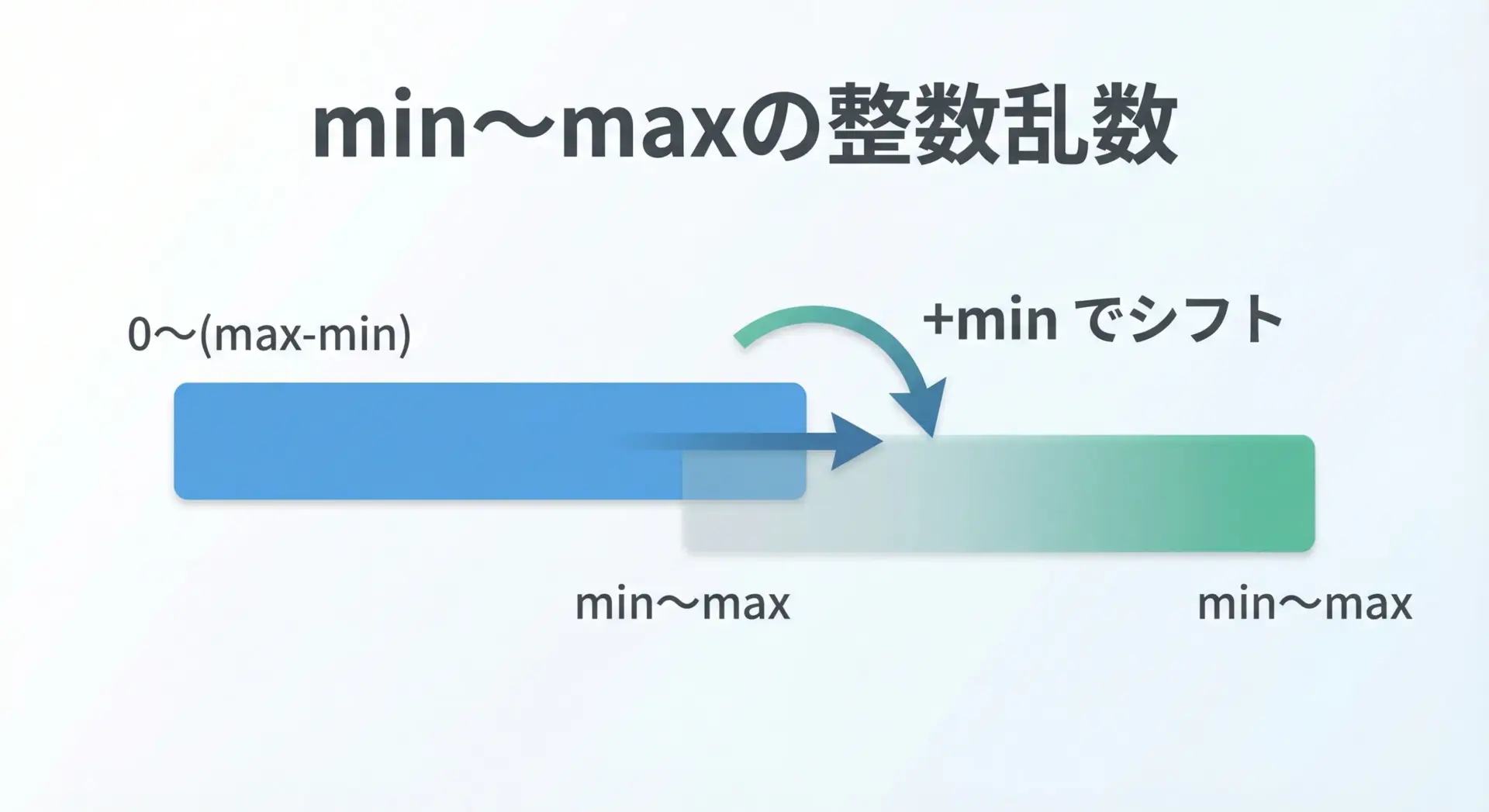
0~n-1から一歩進んで、任意の最小値min~最大値maxまでの範囲を扱えるようにします。
考え方はシンプルで、次の2段階で処理します。
- 幅を求める:
range = max - min + 1 0~range-1の乱数を作り、それにminを足す
コードにすると次のようになります。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// min~max の範囲で整数乱数を返す関数
int rand_range_int(int min, int max) {
if (min > max) {
// 引数が逆転していた場合は入れ替える(簡易防御策)
int tmp = min;
min = max;
max = tmp;
}
int range = max - min + 1; // 取りうる値の個数
int r = rand() % range; // 0 ~ range-1
return min + r; // min ~ max
}
int main(void) {
srand((unsigned int)time(NULL));
int min = 10;
int max = 20;
for (int i = 0; i < 10; i++) {
int v = rand_range_int(min, max);
printf("%d ", v);
}
printf("\n");
return 0;
}(実行例)
17 20 11 13 10 18 14 19 12 16この関数を用意しておけば、rand_range_int(-5, 5)のように負の数を含む範囲でも、簡単に指定できます。
範囲指定を使った実践サンプル
サイコロ(1~6)の乱数を作る
サイコロの出目は1~6なので、先ほどの関数をそのまま応用できます。
簡易版として、関数を使わない形も示します。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void) {
srand((unsigned int)time(NULL));
for (int i = 0; i < 10; i++) {
// 1~6の乱数 (サイコロの出目)
int dice = (rand() % 6) + 1;
printf("%d ", dice);
}
printf("\n");
return 0;
}(実行例)
4 1 6 2 5 3 2 6 1 5「0~5の乱数を作って、それに1を足す」というパターンが、1~6のサイコロ以外にもさまざまな場面で応用できます。
配列の要素をランダムに選ぶ

配列からランダムな要素を1つ取り出したい場合は、0~(配列長-1)の乱数を添字として使えばよいです。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
int main(void) {
const char *colors[] = {
"Red", "Green", "Blue", "Yellow", "Purple"
};
int len = (int)(sizeof(colors) / sizeof(colors[0]));
srand((unsigned int)time(NULL));
for (int i = 0; i < 5; i++) {
int index = rand() % len; // 0~len-1 のランダムな添字
printf("Selected color: %s\n", colors[index]);
}
return 0;
}(実行例)
Selected color: Blue
Selected color: Yellow
Selected color: Red
Selected color: Purple
Selected color: Greenこのテクニックは、ランダムなメッセージ表示やランダムイベントの選択など、ゲーム開発やツール作成でよく使われます。
負の数を含む範囲の乱数
-10~10のような対称な範囲

負の値を含めた範囲も、考え方はまったく同じです。
例えば-10~10の乱数を生成するには、次のようにします。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// 先ほどの rand_range_int を再掲
int rand_range_int(int min, int max) {
if (min > max) {
int tmp = min;
min = max;
max = tmp;
}
int range = max - min + 1;
int r = rand() % range;
return min + r;
}
int main(void) {
srand((unsigned int)time(NULL));
for (int i = 0; i < 10; i++) {
int v = rand_range_int(-10, 10);
printf("%d ", v);
}
printf("\n");
return 0;
}(実行例)
-3 7 -10 0 10 -1 5 -8 2 9minとmaxのどちらかが負であっても、差分max - minを使ってrangeを計算しているため、問題なく動作します。
min > max のときの扱い方
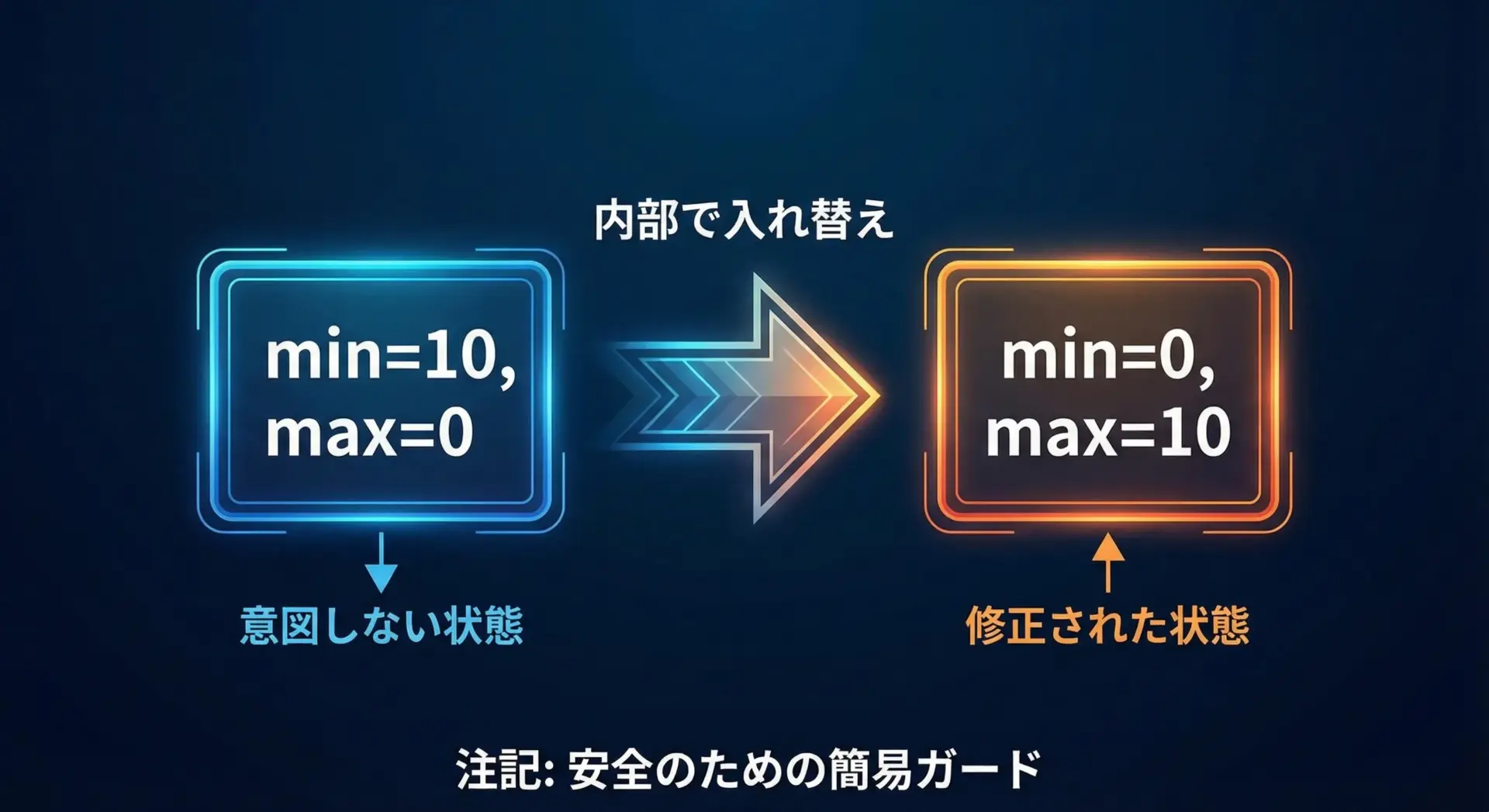
関数に範囲を渡すとき、誤ってminとmaxを逆に指定してしまうことがあります。
サンプルのrand_range_int()では、その場合自動で入れ替える簡易的な防御策を入れました。
厳密な実装では、assert()でチェックしたり、エラーコードを返したりといった処理をすることもあります。
用途に応じて、適切なエラーハンドリングを検討してください。
浮動小数点数の乱数範囲指定
整数だけでなく、小数を含む乱数を扱いたい場面も多くあります。
ここではdoubleを例に、0.0~1.0、任意のmin~maxの生成方法を説明します。
0.0~1.0未満の乱数を生成する

rand()は整数を返しますが、それをdoubleに変換してRAND_MAXで割れば、0.0~1.0の範囲に正規化された乱数が得られます。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double rand_0_1(void) {
// rand() は 0~RAND_MAX の整数
// (double) にキャストしてから割り算をすることで 0.0~1.0 の実数に変換
return (double)rand() / (double)RAND_MAX;
}
int main(void) {
srand((unsigned int)time(NULL));
for (int i = 0; i < 5; i++) {
double x = rand_0_1();
printf("%f\n", x);
}
return 0;
}(実行例)
0.128472
0.932184
0.502931
0.273651
0.761230このrand_0_1()をベースにすれば、任意の実数範囲へ簡単に拡張できます。
任意の実数範囲[min, max)の乱数を生成する
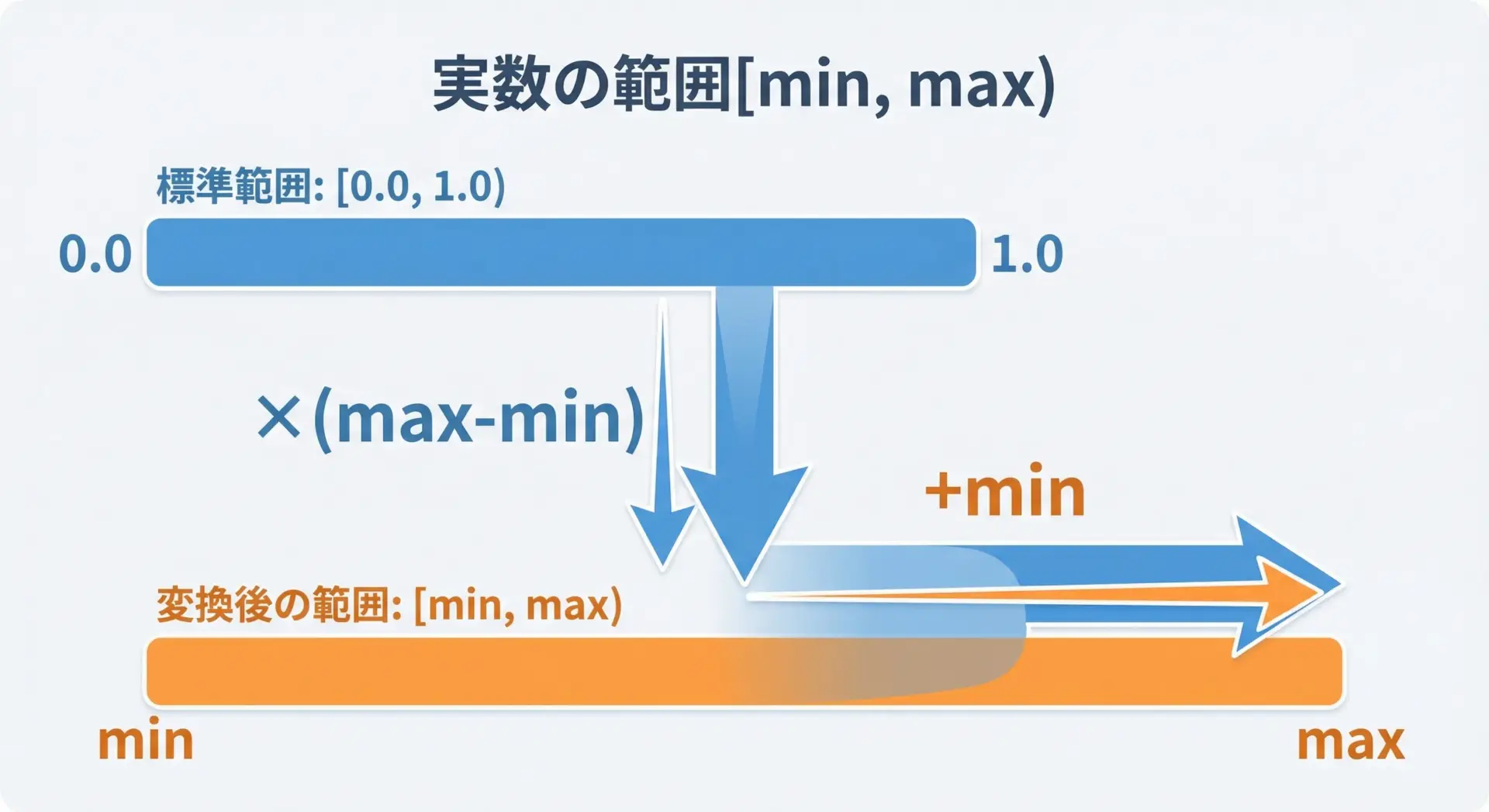
0.0~1.0未満の乱数uがあれば、線形変換によって任意の範囲[min, max)に変換できます。
- 幅をかける:
u * (max - min)は[0.0, max-min) - 下限をシフト:
min + u * (max - min)は[min, max)
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
double rand_0_1(void) {
return (double)rand() / (double)RAND_MAX;
}
// 実数範囲 [min, max) の乱数を返す関数
double rand_range_double(double min, double max) {
if (min > max) {
double tmp = min;
min = max;
max = tmp;
}
double u = rand_0_1(); // 0.0~1.0
return min + u * (max - min); // min~max
}
int main(void) {
srand((unsigned int)time(NULL));
double min = -1.0;
double max = 1.0;
for (int i = 0; i < 5; i++) {
double v = rand_range_double(min, max);
printf("%f\n", v);
}
return 0;
}(実行例)
-0.742119
0.534267
-0.101933
0.984435
-0.317582このように整数版と実数版で共通の「幅を求めてシフトする」考え方を持っておくと、さまざまな乱数の範囲指定を柔軟に設計できます。
簡単な方法の落とし穴: 乱数の偏り問題
rand() % n に潜む偏りの可能性
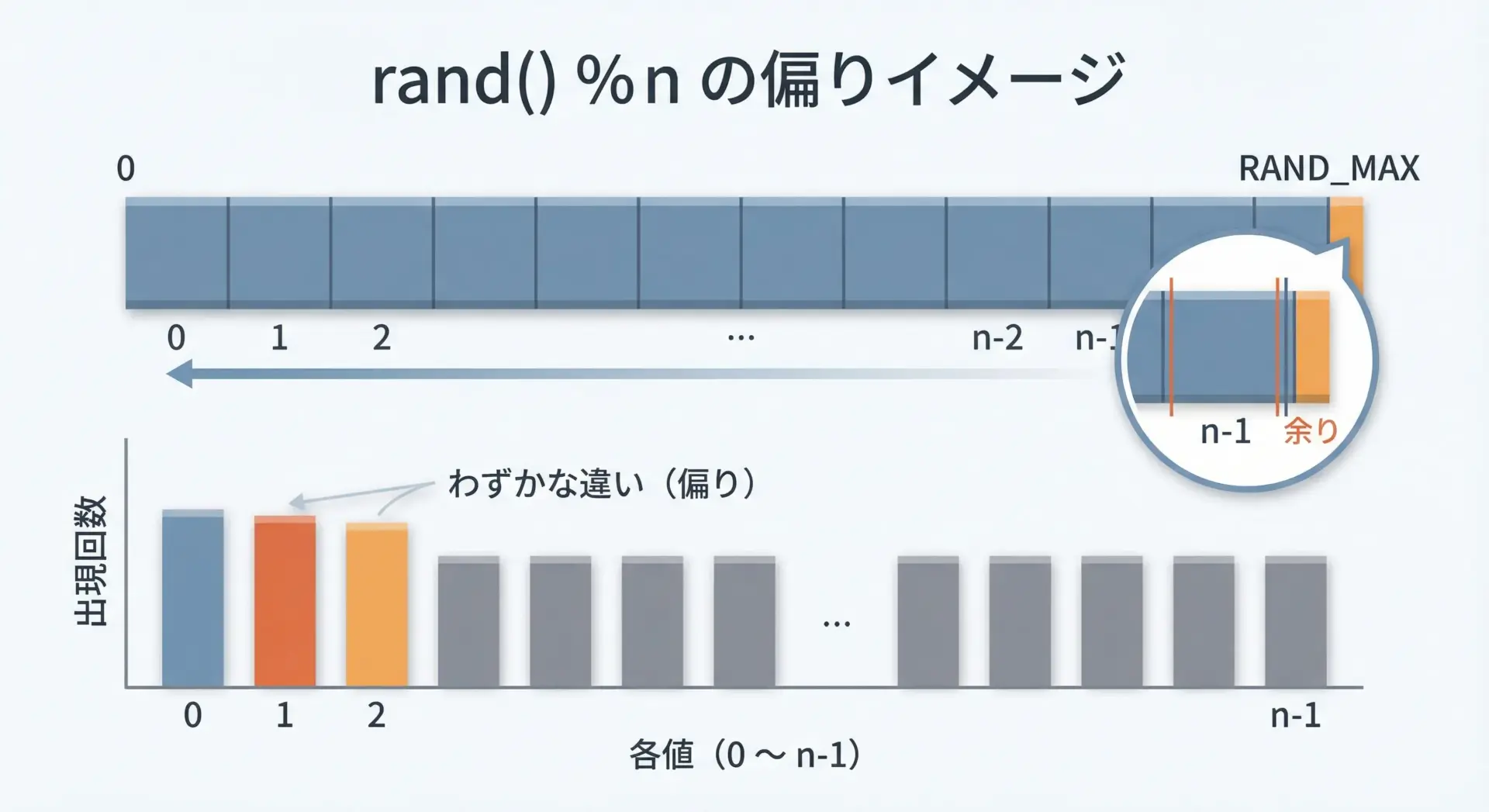
rand() % nは手軽な方法ですが、RAND_MAX + 1 が n で割り切れない場合、値の出現確率にわずかな偏りが生じます。
例として、RAND_MAX+1 = 10、n = 3の極端な仮想例を考えます。
| rand()の値 | rand() % 3 の結果 |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 0 |
| 4 | 1 |
| 5 | 2 |
| 6 | 0 |
| 7 | 1 |
| 8 | 2 |
| 9 | 0 |
この場合、0は4回、1と2は3回ずつ現れます。
つまり、0の方が1や2よりも高確率で出現してしまいます。
実際のRAND_MAXはもっと大きいため偏りはかなり小さくなりますが、統計的な厳密性が必要な用途(暗号、厳密なシミュレーションなど)では問題になる可能性があります。
偏りを抑える「棄却法」による範囲指定
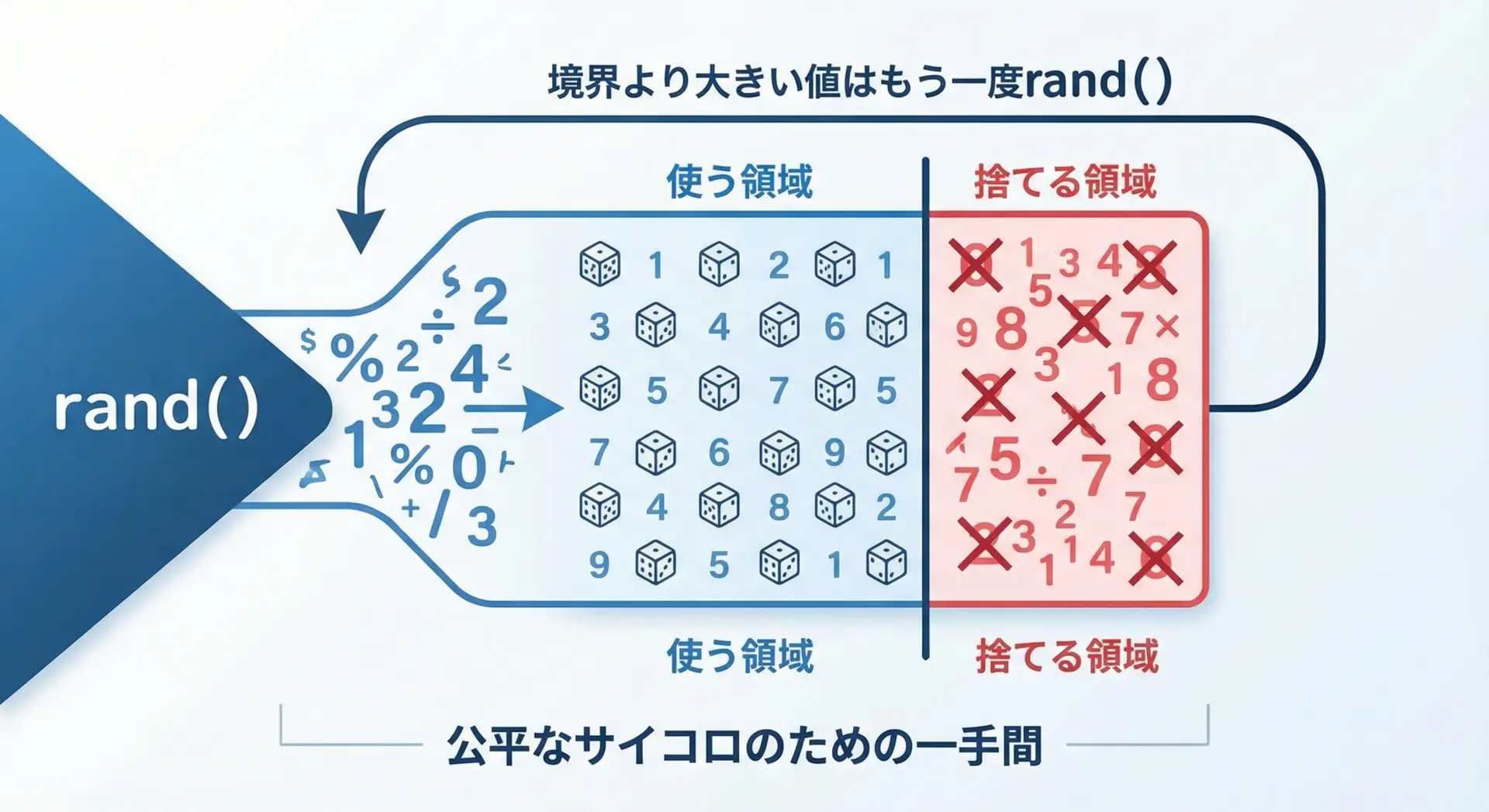
偏りを抑える1つの方法が棄却法(rejection sampling)です。
RAND_MAX+1をnで割ったときのn倍の部分だけを利用し、それ以外の値は「棄却」して、もう一度rand()を呼びます。
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// 偏りを抑えた 0~n-1 の乱数 (棄却法)
int rand_uniform_mod(int n) {
if (n <= 0) {
return 0; // 簡易的な防御(本来はエラー処理した方が良い)
}
// RAND_MAX+1 を n で割ったときの、利用可能な最大値+1
int limit = (RAND_MAX / n) * n; // limit は n の倍数
int r;
do {
r = rand();
} while (r >= limit); // 余った領域に落ちたら引き直し
return r % n; // この時点では偏りがほぼなくなる
}
// min~max の範囲を、上の関数で生成
int rand_range_int_uniform(int min, int max) {
if (min > max) {
int tmp = min;
min = max;
max = tmp;
}
int range = max - min + 1;
int r = rand_uniform_mod(range); // 0~range-1
return min + r;
}
int main(void) {
srand((unsigned int)time(NULL));
// 1~6 の範囲を、偏りを抑えた方法で生成
for (int i = 0; i < 10; i++) {
int dice = rand_range_int_uniform(1, 6);
printf("%d ", dice);
}
printf("\n");
return 0;
}(実行例)
5 3 6 2 1 4 6 2 3 1この実装では、一部のrand()の結果を捨てているため、ループ回数が増える可能性があります。
その代わり、範囲内の各値がより均等な確率で出現するようになります。
「サイコロの公平さ」を重視する用途などで有効です。
より高度な乱数生成手法への道しるべ
C11以降のrand_s()(処理系依存)
一部の処理系(特にWindows環境など)では、rand()よりもよりセキュアな乱数を生成するrand_s()が提供されています。
ただし、これはC標準ではなく処理系固有の拡張であることに注意が必要です。
乱数のセキュリティ性が重要な場面(トークン生成やパスワード生成など)では、標準のrand()は基本的に使うべきではありません。
その場合は、OSやライブラリが提供するセキュア乱数API(例: Linuxの/dev/urandom、WindowsのBCryptGenRandomなど)を利用するのが一般的です。
本記事の範囲指定テクニックは、「0~RAND_MAXの乱数が得られる」という前提に依存しているため、セキュアAPIで得た整数にも同じ変換ロジックを応用できます。
高品質な乱数生成器(Mersenne Twisterなど)
標準のrand()は実装が処理系に依存し、乱数の品質もまちまちです。
そのため、ゲームやシミュレーション、統計計算の分野ではMersenne Twisterやxorshiftなど、より高品質な擬似乱数生成アルゴリズムを利用することが多くなっています。
これらのアルゴリズムは0~ある大きな最大値の整数乱数を返す点ではrand()と同様なので、本記事で説明した「幅を求めてシフトする」範囲指定テクニックはそのまま応用可能です。
よくあるミスと注意点
srand()を何度も呼んでしまう
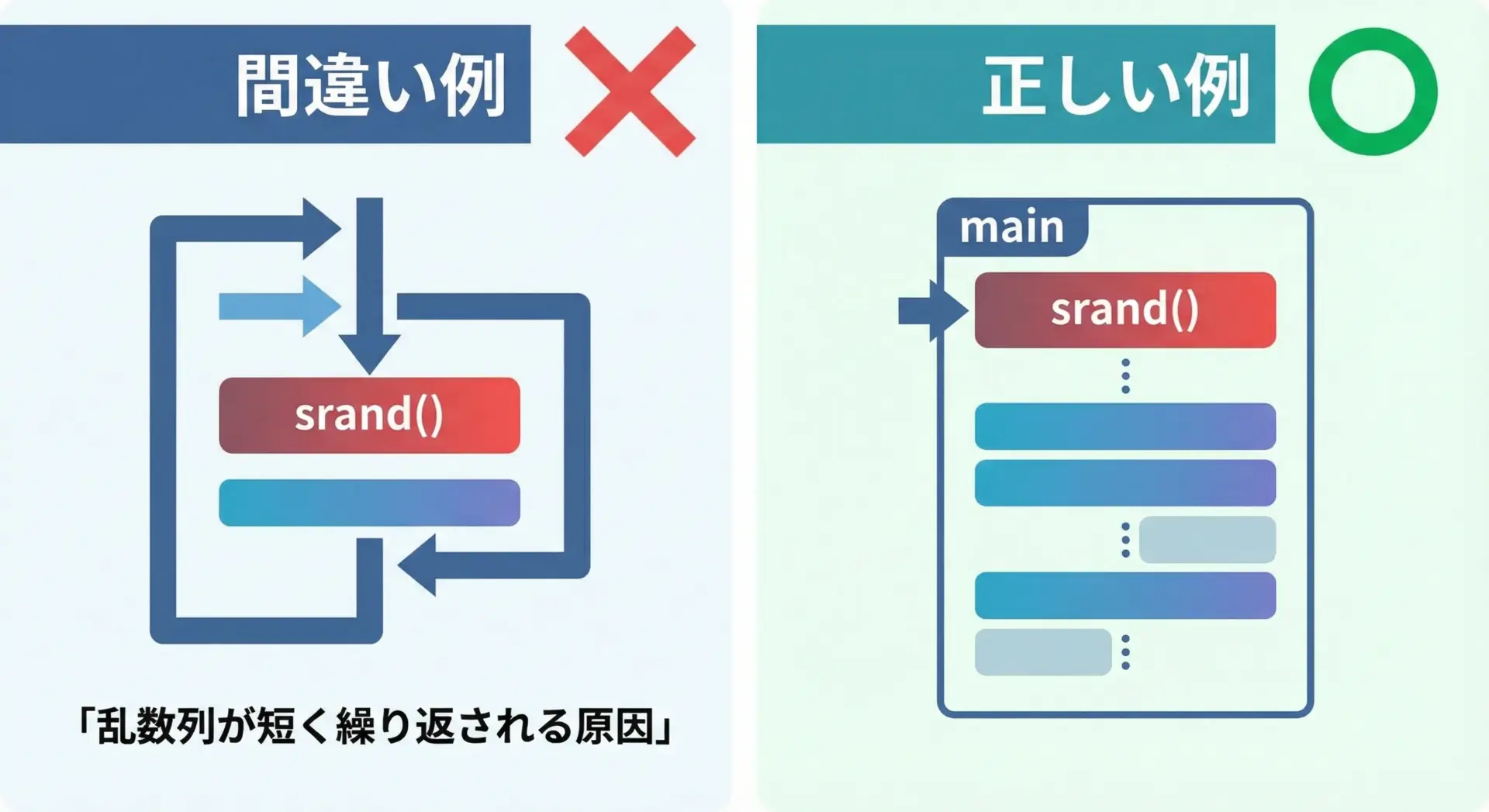
初心者が特にやってしまいがちなミスが、srand()をループの中などで何度も呼び出してしまうことです。
// よくある悪い例(こうしないこと)
for (int i = 0; i < 10; i++) {
srand((unsigned int)time(NULL)); // ループの中で毎回シード設定
int r = rand();
printf("%d\n", r);
}このようにすると、短時間に何度も同じシードが設定され、同じ乱数が繰り返し出るといった問題が起こります。
srand()はプログラムの開始時に1度だけ呼び出し、その後はrand()だけを繰り返し使うようにしてください。
オーバーフローや型変換に注意する
max - min + 1などの計算では、オーバーフローに注意する必要があります。
特にintの範囲いっぱいまで使うような極端な設定を行うと、max - minがintの範囲を超え、未定義動作を引き起こす可能性があります。
実務では、極端な範囲を扱うことはあまり多くありませんが、型の範囲を意識した実装を心がけると安全です。
必要に応じてlongやlong longを使うことも検討してください。
まとめ
本記事では、C言語で乱数を任意の範囲にマッピングするための実践的なテクニックを解説しました。
基本となるrand()とsrand()の使い方から始め、0~n-1、min~maxの整数乱数、負の数を含む範囲、さらに0.0~1.0や任意の実数範囲への拡張方法を紹介しました。
また、rand() % n に潜む偏りの問題と、その対策である棄却法にも触れ、より公平な乱数の作り方の考え方も示しました。
ここで学んだ「幅を求めてシフトする」という共通パターンを押さえておけば、多様な乱数範囲指定を自在に扱えるようになります。
用途に応じて、必要な精度や性能、セキュリティレベルを意識しながら、最適な乱数生成手法を選んでください。

