C言語で整数の割り算をすると、商と余りを別々に計算してしまいがちです。
しかし、標準ライブラリには商と余りを同時に安全に取り出すためのdiv関数が用意されています。
本記事ではC言語のdiv関数の使い方と、商・余りの正しい扱い方を、図解とサンプルコードを交えながらわかりやすく解説します。
C言語における商と余りの基本
Cの整数割り算のルールを押さえる
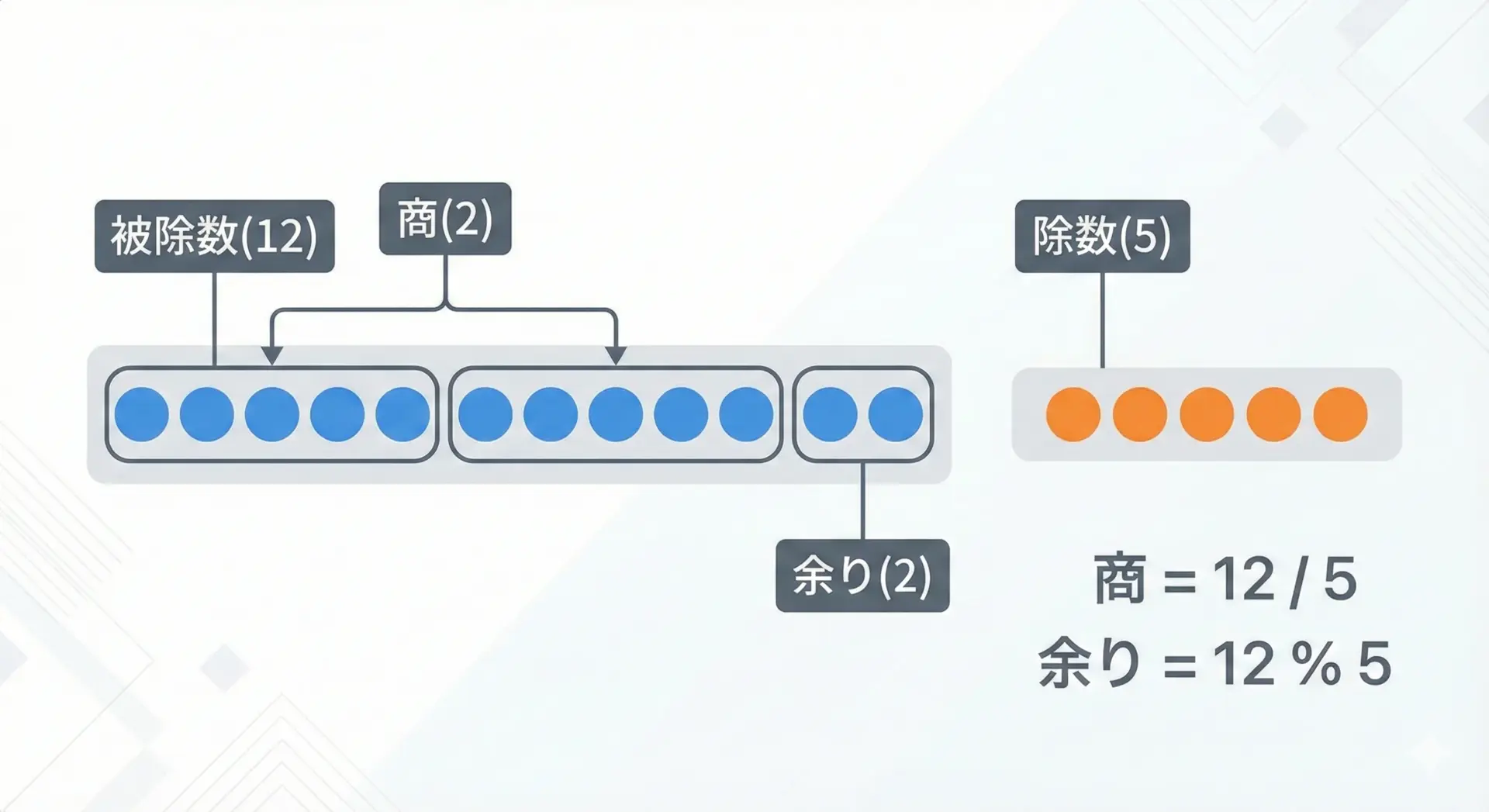
C言語で整数同士の割り算をすると、小数点以下は切り捨てられた商になります。
例えば12 / 5は2.4ではなく2になります。
そして余りは12 % 5と書くことで2を得られます。
このとき、割り算は「商」と「余り」の2つの顔を持つことをイメージしておくと理解しやすくなります。
1つの被除数に対して、除数が何回入るかが商、入りきらずに残った分が余りです。
商と余りの関係式

整数の割り算では、次のような等式が必ず成り立ちます。
a = b × 商 + 余り
ここで、aは被除数、bは除数です。
例えばa = 12、b = 5とすると、商は2、余りは2ですから、
12 = 5 × 2 + 2
となり、関係式がきちんと成り立っていることがわかります。
div関数とは何か
div関数の役割と特徴
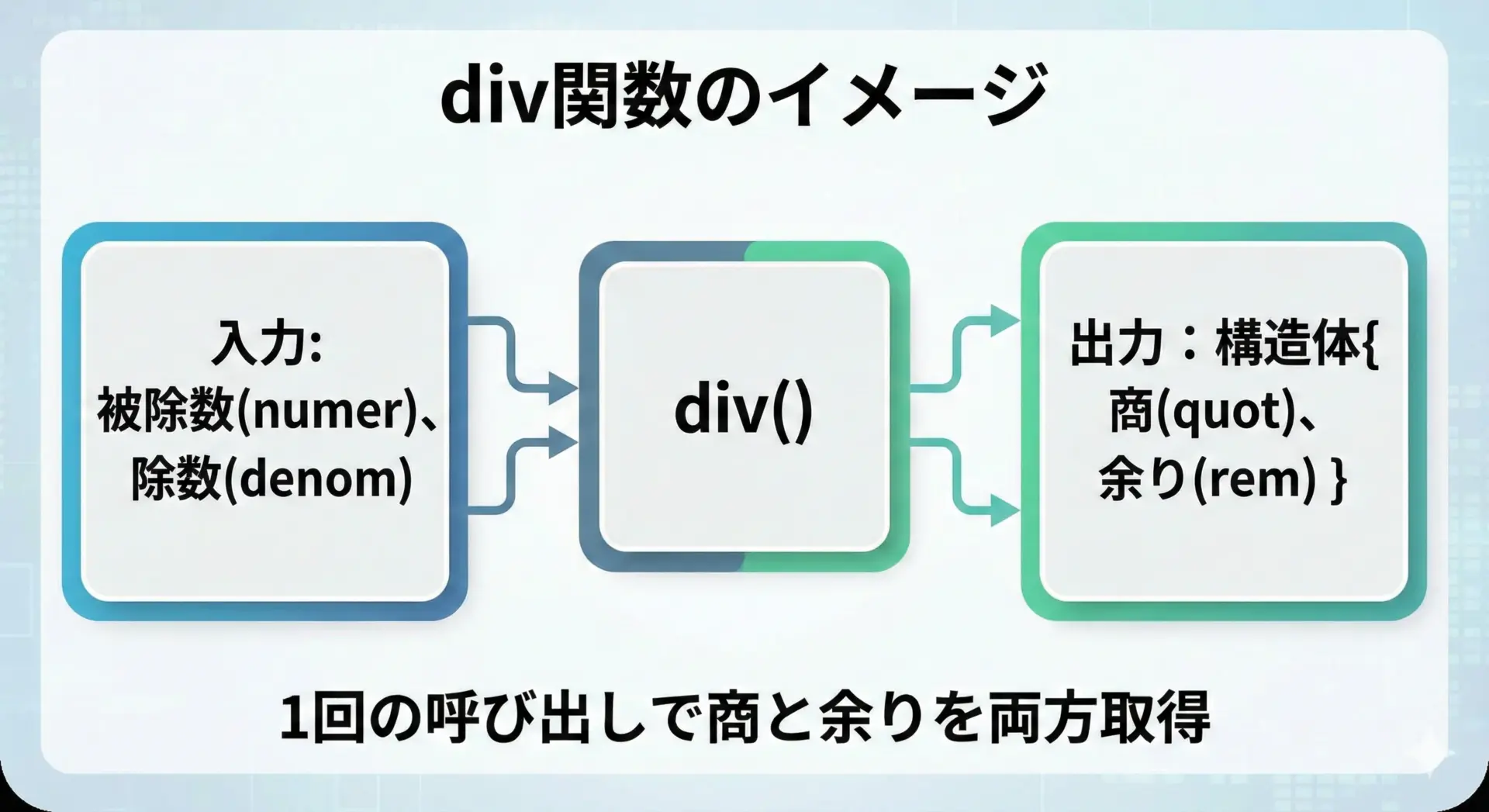
C言語の標準ライブラリには、整数の商と余りを同時に計算するためのdiv関数が用意されています。
通常、商は/演算子、余りは%演算子で個別に求めますが、divを使うと1回の関数呼び出しでまとめて取得できます。
特徴を文章で整理すると、次のようになります。
商と余りをセットにした構造体を返す特殊な関数であり、しかも標準ライブラリで決められた型div_tを返します。
div関数の宣言とヘッダ

div関数を使うには、#include <stdlib.h>が必要です。
宣言は標準では次のようになっています。
/* stdlib.h(イメージ) */
typedef struct {
int quot; /* 商(quotient) */
int rem; /* 余り(remainder) */
} div_t;
/* div関数の宣言 */
div_t div(int numer, int denom);つまり、divは戻り値としてdiv_tという構造体型を返し、その中にquot(商)とrem(余り)が格納されます。
div_t構造体の中身を理解する
div_tの構造とは
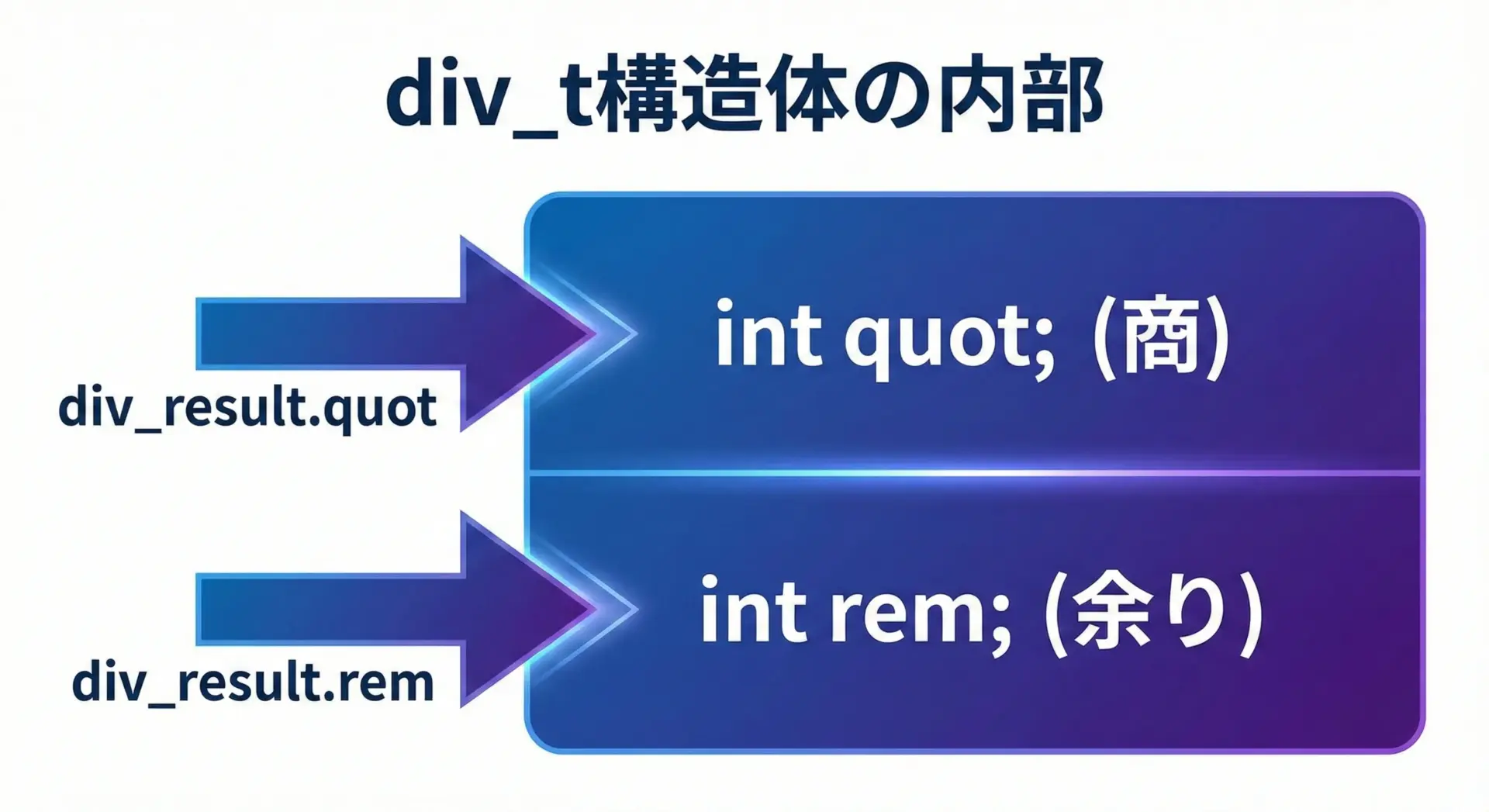
div_tは商と余りをまとめて保持するための構造体型です。
標準では次のように定義されています。
typedef struct {
int quot; /* 商(quotient) */
int rem; /* 余り(remainder) */
} div_t;ここで重要なのは、戻り値が構造体だからこそ商と余りを1セットとして扱えるという点です。
計算結果の整合性を保つ意味でも有効です。
メンバへのアクセス方法
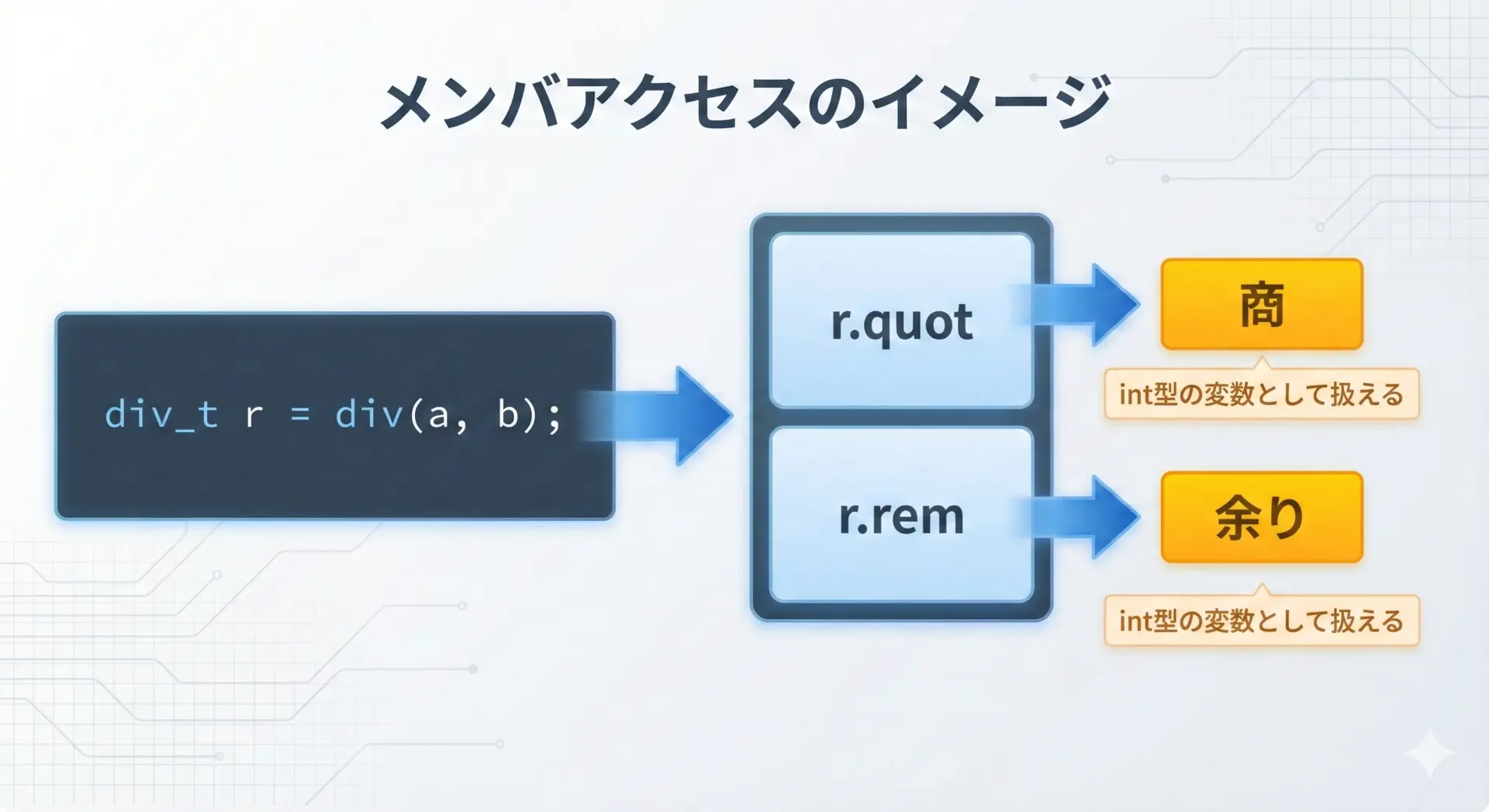
div_t型の変数から商と余りを取り出すには、構造体のメンバアクセス演算子.を使います。
div_t result = div(12, 5);
int q = result.quot; /* 商: 2 */
int r = result.rem; /* 余り: 2 */このようにresult.quotやresult.remは、普通のint型変数のように扱えます。
基本的なdiv関数の使い方
最小のサンプルコードで流れを確認する
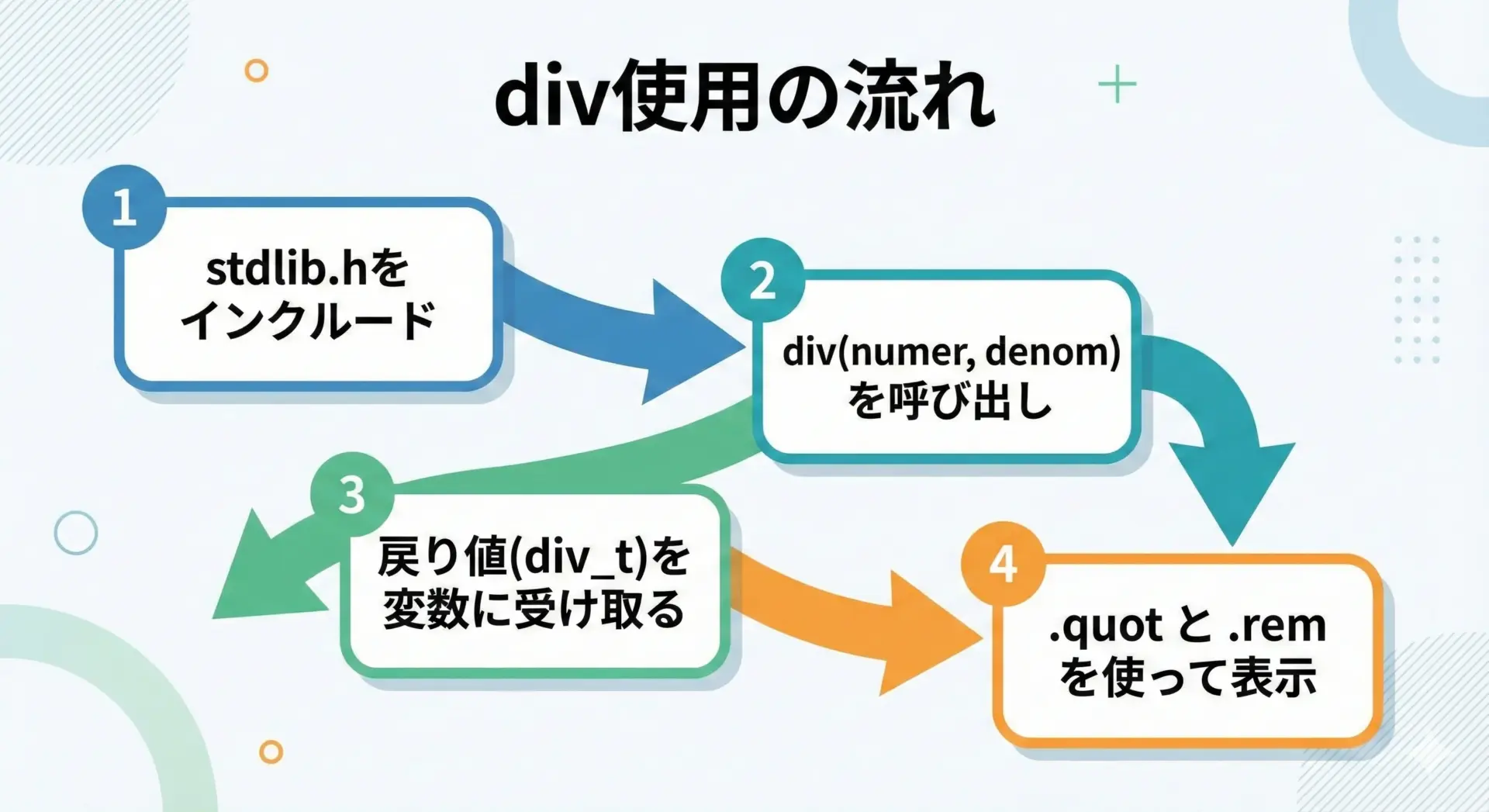
まずはdiv関数の基本的な使い方を、シンプルなプログラムで確認してみます。
#include <stdio.h>
#include <stdlib.h> /* div, div_t を使うために必要 */
/* div関数の基本的な使い方のサンプル */
int main(void) {
int a = 12; /* 被除数(numer) */
int b = 5; /* 除数(denom) */
/* divを呼び出して商と余りを同時に取得 */
div_t result = div(a, b);
/* 結果を表示 */
printf("a = %d, b = %d\n", a, b);
printf("商(quot) = %d\n", result.quot);
printf("余り(rem) = %d\n", result.rem);
return 0;
}a = 12, b = 5
商(quot) = 2
余り(rem) = 2このプログラムでは、1回のdiv呼び出しで商と余りを同時に取得し、それぞれを表示しています。
/ と % の組み合わせとの比較
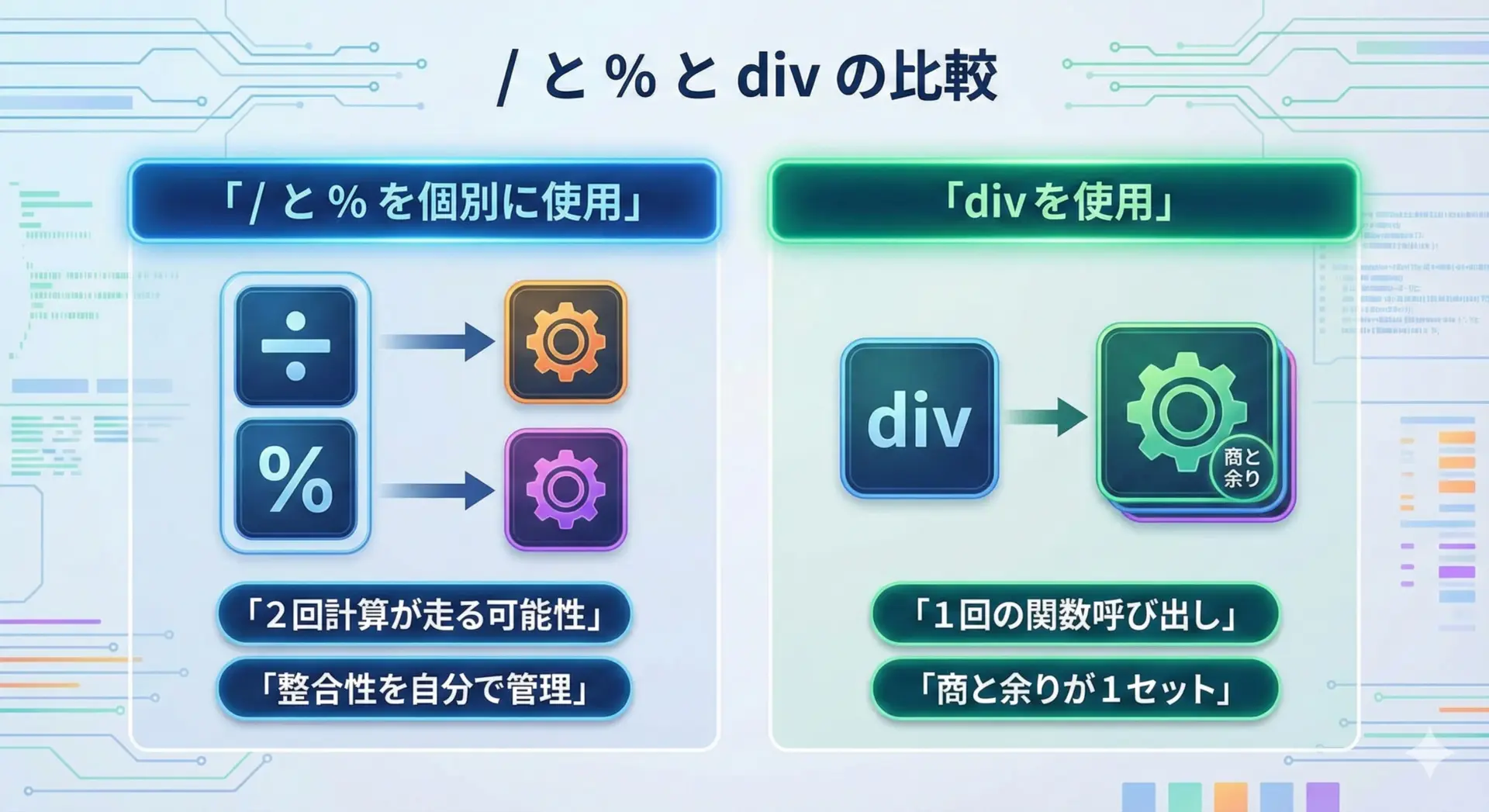
/と%を使っても同じ結果を得られますが、divには次のような利点があります。
- 計算が1回の関数呼び出しにまとまるため、コードの見通しが良くなること。
- 商と余りを1つの構造体として扱えるので、セットで渡したり戻したりしやすいこと。
一方で、パフォーマンス面では処理系によって挙動が異なり、コンパイラが最適化してくれる場合も多いため、速度を厳密に比較するというよりは、「コードの意図が明確になる」というメリットに注目すると良いです。
long型やlong long型用のldiv・lldiv
ldivとlldivの概要
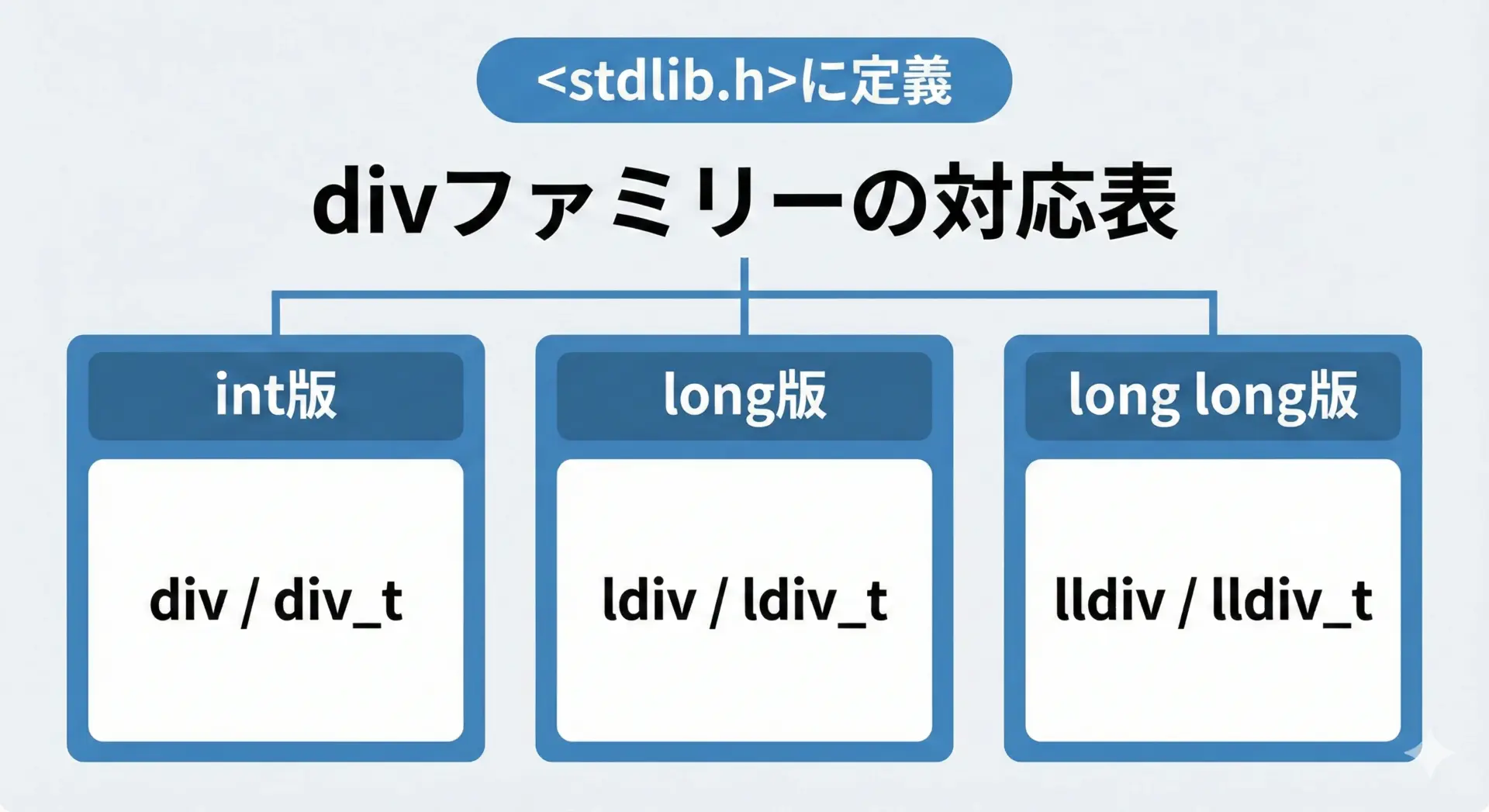
より大きな整数型に対しても、商と余りを同時に求めるための関数が用意されています。
ldiv:long型用。戻り値の型はldiv_tlldiv:long long型用。戻り値の型はlldiv_t
宣言イメージは次のようになっています。
/* long用 */
typedef struct {
long quot; /* 商 */
long rem; /* 余り */
} ldiv_t;
ldiv_t ldiv(long numer, long denom);
/* long long用 */
typedef struct {
long long quot; /* 商 */
long long rem; /* 余り */
} lldiv_t;
lldiv_t lldiv(long long numer, long long denom);いずれも<stdlib.h>に宣言されています。
ldiv / lldiv のサンプル
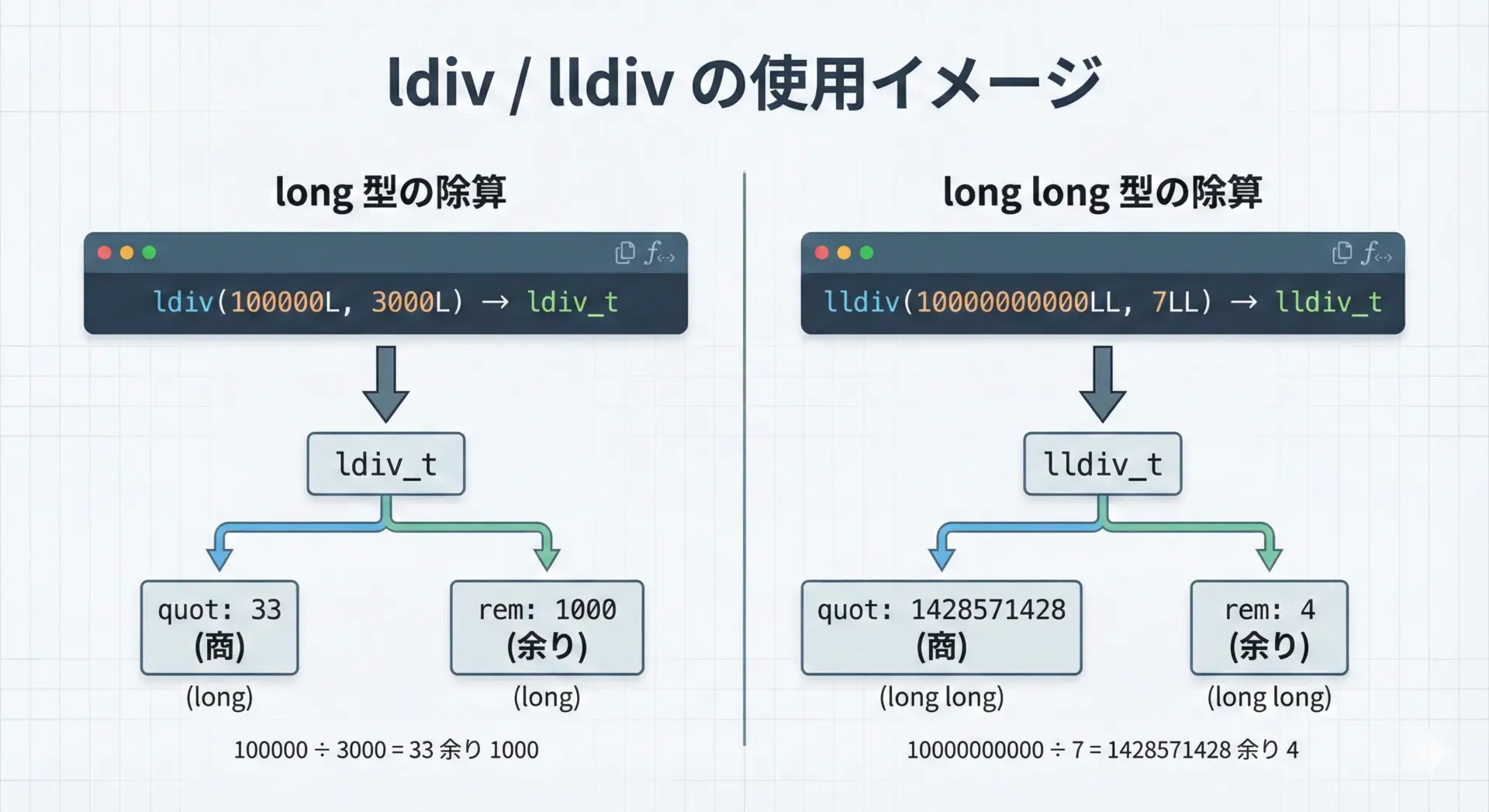
大きな整数を扱うときの例を示します。
#include <stdio.h>
#include <stdlib.h> /* ldiv, ldiv_t, lldiv, lldiv_t */
int main(void) {
long la = 100000L;
long lb = 3000L;
/* long版: ldiv */
ldiv_t lres = ldiv(la, lb);
long long lla = 10000000000LL; /* 1e10 */
long long llb = 7LL;
/* long long版: lldiv */
lldiv_t llres = lldiv(lla, llb);
printf("[ldivの結果]\n");
printf("la = %ld, lb = %ld\n", la, lb);
printf("商(quot) = %ld\n", lres.quot);
printf("余り(rem) = %ld\n", lres.rem);
printf("\n[lldivの結果]\n");
printf("lla = %lld, llb = %lld\n", lla, llb);
printf("商(quot) = %lld\n", llres.quot);
printf("余り(rem) = %lld\n", llres.rem);
return 0;
}[ldivの結果]
la = 100000, lb = 3000
商(quot) = 33
余り(rem) = 1000
[lldivの結果]
lla = 10000000000, llb = 7
商(quot) = 1428571428
余り(rem) = 4扱う整数のサイズに応じてdiv / ldiv / lldivを選ぶことで、桁あふれを防ぎつつ、安全に商と余りを取り扱えます。
div関数を自分で作る必要はあるか
標準ライブラリを使うべき理由
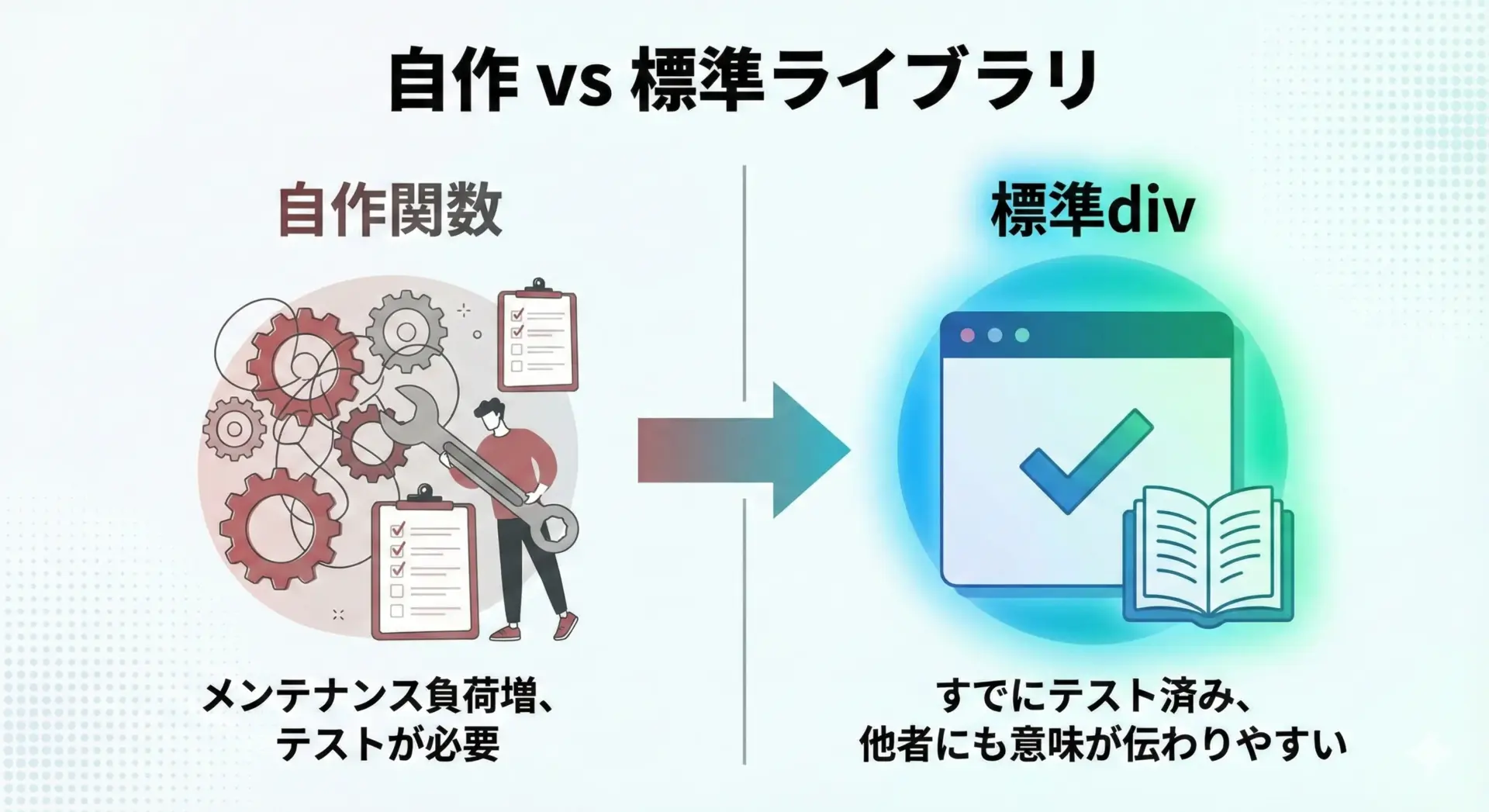
商と余りを同時に返す関数は、自分で実装することもできます。
しかし、C言語ではすでにdivという標準関数が用意されています。
そのため、通常は自作するより標準ライブラリを利用した方が安全です。
標準関数を使うべき主な理由は次のとおりです。
- すでに多くの環境でテストされており、挙動が安定していること。
- 他のプログラマにとって意味がすぐ伝わること。
- 将来のメンテナンスや移植性の面で有利であること。
それでも自作する場合の注意点

学習目的などであえて自分で実装する場合には、ゼロ除算と型の範囲に注意する必要があります。
また、a = b × 商 + 余りという関係がズレないようにテストすることも重要です。
商と余りを同時に扱うことのメリット
一貫性のある計算結果を得やすい
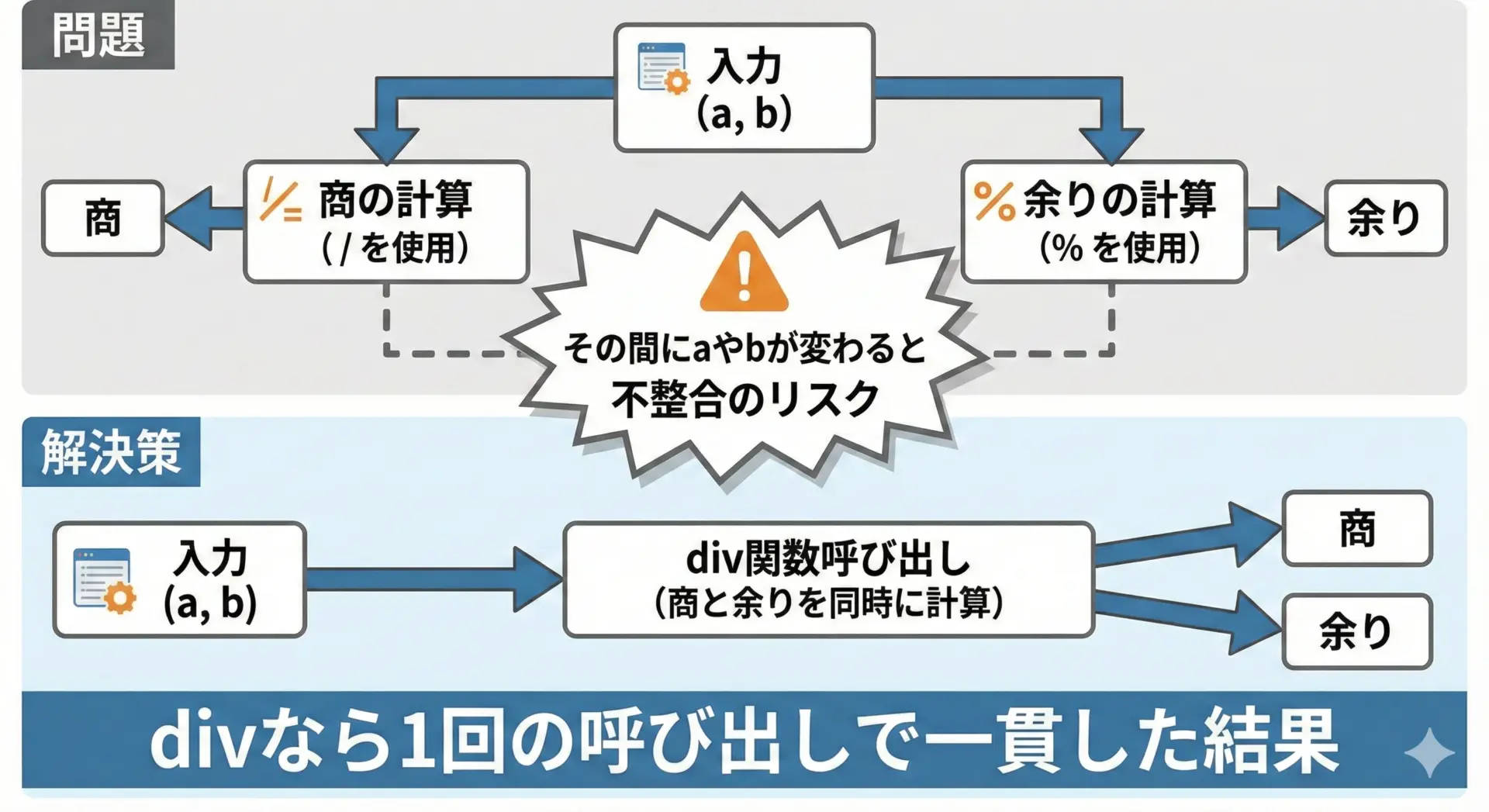
/と%を別々に呼び出すと、極端な状況では途中で値が書き換えられ、不整合な結果になるリスクがあります。
通常の単純なプログラムではあまり問題になりませんが、マルチスレッドや割り込みを扱う環境では注意が必要です。
divを使うと、特定のペア<numer, denom>に対する商と余りが一度に決まるため、このようなリスクを減らすことができます。
まとめて返したいときに便利
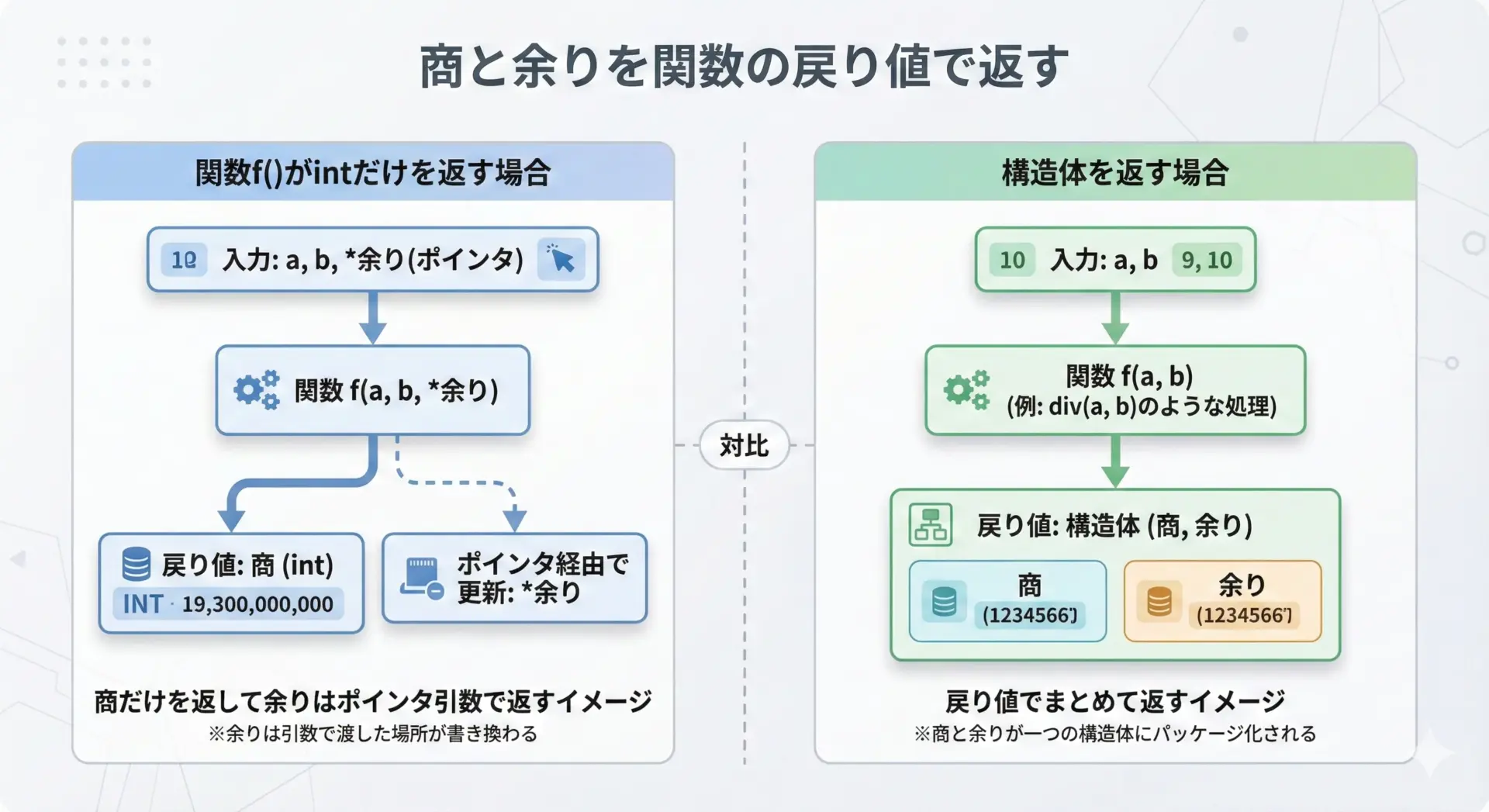
商と余りの両方が必要な処理では、構造体を戻り値にするとコードがシンプルになります。
divやldivはまさにこのパターンで、戻り値として「商+余りのセット」を返します。
これは、別の自作関数の中でdivを呼び出し、そのまま戻り値として受け渡すようなケースでも役立ちます。
実践的なサンプル1: / と % と divの結果比較
比較用のプログラムを作る

実際に/、%、divで得られる結果を比較してみます。
#include <stdio.h>
#include <stdlib.h>
/* /, %, div の結果を比較するサンプル */
int main(void) {
int a = 17;
int b = 5;
/* / と % を個別に計算 */
int q_op = a / b; /* 商 */
int r_op = a % b; /* 余り */
/* div 関数でまとめて計算 */
div_t d = div(a, b);
printf("a = %d, b = %d\n\n", a, b);
printf("[/ と %% 演算子による結果]\n");
printf("商 = %d, 余り = %d\n\n", q_op, r_op);
printf("[div 関数による結果]\n");
printf("商(quot) = %d, 余り(rem) = %d\n\n", d.quot, d.rem);
/* 関係式 a = b * 商 + 余り を確認 */
printf("確認: a == b * 商 + 余り ?\n");
printf("%d == %d * %d + %d → %s\n",
a, b, d.quot, d.rem,
(a == b * d.quot + d.rem) ? "OK" : "NG");
return 0;
}実行結果の例を示します。
a = 17, b = 5
[/ と % 演算子による結果]
商 = 3, 余り = 2
[div 関数による結果]
商(quot) = 3, 余り(rem) = 2
確認: a == b * 商 + 余り ?
17 == 5 * 3 + 2 → OKこのように、/と%で求めた結果とdivの結果が一致していることがわかります。
実践的なサンプル2: 負の数とdivの挙動に注意
C99以降の除算ルールを知る
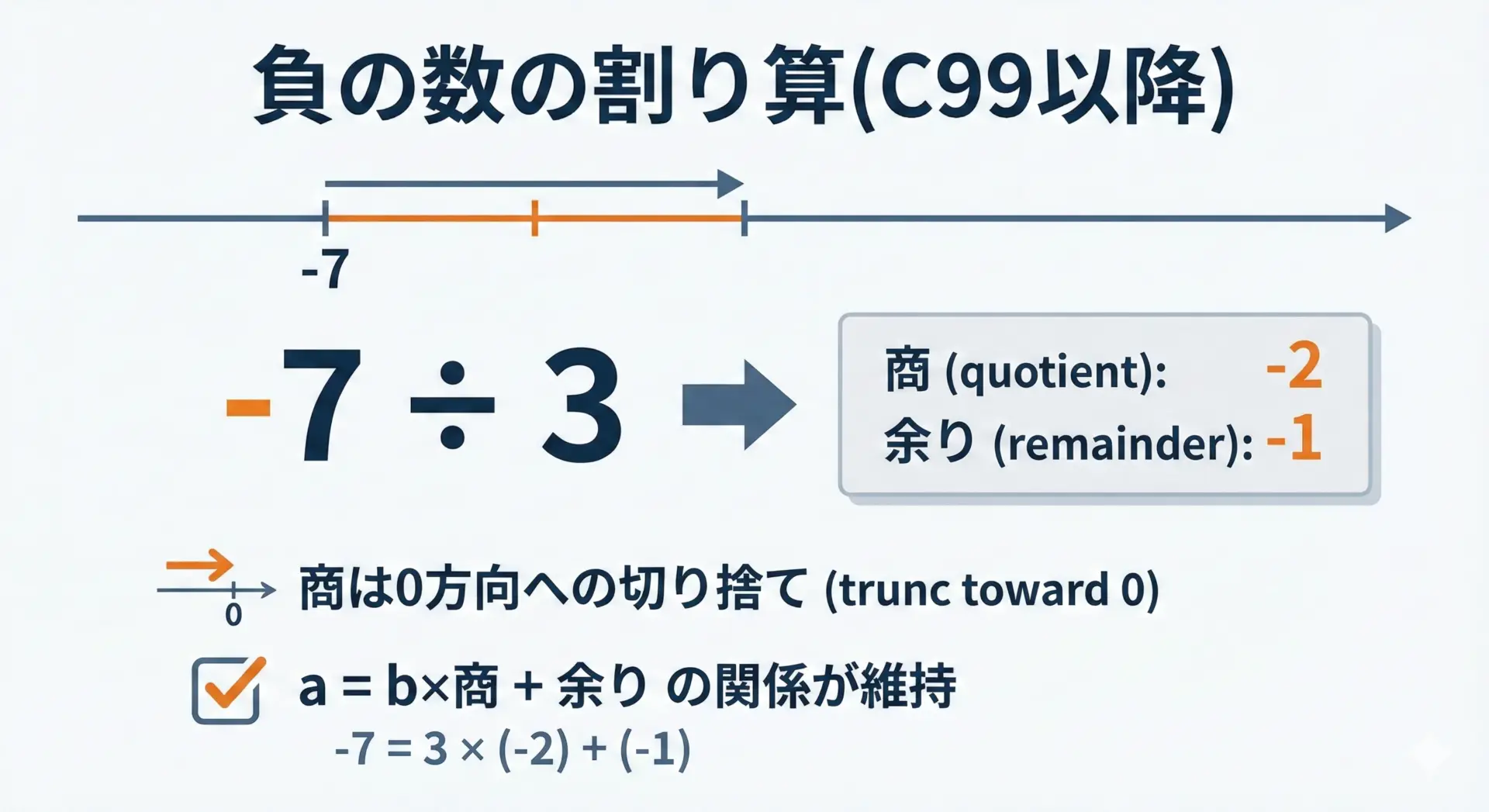
C99以降のC言語では、整数除算は0方向への切り捨てと定義されています。
つまり-7 / 3は-2になり、余りは-1です。
このときa = b × 商 + 余りを確認すると、
-7 = 3 × (-2) + (-1)
となり、きちんと関係式が成り立ちます。
divもこのルールに従うため、負の数が出てくるケースでも一貫した結果が得られます。
負の値でdivを試すサンプル
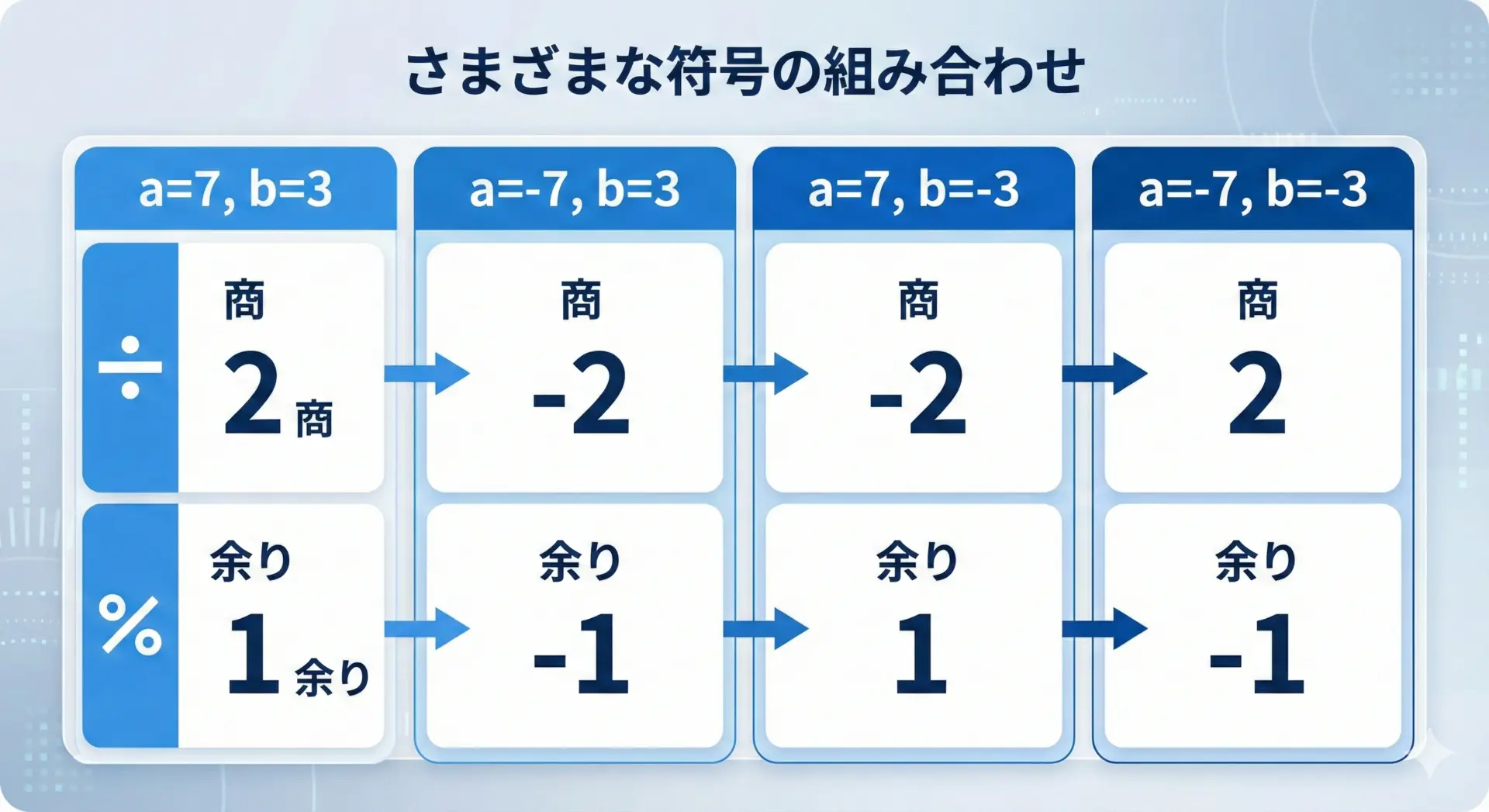
負の数を混ぜたケースでdivの挙動を確認してみます。
#include <stdio.h>
#include <stdlib.h>
/* 負の数を含む div の挙動を確認するサンプル */
void test_div(int a, int b) {
div_t r = div(a, b);
printf("a = %d, b = %d\n", a, b);
printf(" 商(quot) = %d\n", r.quot);
printf(" 余り(rem) = %d\n", r.rem);
printf(" 確認: %d == %d * %d + %d → %s\n\n",
a, b, r.quot, r.rem,
(a == b * r.quot + r.rem) ? "OK" : "NG");
}
int main(void) {
test_div(7, 3);
test_div(-7, 3);
test_div(7, -3);
test_div(-7, -3);
return 0;
}a = 7, b = 3
商(quot) = 2
余り(rem) = 1
確認: 7 == 3 * 2 + 1 → OK
a = -7, b = 3
商(quot) = -2
余り(rem) = -1
確認: -7 == 3 * -2 + -1 → OK
a = 7, b = -3
商(quot) = -2
余り(rem) = 1
確認: 7 == -3 * -2 + 1 → OK
a = -7, b = -3
商(quot) = 2
余り(rem) = -1
確認: -7 == -3 * 2 + -1 → OKすべてのパターンでa = b × 商 + 余りが成立していることが確認できます。
負の数が絡むときは、商や余りの符号にも注意が必要です。
実践的なサンプル3: ゼロ除算を避ける安全な使い方
denomが0の場合は未定義動作

divに限らず、C言語では0で割ることは未定義動作(UB)です。
div(a, 0)やa / 0は、実行時エラーやクラッシュ、予期しない挙動の原因となります。
そのため、除数が0でないことを事前にチェックするのが安全な書き方です。
安全なラッパー関数の例
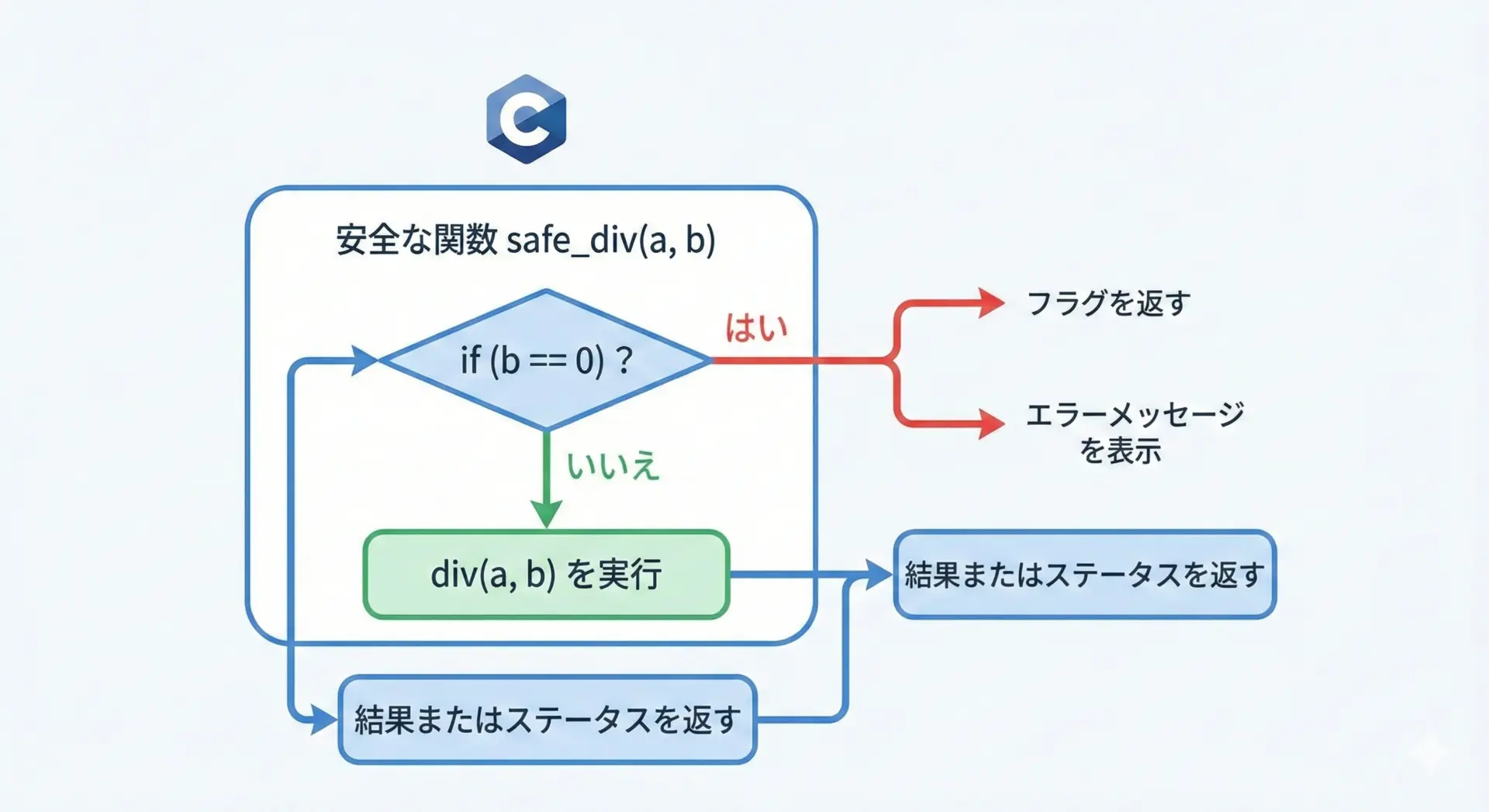
ゼロ除算を避けるための簡単なラッパー関数を作ってみます。
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
/* 商と余りと、成功/失敗フラグを含む構造体 */
typedef struct {
div_t value; /* div の結果(商と余り) */
bool ok; /* 計算が成功したかどうか */
} safe_div_result;
/* ゼロ除算チェック付きの安全なdivラッパー関数 */
safe_div_result safe_div(int a, int b) {
safe_div_result res;
if (b == 0) {
/* 0で割ることはできないので、フラグだけfalseにする */
res.ok = false;
} else {
res.value = div(a, b); /* 安全に計算 */
res.ok = true;
}
return res;
}
int main(void) {
int a = 10;
int b1 = 2;
int b2 = 0;
safe_div_result r1 = safe_div(a, b1);
safe_div_result r2 = safe_div(a, b2);
if (r1.ok) {
printf("a = %d, b1 = %d のとき: 商 = %d, 余り = %d\n",
a, b1, r1.value.quot, r1.value.rem);
} else {
printf("a = %d, b1 = %d のとき: 計算失敗\n", a, b1);
}
if (r2.ok) {
printf("a = %d, b2 = %d のとき: 商 = %d, 余り = %d\n",
a, b2, r2.value.quot, r2.value.rem);
} else {
printf("a = %d, b2 = %d のとき: ゼロ除算のため計算できません\n", a, b2);
}
return 0;
}実行結果の一例は次のとおりです。
a = 10, b1 = 2 のとき: 商 = 5, 余り = 0
a = 10, b2 = 0 のとき: ゼロ除算のため計算できませんこのように、ゼロ除算を検出して安全に扱えるような仕組みを自作することも可能です。
divを使うべきケースと、使わなくてもよいケース
divを使うと読みやすくなるケース
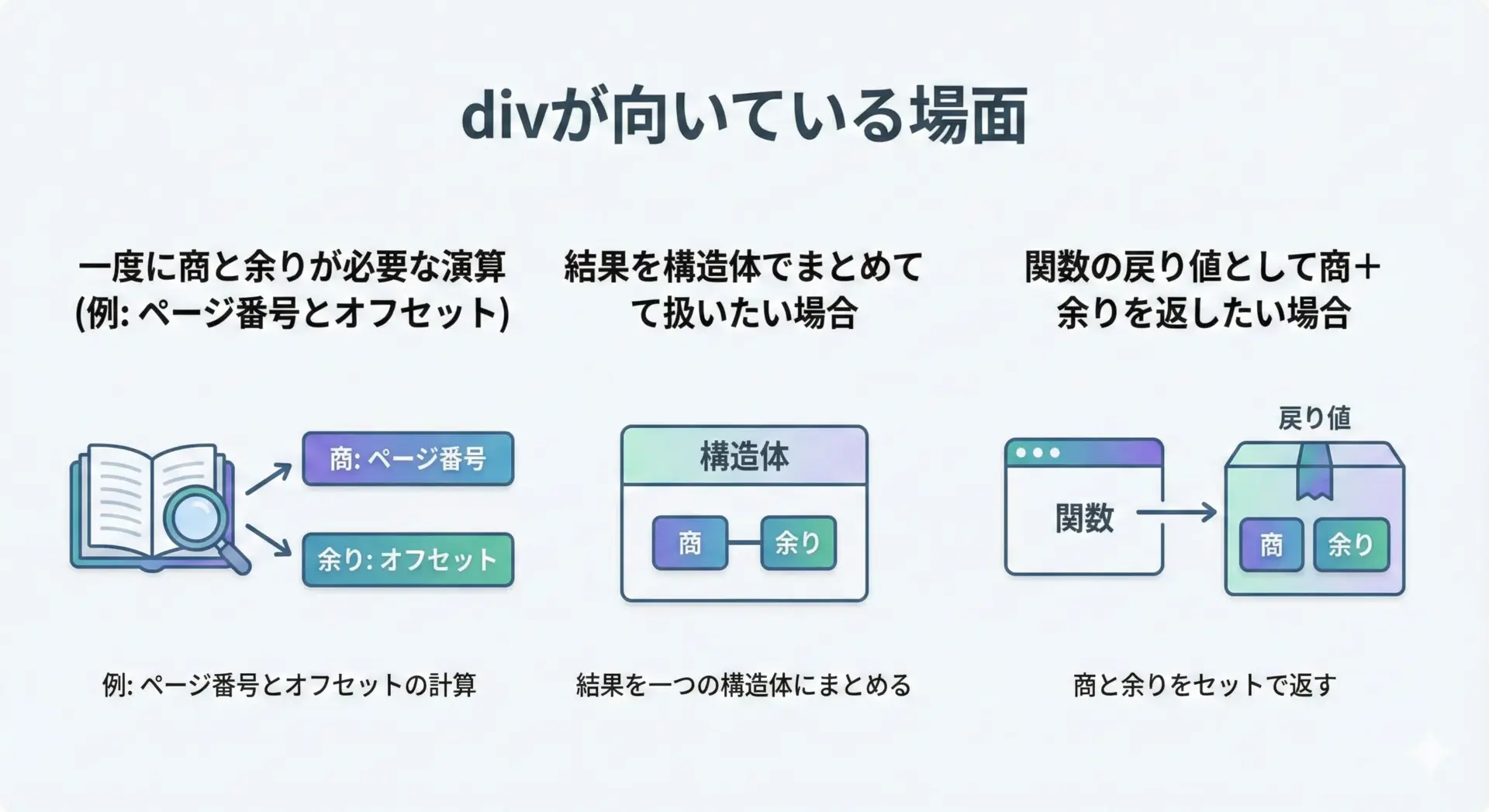
divを使うと、特に次のような場面でコードの意図が明確になり、読みやすくなります。
商と余りが常にセットで必要な場合には、divを使うことで「セットで扱っている」ことが明示的に伝わるため、コードの可読性が向上します。
/ と % で十分なケース

一方で、用途が非常に単純な場合には/と%を直接使った方が読みやすいこともあります。
例えば以下のような場合です。
if (x % 2 == 0)のような偶数判定- 配列のインデックスを少し調整するために
i / 2だけ使う場合
このように、用途に応じてdivと演算子を使い分けるのが実務的です。
まとめ
C言語では、整数の商と余りを同時に取り扱うための標準関数としてdivが用意されています。
divはdiv_tという構造体を返し、そのquotメンバに商、remメンバに余りが格納されます。
より大きな整数型にはldivやlldivが対応しており、桁数に応じて使い分けることができます。
/と%を個別に使う方法もありますが、商と余りをセットで扱いたい場面ではdiv系関数が読みやすく安全です。
ゼロ除算や負の数の扱いには注意しつつ、用途に応じてdivと演算子を使い分けることで、より分かりやすく堅牢なCプログラムを書くことができます。

