C言語で浮動小数点の剰余を求めるとき、整数演算の%演算子はそのままでは使えません。
そこで登場するのがfmod関数です。
本記事では、fmodの基本的な使い方から、負の数やゼロを含む場合の挙動、実践的な注意点までを、図解とサンプルコードを交えながら丁寧に解説します。
C言語における剰余演算の基本
整数の剰余と浮動小数点の剰余の違い
整数に対する%演算子
C言語では、整数型に対して%演算子を使うことで剰余を求めることができます。
例えば、7 % 3は1になります。
しかし、この%演算子は整数専用です。
浮動小数点数(floatやdouble)に対して使うことはできません。
浮動小数点でそのまま%cst-code>%が使えない理由
浮動小数点数は、小数部を持つ実数を近似的に表現するための形式です。
そのため、整数演算を前提とした%演算子とは性質が異なり、コンパイラは次のようなエラーを出します。
double a = 5.5;
double b = 2.0;
// コンパイルエラーになる例
double r = a % b; // エラー: invalid operands to binary %浮動小数点に対しても剰余を求めたい場面は多いため、そのために標準ライブラリが用意しているのがfmod関数です。
fmod関数とは
fmodの基本仕様とヘッダファイル
fmodのプロトタイプ
fmodは、C標準ライブラリのmath.hに定義されている、浮動小数点用の剰余関数です。
#include <math.h>
double fmod(double x, double y);
float fmodf(float x, float y);
long double fmodl(long double x, long double y);最もよく使われるのはdouble版のfmodです。
fmodfはfloat用、fmodlはlong double用です。
fmodが返す値の意味
fmod(x, y)は「xをyで割った余り」を返しますが、整数の%と同じに見えて、少し細かな仕様があります。
- 値の範囲として、絶対値は
|y|より小さい - 戻り値の符号はxと同じになります
式で書くと、次の性質を満たします。
fmod(x, y) = x - n * y(nは0に最も近い整数)fabs(fmod(x, y)) < fabs(y)fmod(x, y)の符号はxと同じ、またはゼロ
fmodの動作イメージを図で理解する
商と剰余の関係を視覚的にとらえる
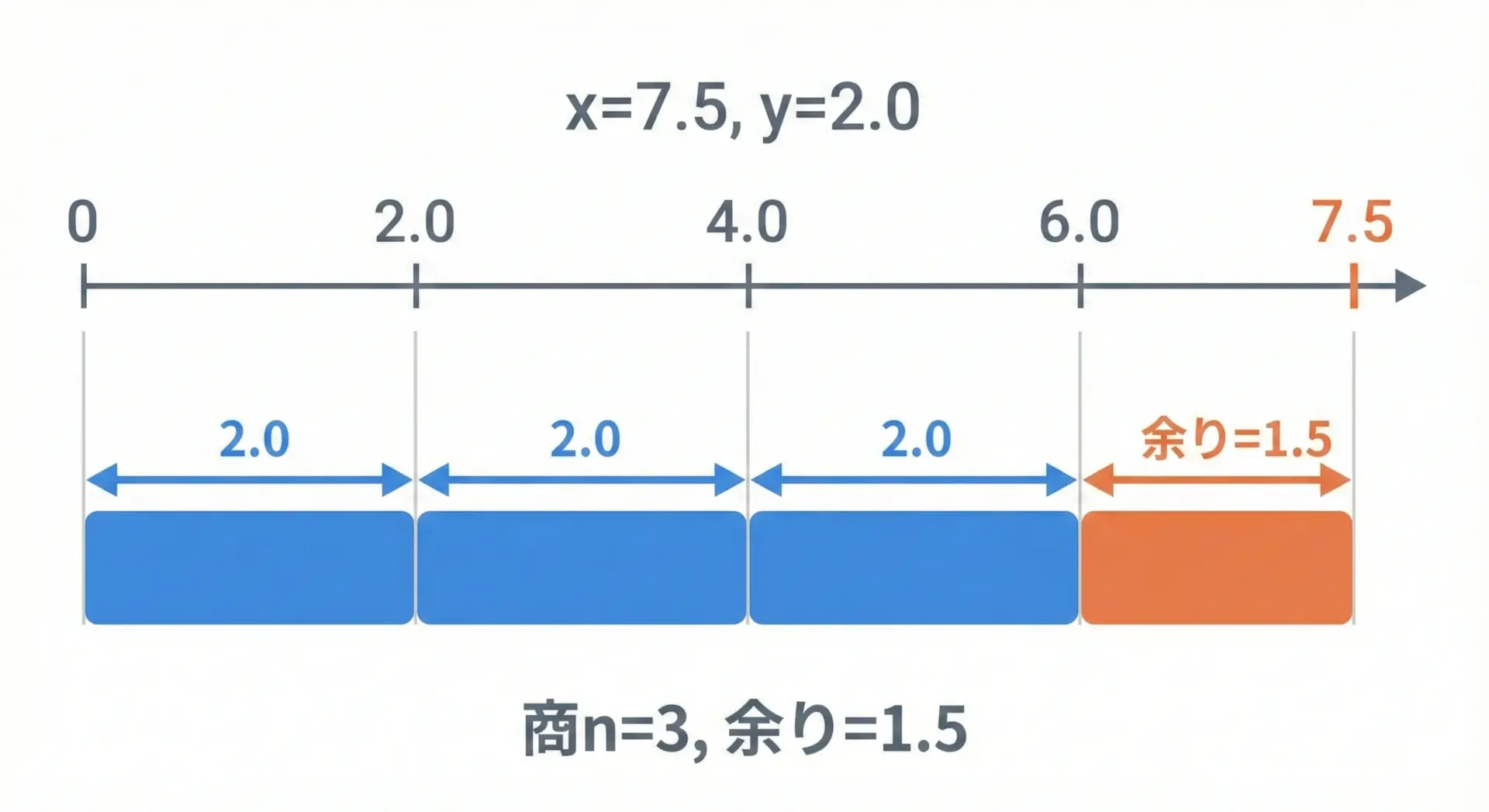
このように、fmodはxをyで割ったときに「入りきらなかった端数部分」を返す関数です。
整数の%と概念的には同じですが、実数上の連続的な位置を扱う点に違いがあります。
基本的な使い方(実例付き)
最もシンプルな使用例
小数の剰余を求めるサンプルコード
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 7.5;
double y = 2.0;
// fmodを使って浮動小数点の剰余を求める
double r = fmod(x, y);
printf("x = %.2f, y = %.2f\n", x, y);
printf("fmod(x, y) = %.2f\n", r); // 期待値は 1.50
return 0;
}x = 7.50, y = 2.00
fmod(x, y) = 1.50ここでは7.5 / 2.0の剰余として1.5が返っていることが確認できます。
整数との比較で理解を深める
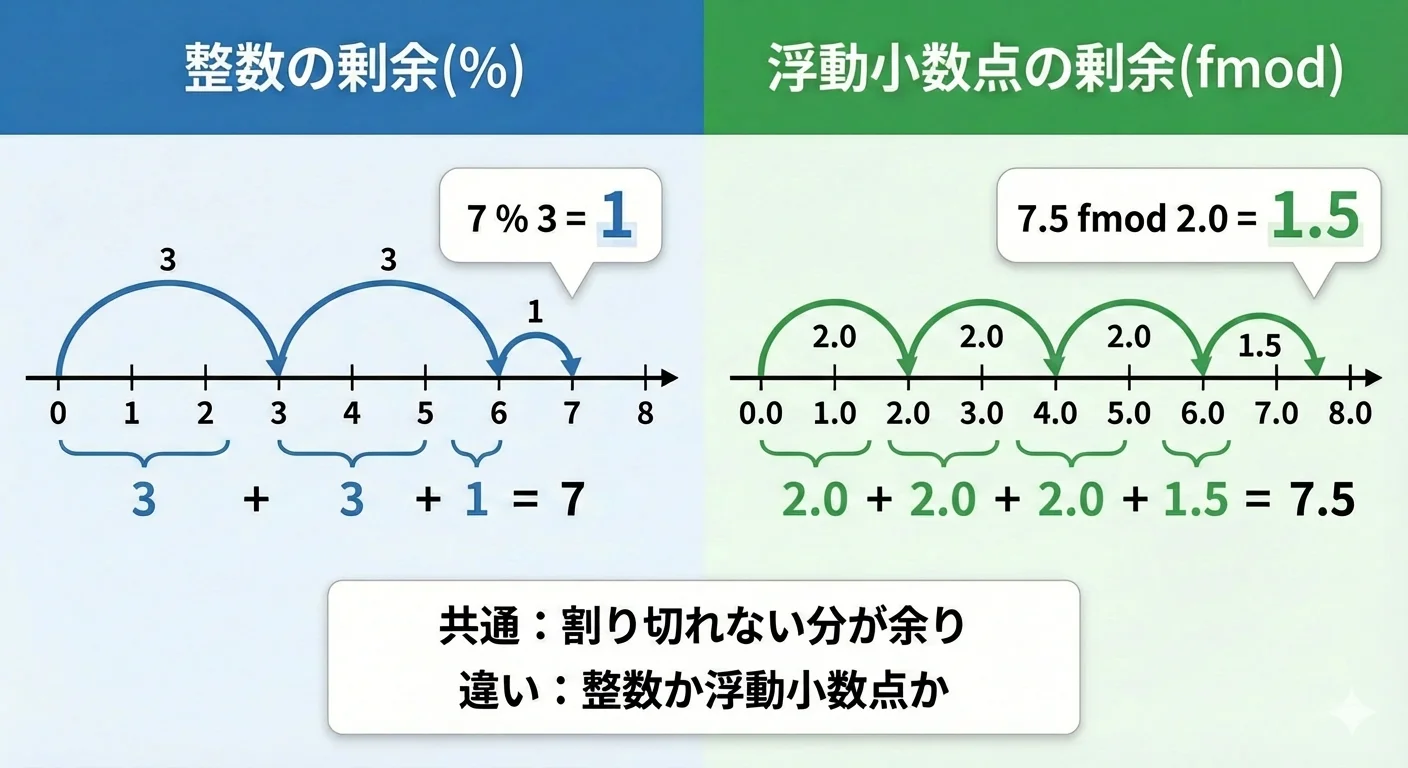
この図から、整数版の%cst-code>%と浮動小数点版のfmodは役割としては同じであることが直感的につかめます。
ただし、実際の計算は浮動小数点特有の誤差や、負数の扱いなどの違いが存在します。
fmodの数式的定義と性質
数式としてのfmod
切り捨て除算との関係
fmodの挙動は、次のように表すことができます。
fmod(x, y) = x – n * y
ここでnは「0に最も近い整数」です。
ここが「常に切り捨て」ではない点に注意が必要です。
- xとyが正の場合
→ 直感的な「切り捨て除算」と一致します - xまたはyが負の場合
→ 商nが0に近づくように選ばれるため、整数の/と%の組み合わせとは異なることがあります
fmodの戻り値と例外処理
正常なケースでの戻り値の範囲
戻り値の範囲のルール
fmod(x, y)の戻り値rは必ず次の条件を満たします。
fabs(r) < fabs(y)rの符号はxと同じ、またはゼロ
代表的な例を表でまとめます。
| x | y | fmod(x, y) | 備考 |
|---|---|---|---|
| 7.5 | 2.0 | 1.5 | 正の数同士 |
| -7.5 | 2.0 | -1.5 | xが負 → 戻りも負 |
| 7.5 | -2.0 | 1.5 | yが負でも余りの符号はxに従う |
| -7.5 | -2.0 | -1.5 | xと同符号 |
特殊ケース(ゼロ、NaN、無限大)
ゼロや無限大を含む場合の挙動
fmodは、引数が特定の値になると、未定義動作やNaNを返すことがあります。
代表的なケースを整理します。
| 条件 | 結果 |
|---|---|
| y == 0 | 未定義動作(多くはNaNや例外) |
| x が有限で、y が∞または-∞ | 戻り値は x (割り切れないので全体が余り) |
| x が∞または-∞で、y が有限かつ非ゼロ | NaN(定義不能) |
| どちらかがNaN | NaN |
[C言語標準ではy=0の時は未定義動作]とされているため、fmodを使う前にyが0でないことを必ず確認することが重要です。
fmodと整数剰余%cst-code>%の違いを詳しく比較
負の数を含む場合の挙動の違い
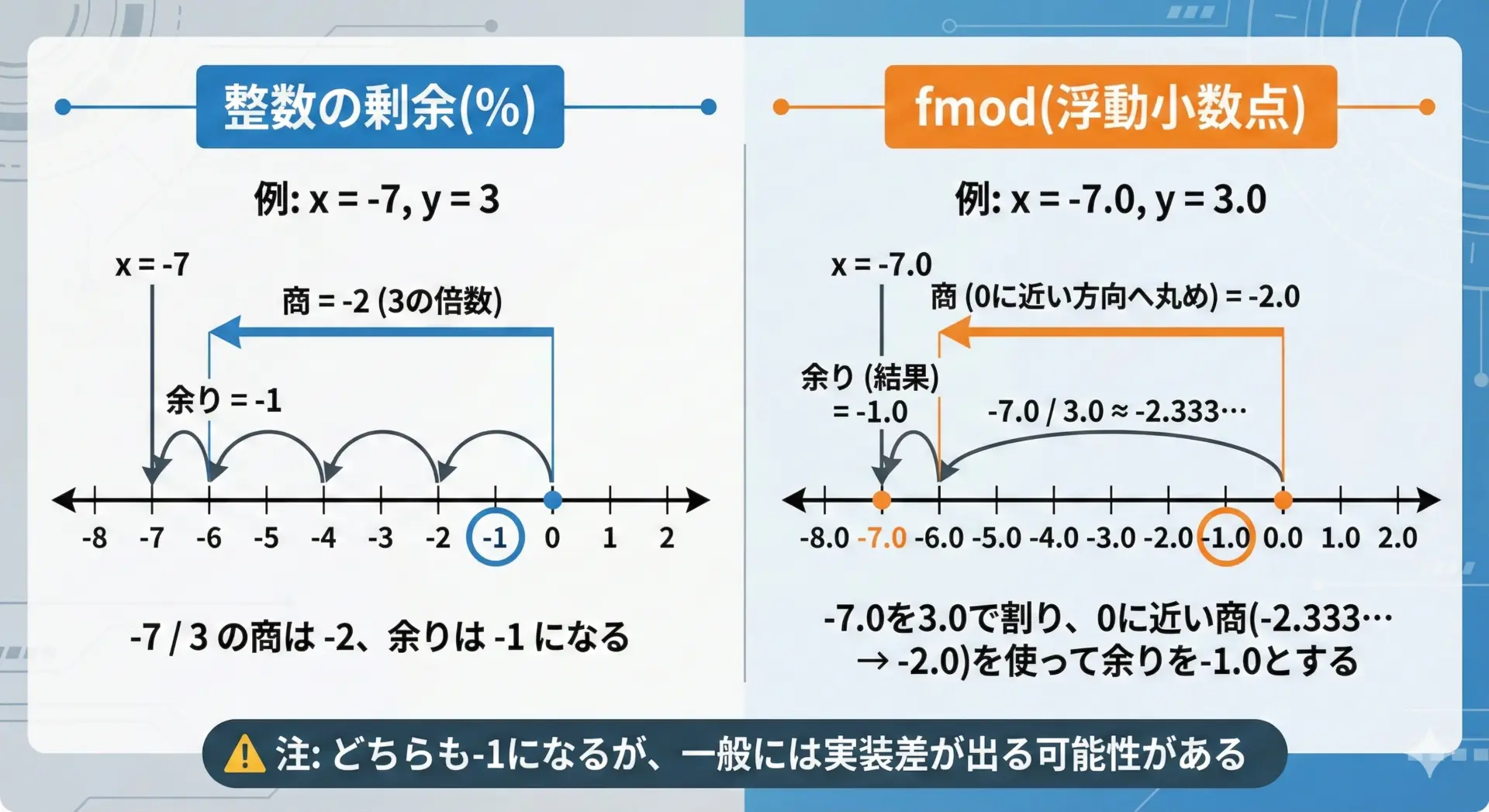
整数の%においては、C99以降では(a / b) * b + (a % b) == aが成り立つように定義されています。
一方、fmodでは「0に最も近い整数」を使うため、丸め方向が異なることで違いが出るケースもあります。
実際のコードで比較する
#include <stdio.h>
#include <math.h>
int main(void) {
int ai = -7, bi = 3;
double ad = -7.0, bd = 3.0;
// 整数の剰余
int ri = ai % bi;
// 浮動小数点の剰余
double rd = fmod(ad, bd);
printf("整数版: %d %% %d = %d\n", ai, bi, ri);
printf("浮動小数点版: fmod(%.1f, %.1f) = %.1f\n", ad, bd, rd);
return 0;
}整数版: -7 % 3 = -1
浮動小数点版: fmod(-7.0, 3.0) = -1.0この例では同じ結果になりますが、別の言語や別のライブラリ実装では負の剰余のルールが異なることも多いため、特に数値解析や物理シミュレーションでは挙動をきちんと把握しておく必要があります。
fmodの代表的な利用シーン
角度(ラジアン/度)の正規化
角度を一定範囲に収める
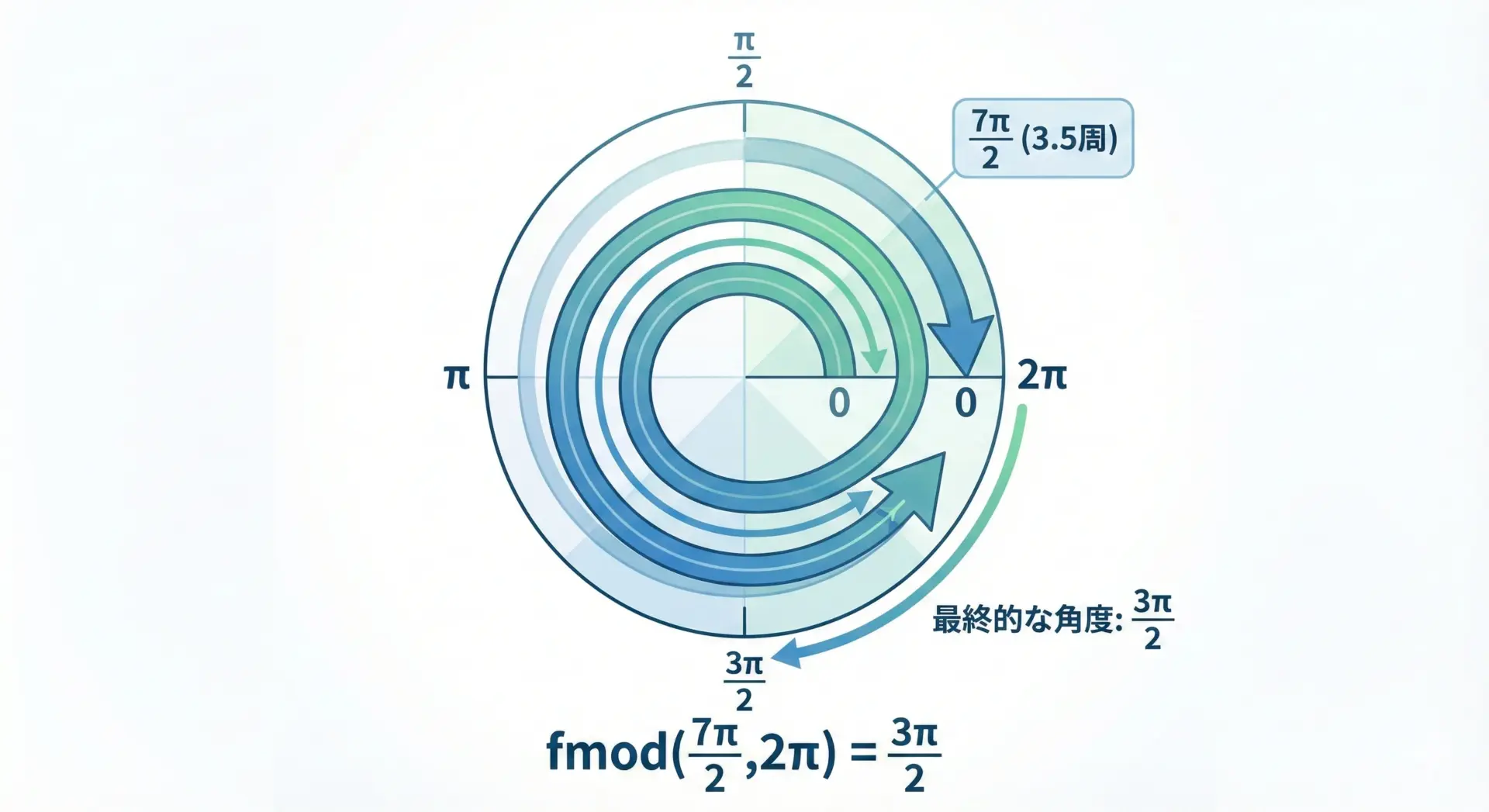
三角関数を扱う場面では、角度を0〜2πや-π〜πといった範囲に正規化する処理がよく登場します。
このときfmodは非常に有用です。
#include <stdio.h>
#include <math.h>
#define _USE_MATH_DEFINES // 一部環境ではM_PI定義用
#include <math.h>
int main(void) {
double angle = 7.0 * M_PI / 2.0; // 7π/2
// 0〜2π の範囲に正規化
double angle_norm = fmod(angle, 2.0 * M_PI);
if (angle_norm < 0) {
angle_norm += 2.0 * M_PI; // 負になった場合は2πを足す
}
printf("元の角度: %f rad\n", angle);
printf("正規化後: %f rad\n", angle_norm);
return 0;
}元の角度: 10.995574 rad
正規化後: 4.712389 radこの例では7π/2が3π/2に正規化されています。
周期的な処理(アニメーションや信号処理)
周期性を持つ現象(アニメーションのループ、波形の位相など)では、一定の周期で値を折り返す処理がよく使われます。
これもfmodの得意分野です。
#include <stdio.h>
#include <math.h>
int main(void) {
double t; // 時刻
double period = 5; // 周期(5秒ごとに同じ動きを繰り返す想定)
for (t = 0; t <= 12; t += 1.0) {
// 現在の時刻を周期で折り返した位相
double phase = fmod(t, period);
printf("t = %.1f sec, phase = %.1f sec\n", t, phase);
}
return 0;
}t = 0.0 sec, phase = 0.0 sec
t = 1.0 sec, phase = 1.0 sec
t = 2.0 sec, phase = 2.0 sec
t = 3.0 sec, phase = 3.0 sec
t = 4.0 sec, phase = 4.0 sec
t = 5.0 sec, phase = 0.0 sec
t = 6.0 sec, phase = 1.0 sec
t = 7.0 sec, phase = 2.0 sec
t = 8.0 sec, phase = 3.0 sec
t = 9.0 sec, phase = 4.0 sec
t = 10.0 sec, phase = 0.0 sec
t = 11.0 sec, phase = 1.0 sec
t = 12.0 sec, phase = 2.0 secこのように、周期処理では「時間tを周期で割った余り」を使ってループを実現することが多いです。
fmod使用時の注意点と落とし穴
浮動小数点誤差と「きっちり0にならない」問題
浮動小数点計算では、理論上は0になるはずの結果が、非常に小さい値として残ることがあります。
fmodでも同様です。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 0.3;
double y = 0.1;
double r = fmod(x, y);
printf("fmod(%.17f, %.17f) = %.17f\n", x, y, r);
return 0;
}fmod(0.30000000000000004, 0.10000000000000001) = 0.00000000000000000環境によっては完全に0になる場合もありますが、別の組み合わせではごく小さな値が残る場合があります。
このため、「fmodの結果が0かどうか」を厳密な比較== 0.0で判断しないほうが安全です。
例えば、次のようにfabs(r) < 1e-9のような「許容誤差」を設けて比較する方法が実用的です。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 1.0;
double y = 0.1;
double r = fmod(x, y);
double eps = 1e-9;
if (fabs(r) < eps) {
printf("ほぼ割り切れているとみなす\n");
} else {
printf("余りがあるとみなす: r = %.17f\n", r);
}
return 0;
}ほぼ割り切れているとみなす0除算と未定義動作への注意
すでに述べたとおり、第2引数yが0の場合、fmodの動作は未定義です。
プログラムがクラッシュしたり、予測不能な値が返る可能性があります。
fmodを呼ぶ前に必ずyが0でないかチェックすることを習慣にすると安全です。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 5.0;
double y = 0.0;
if (y == 0.0) {
printf("エラー: 0で割ることはできません\n");
return 1;
}
double r = fmod(x, y);
printf("fmod(%.2f, %.2f) = %.2f\n", x, y, r);
return 0;
}エラー: 0で割ることはできませんfmodのバリエーション(fmodf, fmodl)と型の扱い
fmod / fmodf / fmodl を使い分ける理由
C標準では、型に応じて次の3種類が用意されています。
| 関数名 | 引数と戻り値の型 | 主な用途 |
|---|---|---|
| fmod | double | 一般的な用途 |
| fmodf | float | 単精度が必要な場合 |
| fmodl | long double | 拡張精度が必要な場合 |
基本的にはdouble用のfmodを使えば十分ですが、組み込み環境や性能が重要な場面ではfloatで揃えるためにfmodfを使うこともあります。
型変換に注意したサンプル
#include <stdio.h>
#include <math.h>
int main(void) {
float xf = 7.5f;
float yf = 2.0f;
// NG例: floatをdoubleに暗黙変換してからfmodし、戻りをfloatに戻す
float rf_ng = fmod(xf, yf); // 実際にはfmod(double, double)が呼ばれる
// OK例: 型に合わせてfmodfを使う
float rf_ok = fmodf(xf, yf); // fmodf(float, float)が呼ばれる
printf("NG例 (fmod): %.6f\n", rf_ng);
printf("OK例 (fmodf): %.6f\n", rf_ok);
return 0;
}NG例 (fmod): 1.500000
OK例 (fmodf): 1.500000この例では結果は同じですが、常に型を揃えた関数を使うことで、不要な型変換や性能低下を防ぐことができます。
実践的な応用例
アニメーションで位置をループさせる

#include <stdio.h>
#include <math.h>
int main(void) {
double position = 0.0; // オブジェクトの位置
double speed = 7.3; // 速度
double width = 100.0; // 画面幅
for (int i = 0; i < 20; ++i) {
// 1フレームごとに位置を更新
position += speed;
// 画面幅を超えたら折り返す
position = fmod(position, width);
if (position < 0) {
position += width;
}
printf("frame %2d: position = %6.2f\n", i, position);
}
return 0;
}frame 0: position = 7.30
frame 1: position = 14.60
frame 2: position = 21.90
frame 3: position = 29.20
frame 4: position = 36.50
frame 5: position = 43.80
frame 6: position = 51.10
frame 7: position = 58.40
frame 8: position = 65.70
frame 9: position = 73.00
frame 10: position = 80.30
frame 11: position = 87.60
frame 12: position = 94.90
frame 13: position = 2.20
frame 14: position = 9.50
frame 15: position = 16.80
frame 16: position = 24.10
frame 17: position = 31.40
frame 18: position = 38.70
frame 19: position = 46.00位置が100.0を超えた時点で0〜100の範囲内に折り返されていることがわかります。
秒数から「時:分:秒」を求める
整数で実装することが多い処理ですが、浮動小数点で時間を扱う場合にもfmodが役立ちます。

#include <stdio.h>
#include <math.h>
int main(void) {
double total_seconds = 3661.75; // 1時間1分1.75秒
// 時
int hours = (int)(total_seconds / 3600.0);
double remainder = fmod(total_seconds, 3600.0);
// 分
int minutes = (int)(remainder / 60.0);
double seconds = fmod(remainder, 60.0);
printf("total = %.2f sec\n", total_seconds);
printf("%d 時間 %d 分 %.2f 秒\n", hours, minutes, seconds);
return 0;
}total = 3661.75 sec
1 時間 1 分 1.75 秒ここでは、大きな単位から順番に「商」と「余り」を取り出すことで、人間にとって扱いやすい「時:分:秒」の形に変換しています。
まとめ
fmodは、C言語で浮動小数点の剰余を求めるための標準的な関数です。
整数の%と同じ発想で使えますが、戻り値の符号やゼロ・無限大の扱い、浮動小数点誤差など、注意すべき点もあります。
角度の正規化や周期処理、位置ループなど、実践的な用途も多く、使いこなせば表現できる処理の幅が大きく広がります。
この記事を参考に、目的に応じてfmodやfmodfを適切に選び、安全で分かりやすいコードを書くことを意識してみてください。

