閉じる

C言語のtrunc関数の使い方・注意点を解説【小数切り捨て】

広告

C言語で小数の切り捨てを行うとき、trunc関数を正しく理解しておくと、安全かつ意図通りの結果を得やすくなります。

似た関数であるfloorやceil、丸めを行うroundとの違いを整理しながら、truncの基本から注意点、C99以前での代替方法まで、実用的な観点で詳しく解説します。

目次 [ close ]
  1. trunc関数とは？
    1. trunc関数の役割と特徴
    2. floor・ceil・roundとの違い
    3. C標準規格(math.h)での位置づけ
  2. trunc関数の基本的な使い方
    1. 関数プロトタイプとインクルードファイル
    2. trunc・truncf・trunclの違い
    3. 基本的な使用例
    4. 正と負の値の切り捨て動作の確認
  3. trunc関数の注意点と落とし穴
    1. 負の小数をtruncする際の挙動
    2. オーバーフロー・未定義動作に注意
    3. NaN・無限大(INFINITY)を渡した場合の結果
    4. 浮動小数点誤差と期待値のずれ
    5. キャスト(int)との違いと使い分け
  4. trunc関数の活用例と代替手段
    1. 小数切り捨てを使う典型的な場面
    2. 小数第n位での切り捨てを行う方法
    3. C99以前でtruncが使えない場合の実装例
    4. floor関数や型変換との比較と選び方
  5. まとめ

trunc関数とは？

trunc関数の役割と特徴

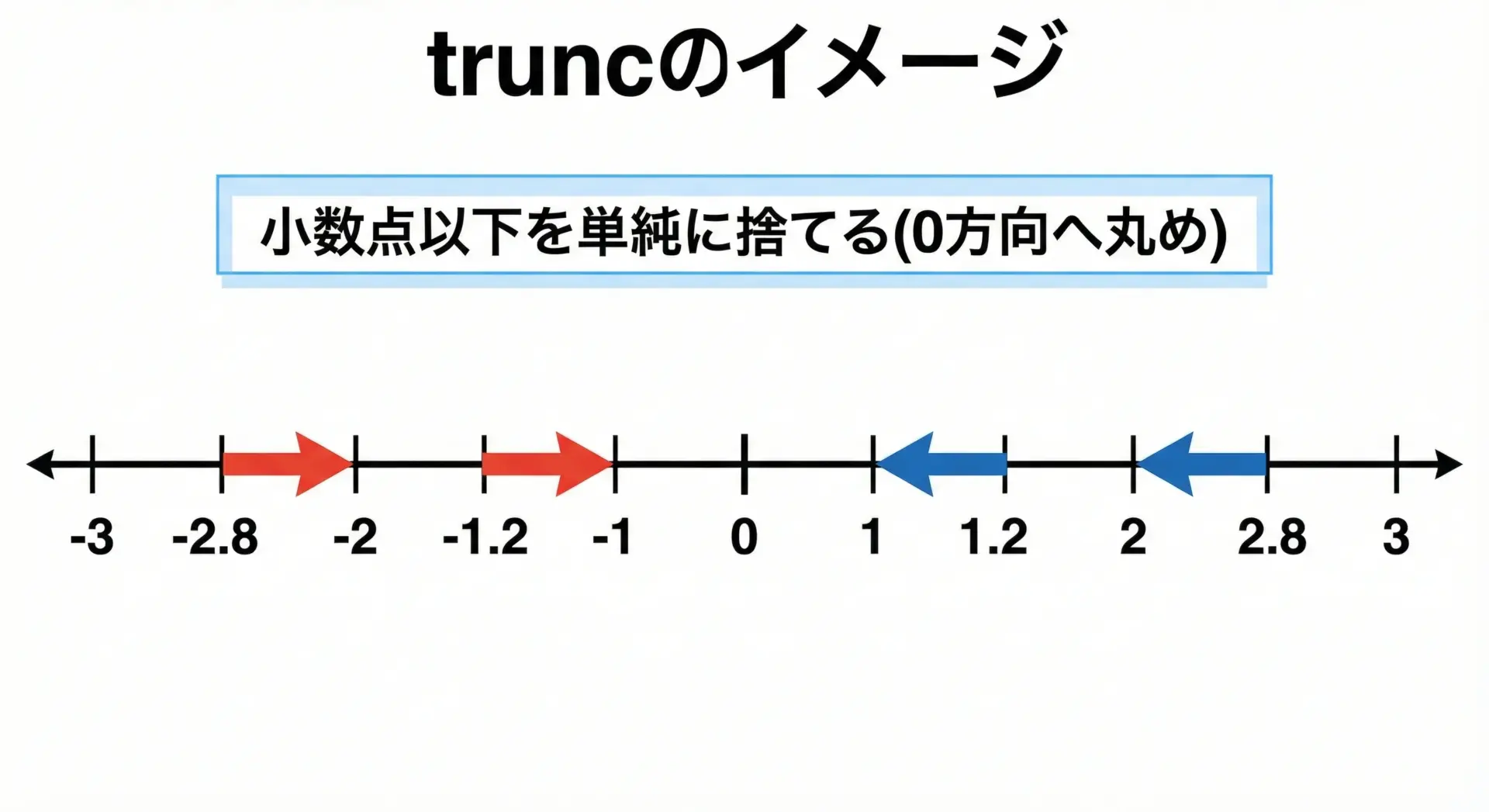
trunc関数は、浮動小数点数の小数部分を切り捨てて整数部分だけを残すための関数です。

ここでの「切り捨て」は、数学の床関数(floor)のように常に小さい側へではなく、0に近づく方向に向かって丸めることを意味します。

たとえば、次のような結果になります。

  • 7 → 1.0
  • 2 → 1.0
  • −1.7 → −1.0
  • −1.2 → −1.0

このように、正の数に対しても負の数に対しても、小数点以下を単純に削除していると考えると理解しやすくなります。

floor・ceil・roundとの違い

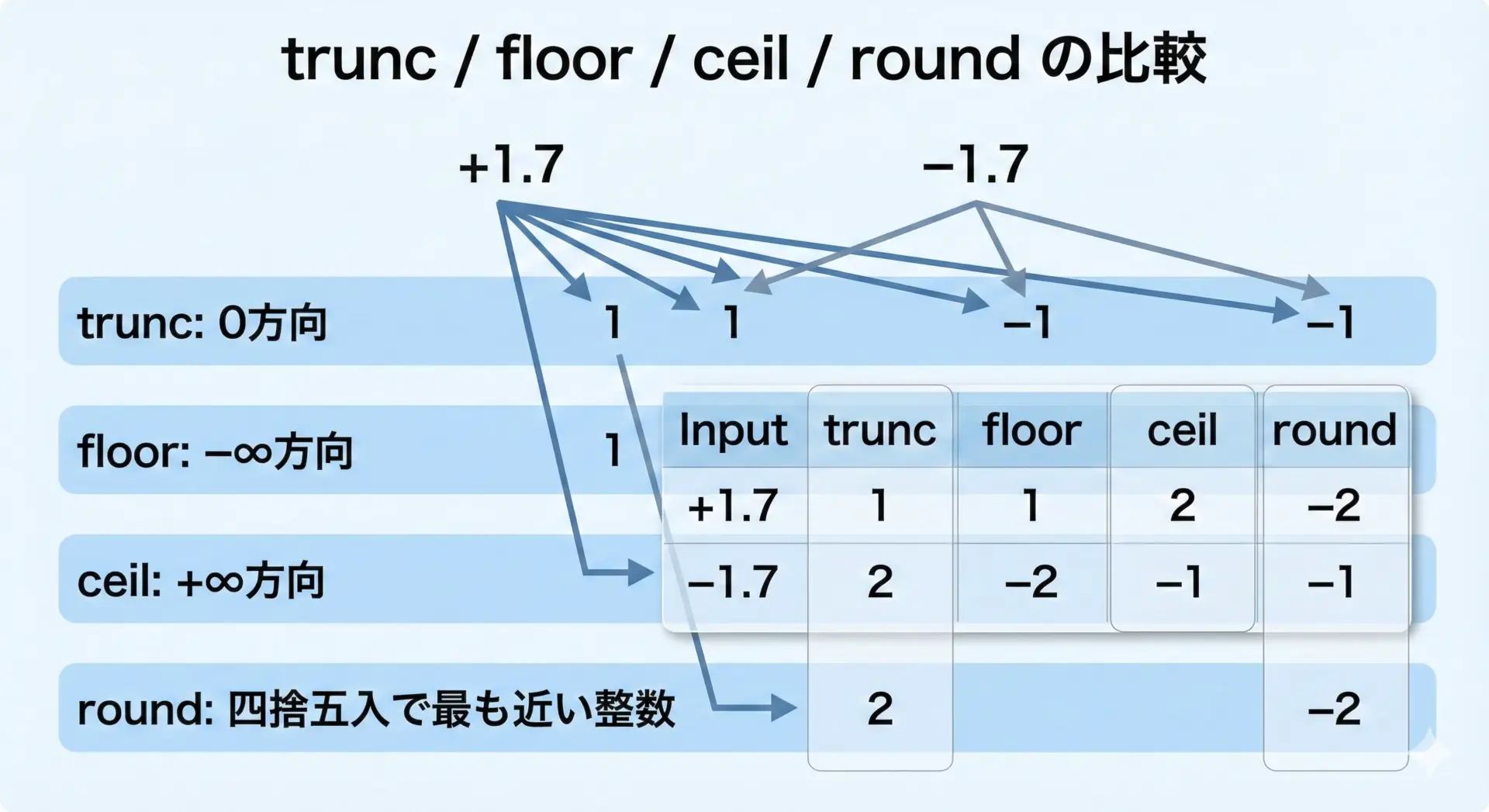
truncは、よく使われるfloorやceil、roundと混同されがちです。

違いを明確にするため、典型的な値で比較してみます。

入力値関数結果動作の方向
1.7trunc1.00方向
1.7floor1.0−∞方向
1.7ceil2.0+∞方向
1.7round2.0近い整数
−1.7trunc−1.00方向
−1.7floor−2.0−∞方向
−1.7ceil−1.0+∞方向
−1.7round−2.0近い整数

truncは「0方向への丸め」であり、絶対値を小さくする働きをします。

それに対して、

  • floorは小さい側(−∞方向)へ丸める
  • ceilは大きい側(+∞方向)へ丸める
  • roundは最も近い整数に丸める(0.5の扱いは実装依存の場合あり)

と方向性が異なります。

C標準規格(math.h)での位置づけ

truncはC99以降のC標準規格でmath.hに追加された関数です。

浮動小数点専用の数学関数であり、整数型には直接は使えません。

C標準ライブラリでは、truncには次の3種類が定義されています。

  • double trunc(double x);
  • float truncf(float x);
  • long double truncl(long double x);

これらはいずれも小数部を切り捨てた同じ実数値を返しますが、扱う精度と型が異なります。

trunc関数の基本的な使い方

関数プロトタイプとインクルードファイル

trunc系の関数を使うには、必ずmath.hをインクルードし、リンク時に数学ライブラリを指定する必要があります(UNIX系環境など)。

関数プロトタイプは次のように定義されています。

C言語
/* math.h より(概略) */

double      trunc(double x);
float       truncf(float x);
long double truncl(long double x);

利用する際は、最低限次のようなヘッダ指定が必要です。

C言語
#include <stdio.h>
#include <math.h>

UNIX系環境(gccなど)では、コンパイル時に-lmオプションで数学ライブラリをリンクすることが一般的です。

Shell
gcc sample.c -o sample -lm

trunc・truncf・trunclの違い

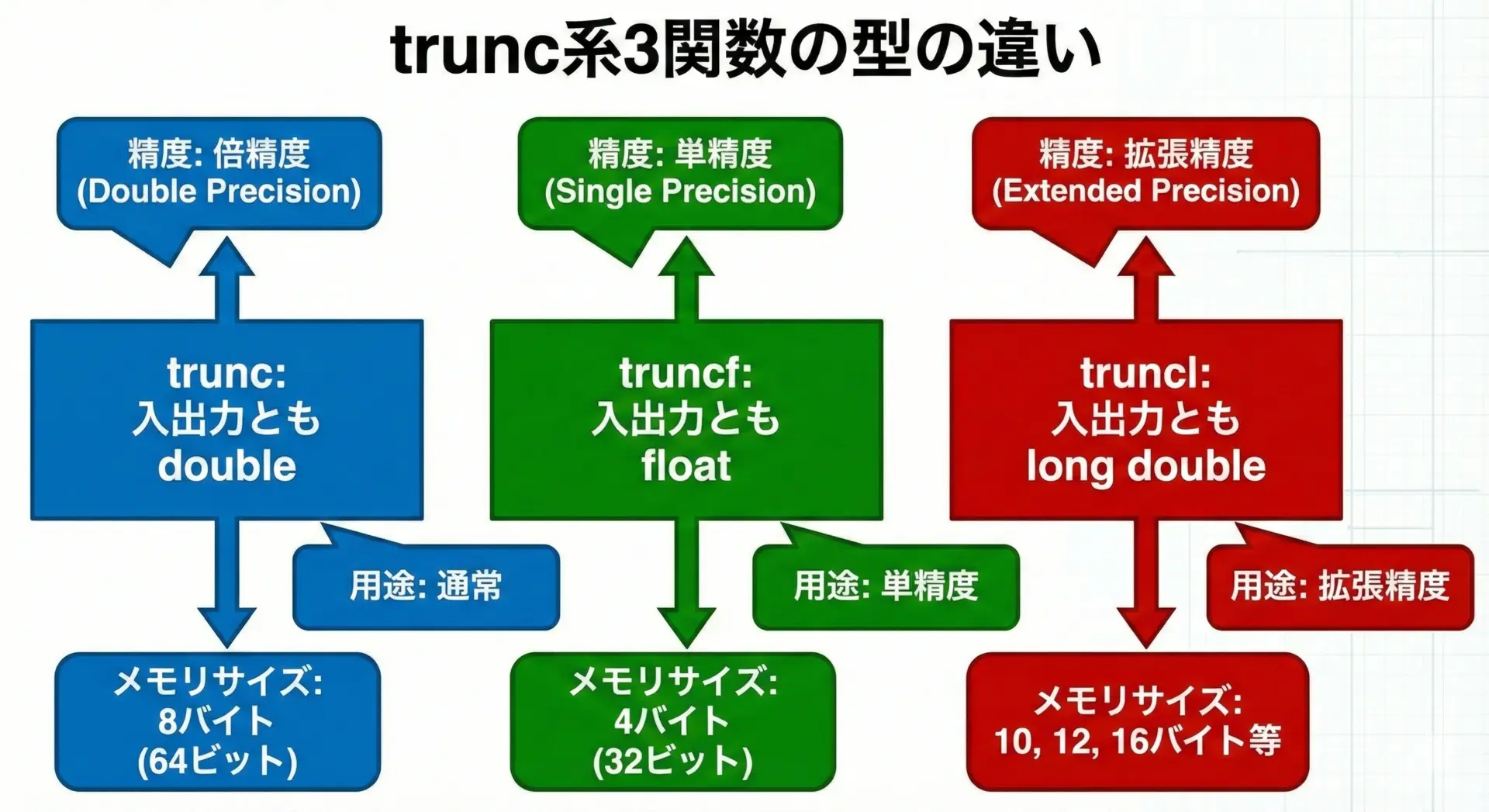
truncファミリは入力型と戻り値の型が揃っていることが特徴です。

  • trunc
    引数と戻り値がdouble。最もよく使われる標準的な形です。
  • truncf
    引数と戻り値がfloat。単精度で済む場合や、浮動小数点演算をfloatで統一したい場合に使います。
  • truncl
    引数と戻り値がlong double。より高い精度や拡張精度が必要な場合に使います。

変数の型に合わせた関数を使うことで、無用な型変換を防ぎ、精度低下や警告の発生を抑えることができます。

基本的な使用例

C言語
#include <stdio.h>
#include <math.h>

int main(void) {
    double  a = 3.14159;
    float   b = -2.71828f;
    long double c = 123.987L;

    // double 用の trunc
    double  ta = trunc(a);      // 3.0

    // float 用の truncf
    float   tb = truncf(b);     // -2.0f

    // long double 用の truncl
    long double tc = truncl(c); // 123.0L

    printf("trunc(%.5f)   = %.5f\n", a, ta);
    printf("truncf(%.5f)  = %.5f\n", b, tb);
    printf("truncl(%.3Lf) = %.3Lf\n", c, tc);

    return 0;
}
実行結果
trunc(3.14159)   = 3.00000
truncf(-2.71828) = -2.00000
truncl(123.987)  = 123.000

この例では、それぞれの型に対応したtrunc系関数を呼び出しています。

戻り値も同じ型になるため、そのまま同じ型の変数に代入できます。

正と負の値の切り捨て動作の確認

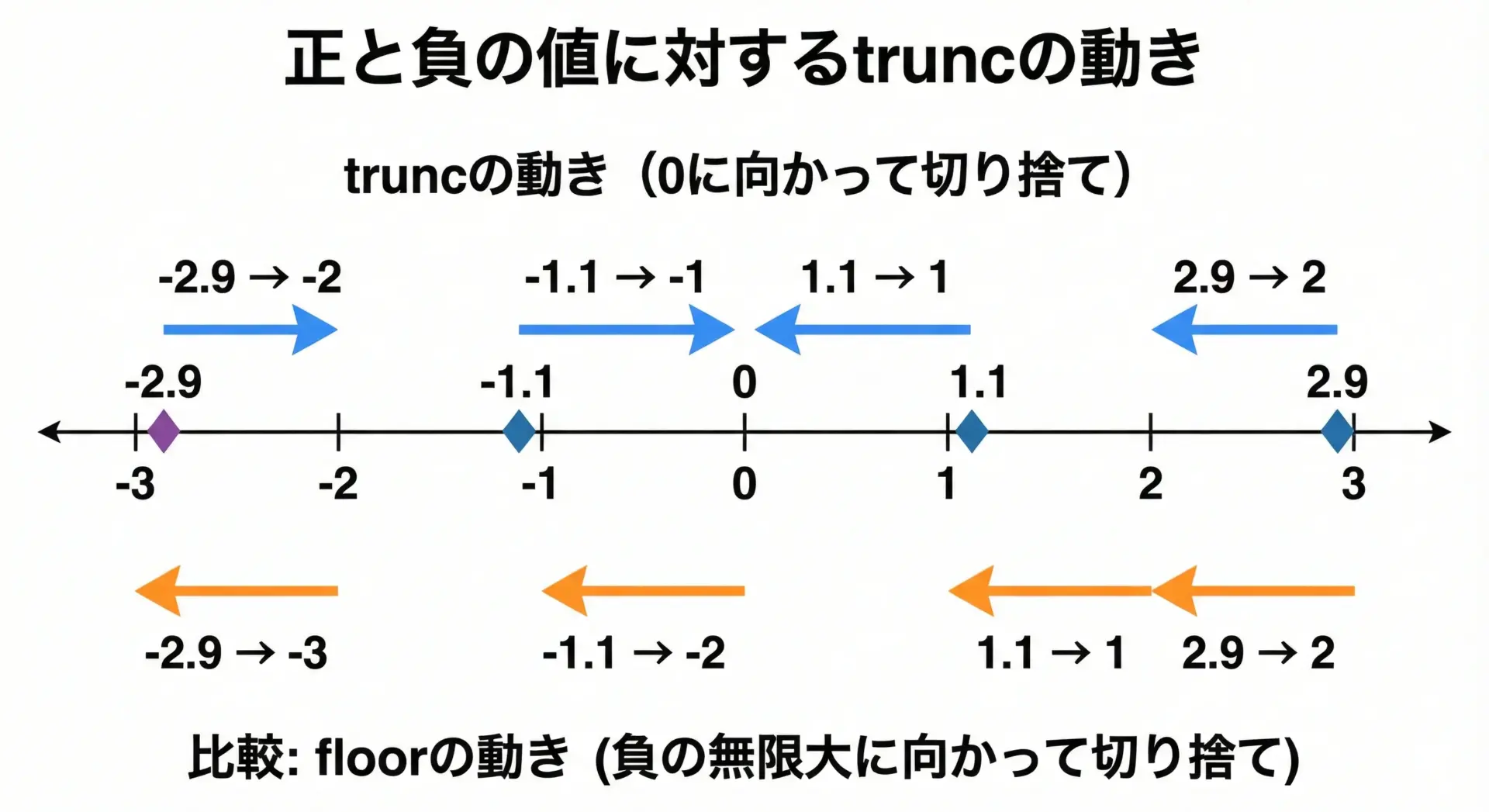
正負で挙動が変わるfloorと違い、truncは常に0へ近づけることがポイントです。

サンプルコードで確認してみます。

C言語
#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { 2.9, 1.1, 0.0, -1.1, -2.9 };
    int i;

    for (i = 0; i < 5; i++) {
        double x = values[i];
        printf("x = %5.1f, trunc(x) = %5.1f\n", x, trunc(x));
    }

    return 0;
}
実行結果
x =   2.9, trunc(x) =   2.0
x =   1.1, trunc(x) =   1.0
x =   0.0, trunc(x) =   0.0
x =  -1.1, trunc(x) =  -1.0
x =  -2.9, trunc(x) =  -2.0

符号は変わらず、絶対値だけが小さくなることが確認できます。

trunc関数の注意点と落とし穴

負の小数をtruncする際の挙動

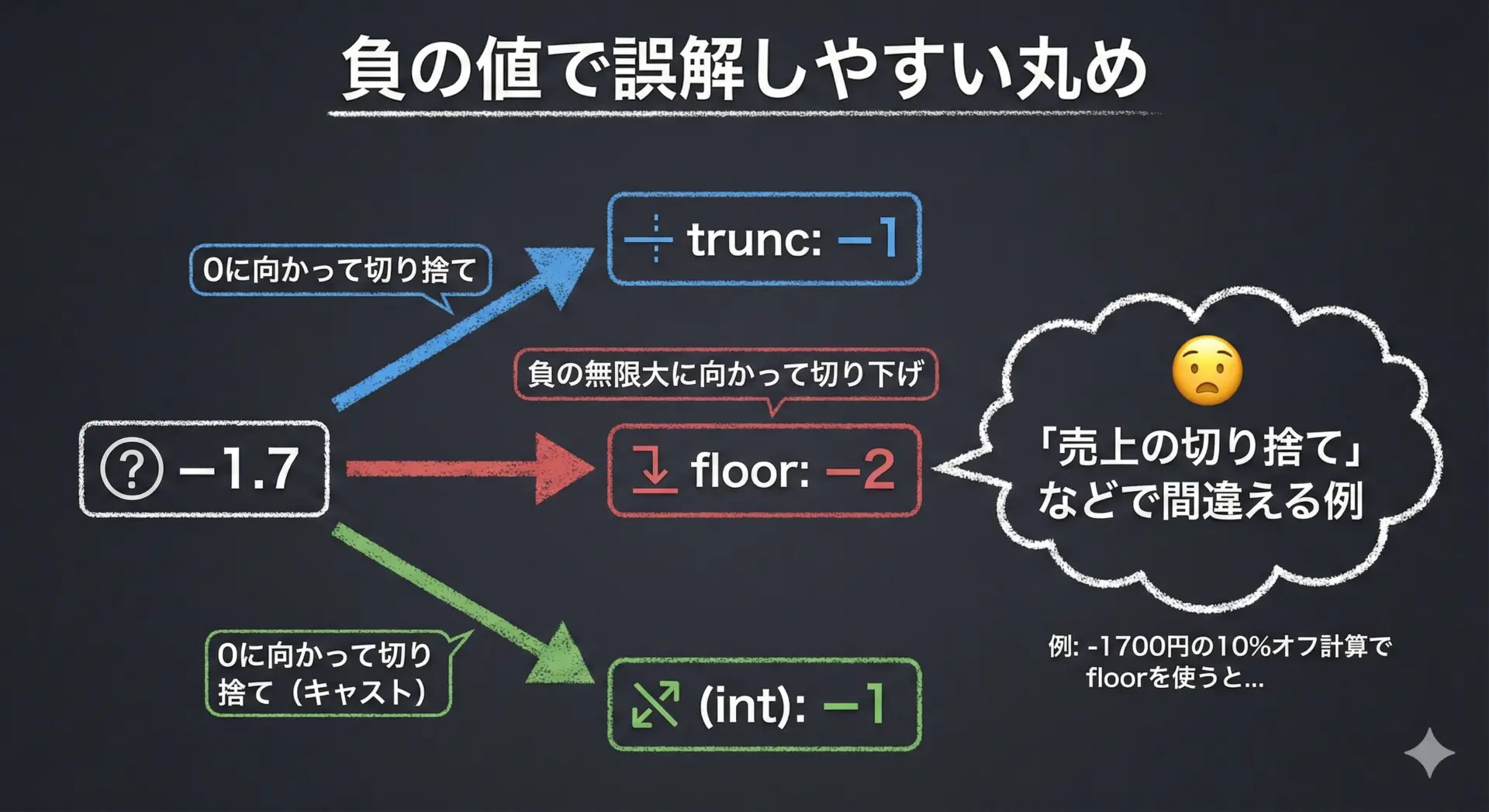
負の値に対してfloorと混同すると、計算結果を大きく誤る可能性があります。

たとえば、「常に実際の値以下で見積もりたい」といった要件がある場合、truncではなくfloorを使う必要があります。

  • −1.7の「以下の整数」という条件なら、正解は−2ですが、
  • trunc(−1.7)は−1であり、「以下の整数」という条件を満たしません。

「切り捨て」という日本語表現だけで関数を選ぶのは危険であり、どの方向に丸めるかを常に意識することが大切です。

オーバーフロー・未定義動作に注意

trunc自体は浮動小数点の範囲内で動作するため、引数や戻り値が浮動小数点の範囲を大きく超えてしまうことは通常ありません。

しかし、truncした結果を整数型へキャストするときに注意が必要です。

C言語
#include <stdio.h>
#include <math.h>
#include <limits.h>

int main(void) {
    double x = 1e20;  // 非常に大きな値
    double tx = trunc(x);

    // int へキャストするとオーバーフローの危険
    int n = (int)tx;

    printf("x   = %.0f\n", x);
    printf("tx  = %.0f\n", tx);
    printf("INT_MAX = %d\n", INT_MAX);
    printf("n = %d (未定義動作の可能性)\n", n);

    return 0;
}
実行結果
x   = 100000000000000000000
tx  = 100000000000000000000
INT_MAX = 2147483647
n = 2147483647 (など不定)

上のコードでは、int型の表現範囲を超える値をキャストしており、C言語では未定義動作となります。

必要であれば、

  • LONG_MAXやLLONG_MAXと比較して範囲チェックを行う
  • そもそも整数型で表現しきれない値は整数に変換しない

といった対策が必要です。

NaN・無限大(INFINITY)を渡した場合の結果

浮動小数点にはNaN(非数)や±∞(無限大)という特別な値があります。

C99の規格に従う環境では、truncはこれらに対して次のような結果を返します。

入力値結果
NaNNaN
+INFINITY+INFINITY
−INFINITY−INFINITY

実際に動作を確認する例を示します。

C言語
#include <stdio.h>
#include <math.h>

int main(void) {
    double nan_val = NAN;
    double inf_pos = INFINITY;
    double inf_neg = -INFINITY;

    printf("trunc(NAN)       = %f\n", trunc(nan_val));
    printf("trunc(INFINITY)  = %f\n", trunc(inf_pos));
    printf("trunc(-INFINITY) = %f\n", trunc(inf_neg));

    return 0;
}
実行結果
trunc(NAN)       = nan
trunc(INFINITY)  = inf
trunc(-INFINITY) = -inf

NaNはNaNのまま、∞は∞のままであり、truncによって有限値に変化することはありません。

浮動小数点誤差と期待値のずれ

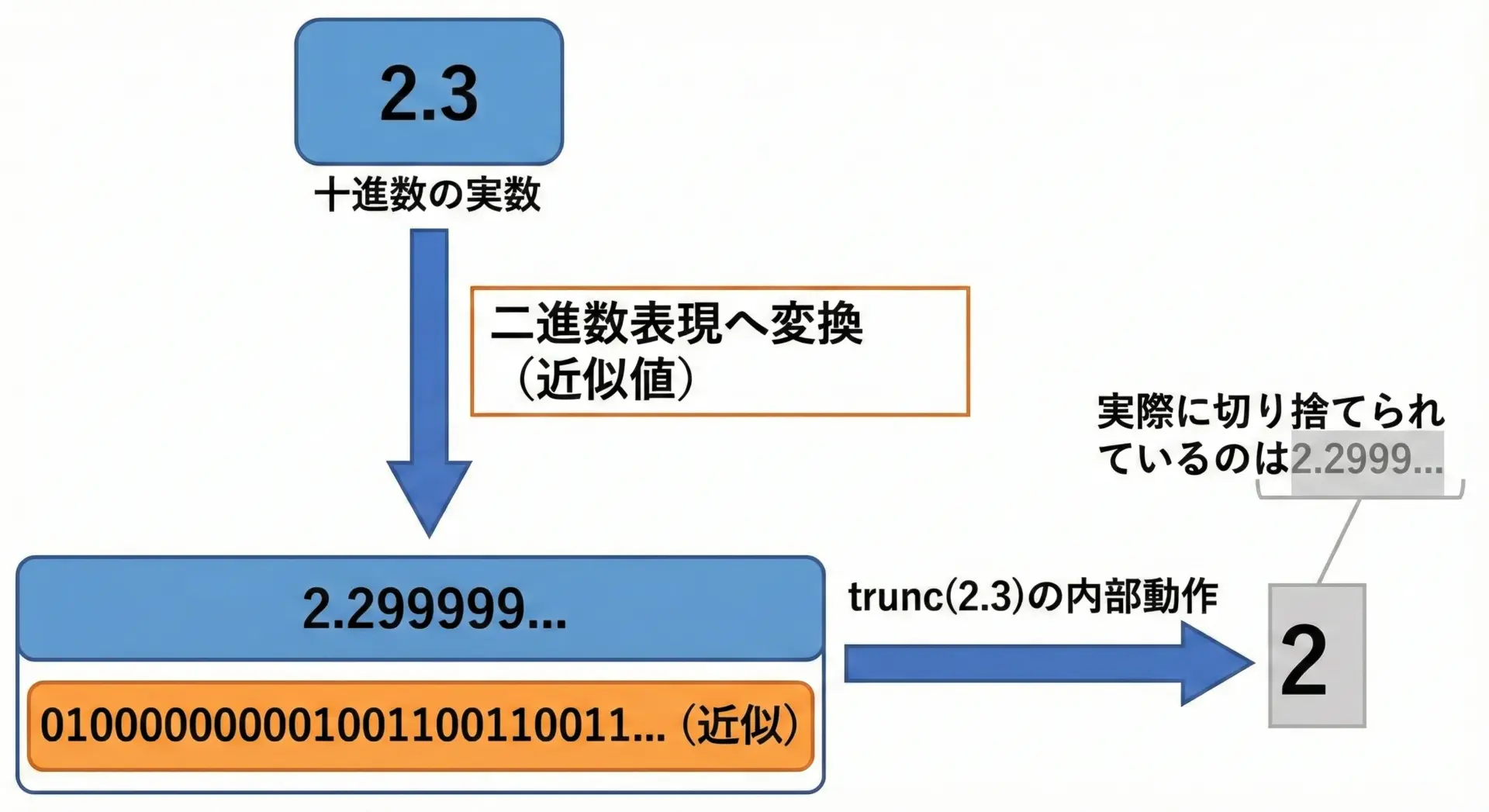
浮動小数点数は2進表現での近似値として内部に保存されているため、「2.3」などが正確に表現できないことがあります。

このため、理論上はtrunc(2.3)が2.0になるはずでも、環境や表示の仕方によって2.000000ではなく1.999999と表示されるようなことが起き得ます。

C言語
#include <stdio.h>
#include <math.h>

int main(void) {
    double x = 2.3;
    double tx = trunc(x);

    printf("x  = %.17f\n", x);
    printf("tx = %.17f\n", tx);

    return 0;
}
実行結果
x  = 2.2999999999999998
tx = 2.0000000000000000

この例では幸い期待通りですが、入力値が既に誤差を含んでいることがわかります。

trunc自身が「誤差を増やす」わけではありませんが、「10進の感覚通りに丸められていない」ように見える原因は、多くの場合「もともとの浮動小数点表現の近似」にあります。

キャスト(int)との違いと使い分け

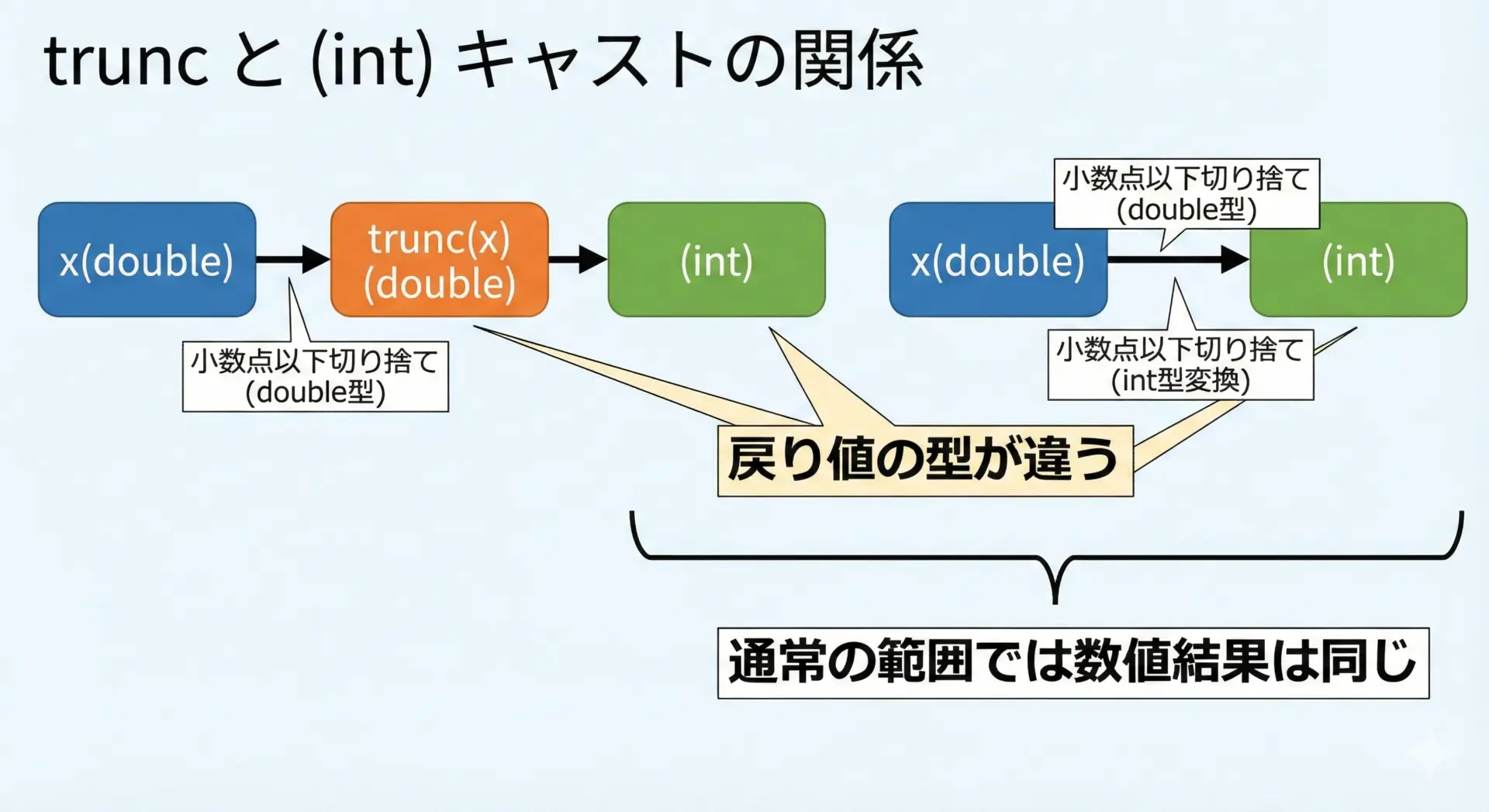
多くのケースで、truncと整数へのキャストは数値的には同じ動作をします。

  • (int)x
    0方向へ丸められた整数値をintとして返す
  • trunc(x)
    0方向へ丸められた値をdoubleとして返す

たとえば、次のような比較ができます。

C言語
#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { 3.9, -3.9 };
    int i;

    for (i = 0; i < 2; i++) {
        double x = values[i];
        int    n = (int)x;       // キャスト
        double t = trunc(x);     // trunc

        printf("x = %4.1f, (int)x = %3d, trunc(x) = %4.1f\n", x, n, t);
    }

    return 0;
}
実行結果
x =  3.9, (int)x =   3, trunc(x) =  3.0
x = -3.9, (int)x =  -3, trunc(x) = -3.0

値としては一致していますが、戻り値の型が異なる点が大きな違いです。

  • 演算をさらに浮動小数点で続けたい場合はtruncを使う
  • 整数として扱いたい場合はキャストを使う

また、前述の通り、大きな値をintにキャストする場合にはオーバーフローによる未定義動作の問題がありますが、truncだけで完結している限りはそのような問題は発生しにくいという違いもあります。

trunc関数の活用例と代替手段

小数切り捨てを使う典型的な場面

truncによる小数切り捨ては、次のような場面でよく使われます。

  • 座標・ピクセル位置の計算で、小数を含む論理座標から整数の画面座標へ変換する
    (ただし、単純なキャストで足りるケースも多い)
  • 金額や数量の概算として、「何個分相当か」を求める
    (営業日数のざっくり計算などで、端数を無視する目的)
  • ログ出力や表示で、「小数以下は気にしない」粗い情報を出したいとき

たとえば、ダウンロード進捗をざっくりと表示したい例を考えます。

C言語
#include <stdio.h>
#include <math.h>

int main(void) {
    double total = 1024.0; // 総サイズ(KB)
    double done  = 350.7;  // ダウンロード済み(KB)

    double ratio = done / total * 100.0; // 進捗率(%) 小数あり
    double shown = trunc(ratio);         // 小数以下切り捨て

    printf("progress: %.1f%% (shown: %.0f%%)\n", ratio, shown);

    return 0;
}
実行結果
progress: 34.3% (shown: 34%)

このように、「あくまで目安であり、きっちりした丸めは不要」な場面でtruncは扱いやすくなります。

小数第n位での切り捨てを行う方法

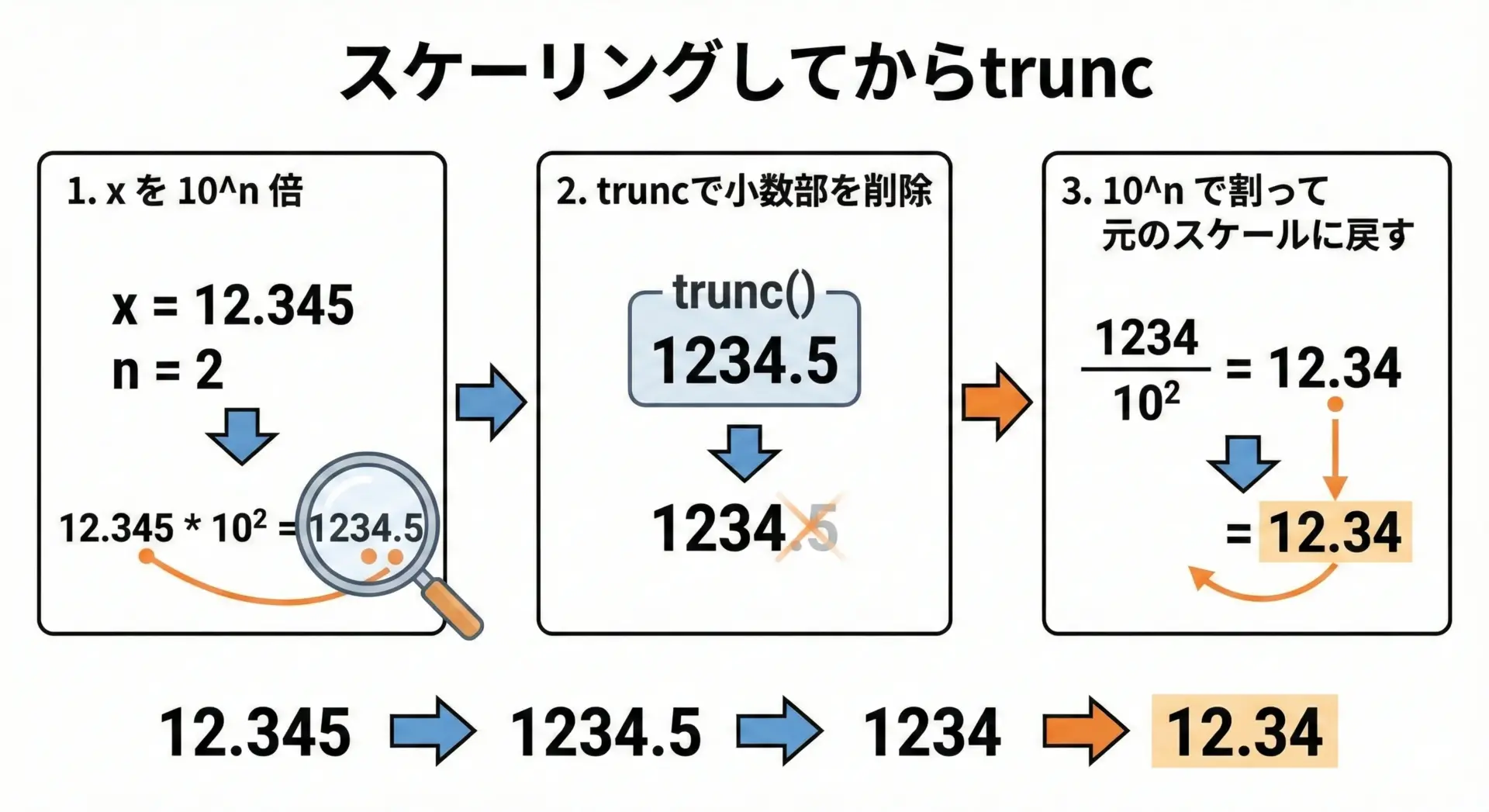
truncは「整数への切り捨て」しか行いませんが、少数第n位で切り捨てたい場合も、スケーリングを組み合わせれば実現できます。

考え方はシンプルで、

  1. 値を10^n倍する
  2. truncで小数部を切り捨てる
  3. 10^nで割って元の桁に戻す

という手順になります。

C言語
#include <stdio.h>
#include <math.h>

// x を、小数第 n 位で切り捨てる関数
double trunc_to_nth(double x, int n) {
    double scale = pow(10.0, n);  // 10^n を計算
    double y = x * scale;         // n桁左にずらす
    y = trunc(y);                 // 小数部を切り捨て
    return y / scale;             // 元のスケールに戻す
}

int main(void) {
    double x = 12.34567;

    printf("x               = %.5f\n", x);
    printf("小数第1位切り捨て = %.5f\n", trunc_to_nth(x, 1)); // 12.3
    printf("小数第2位切り捨て = %.5f\n", trunc_to_nth(x, 2)); // 12.34
    printf("小数第3位切り捨て = %.5f\n", trunc_to_nth(x, 3)); // 12.345

    return 0;
}
実行結果
x               = 12.34567
小数第1位切り捨て = 12.30000
小数第2位切り捨て = 12.34000
小数第3位切り捨て = 12.34500

ただし、ここでも浮動小数点の誤差や、powによる誤差累積の可能性があるため、金額計算など厳密な精度が必要な場合には整数で金額(例えば「円」ではなく「銭」単位)を扱うなどの対策を検討してください。

C99以前でtruncが使えない場合の実装例

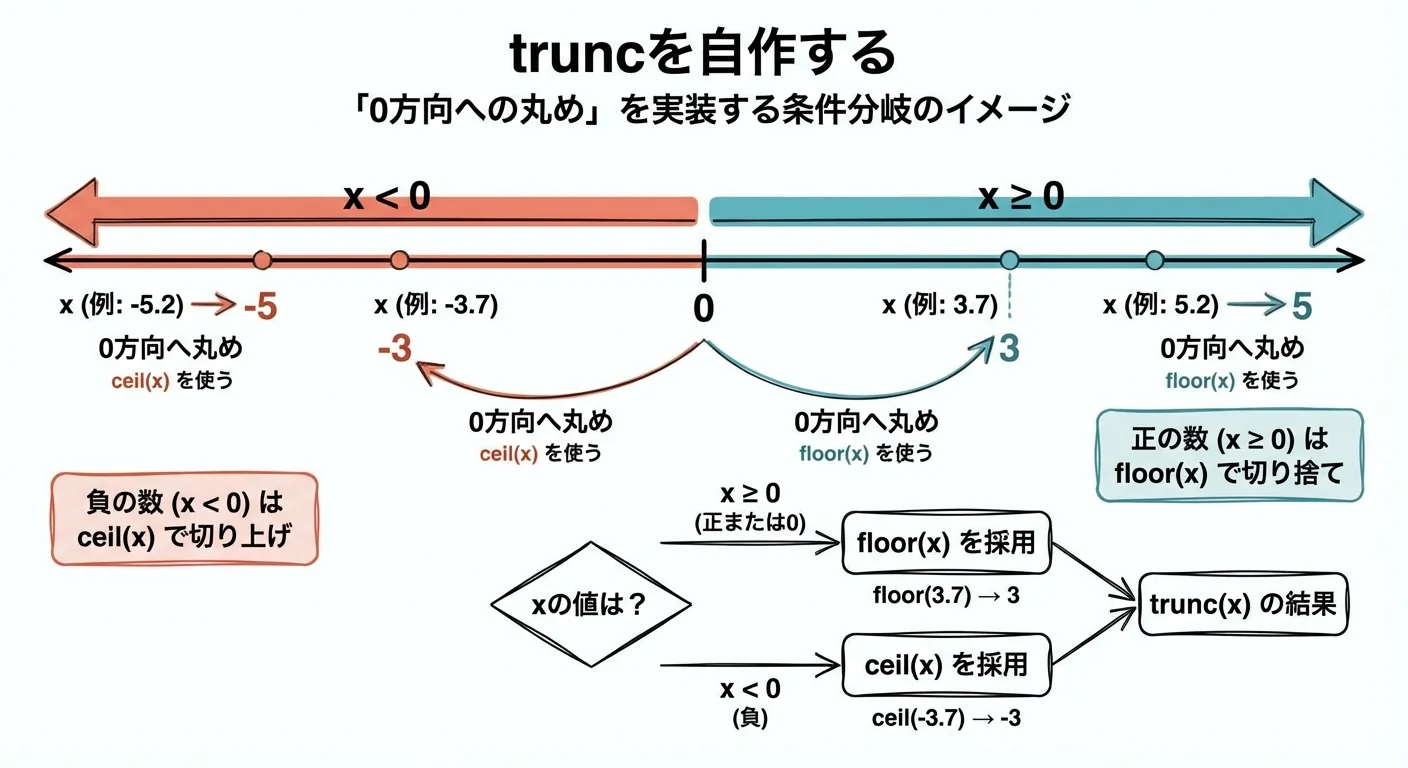
C99に対応していないコンパイラや、古い環境ではtruncが提供されていないことがあります。

その場合、自前で似たような動作を実装することができます。

truncは0方向への丸めなので、符号によってfloorとceilを使い分けることでエミュレートできます。

C言語
#include <stdio.h>
#include <math.h>

/*
 * C99以前などで trunc がない場合の簡易実装例
 * 0方向への丸め:
 *   x >= 0 のとき floor(x)
 *   x <  0 のとき ceil(x)
 */
double my_trunc(double x) {
    if (x >= 0.0) {
        return floor(x);
    } else {
        return ceil(x);
    }
}

int main(void) {
    double values[] = { 3.9, 3.1, 0.0, -0.1, -3.1, -3.9 };
    int i;

    for (i = 0; i < 6; i++) {
        double x = values[i];
        printf("x = %5.1f, my_trunc(x) = %5.1f\n", x, my_trunc(x));
    }

    return 0;
}
実行結果
x =   3.9, my_trunc(x) =   3.0
x =   3.1, my_trunc(x) =   3.0
x =   0.0, my_trunc(x) =   0.0
x =  -0.1, my_trunc(x) =   0.0
x =  -3.1, my_trunc(x) =  -3.0
x =  -3.9, my_trunc(x) =  -3.0

−0.1が0.0になるところにも注目すると、truncの「0方向への丸め」の性質がよくわかります。

環境によってはfloorやceilすら存在しない場合もありますが、その場合はキャストや自前のルックアップなど、用途に応じて検討する必要があります。

floor関数や型変換との比較と選び方

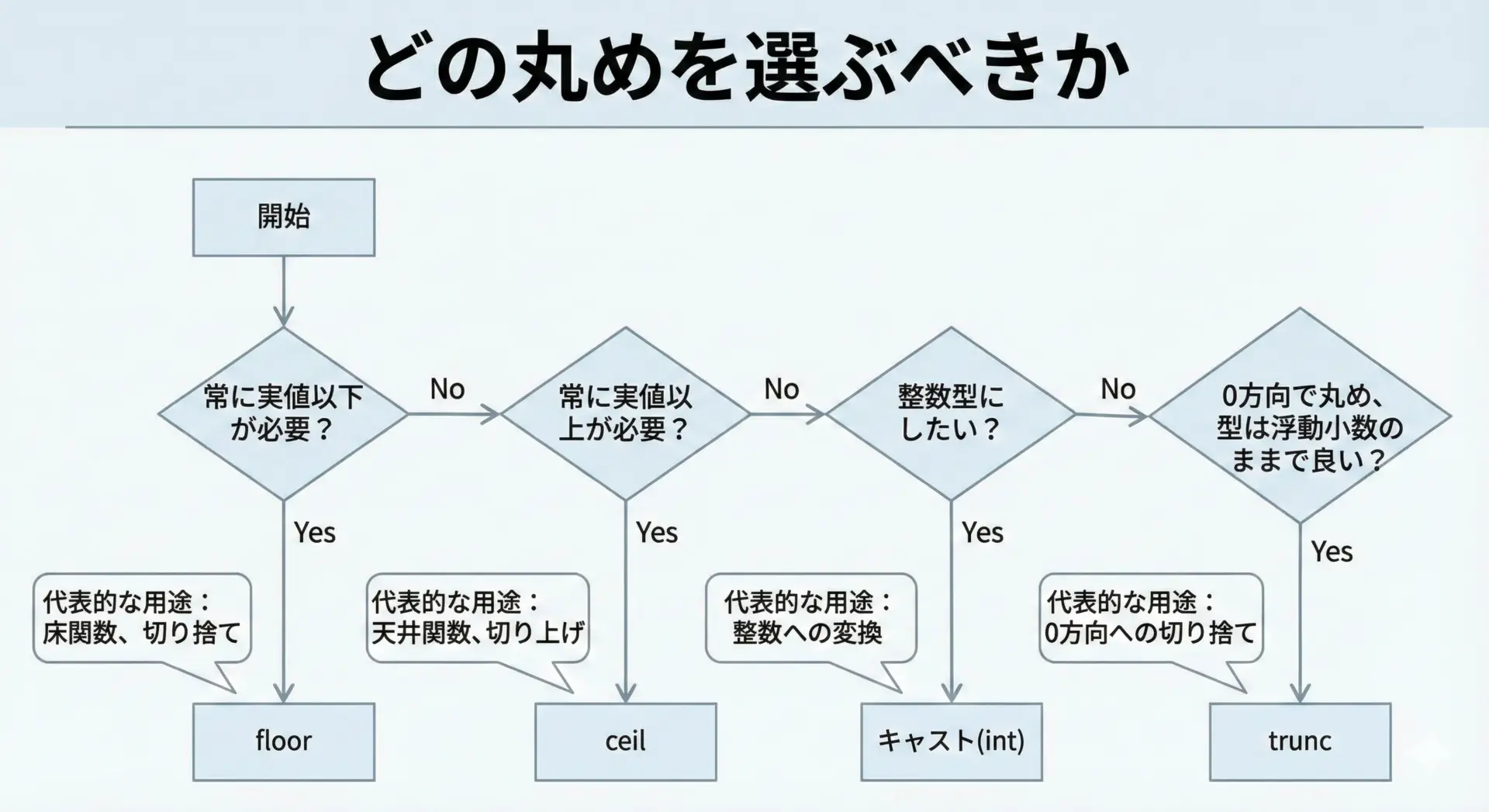
最後に、trunc・floor・ceil・キャストの使い分けの視点を整理します。

  1. 「実際の値を超えない」結果が必須な場合
    代表例: 必ず「安全側」に見積もる在庫数
    →floorを使う(常に小さい方向へ)
  2. 「実際の値より小さくならない」ことが必須な場合
    代表例: 必要な箱数・ページ数など上限側の見積もり
    →ceilを使う(常に大きい方向へ)
  3. 整数型として扱いたい場合
    代表例: 配列添字、ループ回数など
    →(int)xなどのキャスト(0方向丸め)
    ※オーバーフローに注意
  4. 0方向の丸めを行いたいが、結果は浮動小数点で扱いたい場合
    代表例: 後続も浮動小数演算を続けるが、小数以下を切り捨てたい
    →truncを使う

「切り捨て」という日本語だけでは、floorとtrunc、キャストがごちゃ混ぜになりやすいため、必ず「どの方向へ丸めるか」「型はどうしたいか」という2つの軸で判断すると安全です。

まとめ

trunc関数は、「0方向への丸め」つまり小数部だけを単純に捨て、絶対値を小さくする浮動小数点用の関数です。

floor・ceil・roundとの違い、キャストとの関係を押さえておくことで、負の値を扱う場合でも意図通りの結果を得られます。

特に、負の値での挙動と整数型へのキャスト時のオーバーフローには注意が必要です。

C99以降であればmath.hからtrunc系関数を利用でき、C99以前の環境でもfloorとceilを組み合わせて代替実装が可能です。

用途ごとに「丸め方向」と「結果の型」という2つの観点から最適な関数を選び、小数の切り捨て処理を安全かつ分かりやすく実装していきましょう。

数学・数値処理

クラウドSSLサイトシールは安心の証です。

URLをコピーしました！