C言語のroundで四捨五入をわかりやすく｜0.5と負数の正しい扱い方

2025年10月27日2026年1月14日

C言語

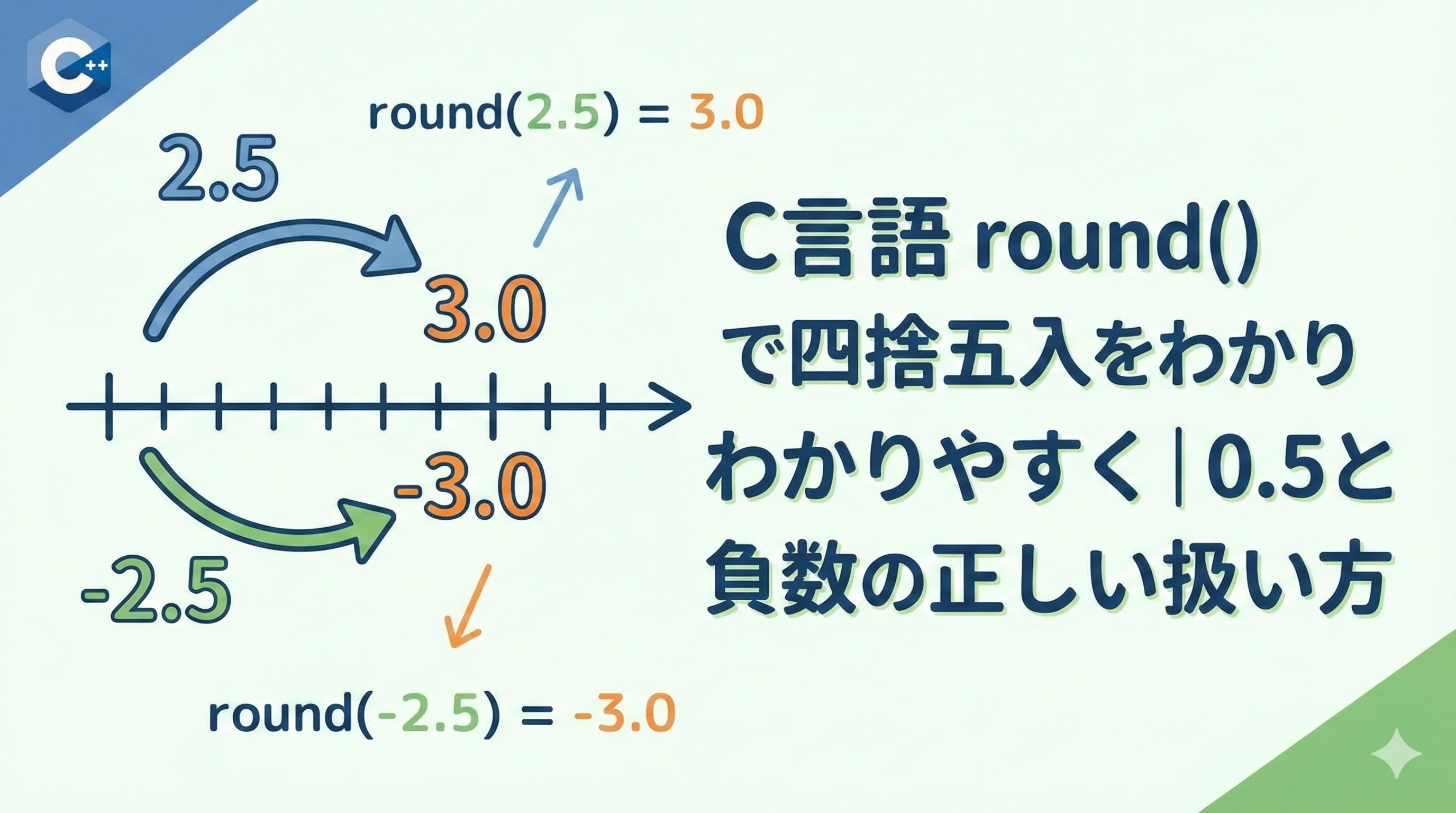
C言語で小数を四捨五入するとき、round関数を正しく理解して使えるかどうかで、計算結果の信頼性が大きく変わります。

とくに0.5の扱いや負の数の丸め方は勘違いしやすいポイントです。

この記事では、round関数の基本から、0.5や負数の正しい丸めルール、浮動小数点誤差への注意点まで、実行例とコードを交えながら丁寧に解説します。

目次 [ close ]

round関数とは

roundとは

round関数は、浮動小数点数を「最も近い整数値」に丸めて返す関数です。

C言語の標準ライブラリで定義されており、主に以下のような用途で利用されます。

小数の計算結果を四捨五入して表示したいとき
金額や個数など、本来は整数で扱う値を丸めたいとき
グラフ表示や統計処理などで、見やすい整数に変換したいとき

ただし、「四捨五入」といっても、学校で習うイメージそのままではない部分があります。

特に0.5の扱いと負の数の丸めは、round独自のルールになっていますので、後ほど詳しく説明します。

roundが定義されているヘッダファイル

round関数は、C99以降で追加された数学関数の1つです。

そのため、使用するには#include <math.h>が必要です。

また、コンパイル時に数学ライブラリをリンクするために、GCCなどでは-lmオプションが必要になる場合があります。

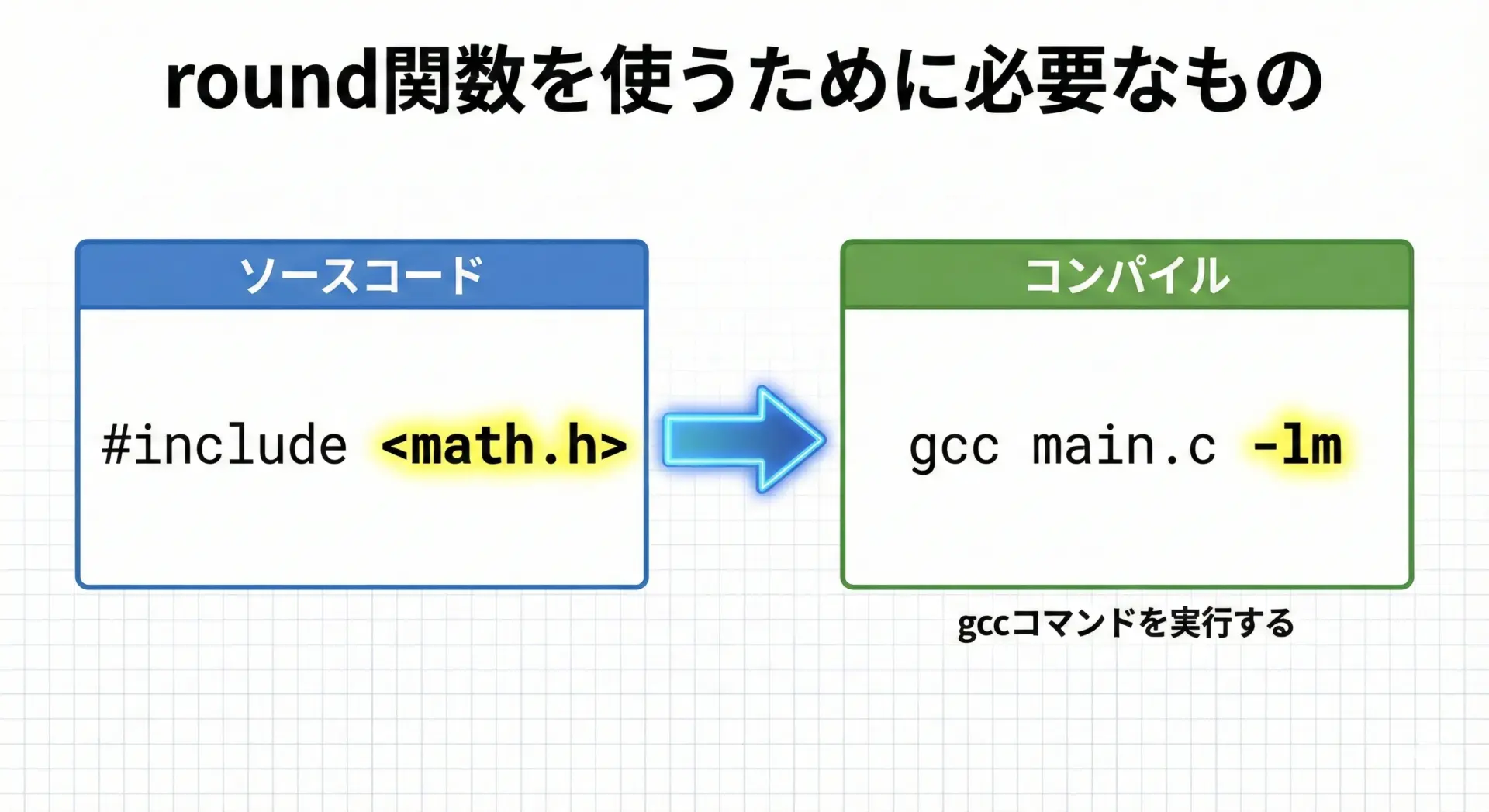
math.hのインクルードとコンパイルの例

C言語

// round関数の利用例 (コンパイル時に -lm が必要な環境が多いです)
#include <stdio.h>
#include <math.h>

int main(void) {
    double x = 3.6;
    double r = round(x);  // 3.6 を最も近い整数に丸める

    printf("x = %.1f, round(x) = %.1f\n", x, r);
    return 0;
}

実行結果

x = 3.6, round(x) = 4.0

環境によっては、コンパイルコマンドをgcc main.c -lmのように指定する必要があります。

roundの基本的な書式と戻り値の型

roundには、扱う型に応じていくつかのバリエーションがあります。

代表的なものを表にまとめます。

関数名	引数の型	戻り値の型	ヘッダ
round	double	double	math.h
roundf	float	float	math.h
roundl	long double	long double	math.h

基本形の書式は次のようになります。

C言語

double round(double x);
float  roundf(float x);
long double roundl(long double x);

「最も近い整数」ではありますが、戻り値の型は整数ではなく浮動小数点型です。

整数として利用したい場合は、戻り値をintなどにキャストします。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double x = 2.7;

    double rd = round(x);       // double型のまま
    int    ri = (int)round(x);  // 整数にキャストして利用

    printf("round(%.1f) as double = %.1f\n", x, rd);
    printf("round(%.1f) as int    = %d\n",   x, ri);
    return 0;
}

実行結果

round(2.7) as double = 3.0
round(2.7) as int    = 3

roundで四捨五入する基本

正の値をroundで四捨五入する例

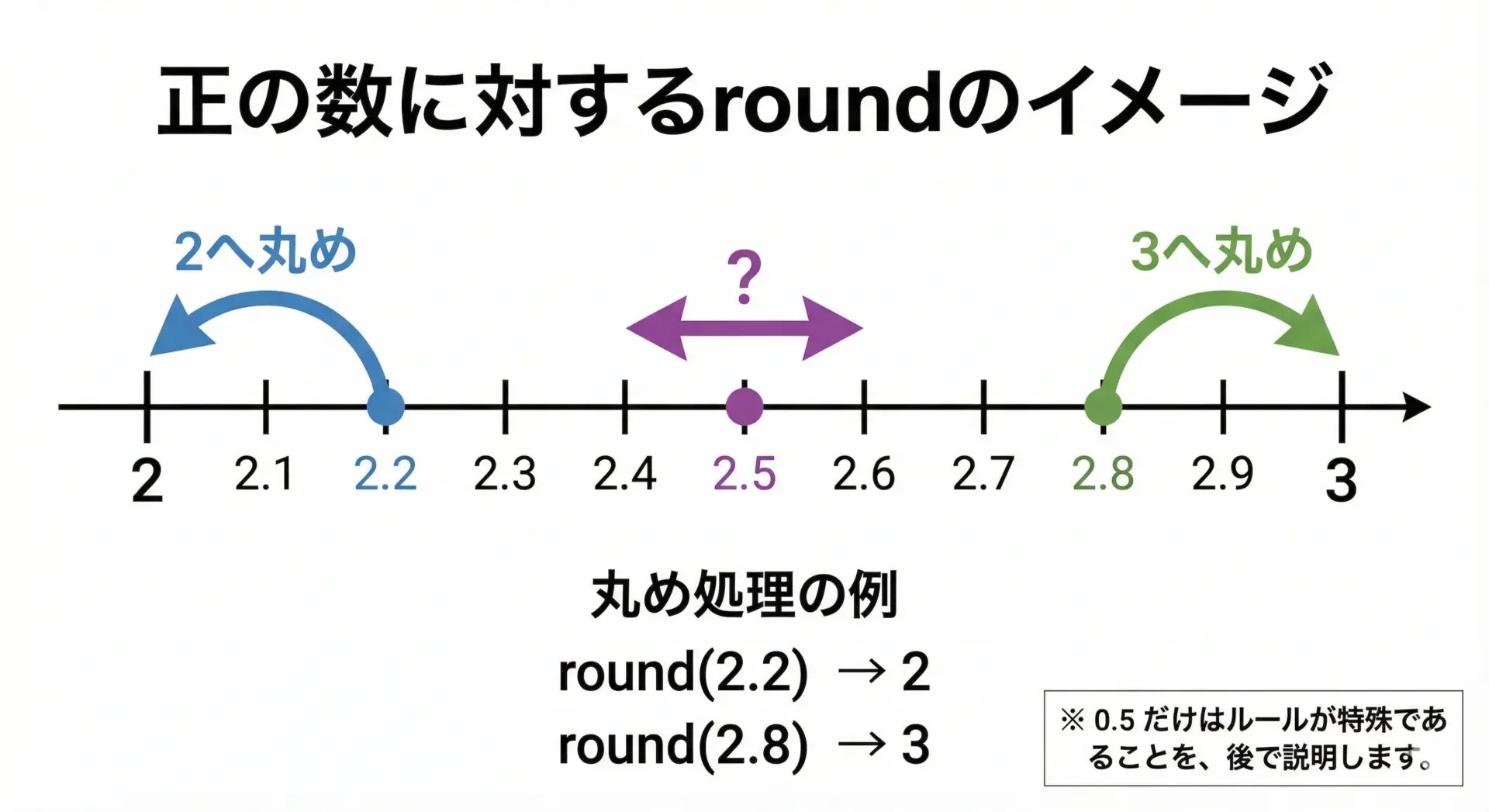
roundの基本的なイメージは、「最も近い整数へ丸める」というものです。

まずは、0.5ちょうどではない正の数をいくつか試してみます。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { 1.2, 1.4, 1.6, 1.8, 2.3, 2.7 };
    int n = sizeof(values) / sizeof(values[0]);

    for (int i = 0; i < n; i++) {
        double x = values[i];
        double r = round(x);  // 最も近い整数に丸める
        printf("round(%.1f) = %.1f\n", x, r);
    }

    return 0;
}

実行結果

round(1.2) = 1.0
round(1.4) = 1.0
round(1.6) = 2.0
round(1.8) = 2.0
round(2.3) = 2.0
round(2.7) = 3.0

この結果から、0.5ではない場合は通常の「四捨五入」のイメージと同じ動作をしていることがわかります。

すなわち、0.5より小さい端数は切り捨て、0.5より大きい端数は切り上げられます。

小数第1位・第2位でroundを使った四捨五入

round関数は小数第0位(整数部分)に対する丸めを行いますが、少し工夫すれば小数第1位や第2位での四捨五入も可能です。

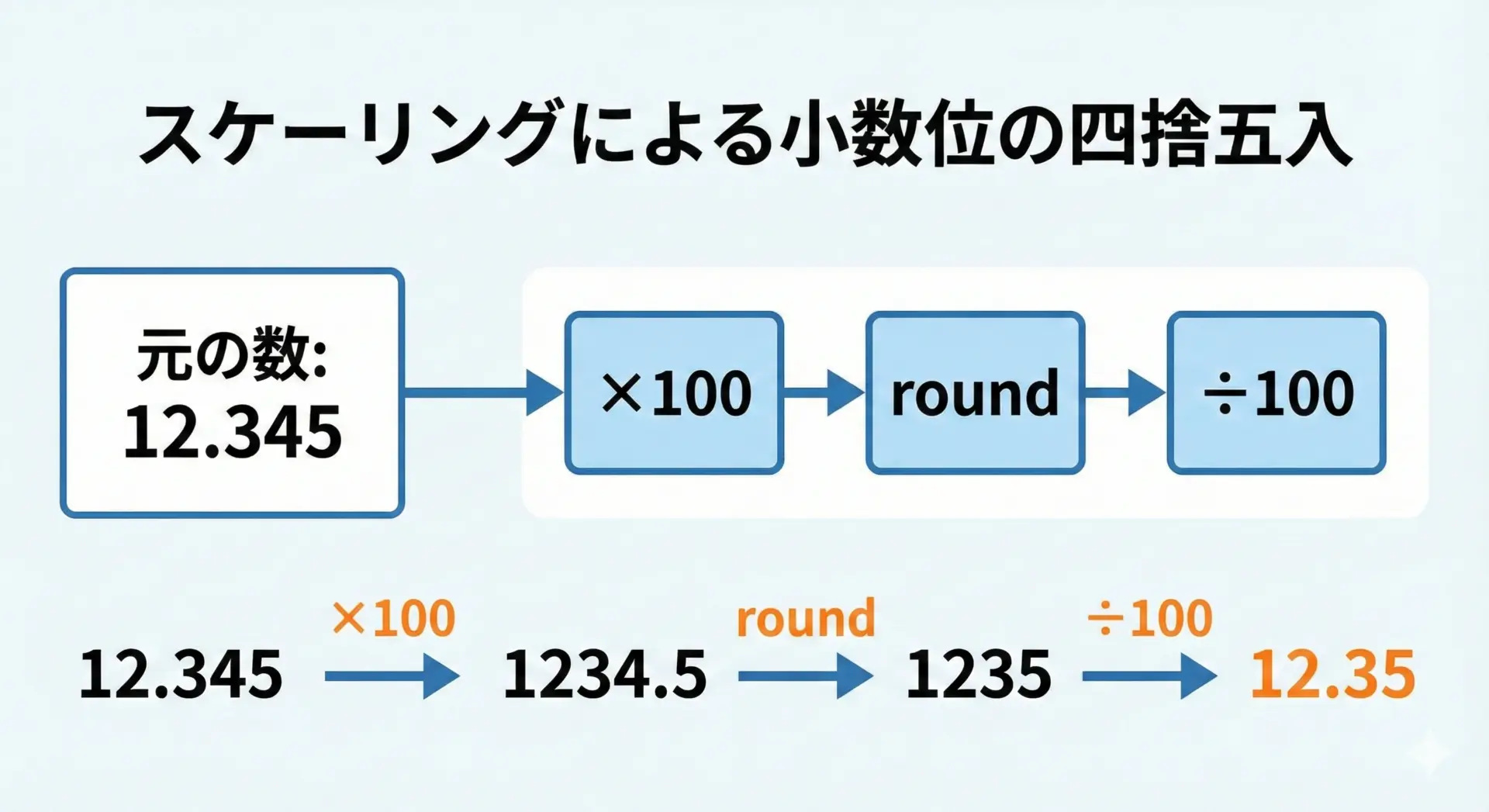
小数第1位(1桁目)で四捨五入する例

小数第1位で四捨五入して小数第1位まで残すには、10倍 → round → 10で割るという手順を使います。

C言語

#include <stdio.h>
#include <math.h>

// 小数第1位で四捨五入して、小数第1位まで残す関数
double round1(double x) {
    return round(x * 10.0) / 10.0;
}

// 小数第2位で四捨五入して、小数第2位まで残す関数
double round2(double x) {
    return round(x * 100.0) / 100.0;
}

int main(void) {
    double x = 12.345;

    double r1 = round1(x);  // 小数第1位で四捨五入
    double r2 = round2(x);  // 小数第2位で四捨五入

    printf("元の値      : %.5f\n", x);
    printf("小数第1位で : %.1f\n",  r1);
    printf("小数第2位で : %.2f\n",  r2);

    return 0;
}

実行結果

元の値      : 12.34500
小数第1位で : 12.3
小数第2位で : 12.35

このように、丸めたい桁数だけ10のべき乗でスケーリングしてからroundをかけることで、任意の桁での四捨五入が実現できます。

キャスト(int)との違い

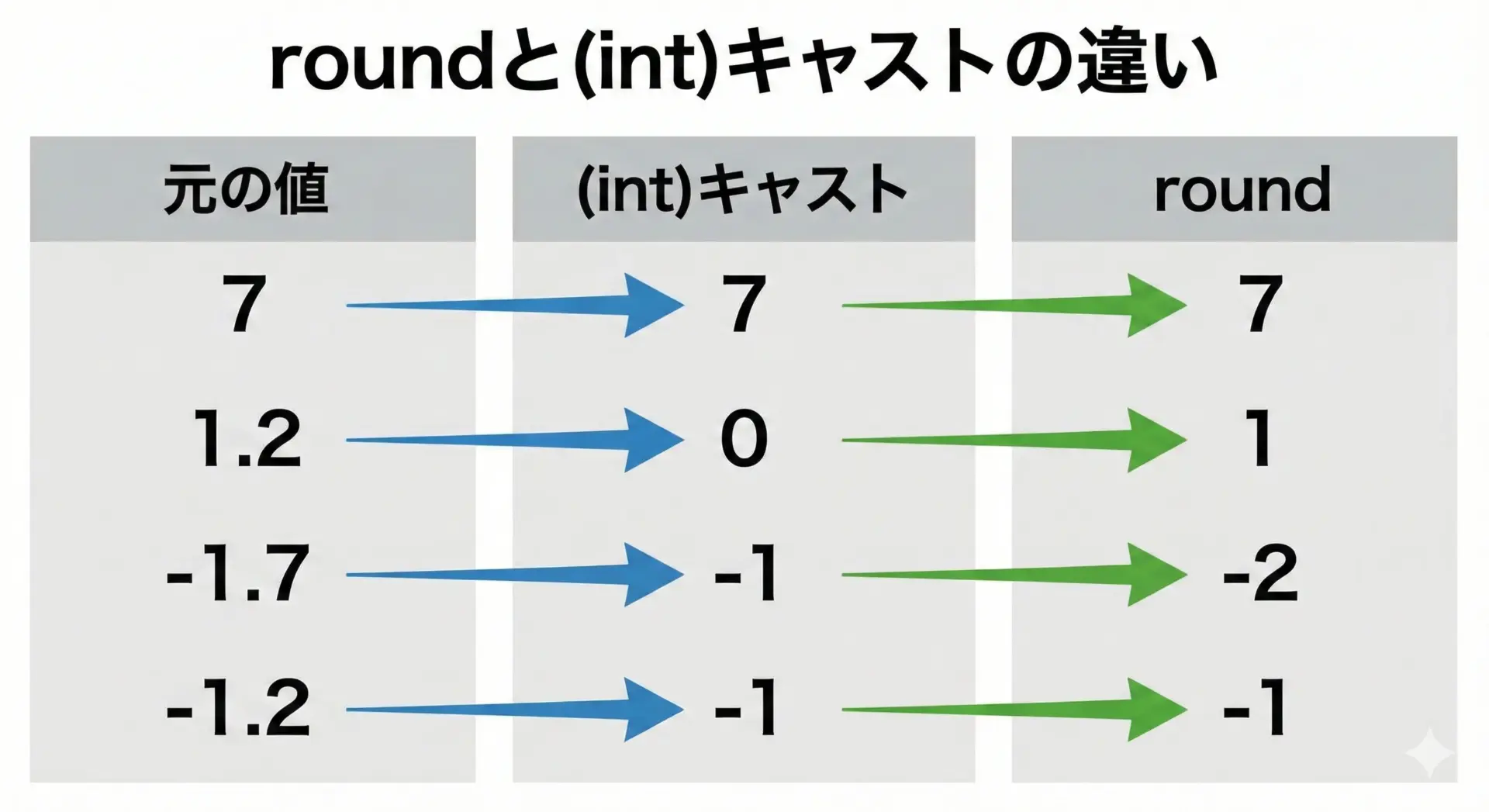
C言語では、(int)xのようにキャストすることで、小数を整数に変換できます。

しかし、キャストは「丸め」ではなく「切り捨て」である点に注意が必要です。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { 2.7, 2.2, -2.7, -2.2 };
    int n = sizeof(values) / sizeof(values[0]);

    for (int i = 0; i < n; i++) {
        double x = values[i];
        int ci = (int)x;       // 単純なキャスト(小数部分を切り捨て)
        int ri = (int)round(x); // roundしてからintに変換

        printf("x = %4.1f, (int)x = %3d, (int)round(x) = %3d\n", x, ci, ri);
    }

    return 0;
}

実行結果

x =  2.7, (int)x =   2, (int)round(x) =   3
x =  2.2, (int)x =   2, (int)round(x) =   2
x = -2.7, (int)x =  -2, (int)round(x) =  -3
x = -2.2, (int)x =  -2, (int)round(x) =  -2

この例から、(int)キャストは0方向に切り捨てるのに対して、roundは最も近い整数へ丸めることがわかります。

特に負の数では結果が大きく変わるため、用途に応じて使い分けることが重要です。

roundと0.5の扱い

roundにおける0.5の四捨五入ルール

roundが通常の「四捨五入」と大きく異なるのは、端数がちょうど0.5になる場合です。

C言語のround関数は、「0.5は常に切り上げる」わけではありません。

C標準では、roundの丸め方を「0.5は無限大方向に丸める」と定義しています。

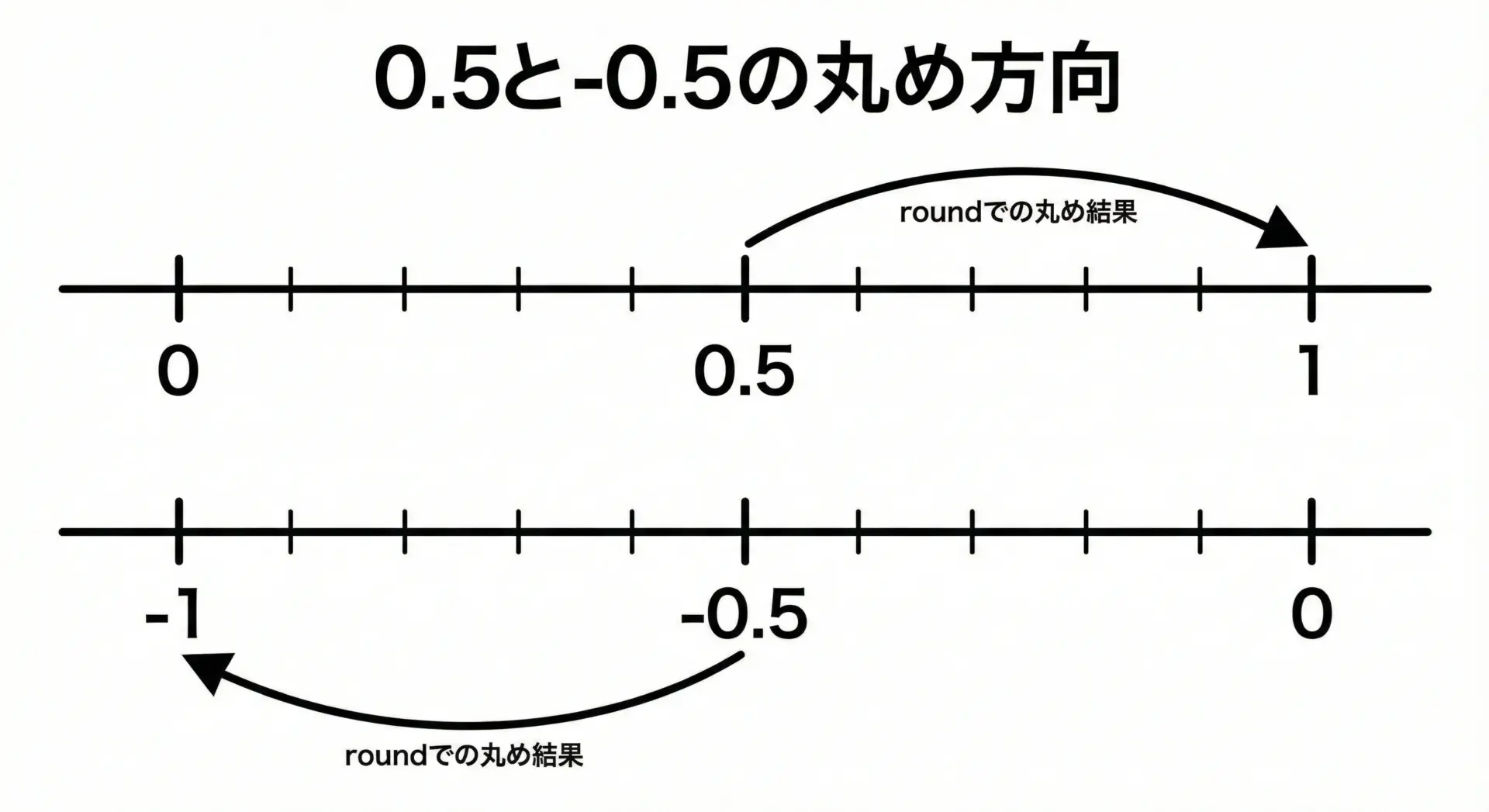
より平易に言えば、正の数の0.5は大きい方(正の無限大方向)、負の数の-0.5は小さい方(負の無限大方向)に丸めるというルールです。

この性質は+∞方向への丸めを行うceilや、-∞方向への丸めを行うfloorと関連がありますが、roundでは「最も近い整数」の条件があるため、0.5以外では通常の四捨五入と同じように働きます。

0.5はどちらに丸められるか

正の0.5と負の-0.5について、実際にroundを呼び出して確認してみます。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double a = 0.5;
    double b = 1.5;
    double c = -0.5;
    double d = -1.5;

    printf("round( %.1f) = %.1f\n", a, round(a));
    printf("round( %.1f) = %.1f\n", b, round(b));
    printf("round(%.1f) = %.1f\n", c, round(c));
    printf("round(%.1f) = %.1f\n", d, round(d));

    return 0;
}

実行結果

round( 0.5) = 1.0
round( 1.5) = 2.0
round(-0.5) = -1.0
round(-1.5) = -2.0

この結果から、0.5は「常に大きい方の整数に丸められる」ことがわかります。

5 → 1.0
5 → 2.0
-0.5 → -1.0
-1.5 → -2.0

学校の「四捨五入」は、通常は0.5を常に絶対値の大きい方向に丸めるとは限りませんが、Cのroundは無限大方向へ丸めるという、一貫した定義になっています。

浮動小数点誤差と0.5をroundするときの注意点

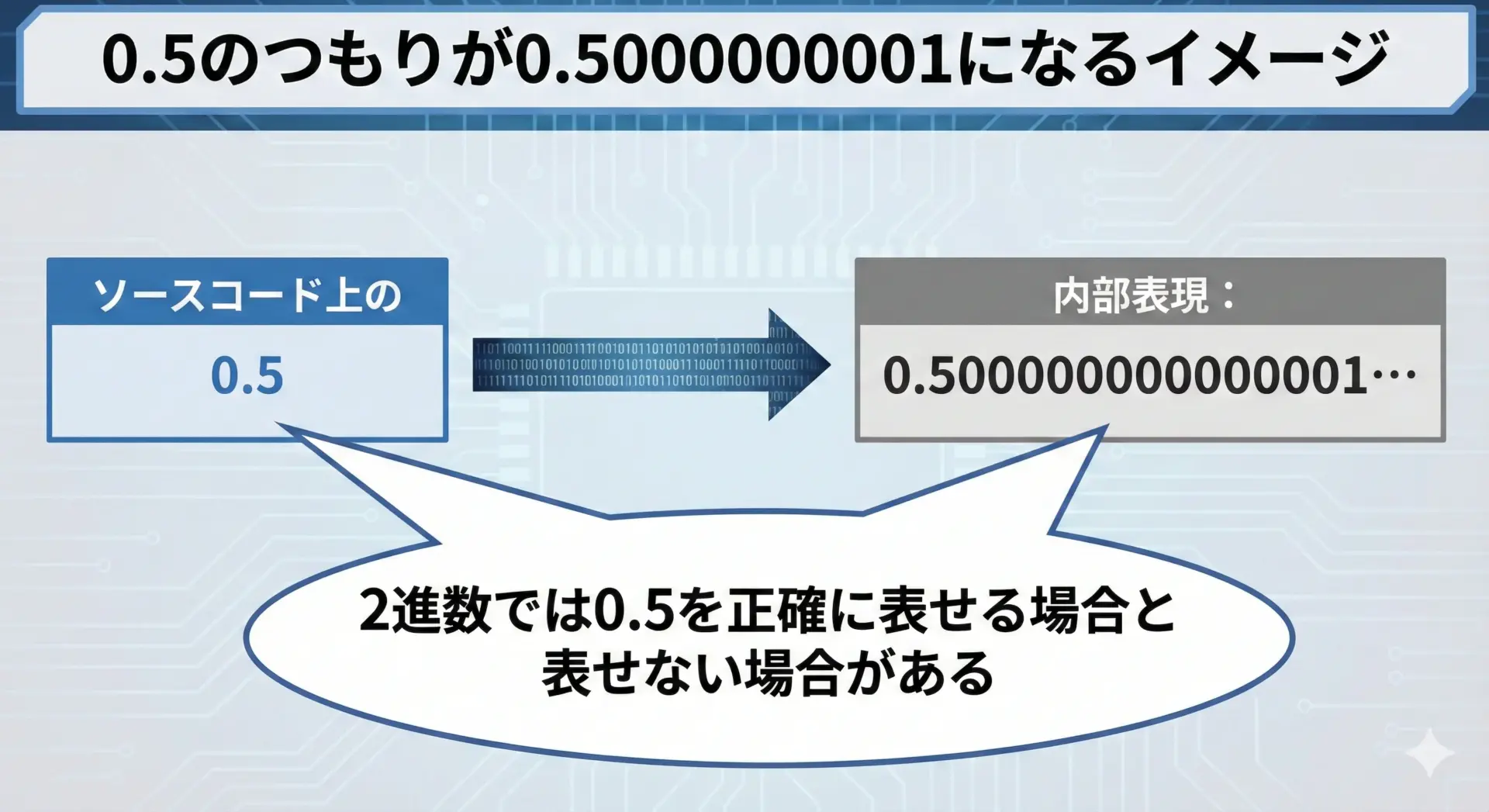
0.5の扱いを理解していても、実際のプログラムでは「0.5のつもりなのに、roundの結果が想定外になる」ということが起きます。

その主な原因は浮動小数点誤差です。

0.5にならない「0.1の合計」問題

典型的な例として、0.1を何回か足して0.5にしたつもりが、内部的にはわずかにズレた値になってしまうケースがあります。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double x = 0.1 * 5;  // 0.5になってほしい値

    printf("x = %.17f\n", x);
    printf("round(x) = %.1f\n", round(x));

    return 0;
}

実行結果

x = 0.50000000000000000   ← 環境によっては 0.49999999999999994 などと表示されることがあります
round(x) = 1.0

環境によってはxが0.49999999999999994のように表示される場合があり、その場合は「0.5未満」とみなされて0に丸められる可能性もあります。

誤差を意識した対策

このような誤差を完全に避けることは困難ですが、次のような工夫で実務上のトラブルを減らせます。

元データを整数で管理し、表示時だけスケーリングして小数を扱う
金額など、誤差が問題になる値はintやlong longで「1円=1」「1銭=1」などと決めて扱う
「0.1を何回か足して0.5にする」といった計算は避け、0.5を直接使う

roundは正しく動いていても、入力値がすでに誤差を含んでいるという前提を意識して設計することが大切です。

roundと負の数の丸め

roundで負の数を四捨五入するルール

roundは、正の数と同様に、負の数でも「最も近い整数」に丸めます。

ただし、前のセクションで説明した通り、端数がちょうど0.5のときは無限大方向(正なら上、負なら下)に丸めるという点が特徴的です。

0.5以外の端数については、次のような挙動になります。

-1.2 → -1.0 (0に近い方)
-1.6 → -2.0 (より小さい方)

つまり、0.5ちょうど「以外」は、通常の四捨五入の感覚と同じです。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { -1.2, -1.4, -1.6, -1.8, -2.3, -2.7 };
    int n = sizeof(values) / sizeof(values[0]);

    for (int i = 0; i < n; i++) {
        double x = values[i];
        printf("round(%4.1f) = %4.1f\n", x, round(x));
    }

    return 0;
}

実行結果

round(-1.2) = -1.0
round(-1.4) = -1.0
round(-1.6) = -2.0
round(-1.8) = -2.0
round(-2.3) = -2.0
round(-2.7) = -3.0

-0.5や-1.5はどう丸められるか

負の数で特に混乱しやすいのが、-0.5や-1.5など「端数0.5」を含む値です。

先ほども触れましたが、roundは端数0.5のときは常に無限大方向(ここでは負方向)に丸めます。

実際のコードで確認してみます。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { -0.5, -1.5, -2.5, -3.5 };
    int n = sizeof(values) / sizeof(values[0]);

    for (int i = 0; i < n; i++) {
        double x = values[i];
        printf("round(%4.1f) = %4.1f\n", x, round(x));
    }

    return 0;
}

実行結果

round(-0.5) = -1.0
round(-1.5) = -2.0
round(-2.5) = -3.0
round(-3.5) = -4.0

結果からわかるように、-0.5, -1.5, -2.5, … はすべて、より小さい整数に丸められます。

これは、floor(-0.5) = -1の動作と一致しているようにも見えますが、roundが常にfloorと同じになるわけではありません。

負数でのroundとfloor・ceilとの違い

負の数を丸める関数としては、roundの他にfloorとceilがあります。

それぞれの動作は次の通りです。

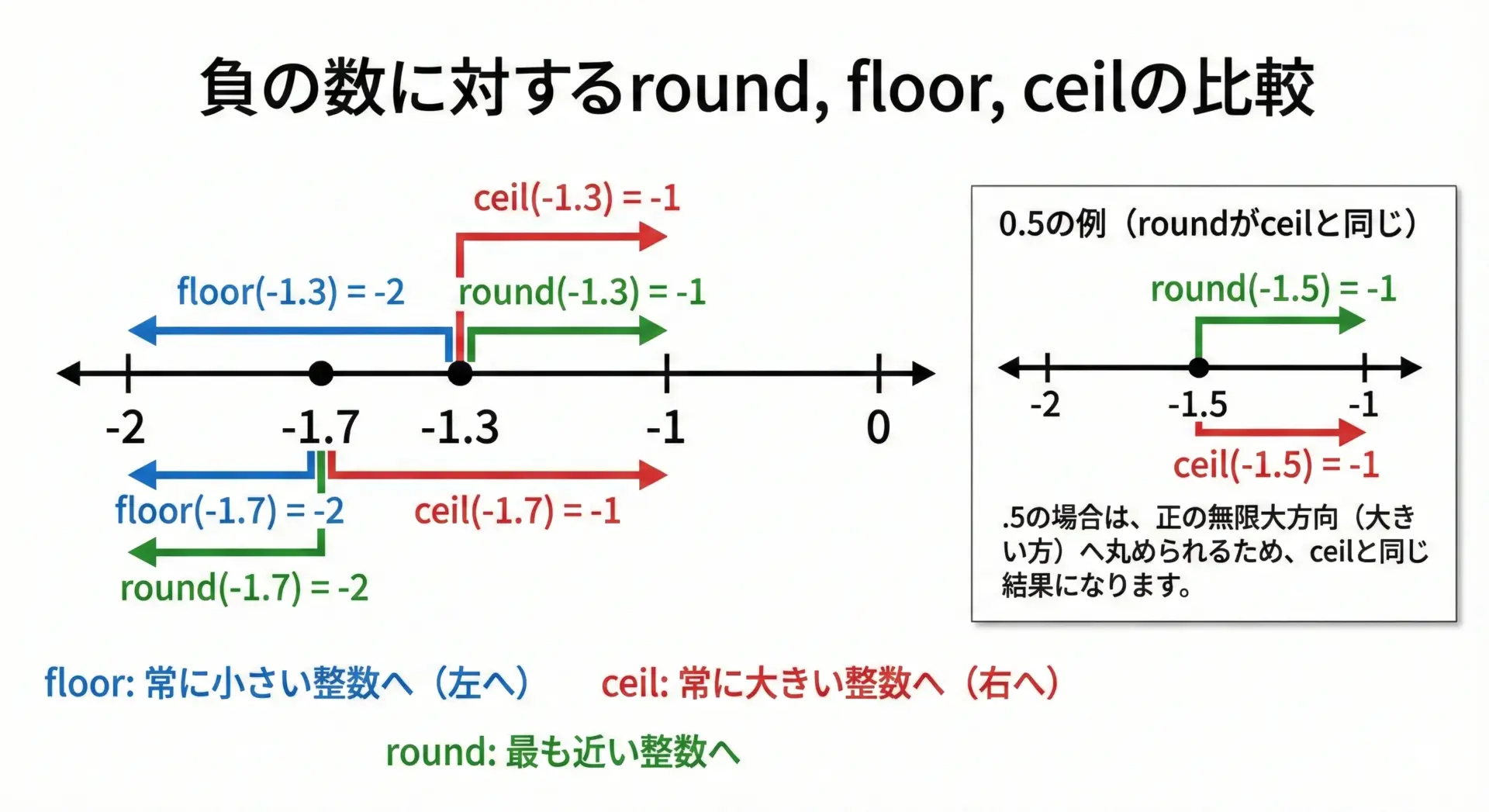
floor(x): xを負の無限大方向(切り下げ)に丸める
ceil(x): xを正の無限大方向(切り上げ)に丸める
round(x): xを最も近い整数に丸める(端数0.5は無限大方向)

動作比較のコード例

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double values[] = { -2.7, -2.5, -2.3, -1.7, -1.5, -1.3 };
    int n = sizeof(values) / sizeof(values[0]);

    printf("   x    floor   ceil  round\n");
    printf("-----------------------------\n");

    for (int i = 0; i < n; i++) {
        double x = values[i];
        printf("%5.1f %6.1f %6.1f %6.1f\n",
               x, floor(x), ceil(x), round(x));
    }

    return 0;
}

実行結果

   x    floor   ceil  round
-----------------------------
 -2.7   -3.0   -2.0   -3.0
 -2.5   -3.0   -2.0   -3.0
 -2.3   -3.0   -2.0   -2.0
 -1.7   -2.0   -1.0   -2.0
 -1.5   -2.0   -1.0   -2.0
 -1.3   -2.0   -1.0   -1.0

この表を見ると、次のような関係があることがわかります。

1. floorは常に「小さい方」の整数に丸める 2. ceilは常に「大きい方」の整数に丸める 3. roundは最も近い整数に丸めるが、端数0.5のときだけceilと同じ方向(無限大方向)に丸める

つまり、「負の数で0.5がつく値」だけは、roundがfloorのようにもceilのようにも見え、そのために混乱が生じやすいのです。

実務では、次のように使い分けるとよいでしょう。

四捨五入がしたい → round
常に少なめに見積もりたい(在庫、リスク評価など) → floor
常に多めに見積もりたい(必要量、予算など) → ceil

まとめ

round関数は、「最も近い整数に丸める」ための標準関数であり、正しい使い方を理解しておくことで、小数計算の信頼性を高めることができます。

特に重要なのは、0.5は常に無限大方向へ丸められること、そして負の数でも同じルールが適用されるという点です。

また、浮動小数点誤差により「0.5のつもり」が0.5ではない値になることもあるため、整数での管理やスケーリングなどの工夫も欠かせません。

用途に応じてround、floor、ceil、キャストを適切に選び、意図どおりの丸めを行えるようにしておきましょう。