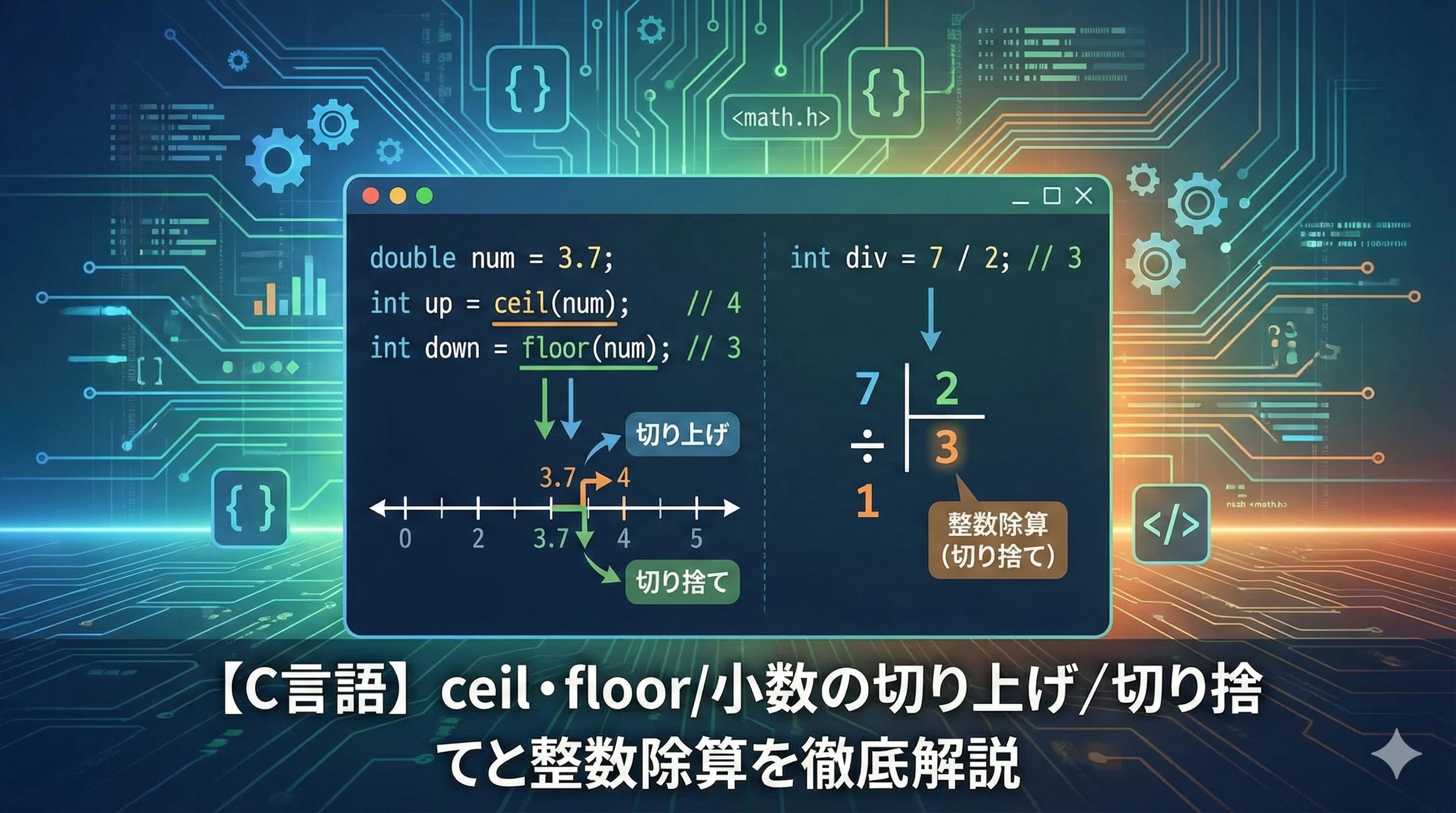
C言語では、小数の切り上げ(ceil)や切り捨て(floor)を正しく扱うことが、金額計算やページ数計算などでとても重要になります。
また、整数同士の割り算は、自動的に小数点以下が切り捨てられるため、その挙動を理解していないとバグの原因になります。
本記事では、ceil・floor関数と整数除算の基本から、実務で役立つ実装パターンまで、図解とコード例を交えて詳しく解説します。
ceil・floorと整数除算の基本
ceilとfloorの役割
まずは、ceilとfloorが数学的にどのような役割を持っているかを整理します。
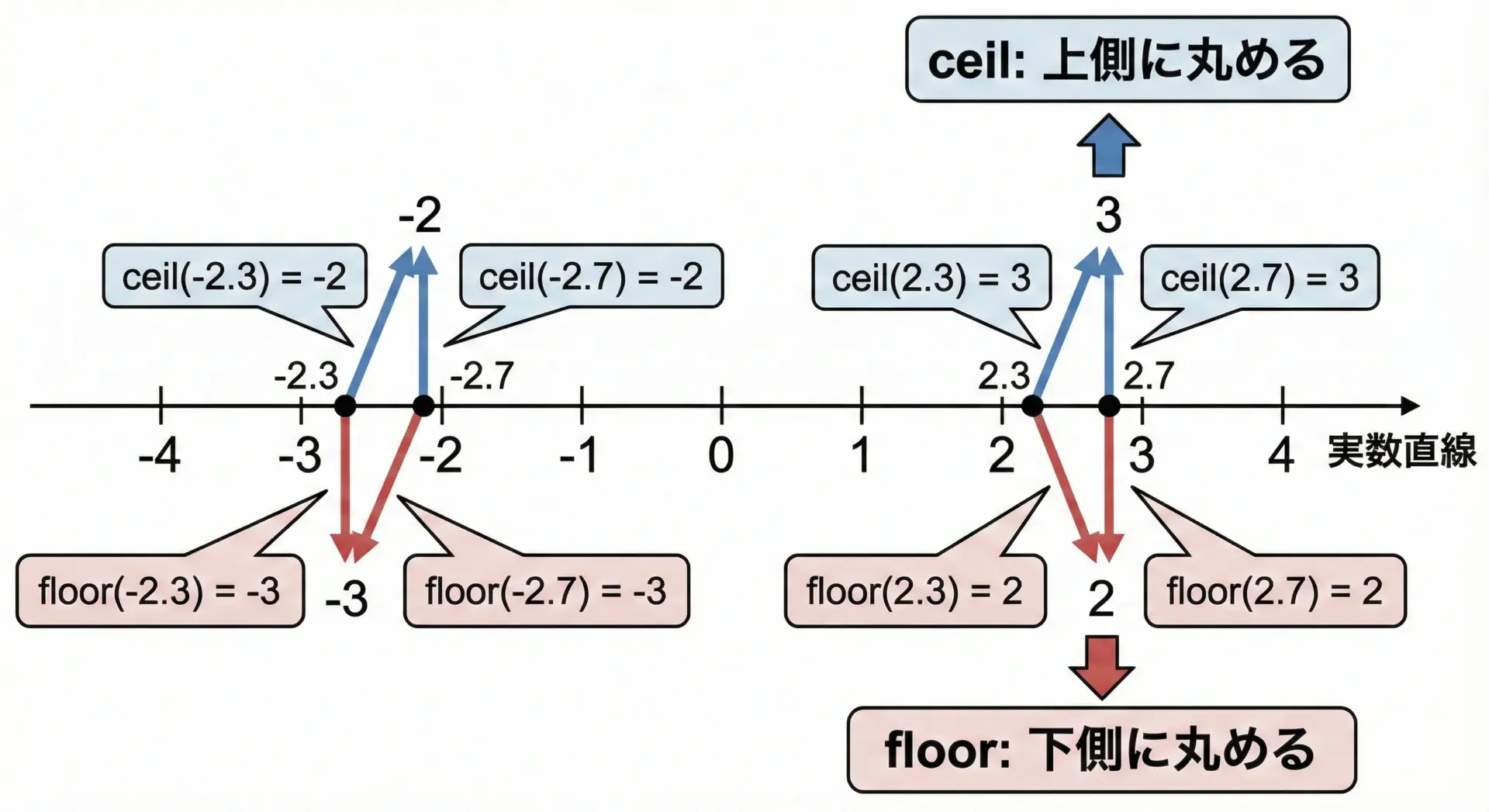
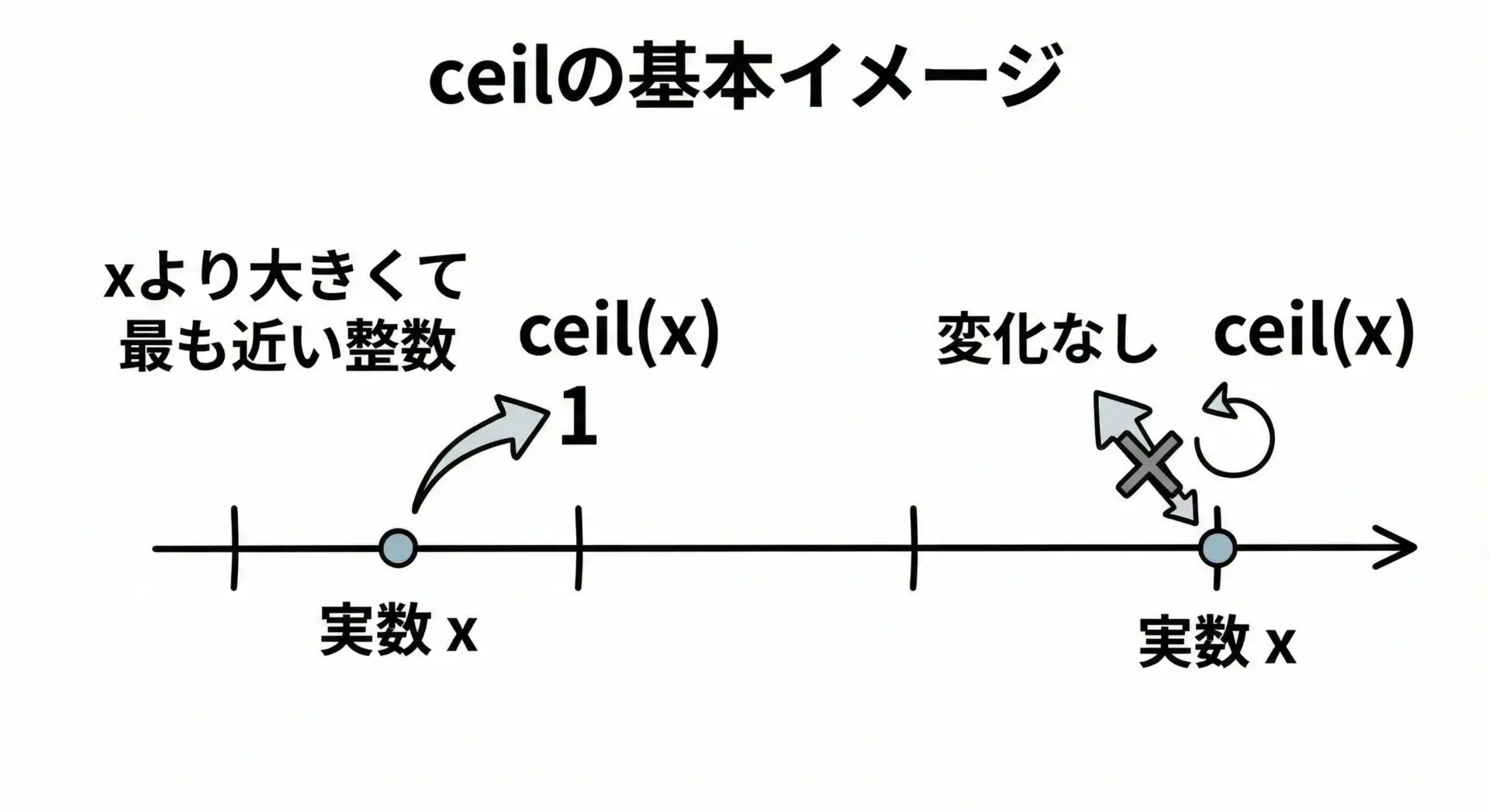
ceilとfloorは、どちらも実数(浮動小数点数)を整数方向に丸める関数ですが、丸める「向き」が異なります。
- ceil(x): 「x以上の最小の整数」を返します
小数点以下を切り上げるイメージです。 - floor(x): 「x以下の最大の整数」を返します
小数点以下を切り捨てるイメージです。
ここで重要なのは、「整数」と言っても戻り値の型は後ほど説明するようにdouble型であることです。
見た目は整数でも、中身は浮動小数点として扱われます。
代表的な例を表にまとめます。
| x | ceil(x) | floor(x) |
|---|---|---|
| 2.3 | 3.0 | 2.0 |
| 2.0 | 2.0 | 2.0 |
| -2.3 | -2.0 | -3.0 |
| -2.0 | -2.0 | -2.0 |
負の数での挙動が特に重要です。
たとえば-2.3の場合、ceilは-2.0(0に近い側)、floorは-3.0(0から遠い側)になります。
C言語における整数除算の挙動
次に、C言語で整数同士を割り算した場合の挙動を確認します。
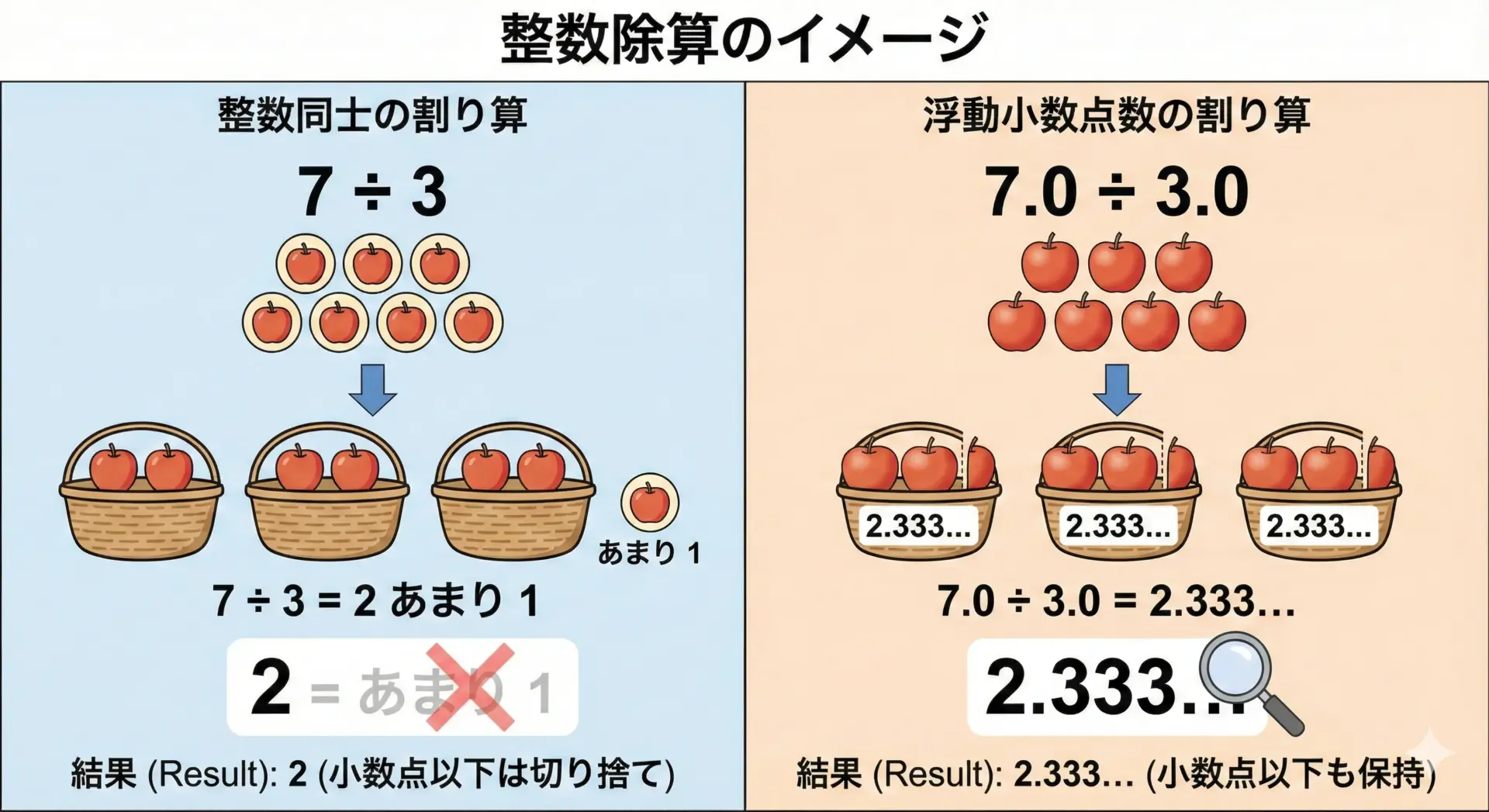
C言語では、次のような場合に整数除算が行われます。
- 被除数(左側)と除数(右側)の両方が整数型(int, long など)のとき
この場合、結果も整数型になり、小数点以下は切り捨てられます。
代表的な例を見てみます。
#include <stdio.h>
int main(void) {
int a = 7;
int b = 3;
int result_int = a / b; // 整数どうしの割り算
double result_double = a / b; // 結果をdoubleに代入しても計算は整数除算
printf("int / int = %d\n", result_int);
printf("int / int (to double) = %f\n", result_double);
return 0;
}int / int = 2
int / int (to double) = 2.000000このように、a / bが計算される時点で、すでに小数点以下が捨てられて2になっているため、その結果をdouble型変数に代入しても2.000000のままです。
小数と整数で結果が変わるケース
整数と小数が混在する場合、どのような結果になるかを整理します。
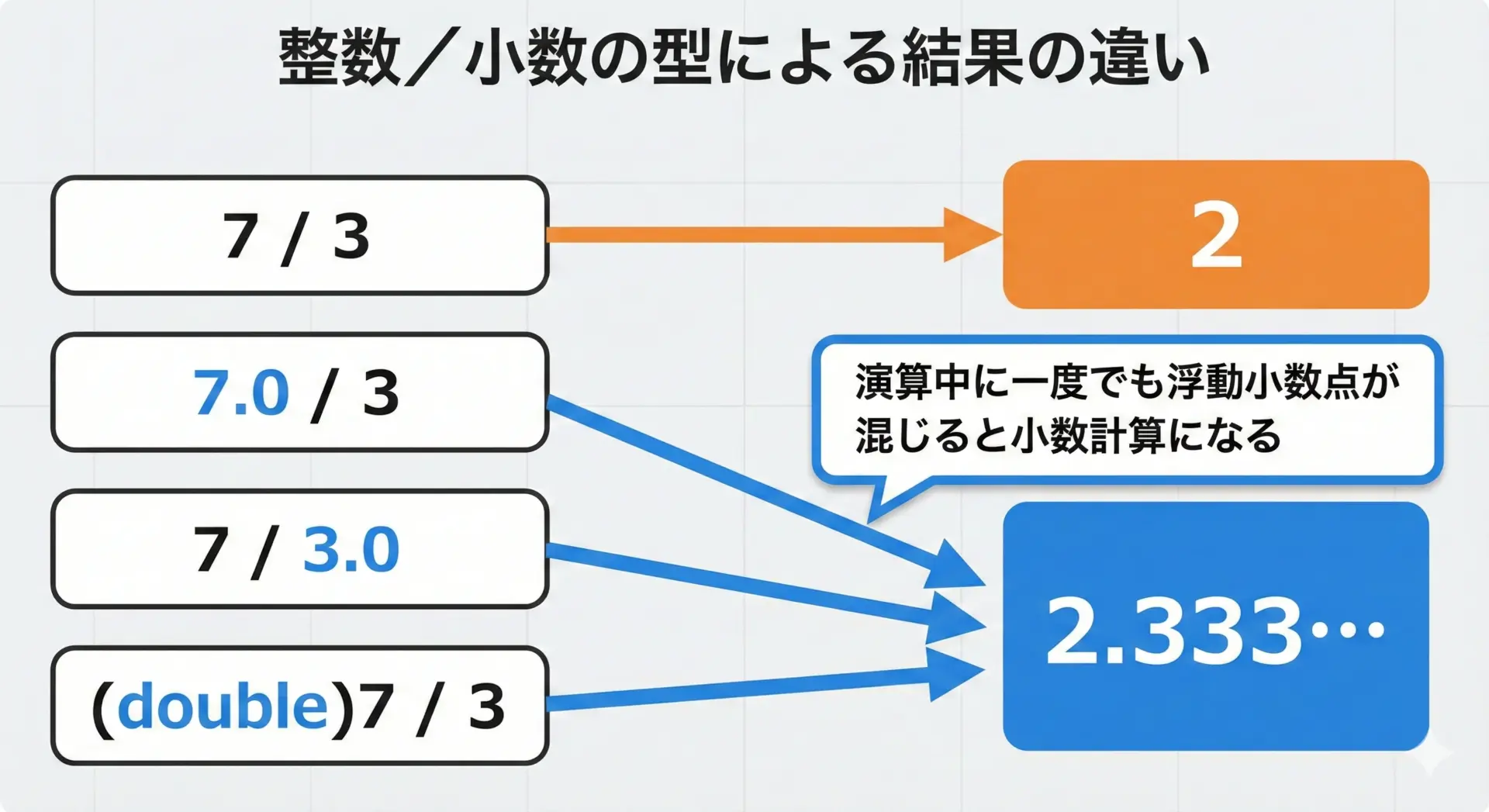
C言語では、演算に参加する値のどれか1つでも浮動小数点型(double, float)であれば、浮動小数点演算になります。
#include <stdio.h>
int main(void) {
int a = 7;
int b = 3;
double d1 = 7.0 / 3; // 左がdouble
double d2 = 7 / 3.0; // 右がdouble
double d3 = (double)a / b; // キャストでdouble
double d4 = a / b; // どちらもint
printf("7.0 / 3 = %f\n", d1);
printf("7 / 3.0 = %f\n", d2);
printf("(double)a / b = %f\n", d3);
printf("a / b = %f (int同士)\n", d4);
return 0;
}7.0 / 3 = 2.333333
7 / 3.0 = 2.333333
(double)a / b = 2.333333
a / b = 2.000000 (int同士)「どのタイミングで浮動小数点になるか」が非常に重要です。
整数同士の割り算のあとでdoubleに代入しても、すでに切り捨てが行われたあとの値しか残っていません。
ceil関数(小数の切り上げ)の使い方
ceilの基本的な使い方と戻り値の型
C言語でceil関数を使うには、math.hをインクルードします。
#include <math.h>ceil関数の宣言は、一般的な環境では次のようになっています。
double ceil(double x);つまり、引数も戻り値もdouble型です。
floatやlong doubleを扱う場合には、次のようなバージョンもあります。
float ceilf(float x);long double ceill(long double x);
基本的な使い方の例を見てみます。
#include <stdio.h>
#include <math.h>
int main(void) {
double x1 = 2.3;
double x2 = 2.0;
double x3 = -2.3;
double r1 = ceil(x1); // 2.3以上の最小の整数 → 3.0
double r2 = ceil(x2); // 2.0以上の最小の整数 → 2.0
double r3 = ceil(x3); // -2.3以上の最小の整数 → -2.0
printf("ceil(2.3) = %.1f\n", r1);
printf("ceil(2.0) = %.1f\n", r2);
printf("ceil(-2.3) = %.1f\n", r3);
return 0;
}ceil(2.3) = 3.0
ceil(2.0) = 2.0
ceil(-2.3) = -2.0ここで注意したいポイントは、戻り値が整数ではなくdoubleであることです。
整数型に代入したい場合は、後で明示的に(int)などのキャストを行う必要があります。
正数・負数でのceilの動作例
ceilの挙動は、特に負の数で混乱しやすいので、正数と負数を並べて確認します。

#include <stdio.h>
#include <math.h>
int main(void) {
double values[] = { 2.1, 2.9, -2.1, -2.9, 0.0 };
int i;
for (i = 0; i < 5; i++) {
double x = values[i];
double r = ceil(x);
printf("x = %5.1f -> ceil(x) = %5.1f\n", x, r);
}
return 0;
}x = 2.1 -> ceil(x) = 3.0
x = 2.9 -> ceil(x) = 3.0
x = -2.1 -> ceil(x) = -2.0
x = -2.9 -> ceil(x) = -2.0
x = 0.0 -> ceil(x) = 0.0ポイントは、「切り上げ」は常に数直線の右側(大きい値)に丸めるということです。
負の数の場合でも、-2.9は-3ではなく-2に丸められます。
ceilを使った端数処理
ceilは、端数が少しでも出たら1つ上の整数にしたい場合に便利です。
例として、次のような用途でよく使われます。
- ページ数の計算(10件ずつ表示、全35件 → 4ページ)
- 必要なバイト数をブロックサイズで切り上げる
- 均等割りで、余りが出たら1つ追加する
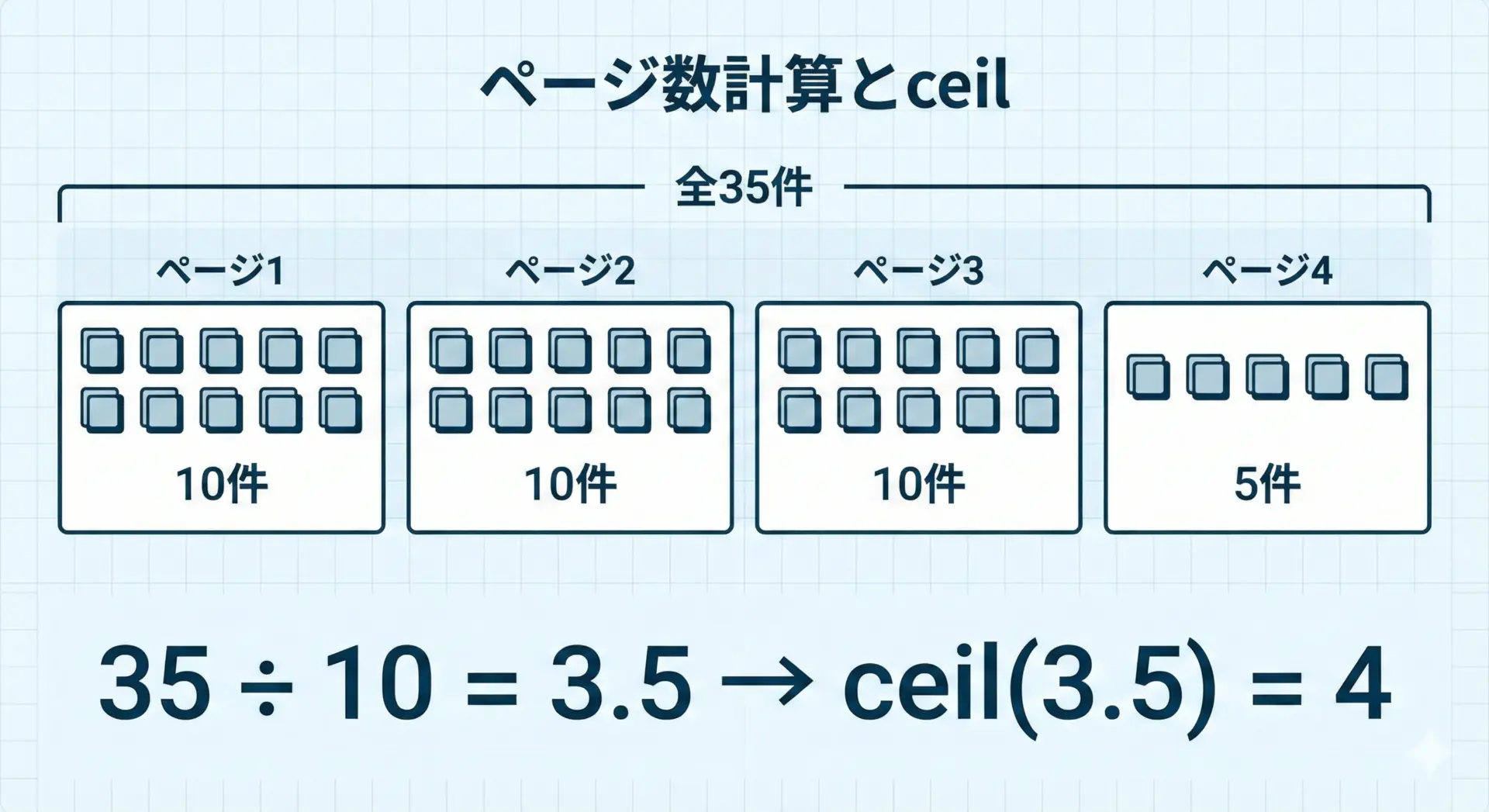
例として、データ件数totalをper_page件ずつ表示するときのページ数を求めてみます。
#include <stdio.h>
#include <math.h>
int main(void) {
int total = 35; // 全件数
int per_page = 10; // 1ページあたりの件数
// まずはdoubleで割り算し、ceilで切り上げたあとintにキャスト
int pages = (int)ceil((double)total / per_page);
printf("total = %d, per_page = %d -> pages = %d\n",
total, per_page, pages);
return 0;
}total = 35, per_page = 10 -> pages = 4注意点として、(double)total / per_pageのように、必ず割り算を浮動小数点演算にしてからceilをかけることが重要です。
整数同士のままでは35 / 10が3になってしまい、ceilをかけても3のままになってしまいます。
floor関数(小数の切り捨て)の使い方
floorの基本的な使い方と戻り値の型
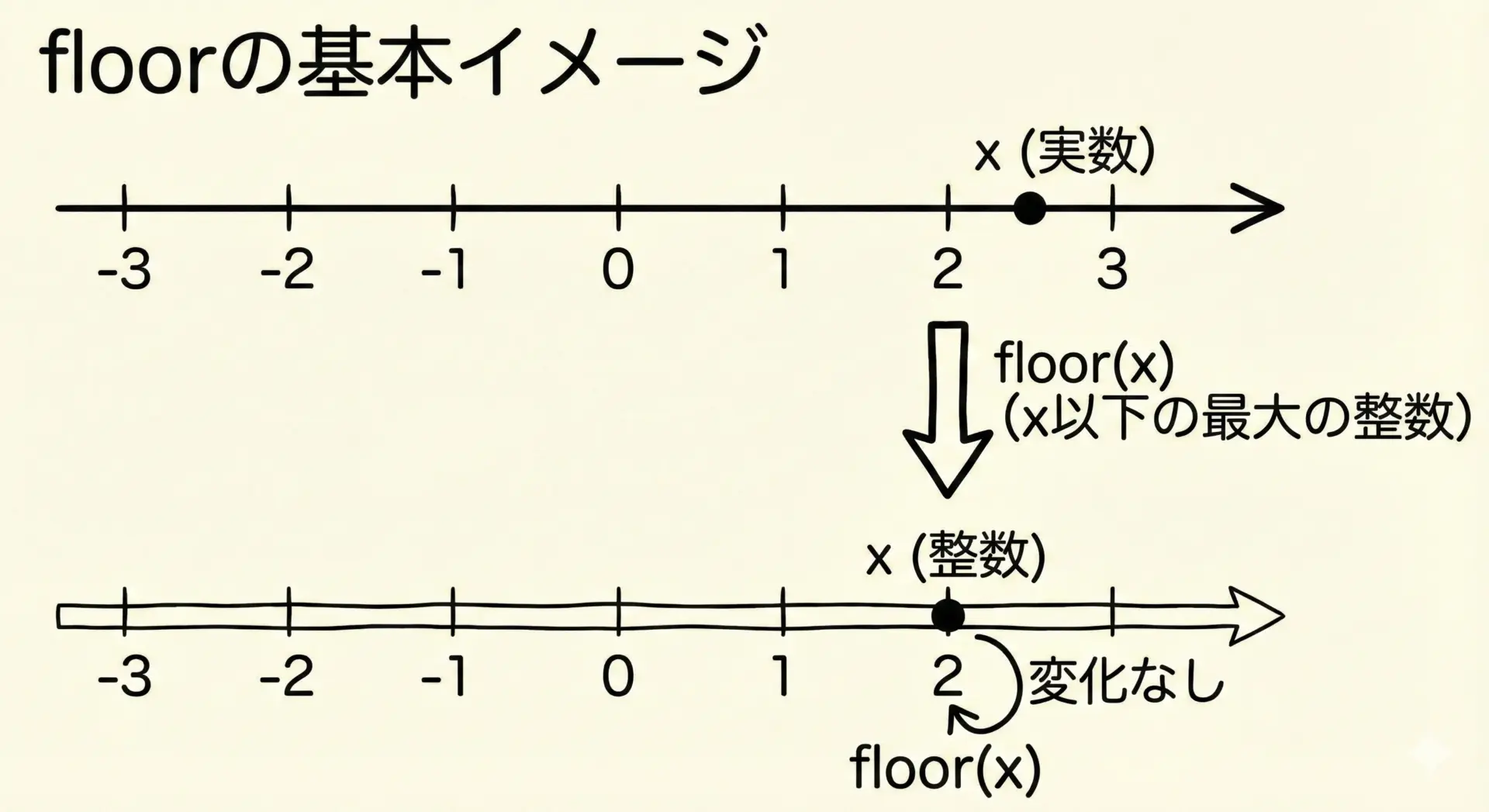
C言語でfloor関数を使う場合も、math.hをインクルードします。
#include <math.h>宣言は、一般的に次の通りです。
double floor(double x);ceilと同様に、float版とlong double版も用意されています。
float floorf(float x);long double floorl(long double x);
基本的な使用例を示します。
#include <stdio.h>
#include <math.h>
int main(void) {
double x1 = 2.3;
double x2 = 2.0;
double x3 = -2.3;
double r1 = floor(x1); // 2.3以下の最大の整数 → 2.0
double r2 = floor(x2); // 2.0以下の最大の整数 → 2.0
double r3 = floor(x3); // -2.3以下の最大の整数 → -3.0
printf("floor(2.3) = %.1f\n", r1);
printf("floor(2.0) = %.1f\n", r2);
printf("floor(-2.3) = %.1f\n", r3);
return 0;
}floor(2.3) = 2.0
floor(2.0) = 2.0
floor(-2.3) = -3.0こちらもceilと同じく、戻り値はdouble型である点に注意が必要です。
正数・負数でのfloorの動作例
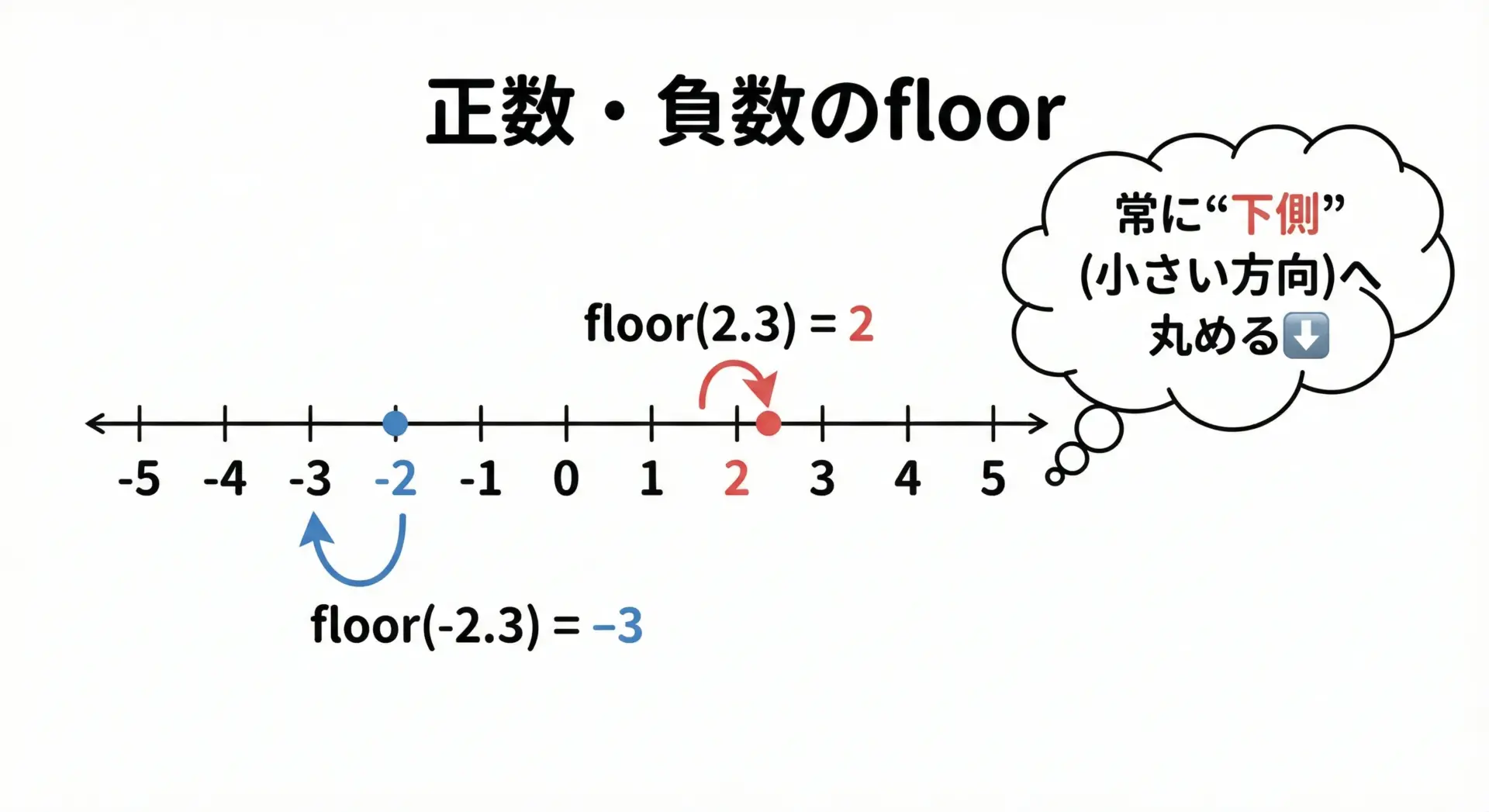
floorは、常に数直線の左側(小さい値)へ丸めます。
#include <stdio.h>
#include <math.h>
int main(void) {
double values[] = { 2.1, 2.9, -2.1, -2.9, 0.0 };
int i;
for (i = 0; i < 5; i++) {
double x = values[i];
double r = floor(x);
printf("x = %5.1f -> floor(x) = %5.1f\n", x, r);
}
return 0;
}x = 2.1 -> floor(x) = 2.0
x = 2.9 -> floor(x) = 2.0
x = -2.1 -> floor(x) = -3.0
x = -2.9 -> floor(x) = -3.0
x = 0.0 -> floor(x) = 0.0負の数のとき、-2.1が-2.0ではなく-3.0になる点は特に意識しておくと良いです。
floorとキャスト(int)の違いと注意点
「切り捨て」と聞くと、(int)x のようなキャストを思い浮かべる方も多いと思います。
しかし、floor(x)と(int)xは必ずしも同じではありません。
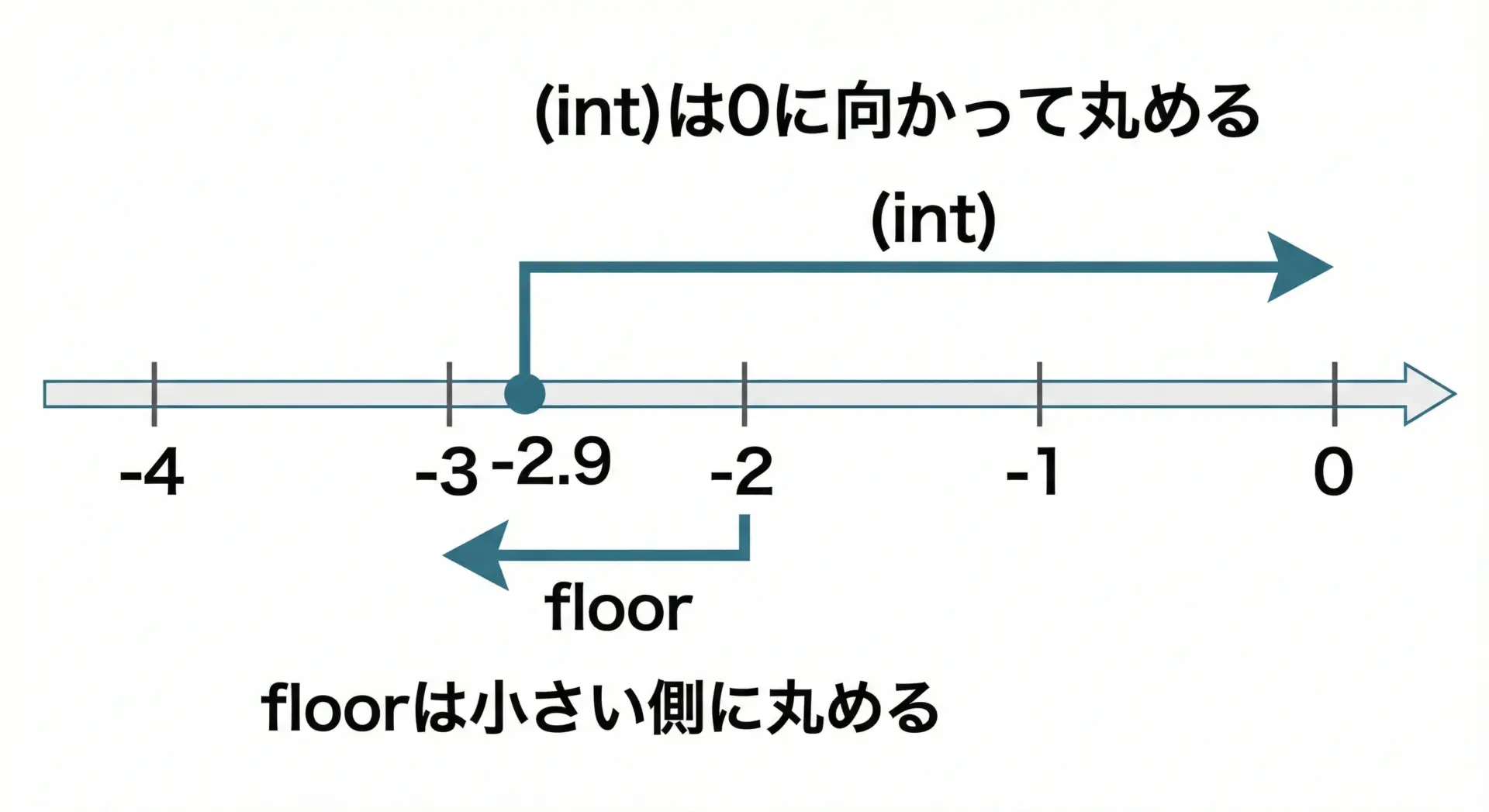
C言語の整数へのキャストは、0に向かって丸める(=小数点以下を単純に捨てる)動作をします。
一方、floorは常に小さい方向に丸めます。
違いをコードで確認してみます。
#include <stdio.h>
#include <math.h>
int main(void) {
double x1 = 2.7;
double x2 = -2.7;
int i1 = (int)x1; // 2.7 → 2
int i2 = (int)x2; // -2.7 → -2 (0に近づく)
double f1 = floor(x1); // 2.7以下の最大の整数 → 2.0
double f2 = floor(x2); // -2.7以下の最大の整数 → -3.0
printf("x1 = %.1f, (int)x1 = %d, floor(x1) = %.1f\n", x1, i1, f1);
printf("x2 = %.1f, (int)x2 = %d, floor(x2) = %.1f\n", x2, i2, f2);
return 0;
}x1 = 2.7, (int)x1 = 2, floor(x1) = 2.0
x2 = -2.7, (int)x2 = -2, floor(x2) = -3.0正の数については(int)xもfloor(x)も同じ結果になりますが、負の数では結果が異なります。
そのため、「数学的な意味での切り捨て」が必要な場合はfloorを使うべきであり、「単に小数点以下を捨てたいだけ」の場合でも、負数を扱うかどうかを意識する必要があります。
整数除算と切り上げ・切り捨ての実装パターン
C言語の整数除算が切り捨てになる理由
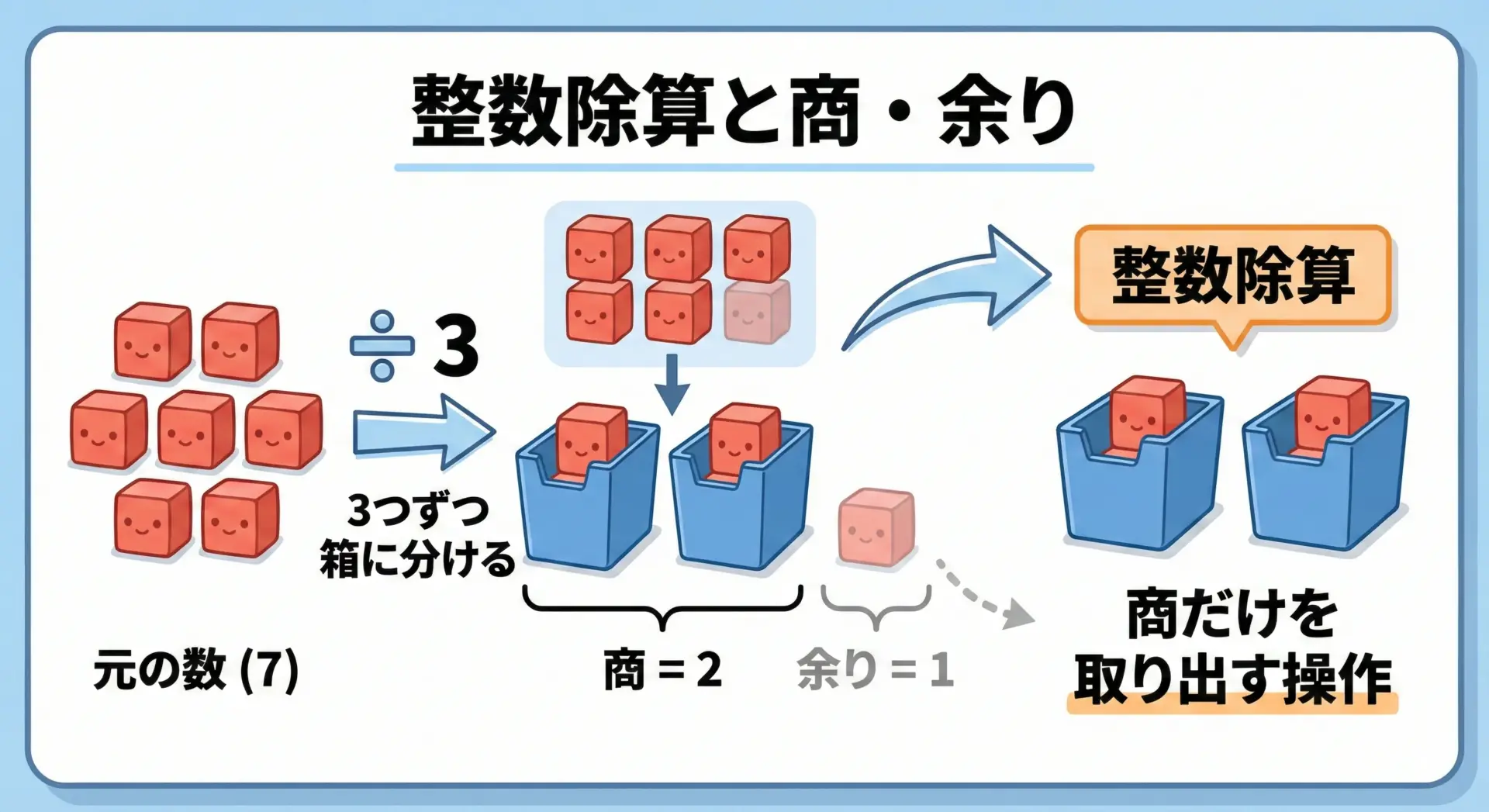
C言語では、整数同士の割り算は商だけを取り出す操作として定義されています。
C99以降の仕様では、整数除算は0に向かって丸めることが規定されています。
例えば、次のようになります。
#include <stdio.h>
int main(void) {
printf("7 / 3 = %d\n", 7 / 3); // 2
printf("-7 / 3 = %d\n", -7 / 3); // -2 (0に近づく)
printf("7 / -3 = %d\n", 7 / -3); // -2
printf("-7 / -3 = %d\n", -7 / -3); // 2
return 0;
}7 / 3 = 2
-7 / 3 = -2
7 / -3 = -2
-7 / -3 = 2この仕様は、商と余りの関係をシンプルに保つためでもあります。
整数a, b(b≠0)について、商qと余りrが
- a = b * q + r
- 0 ≤ |r| < |b|
となるように定義されます。
整数同士の割り算でceil(切り上げ)を実現する方法
整数同士の割り算では結果が切り捨てられてしまうため、「余りが出たら切り上げたい」というケースでは工夫が必要です。
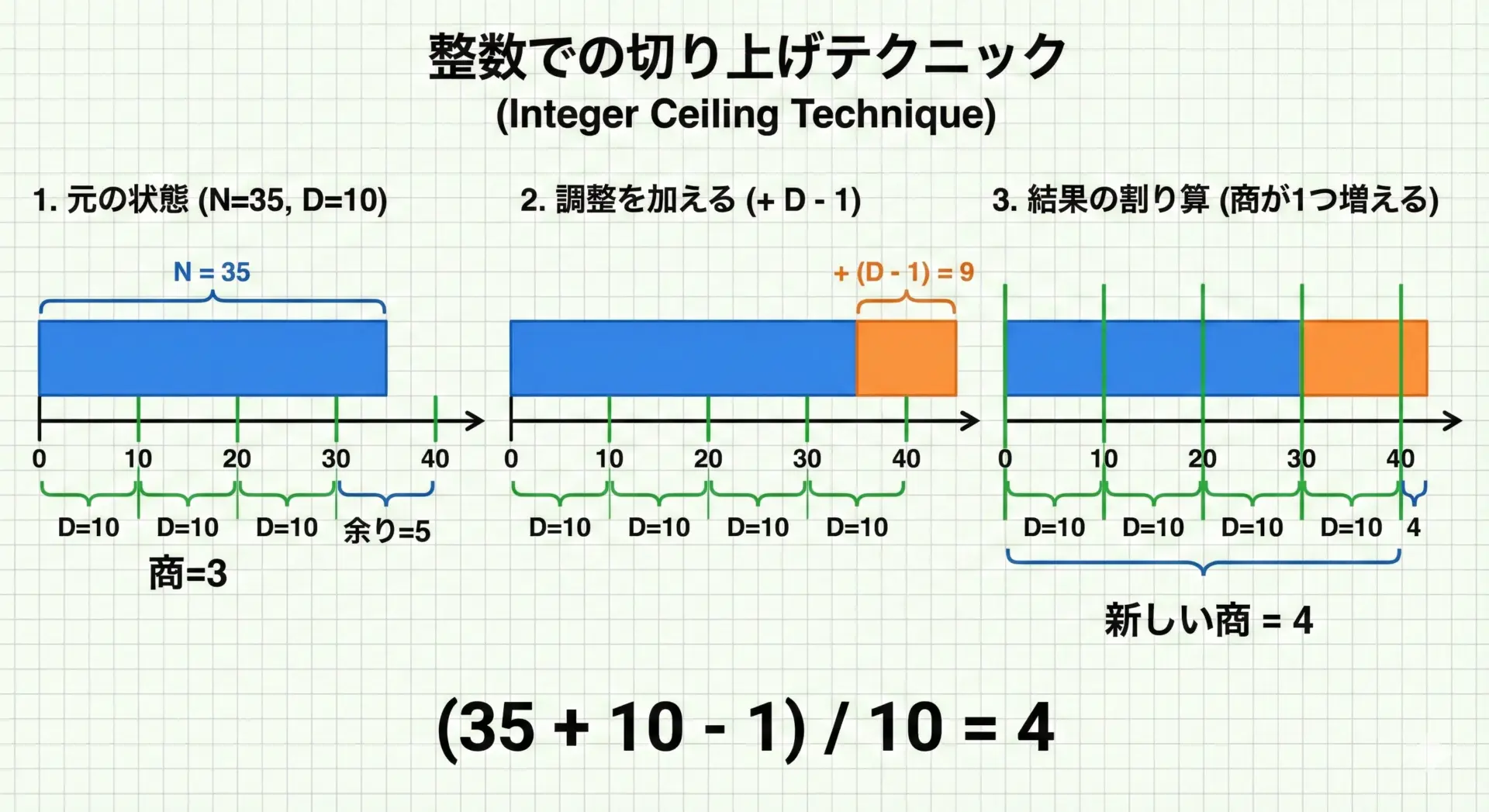
代表的なパターンは、次の式です。
(a + b - 1) / b
これは、a / bを切り上げた整数値を求めるときに使われます。
具体例を見てみましょう。
#include <stdio.h>
int ceil_div(int a, int b) {
// 正の数同士を想定した簡易的なceil除算
return (a + b - 1) / b;
}
int main(void) {
int a = 35;
int b = 10;
int q_trunc = a / b; // 通常の整数除算(切り捨て)
int q_ceil = ceil_div(a, b); // 上記のceil除算
printf("a = %d, b = %d\n", a, b);
printf("a / b = %d\n", q_trunc);
printf("ceil_div(a, b) = %d\n", q_ceil);
return 0;
}a = 35, b = 10
a / b = 3
ceil_div(a, b) = 4なぜこれで切り上げになるかを簡単に説明します。
- a を b で割るとき、a = b * q + r (0 ≤ r < b) と書けます。
- r が 0 なら、a はちょうど b で割り切れています。
- r が正なら、商を1だけ増やしたいです。
ここで、a + b - 1を考えると、
- r = 0 のとき: a + b – 1 = b * q + (b – 1)
→ (a + b – 1) / b = q - r > 0 のとき: a + b – 1 = b * q + r + b – 1 = b * (q + 1) + (r – 1)
→ (a + b – 1) / b = q + 1
このように、割り切れるときはもとの商、割り切れないときは商+1が得られます。
なお、このテクニックは主に正の整数同士の場合に安全です。
負数が絡む場合は別途ロジックを検討する必要があります。
整数同士の割り算でfloor(切り捨て)を明示する方法
整数同士の割り算はそもそも切り捨て(0方向への丸め)なので、多くの場合はa / bを書くだけで充分です。
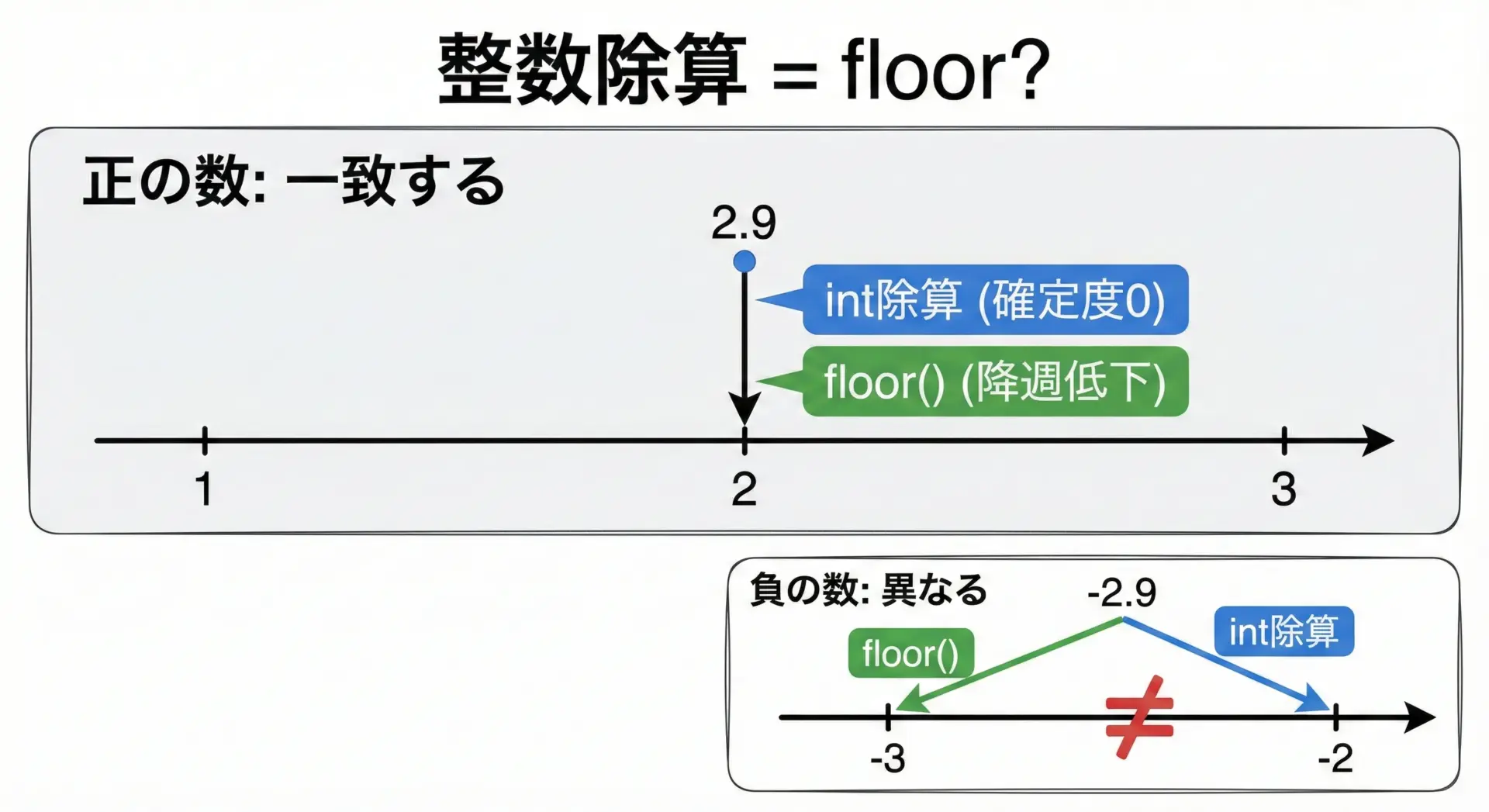
ただし、数学的な意味でのfloor(a / b)を整数だけで実現したい場合、正負を問わず扱うときには注意が必要です。
例として、正の整数同士に限定するなら、次のように「floorと同じ挙動」と言って差し支えありません。
#include <stdio.h>
int main(void) {
int a = 35;
int b = 10;
int q = a / b; // 正の数同士なら floor(35.0 / 10.0) と同じ
printf("a = %d, b = %d\n", a, b);
printf("a / b (floor相当) = %d\n", q);
return 0;
}a = 35, b = 10
a / b (floor相当) = 3一方、負の数を含む場合に「数学のfloor」と一致させたいときは、場合分けが必要になります。
ここでは概念にとどめますが、例えば次のようなアイデアがあります。
a / bがすでにfloorであればそのまま- そうでなければ、商を1小さくする
ただし、このあたりは用途によって要件が複雑になるため、「正の数だけでよいのか」「負の数も扱うのか」を最初に決めておくことが重要です。
ceil・floorと整数除算の使い分けと注意点
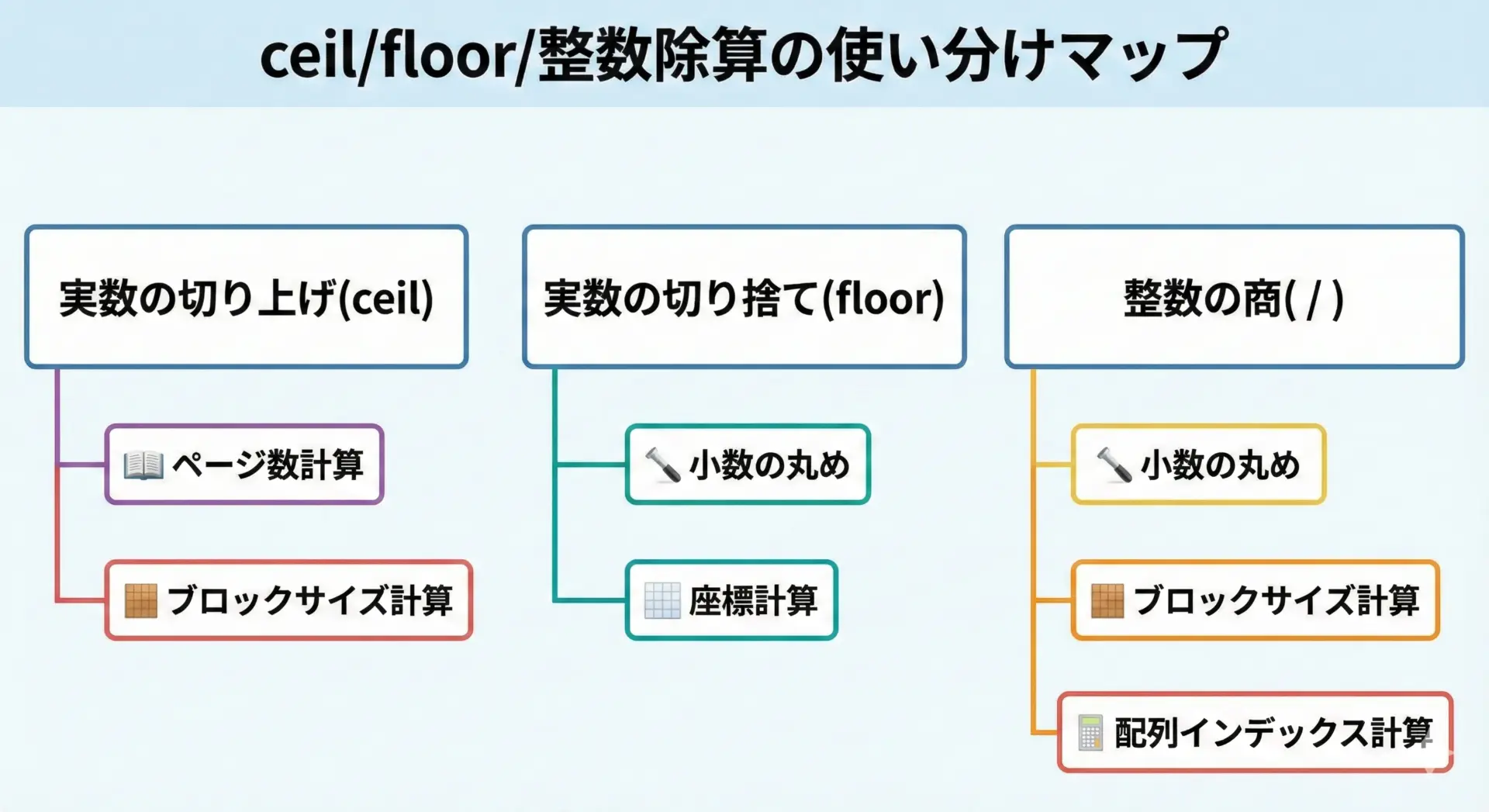
ここまでの内容を踏まえて、どの場面で何を使うべきかを整理します。
1つ目に、実数値を扱う場合です。
金額や測定値など、もともとdoubleで計算している値に対しては、次のようにするのが自然です。
- 「x以上の最小の整数」が欲しい → ceil(x)
- 「x以下の最大の整数」が欲しい → floor(x)
- 結果をintにしたい場合は、
(int)ceil(x)や(int)floor(x)とする
2つ目に、最初から整数同士の計算だけで済ませたい場合です。
例えば、件数やバイト数など、元データが整数であり、精度の観点からも整数だけでやり取りしたいときがあります。
- 単純に商が欲しい → a / b (切り捨て)
- 「割り切れないときは切り上げたい」(ページ数など) → (a + b – 1) / b などのceil相当式
3つ目に、負の数の扱いです。
負の数を扱うとき、次の点に気をつけてください。
floor(x)は常に小さい側(左側)に丸める(int)xや整数除算a / bは0に向かって丸める- そのため、負の数でfloorと(int)や整数除算の結果は一致しない
用途を整理すると、次のように考えると分かりやすいです。
| 状況 | 使うべき手段 |
|---|---|
| 実数値を数学的に「切り上げ」たい | ceil |
| 実数値を数学的に「切り捨て」たい | floor |
| 小数点以下を単に捨てたい(負数もあり得る) | (int)x |
| 正の整数同士の商(切り捨て)が欲しい | a / b |
| 正の整数同士で割り算の結果を切り上げたい | (a + b – 1) / b |
「どの方向に丸めたいのか」「負の数を扱うのか」を意識しておけば、ceil・floor・整数除算を安全に使い分けることができます。
まとめ
本記事では、C言語におけるceil・floorと整数除算について、基本的な挙動から実践的な利用パターンまで詳しく解説しました。
特に、整数同士の割り算が自動的に切り捨てになること、ceil・floorは戻り値がdoubleであること、そして負の数でfloorと(int)の結果が異なる点は、バグを防ぐうえで重要なポイントです。
実数計算ではceil・floorを素直に使い、整数計算では(a + b – 1) / bのような定番テクニックを活用しながら、用途に応じて丸め方を選べるようになれば、より堅牢なC言語プログラムを書くことができるようになります。