C言語でベクトルの向きや2次元座標から角度を求めたいとき、atan2関数は非常に強力な道具になります。
単純なatanでは誤判定しやすいケースも、atan2を使えば安全かつ直感的に処理できます。
本記事では、atan2とは何かから、atanとの違い、使うときの注意点や実用的なサンプルまで、図解とコード例を交えて詳しく解説します。
atan2関数とは
atan2関数の概要と特徴
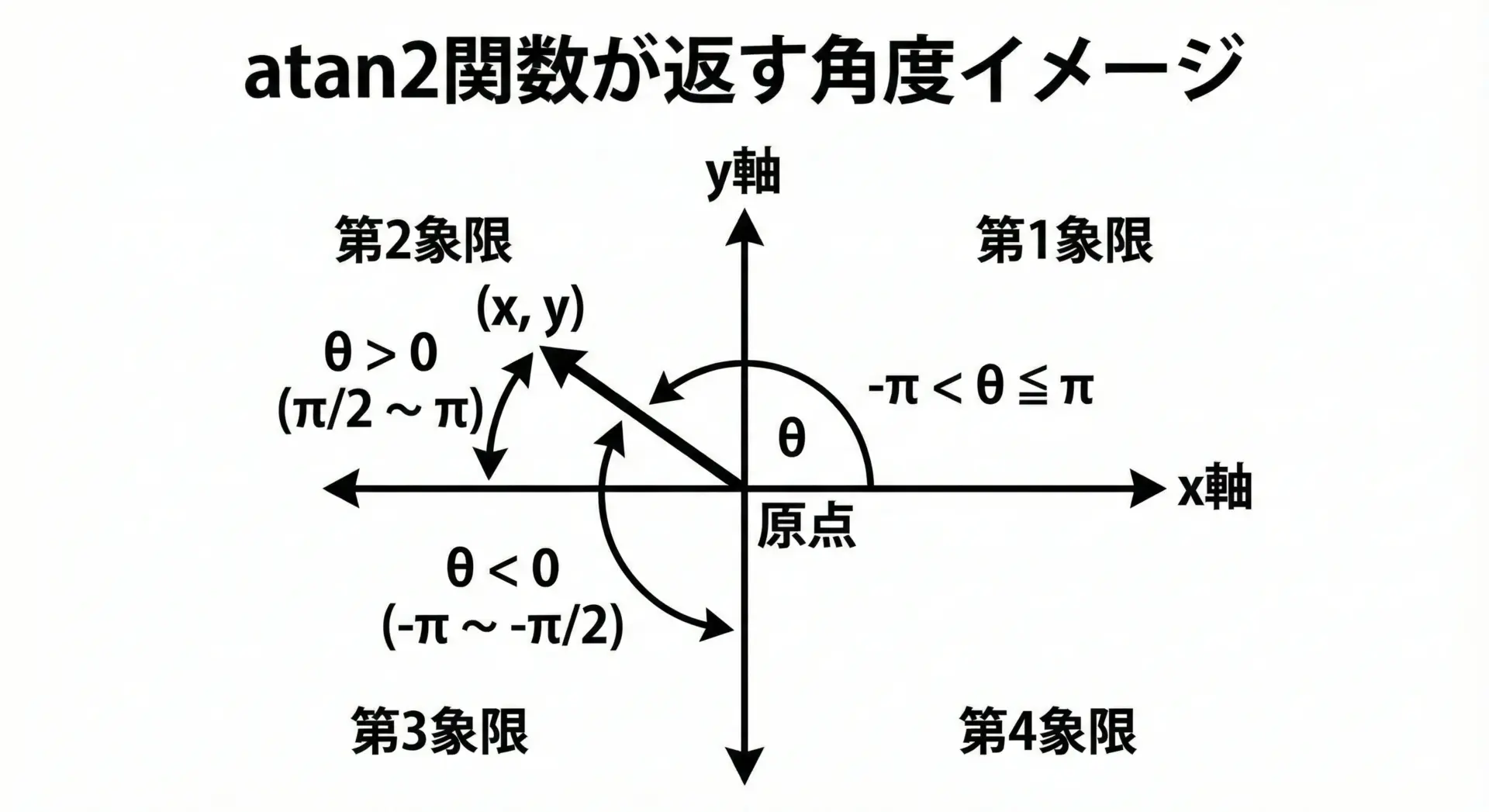
atan2関数は、C言語の数学ライブラリmath.hに含まれる関数で、2次元座標(x, y)から、その点へのベクトルがx軸となす角度を求めるために用いられます。
単純な逆三角関数atanと異なり、引数が2つ(yとx)であることが大きな特徴です。
一般的な特徴をまとめると次のようになります。
- 引数は
(y, x)の2つで、y座標とx座標を指定します。 - 戻り値はラジアン(radian)で表される角度です。
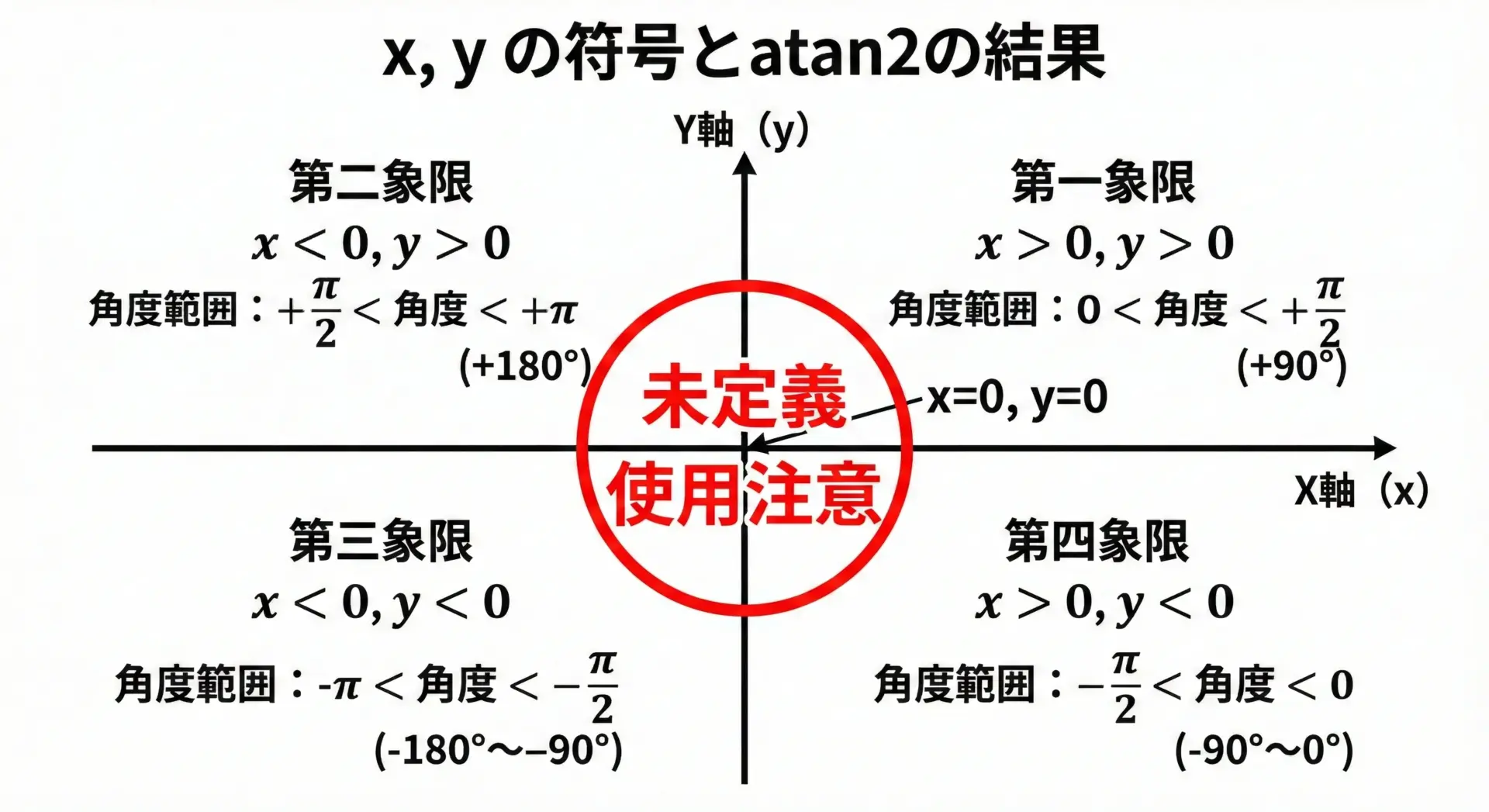
- 戻り値の範囲は[-π, π]で、第1象限から第4象限まですべての象限を区別できます。
- xやyが負の値やゼロを含んでいても、適切に角度を返します。
このように、atan2関数は2次元空間における「向き」を正確に求めるための関数です。
atan2が解く問題
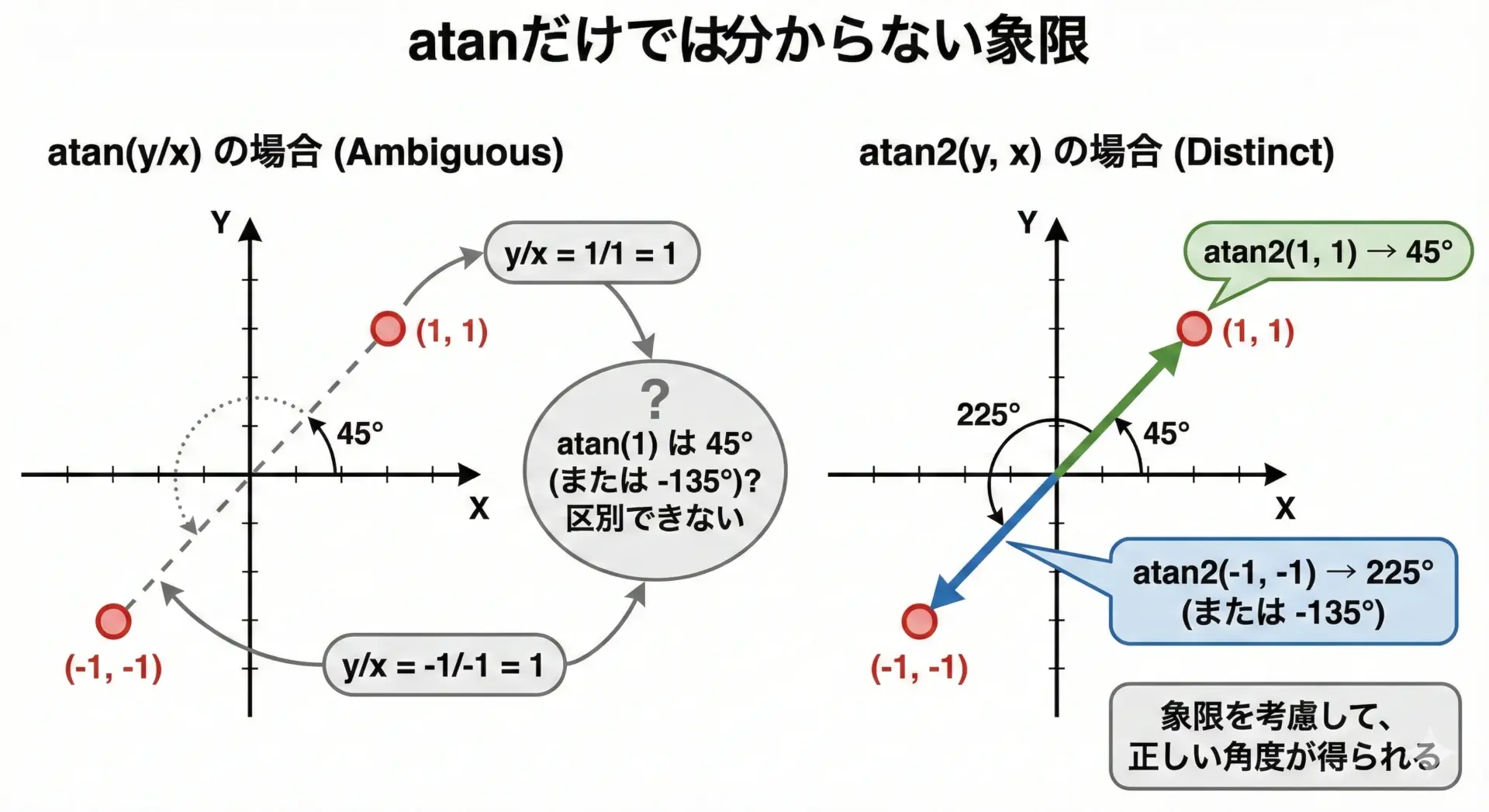
三角関数のtanθは、y/xの比で定義されています。
そのため、atan(y/x)を使うと、y/xが同じ比であれば同じ角度を返してしまいます。
例えば、点(1, 1)と(-1, -1)は、どちらもy/x = 1なので、通常のatanでは同じ角度になってしまいます。
しかし、実際には次のように象限が異なります。
- (1, 1) は第1象限
- (-1, -1) は第3象限
この2つは明らかに向きが180度異なるベクトルですが、atanはこれを区別できません。
ここで役立つのがatan2(y, x)です。
atan2はyとxの符号(正負)を使ってどの象限にあるかを判定し、適切な角度を返してくれます。
つまり、atan2は「比」だけでなく「どちらが正か負か」も考慮して角度を決める関数だと考えると理解しやすいです。
atan2関数の基本的な使い方
atan2の関数プロトタイプと引数の意味
C言語標準ライブラリで定義されているatan2のプロトタイプは次のとおりです。
#include <math.h>
/* 倍精度版 */
double atan2(double y, double x);
/* 単精度版(C99以降) */
float atan2f(float y, float x);
/* 拡張精度版(C99以降) */
long double atan2l(long double y, long double x);ここで重要なのは、引数の順番が(y, x)である点です。
座標としては(x, y)という順番が一般的ですが、atan2はatan2(y, x)という順序になっているため、間違えやすいところです。
それぞれの引数の意味は次のとおりです。
- 第1引数
y
原点から見た縦方向の成分(高さ)を表します。数学的にはsinと関係が深い成分です。 - 第2引数
x
原点から見た横方向の成分を表します。こちらはcosと関係する成分です。
座標(x, y)から角度を求めたいときは、atan2(y, x)と呼び出します。
「座標の順番」と「関数の引数の順番」が逆になっているため、コードを書く際には注意が必要です。
atan2の戻り値の範囲とラジアンの扱い
atan2が返す値はdouble(またはfloatなど)型のラジアン角です。
戻り値の範囲は次のとおりです。
- 範囲: -π 以上 π 以下
つまり[-M_PI, M_PI]に相当します。
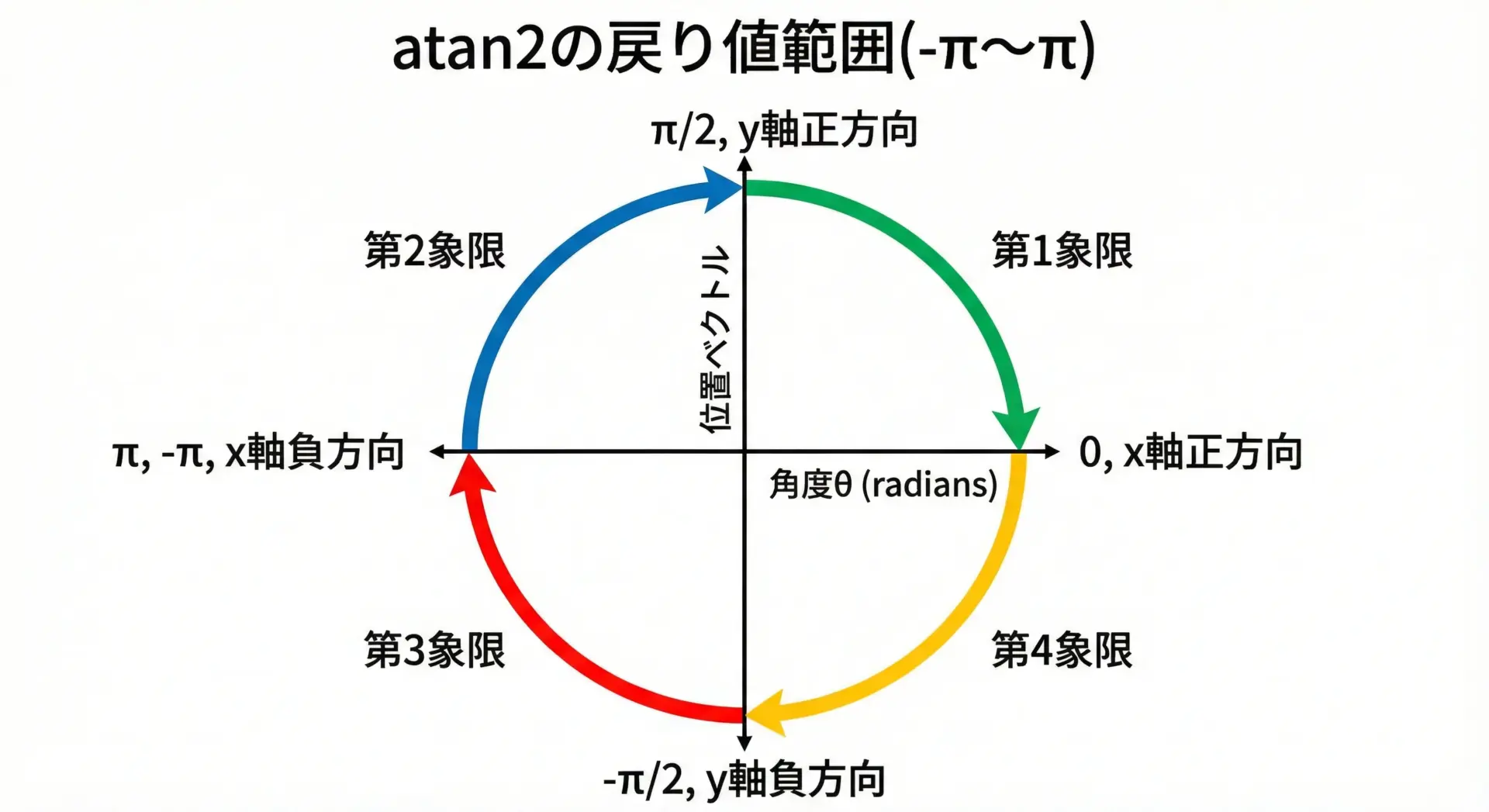
ラジアンは、円周を2πで割った単位で、次のような関係があります。
- 0ラジアン … x軸正方向
- π/2ラジアン … y軸正方向
- -π/2ラジアン … y軸負方向
- πラジアン(または-πラジアン) … x軸負方向
度数法(degree)との変換は次の関係で行います。
- ラジアン → 度
degree = radian * 180.0 / M_PI; - 度 → ラジアン
radian = degree * M_PI / 180.0;
atan2の戻り値は必ずラジアンですので、画面表示やGUI、ゲーム開発などで度数が必要な場合は、自分で変換する必要があります。
atan2の簡単なコード例と出力結果
ここでは、いくつかの代表的な座標についてatan2を実行し、その結果を確認してみます。
#include <stdio.h>
#include <math.h> // atan2, M_PI を使うために必要
int main(void) {
/* 代表的な座標の例 */
double x_values[] = { 1.0, 0.0, -1.0, 0.0, 1.0, -1.0 };
double y_values[] = { 0.0, 1.0, 0.0, -1.0, 1.0, -1.0 };
const char *labels[] = {
"(1, 0)", "(0, 1)", "(-1, 0)", "(0, -1)", "(1, 1)", "(-1, -1)"
};
int n = (int)(sizeof(x_values) / sizeof(x_values[0]));
for (int i = 0; i < n; i++) {
double x = x_values[i];
double y = y_values[i];
/* atan2は(y, x)の順番に注意 */
double rad = atan2(y, x);
/* ラジアンを度数に変換して分かりやすく表示 */
double deg = rad * 180.0 / M_PI;
printf("point %s: atan2(y, x) = %f [rad], %f [deg]\n",
labels[i], rad, deg);
}
return 0;
}実行結果の一例は次のようになります(環境により小数点以下は多少異なります)。
point (1, 0): atan2(y, x) = 0.000000 [rad], 0.000000 [deg]
point (0, 1): atan2(y, x) = 1.570796 [rad], 90.000000 [deg]
point (-1, 0): atan2(y, x) = 3.141593 [rad], 180.000000 [deg]
point (0, -1): atan2(y, x) = -1.570796 [rad], -90.000000 [deg]
point (1, 1): atan2(y, x) = 0.785398 [rad], 45.000000 [deg]
point (-1, -1): atan2(y, x) = -2.356194 [rad], -135.000000 [deg]この結果から、例えば(-1, -1)に対しては-135度が返されており、第3象限の向きを正しく表現していることが分かります。
atan2関数とatan関数の違い
atanとatan2の処理の違い
C言語にはatanという関数も存在し、こちらは「逆正接(逆tan)」を計算します。
プロトタイプは次のようになっています。
#include <math.h>
/* 倍精度版 */
double atan(double x);
/* 単精度版(C99以降) */
float atanf(float x);
/* 拡張精度版(C99以降) */
long double atanl(long double x);atanはxをtanθとみなし、そのときの角度θを-π/2からπ/2の範囲で返します。
つまり、
atan(tanθ) = θ(ただしθは-π/2 < θ < π/2内)
という関係を満たすように動作します。
一方でatan2(y, x)はyとxの比を使いながらも、yとxの符号から象限を判定して-π〜πの範囲で角度を返します。
ですので、次のように考えると分かりやすいです。
- atan: 比
y/xだけ見て、-π/2〜π/2の範囲で角度を返す。 - atan2: 比に加えて符号(象限)も見て、-π〜πの範囲で角度を返す。
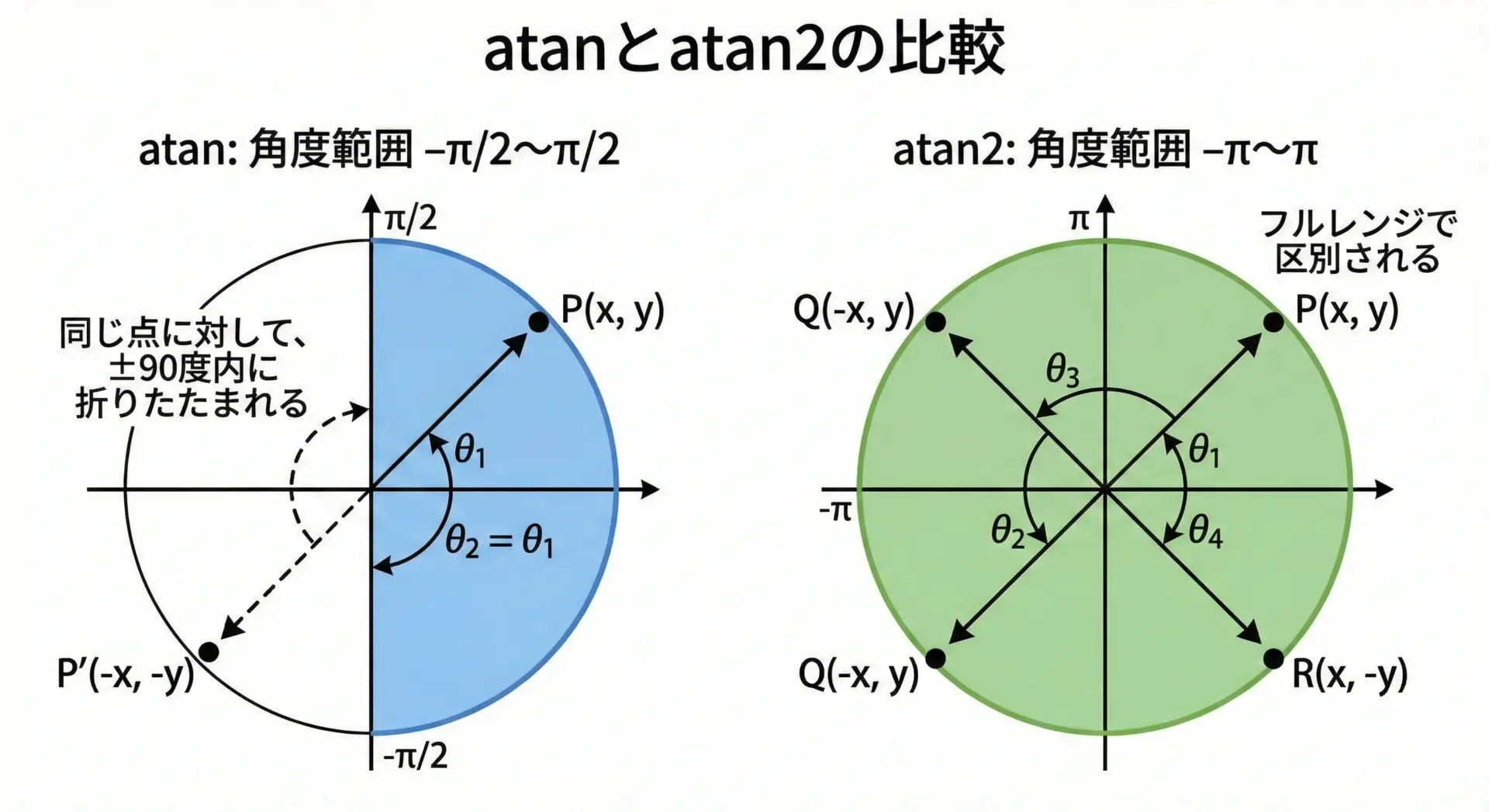
atanでは判定できないケースとatan2の優位性
atanを使うと、次のような問題が発生します。
- xの符号が分からない
atanに与える引数はy/xの比のみです。そのため、元のyとxが両方正だったのか、両方負だったのか、片方だけ負だったのかが分かりません。 - 第2象限・第3象限を区別しづらい
例えば、y/x = 1に対しては、atanは約45度(π/4)しか返しません。しかし、実際には(1, 1)と(-1, -1)では向きが180度異なります。 - x=0のときに計算できない
atan(y/x)という形で書くと、x=0のときにゼロ除算エラーになってしまいます。
これに対してatan2は次のような利点があります。
- yとxの符号を使って、第1〜第4象限を自動的に判断する。
- x=0のときも安全に使える(内部で特別扱いされる)。
- 2次元座標から角度を求める用途に最適化されている。
そのため、2次元座標から角度を求める場合は、原則としてatanではなくatan2を使うべきだと言えます。
具体例で比較するatanとatan2の使い分け
次のサンプルコードでは、同じ座標についてatan(y/x)とatan2(y, x)を比較し、違いを確認してみます。
#include <stdio.h>
#include <math.h>
int main(void) {
/* 例として4つの座標を用意 */
double x_values[] = { 1.0, -1.0, -1.0, 0.0 };
double y_values[] = { 1.0, 1.0, -1.0, 1.0 };
const char *labels[] = {
"( 1, 1)", "(-1, 1)", "(-1, -1)", "( 0, 1)"
};
int n = (int)(sizeof(x_values) / sizeof(x_values[0]));
for (int i = 0; i < n; i++) {
double x = x_values[i];
double y = y_values[i];
printf("point %s\n", labels[i]);
if (x != 0.0) {
/* x!=0のときだけ、比較のためにatan(y/x)を計算 */
double ratio = y / x;
double rad_atan = atan(ratio);
double deg_atan = rad_atan * 180.0 / M_PI;
printf(" atan(y/x) = %8.3f [deg] (ratio=%5.2f)\n",
deg_atan, ratio);
} else {
printf(" atan(y/x) = 計算不能 (x=0 のため 0除算)\n");
}
/* atan2はx=0でも安全に使える */
double rad_atan2 = atan2(y, x);
double deg_atan2 = rad_atan2 * 180.0 / M_PI;
printf(" atan2(y, x) = %8.3f [deg]\n\n", deg_atan2);
}
return 0;
}point ( 1, 1)
atan(y/x) = 45.000 [deg] (ratio= 1.00)
atan2(y, x) = 45.000 [deg]
point (-1, 1)
atan(y/x) = -45.000 [deg] (ratio=-1.00)
atan2(y, x) = 135.000 [deg]
point (-1, -1)
atan(y/x) = 45.000 [deg] (ratio= 1.00)
atan2(y, x) = -135.000 [deg]
point ( 0, 1)
atan(y/x) = 計算不能 (x=0 のため 0除算)
atan2(y, x) = 90.000 [deg]特に(-1, 1)や(-1, -1)に注目すると、atanでは
- 比
y/xの符号によって±45度にしかならず、象限を正しく表現できていないこと
が分かります。
一方、atan2では第2象限として135度、第3象限として-135度が返され、直感的な向きになっています。
atan2関数を使うときの注意点と活用例
ゼロや負の値を含む引数の注意点
atan2は、xやyがゼロや負の値であっても、可能な限り妥当な値を返すように設計されています。
ただし、いくつか注意しておきたいポイントがあります。
- x=0 かつ y≠0 の場合yの符号によって、真上か真下の方向として扱われます。
(x=0, y>0)→ 角度は+π/2(90度)(x=0, y<0)→ 角度は-π/2(-90度)
- x<0 の場合
xが負の場合、結果は必ずπ/2〜πまたは-π〜-π/2の範囲になります。これは第2・第3象限を表します。 - x=0 かつ y=0 の場合
これは方向が定義できない特別なケースです。標準規格上、atan2(0, 0)の結果は未定義となっています。多くの実装では0を返しますが、移植性を考えるとこの呼び出しは避けるべきです。
これらを踏まえると、実際のコードでは次のような防御的な書き方をしておくと安全です。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 0.0;
double y = 0.0;
/* 原点(0, 0)かどうかを事前にチェックする例 */
if (x == 0.0 && y == 0.0) {
printf("原点なので向き(角度)は定義できません。\n");
} else {
double rad = atan2(y, x);
double deg = rad * 180.0 / M_PI;
printf("atan2(y, x) = %f [rad], %f [deg]\n", rad, deg);
}
return 0;
}角度(度数法)への変換と表示方法
先ほども触れたように、atan2の戻り値はラジアンです。
しかし、人間には度数(°)のほうが直感的に理解しやすいことが多いです。
度数に変換する標準的な方法は次の式です。
- ラジアンから度数への変換
deg = rad * 180.0 / M_PI;
ここでM_PIはπの定数です。
環境によっては定義されていない場合もあるため、もしコンパイルエラーになる場合は次のように自前で定義してもかまいません。
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif度数で表示する簡単なサンプルコードは次のようになります。
#include <stdio.h>
#include <math.h>
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
int main(void) {
double x = -1.0;
double y = 1.0;
double rad = atan2(y, x);
double deg = rad * 180.0 / M_PI;
printf("座標(%.1f, %.1f) の角度:\n", x, y);
printf(" ラジアン: %f\n", rad);
printf(" 度数 : %f\n", deg);
return 0;
}このように、内部の計算はラジアンで行い、表示のときだけ度数に変換するというスタイルが、C言語や多くの数学ライブラリでは一般的です。
2次元座標から角度を求める実用的なサンプルコード
ここでは、2次元ゲームやシミュレーションなどを想定した、より実用的なサンプルコードを示します。
プレイヤー(自分)の位置とターゲットの位置が与えられたとき、プレイヤーから見たターゲットの方向角を求める例です。
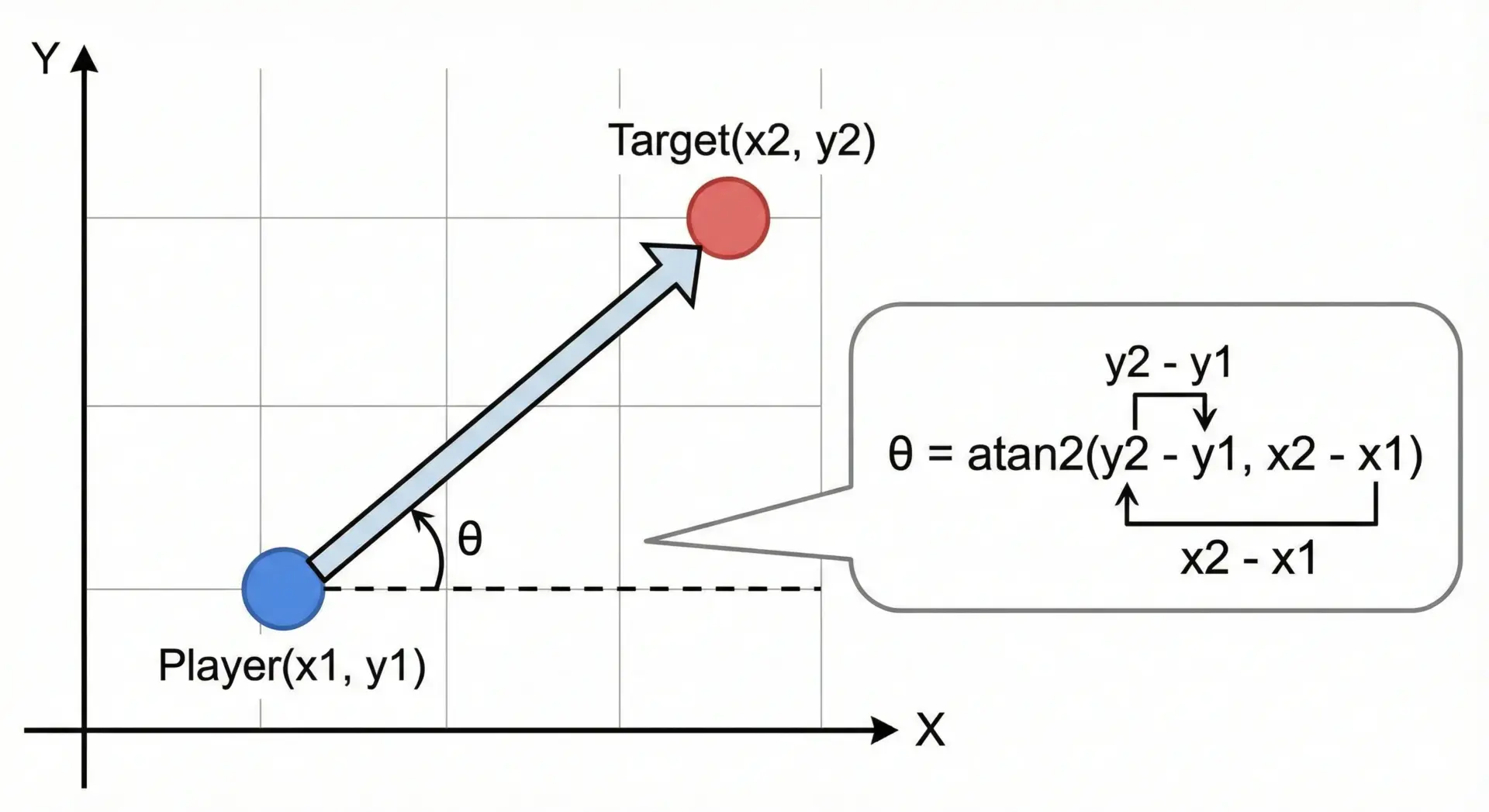
この状況では、プレイヤーを(px, py)、ターゲットを(tx, ty)とすると、ターゲット方向へのベクトルは
dx = tx - px;dy = ty - py;
となります。
この(dx, dy)に対してatan2(dy, dx)を適用すれば、プレイヤーからターゲットへの角度が求まります。
#include <stdio.h>
#include <math.h>
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
/* 2次元座標を表す構造体 */
typedef struct {
double x;
double y;
} Vec2;
/* プレイヤーからターゲットへの角度を求める関数
戻り値はラジアン */
double get_angle_rad(Vec2 player, Vec2 target) {
double dx = target.x - player.x; // x方向の差分
double dy = target.y - player.y; // y方向の差分
/* 原点チェック: 同じ位置なら向きは定義できない */
if (dx == 0.0 && dy == 0.0) {
return 0.0; // ここでは便宜的に0を返す(用途に応じて扱いを決める)
}
/* ベクトル(dx, dy)の向きの角度を求める */
return atan2(dy, dx);
}
/* ラジアンを度数に変換するユーティリティ関数 */
double rad_to_deg(double rad) {
return rad * 180.0 / M_PI;
}
int main(void) {
Vec2 player = { 0.0, 0.0 }; // プレイヤーの位置
Vec2 targets[] = {
{ 1.0, 0.0 }, // 右
{ 0.0, 1.0 }, // 上
{ -1.0, 0.0 }, // 左
{ 0.0, -1.0 }, // 下
{ 1.0, 1.0 }, // 右上(第1象限)
{ -1.0, 1.0 }, // 左上(第2象限)
{ -1.0, -1.0 }, // 左下(第3象限)
{ 1.0, -1.0 }, // 右下(第4象限)
};
int n = (int)(sizeof(targets) / sizeof(targets[0]));
for (int i = 0; i < n; i++) {
Vec2 target = targets[i];
double rad = get_angle_rad(player, target);
double deg = rad_to_deg(rad);
printf("Player(%.1f, %.1f) -> Target(%.1f, %.1f):\n",
player.x, player.y, target.x, target.y);
printf(" 角度: %7.3f [rad], %7.3f [deg]\n\n", rad, deg);
}
return 0;
}Player(0.0, 0.0) -> Target(1.0, 0.0):
角度: 0.000 [rad], 0.000 [deg]
Player(0.0, 0.0) -> Target(0.0, 1.0):
角度: 1.571 [rad], 90.000 [deg]
Player(0.0, 0.0) -> Target(-1.0, 0.0):
角度: 3.142 [rad], 180.000 [deg]
Player(0.0, 0.0) -> Target(0.0, -1.0):
角度: -1.571 [rad], -90.000 [deg]
Player(0.0, 0.0) -> Target(1.0, 1.0):
角度: 0.785 [rad], 45.000 [deg]
Player(0.0, 0.0) -> Target(-1.0, 1.0):
角度: 2.356 [rad], 135.000 [deg]
Player(0.0, 0.0) -> Target(-1.0, -1.0):
角度: -2.356 [rad], -135.000 [deg]
Player(0.0, 0.0) -> Target(1.0, -1.0):
角度: -0.785 [rad], -45.000 [deg]このように、atan2を使うことで2次元ベクトルの向きを簡潔かつ正確に求めることができます。
ゲームではこの角度を使ってスプライトの向きを変えたり、物理シミュレーションでは力の方向を決定したりと、さまざまな場面で応用できます。
まとめ
atan2関数は、2次元座標から角度を求めるための標準的な手段であり、単純なatanでは判定できない象限の違いを正しく扱える点が最大の利点です。
引数の順番が(y, x)であること、戻り値が-π〜πのラジアンで返ってくること、そして(0, 0)の場合は未定義であることを押さえておけば、実用上のトラブルは大きく減らせます。
2次元ベクトルの向きや座標から角度を求める場面では、まずatan2を使うという習慣を身につけると、より安全で分かりやすいコードを書くことができます。

