C言語で図形やゲーム、センサー値の処理などを行うとき、距離から角度を求める場面はとても多くあります。
そのときに欠かせないのが逆三角関数(asin, acos, atan, atan2)です。
本記事では、C言語でこれらの関数を正しく使うために、戻り値や引数の範囲、典型的な用途、注意点、実用的なコード例まで、丁寧に解説していきます。
C言語の逆三角関数とは
逆三角関数(asin, acos, atan)の基本
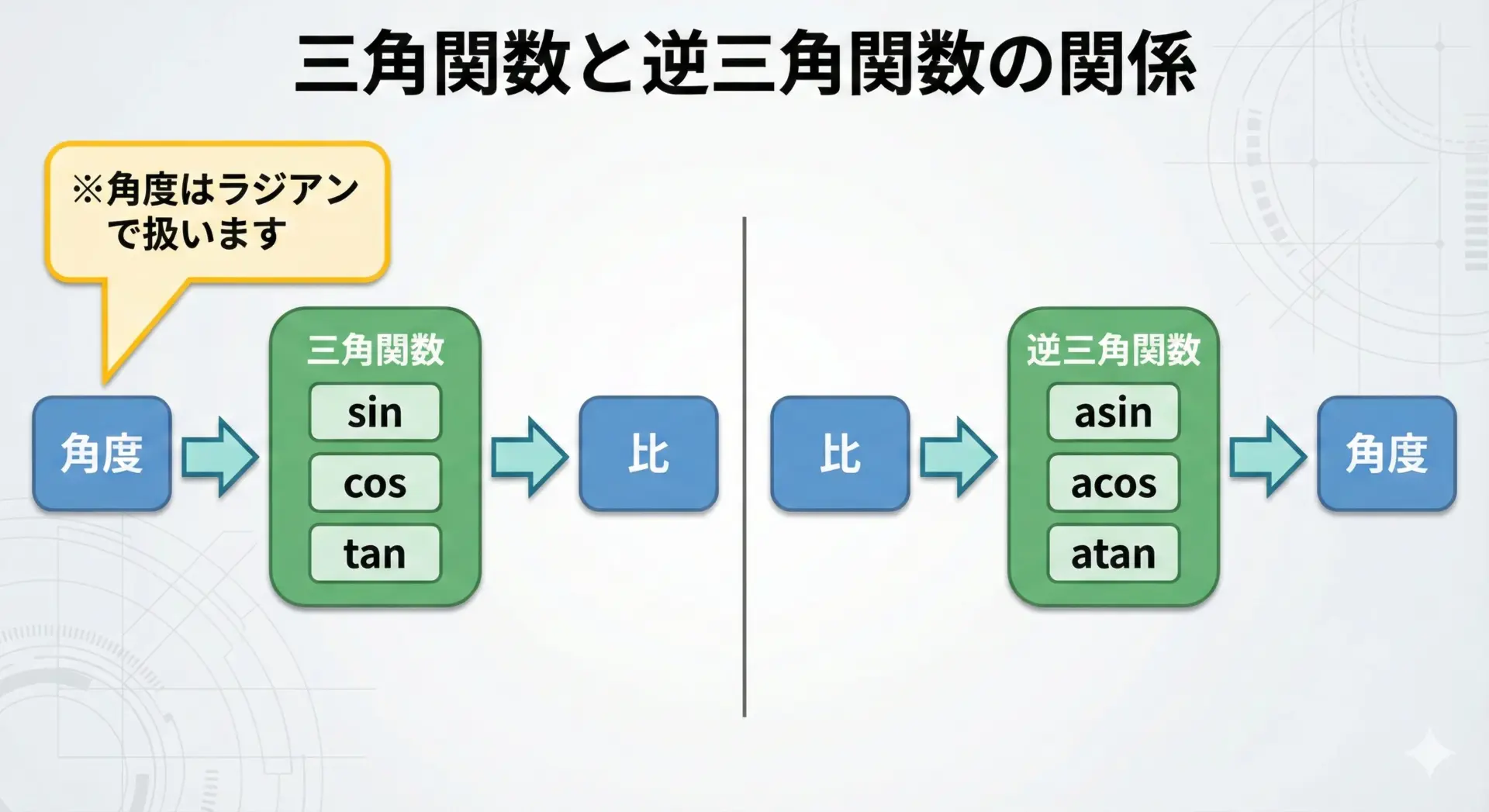
逆三角関数とは、三角関数の「逆計算」をする関数です。
三角関数は角度から比(正弦、余弦、正接)を求めますが、逆三角関数はその逆で、比から角度を求めるものです。
三角関数と逆三角関数の対応関係は次のようになります。
- 正弦(sin)の逆 → 逆正弦(asin)
- 余弦(cos)の逆 → 逆余弦(acos)
- 正接(tan)の逆 → 逆正接(atan)
ここで重要なのは、C言語の数学関数は角度を度(°)ではなくラジアン(rad)で扱うという点です。
例えば、90度はπ/2ラジアン、180度はπラジアンになります。
この関係を理解しておくと、後で出てくる「長さから角度を求める」例がすんなり理解しやすくなります。
角度を求めるときに逆三角関数が必要な理由
長さから角度を求める場面は、実は非常に多いです。
例えば次のような場面を考えてみます。
- 2Dゲームで「プレイヤーから敵への方向」を角度で求めたい
- ロボットアームのリンク長から関節角度を計算したい
- 三角形の3辺の長さから各頂点の角度を計算したい
- センサーで取得した加速度から傾き角度を求めたい
これらはいずれも、三角形の辺の長さ(または座標差)は分かっているが、角度が分からないという状況です。
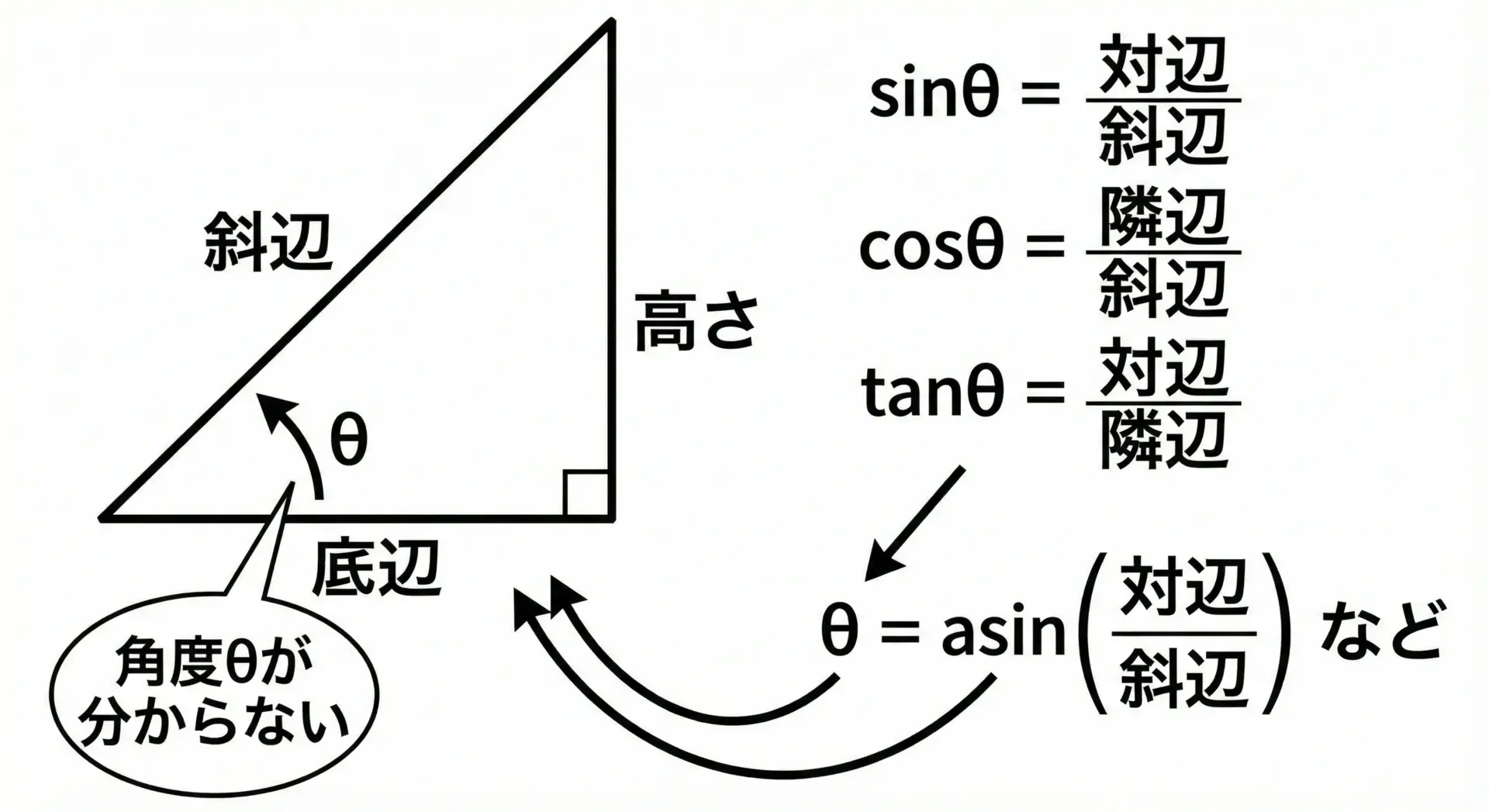
三角関数では例えばsinθ = 対辺/斜辺のように計算しますが、θを求めたいときはこの式を逆に解かなければいけません。
その役割を担うのがasin, acos, atanといった逆三角関数です。
C言語で使える逆三角関数の種類と特徴
C言語では、標準ライブラリmath.hに以下の逆三角関数が用意されています。
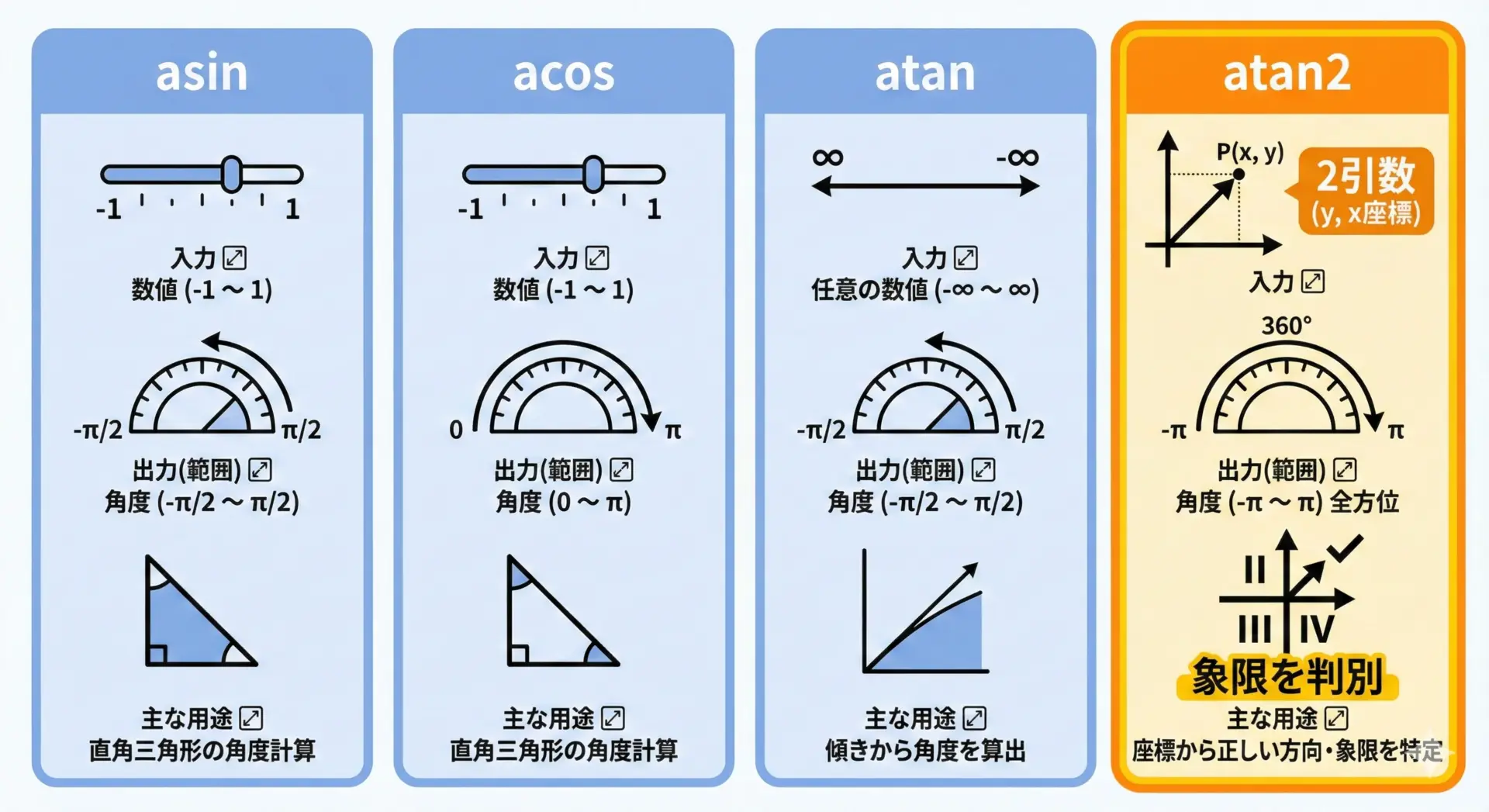
代表的な関数の特徴を表にまとめます。
| 関数名 | 主な役割 | 引数(入力) | 戻り値(範囲) |
|---|---|---|---|
| asin(x) | 逆正弦(arc sin) | 比(x) | [-π/2, π/2] |
| acos(x) | 逆余弦(arc cos) | 比(x) | [0, π] |
| atan(x) | 逆正接(arc tan) | 比(x) | (-π/2, π/2) |
| atan2(y, x) | y/x の逆正接(象限考慮) | y座標, x座標 | (-π, π] |
ポイントとして、atan2は2引数で、座標から角度を求めるときの必須関数です。
後のセクションで詳しく扱います。
asin関数で角度を求める
asin関数の書式と戻り値の範囲
asin関数は、与えられた値を「正弦」とする角度をラジアンで返します。
書式は次のようになります。
#include <math.h>
double asin(double x); // 浮動小数点(double)版
float asinf(float x); // float版
long double asinl(long double x); // long double版戻り値の範囲は[-π/2, π/2]、つまり-90度から+90度までです。
これが「主値」と呼ばれる範囲で、asinはこの中から1つの角度を返します。
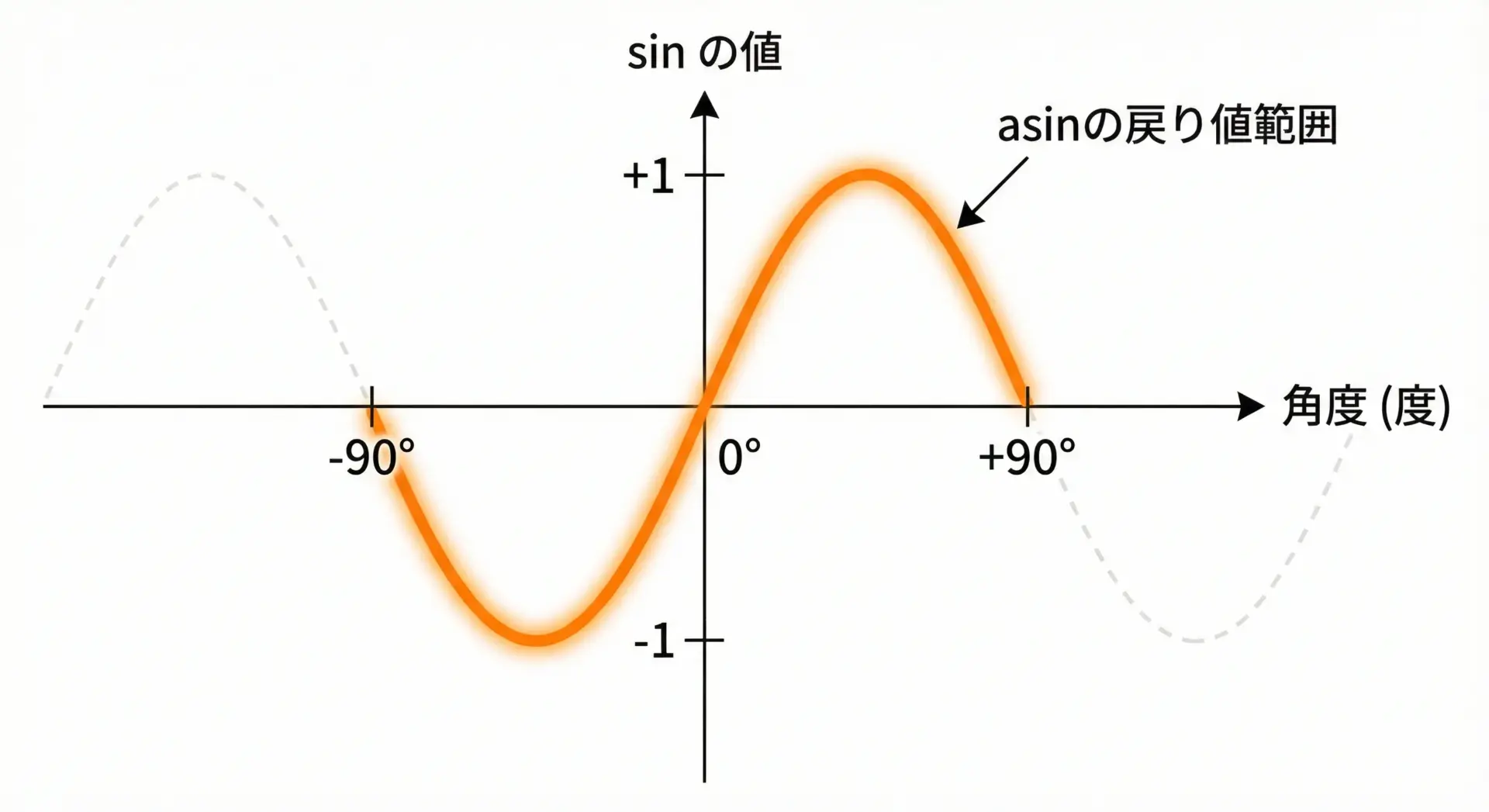
このグラフを見ると、sinは−90度から+90度の間で単調増加なので、その区間だけなら「逆関数」が定義できることが分かります。
これがasinの戻り値がこの範囲に限定される理由です。
asinの引数の範囲とエラーに注意
asinの引数xは、必ず -1.0 以上 +1.0 以下でなければなりません。
これは定義上、正弦の値がその範囲を超えないからです。
- x
< -1.0または x> 1.0の場合、結果は数学的に存在しない - そのため、C言語の実装によってはドメインエラーとして
NaNが返る
計算誤差により、理論上は1.0であるはずが、実際には1.0000001のようになってしまうことがあります。
そのようなときには、引数を明示的に −1.0〜1.0 の範囲に丸める処理を挟むと安全です。
#include <stdio.h>
#include <math.h>
// 値を [-1.0, 1.0] にクランプする関数
double clamp_to_unit(double x) {
if (x < -1.0) return -1.0;
if (x > 1.0) return 1.0;
return x;
}
int main(void) {
double x = 1.0000001; // 計算誤差で少しだけ範囲を超えた値
double s = clamp_to_unit(x);
double rad = asin(s);
printf("元の値 : %.7f\n", x);
printf("クランプ : %.7f\n", s);
printf("asin(s) : %.7f [rad]\n", rad);
return 0;
}元の値 : 1.0000001
クランプ : 1.0000000
asin(s) : 1.5707963 [rad]このように、前処理で範囲を強制することで、意図しないエラーを避けることができます。
ラジアンから度(°)への変換方法とコード例
C言語の数学関数は角度をラジアンで扱いますが、人間が理解しやすいのは度(°)です。
そこで必要になるのがラジアンと度の相互変換です。
変換式は次の通りです。
- ラジアン → 度
degree = radian * 180.0 / M_PI; - 度 → ラジアン
radian = degree * M_PI / 180.0;
M_PIはmath.hで定義されている円周率の定数(実装によっては定義にはマクロ_USE_MATH_DEFINESが必要なこともあります)。
定義されていない場合は自分で#defineしても構いません。
#include <stdio.h>
#include <math.h>
// ラジアンから度への変換関数
double rad2deg(double rad) {
return rad * 180.0 / M_PI;
}
// 度からラジアンへの変換関数
double deg2rad(double deg) {
return deg * M_PI / 180.0;
}
int main(void) {
double rad = M_PI / 2.0; // 90度に相当するラジアン
double deg = rad2deg(rad);
printf("rad = %.6f [rad]\n", rad);
printf("deg = %.6f [deg]\n", deg);
// 度からラジアンに戻してみる
double rad_back = deg2rad(deg);
printf("rad_back = %.6f [rad]\n", rad_back);
return 0;
}rad = 1.570796 [rad]
deg = 90.000000 [deg]
rad_back = 1.570796 [rad]このような変換用の小さな関数を用意しておくと、プログラム全体が読みやすくなります。
長さから角度を求めるasinの具体例
asinは直角三角形の「対辺」と「斜辺」から角度を求めるときに使います。
例えば、斜辺の長さが10、高さ(対辺)が3の直角三角形があったとします。
このとき、底辺と斜辺のなす角度θは次のように求められます。
- sinθ = 対辺 / 斜辺 = 3 / 10
- θ = asin(3 / 10)
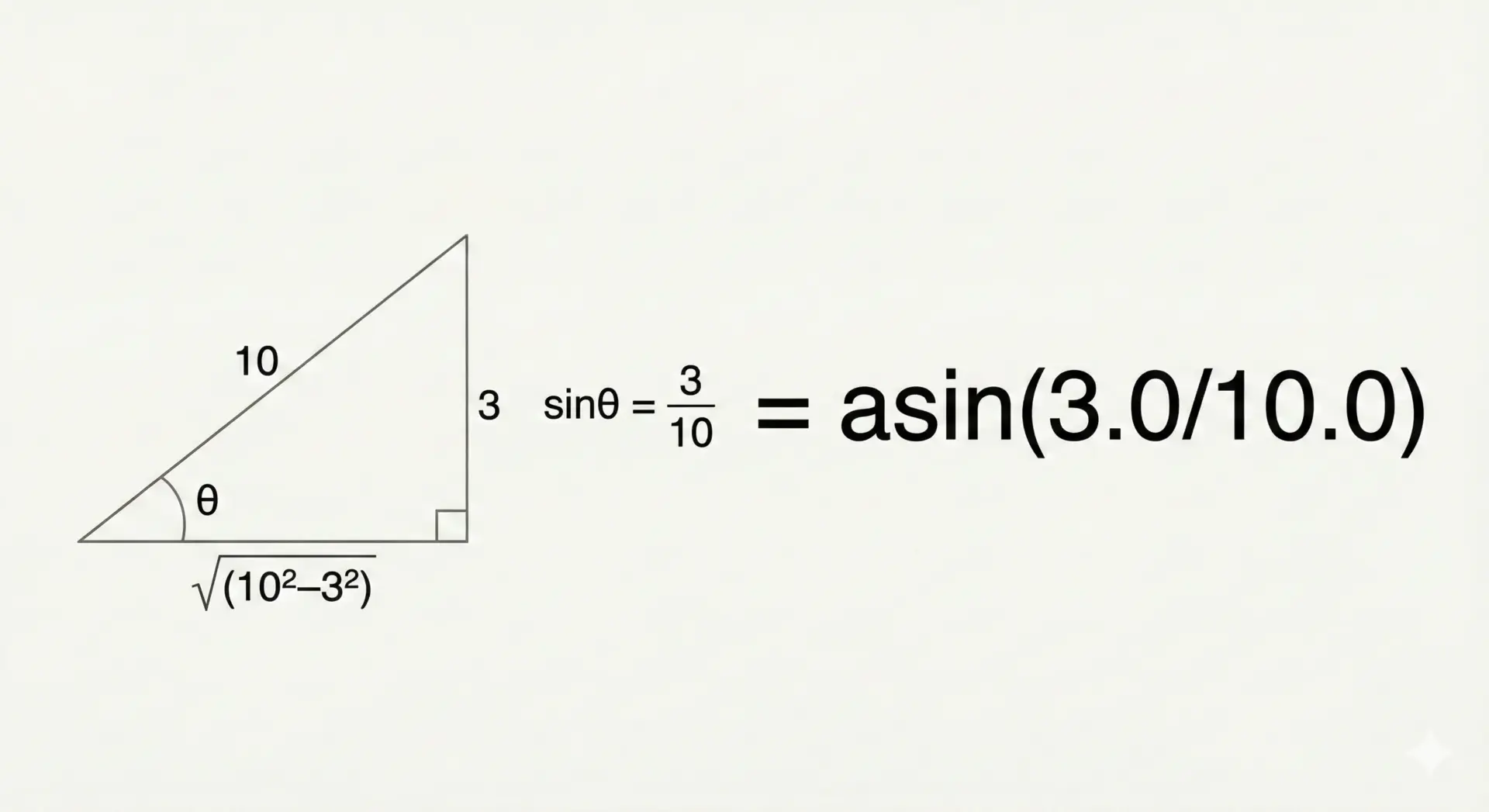
これをC言語で実装すると次のようになります。
#include <stdio.h>
#include <math.h>
double rad2deg(double rad) {
return rad * 180.0 / M_PI;
}
int main(void) {
double hyp = 10.0; // 斜辺の長さ
double opp = 3.0; // 対辺(高さ)の長さ
// sinθ = opp / hyp より、θ = asin(opp / hyp)
double ratio = opp / hyp;
double rad = asin(ratio); // 角度(ラジアン)
double deg = rad2deg(rad); // 角度(度)
printf("対辺 = %.2f, 斜辺 = %.2f\n", opp, hyp);
printf("opp/hyp = %.4f\n", ratio);
printf("θ = %.6f [rad]\n", rad);
printf("θ = %.6f [deg]\n", deg);
return 0;
}対辺 = 3.00, 斜辺 = 10.00
opp/hyp = 0.3000
θ = 0.304693 [rad]
θ = 17.452306 [deg]このように、辺の長さから角度を求めたいときにasinは非常に分かりやすく使えます。
acos関数で角度を求める
acos関数の書式と戻り値の範囲
acos関数は、与えられた値を「余弦」とする角度をラジアンで返します。
書式は次の通りです。
#include <math.h>
double acos(double x); // 浮動小数点(double)版
float acosf(float x); // float版
long double acosl(long double x); // long double版戻り値の範囲は[0, π]、つまり0度から180度です。
これもacosの「主値」の範囲です。
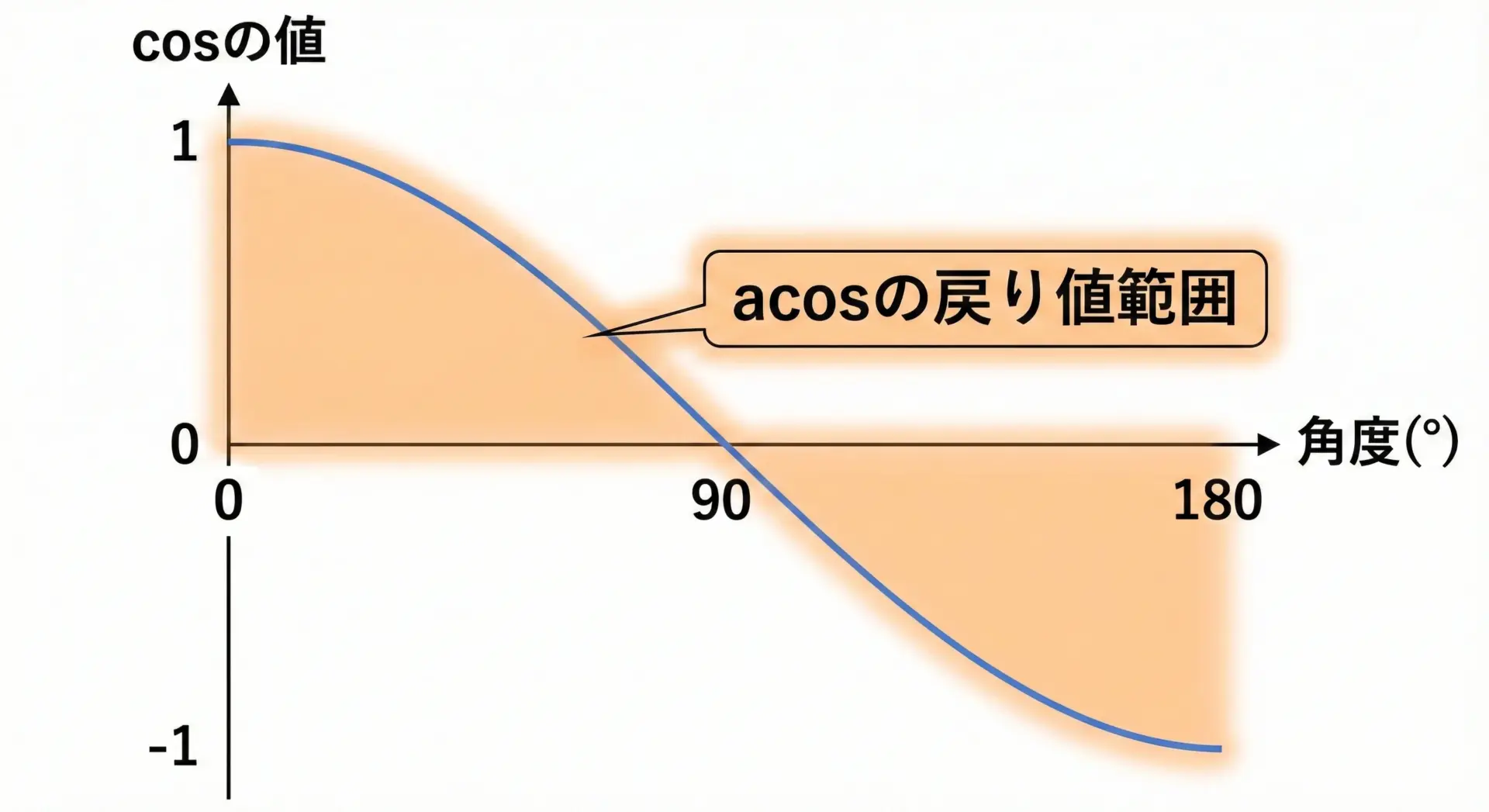
cosはこの範囲で単調減少するため、ここだけなら一対一対応が成り立ち、逆関数としてacosが定義できます。
acosとasinの違いと使い分け
asinとacosはどちらも引数範囲は[-1.0, 1.0]です。
しかし、戻り値の範囲が違います。
| 関数 | 戻り値の範囲 | 主に使う状況 |
|---|---|---|
| asin | [-π/2, π/2] | 対辺/斜辺から鋭角を知りたいとき |
| acos | [0, π] | 余弦(内積)からなす角を求めたいとき |
ベクトルのなす角を求めるときには、しばしばacosが使われます。
その理由は、内積の式が cos を使って表されるからです。
- 2つのベクトルA, Bに対して
A・B = |A||B|cosθ
ここから、cosθ = (A・B) / (|A||B|)
よってθ = acos( (A・B) / (|A||B|) )
一方、単純な直角三角形の鋭角を求めたいだけならasinの方がイメージしやすいことが多いです。
用途に応じて使い分けるとよいです。
ベクトルのなす角を求めるacosのコード例
2次元または3次元のベクトルの間の角度を求める典型的なコード例を示します。
ここでは2Dベクトルを例に説明します。
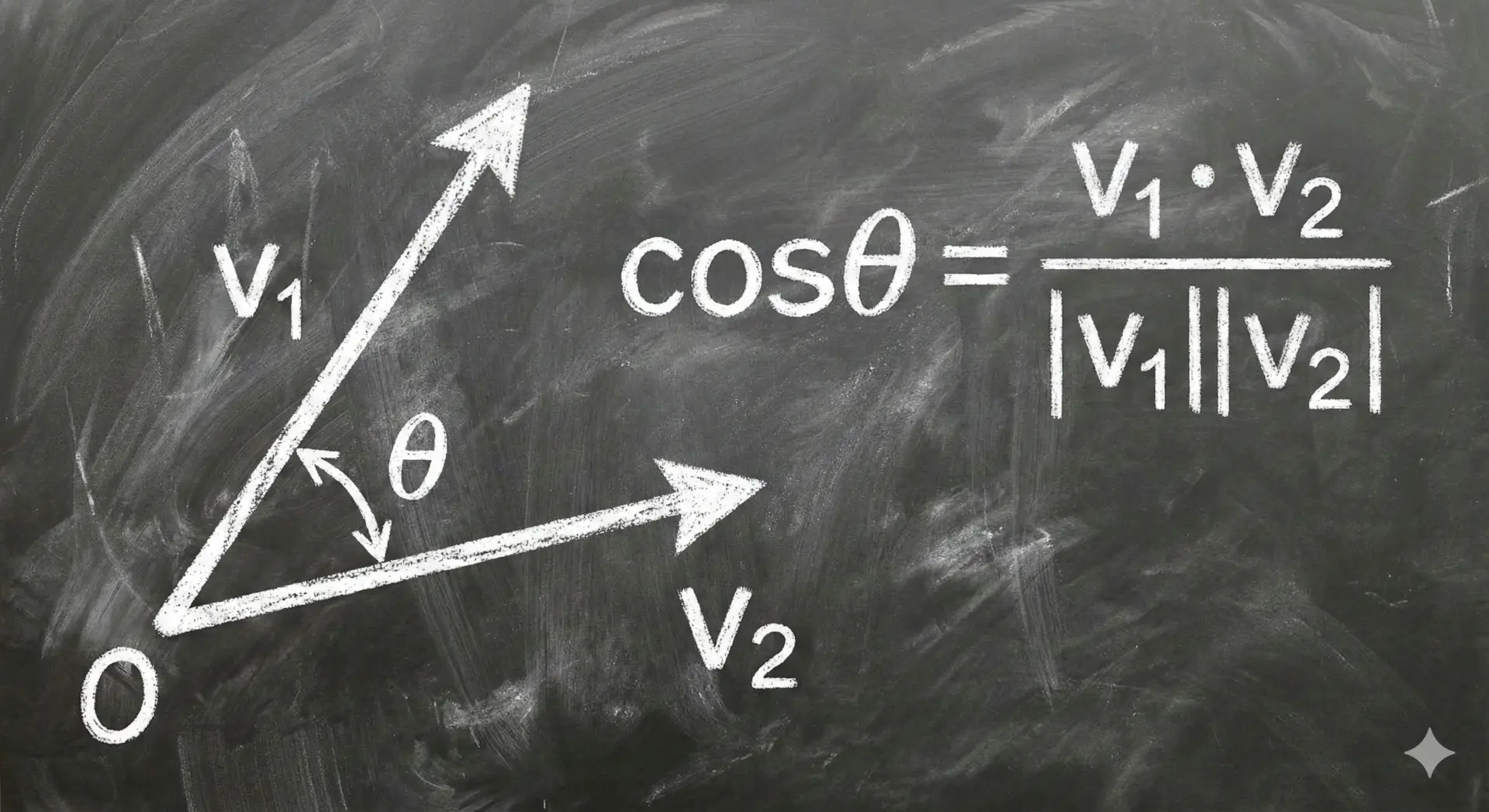
#include <stdio.h>
#include <math.h>
// 2次元ベクトル構造体
typedef struct {
double x;
double y;
} Vec2;
// ベクトルの内積を計算
double dot(Vec2 a, Vec2 b) {
return a.x * b.x + a.y * b.y;
}
// ベクトルの長さ(ノルム)を計算
double length(Vec2 v) {
return sqrt(v.x * v.x + v.y * v.y);
}
// ラジアン→度
double rad2deg(double rad) {
return rad * 180.0 / M_PI;
}
int main(void) {
Vec2 v1 = {1.0, 0.0}; // x軸方向の単位ベクトル
Vec2 v2 = {1.0, 1.0}; // 45度方向のベクトル
double dot_v = dot(v1, v2);
double len_v1 = length(v1);
double len_v2 = length(v2);
double cos_theta = dot_v / (len_v1 * len_v2);
// 計算誤差対策として [-1.0, 1.0] にクランプ
if (cos_theta > 1.0) cos_theta = 1.0;
if (cos_theta < -1.0) cos_theta = -1.0;
double rad = acos(cos_theta);
double deg = rad2deg(rad);
printf("v1 = (%.2f, %.2f)\n", v1.x, v1.y);
printf("v2 = (%.2f, %.2f)\n", v2.x, v2.y);
printf("内積 v1・v2 = %.4f\n", dot_v);
printf("|v1| = %.4f, |v2| = %.4f\n", len_v1, len_v2);
printf("cosθ = %.6f\n", cos_theta);
printf("θ = %.6f [rad]\n", rad);
printf("θ = %.6f [deg]\n", deg);
return 0;
}v1 = (1.00, 0.00)
v2 = (1.00, 1.00)
内積 v1・v2 = 1.0000
|v1| = 1.0000, |v2| = 1.4142
cosθ = 0.707107
θ = 0.785398 [rad]
θ = 45.000000 [deg]このコードでは、ベクトル間の角度θが45度であることが確認できます。
acos使用時のドメインエラー対策
acosもasinと同様に、引数の範囲が[-1.0, 1.0]です。
しかし、ベクトルの内積を正規化した値cosθ = (A・B)/(|A||B|)は、理論的には必ずこの範囲に収まるはずですが、浮動小数点の丸め誤差により1.000000001のようになってしまうことがあります。
このような状況を防ぐには、先ほどの例のようにクランプ処理を必ず入れておくと安心です。
// cos値を [-1.0, 1.0] にクランプするユーティリティ
double clamp_cos(double c) {
if (c > 1.0) return 1.0;
if (c < -1.0) return -1.0;
return c;
}さらに、ゼロ長ベクトルに対して角度を求めようとすると、|A||B|が0になってしまい、0除算につながります。
この場合は、あらかじめ長さが0でないことをチェックし、0ならエラー扱いにするといった対策が有効です。
atan・atan2関数で角度を求める
atan関数の基本と戻り値の範囲
atan関数は、与えられた値を「正接」とする角度をラジアンで返します。
#include <math.h>
double atan(double x); // 浮動小数点(double)版
float atanf(float x); // float版
long double atanl(long double x); // long double版戻り値の範囲は(-π/2, π/2)、つまり-90度から+90度の間です。
端点の±π/2は含まれません。
三角形でいうと、tanθ = 対辺 / 隣辺なので、atanを使えばθ = atan(対辺 / 隣辺)と書けます。
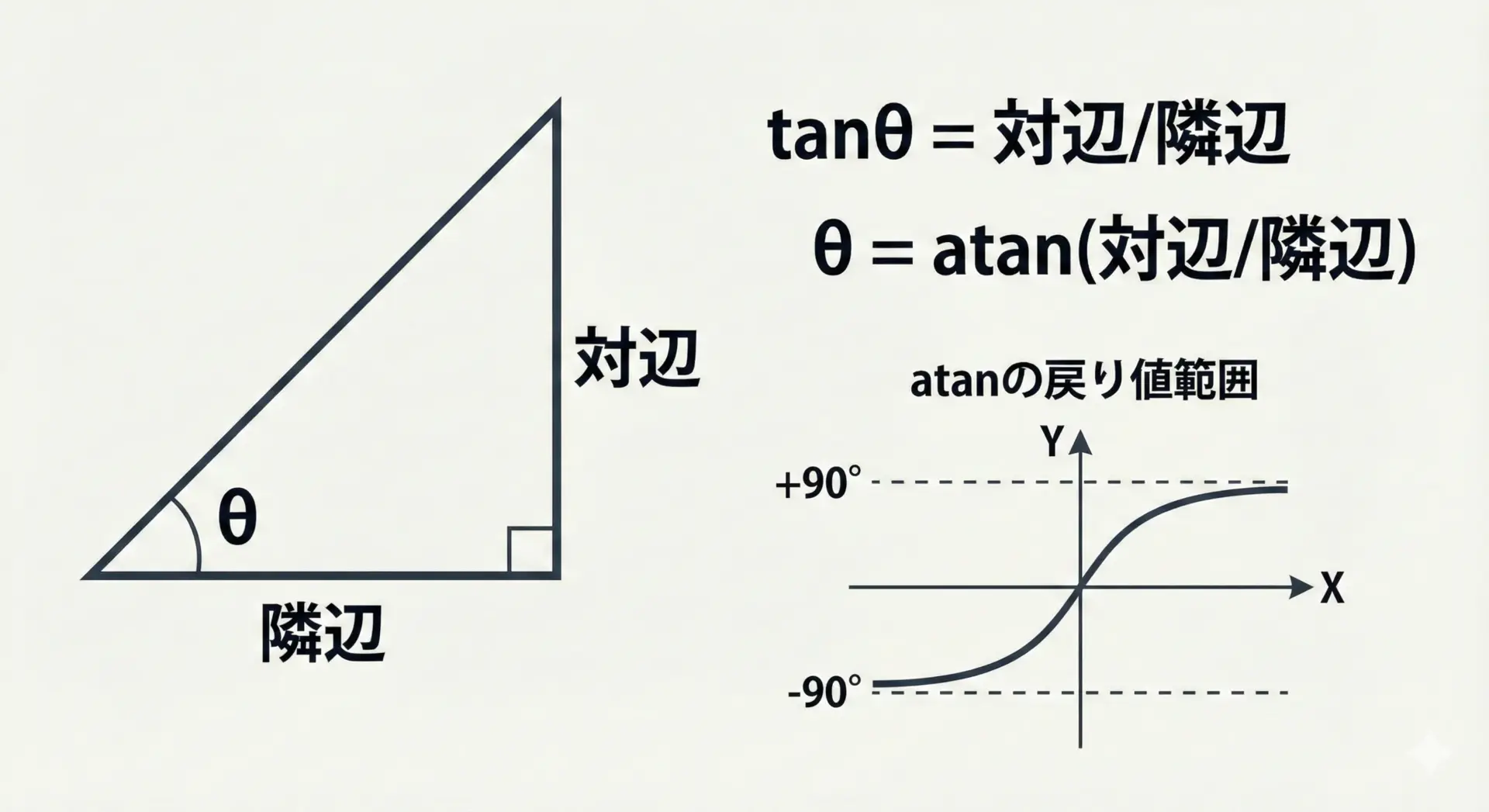
ただし、atanには象限の情報が失われるという問題があります。
例えばy/xの値だけからは、「x, yがともに正なのか、両方負なのか」を区別できません。
この問題を解決するために用意されているのが次のatan2です。
atan2関数で象限を考慮した角度を求める
atan2関数は、y座標とx座標の2つの値から角度を求める関数です。
書式は次のようになります。
#include <math.h>
double atan2(double y, double x); // 浮動小数点(double)版
float atan2f(float y, float x); // float版
long double atan2l(long double y, long double x); // long double版引数は順番に(y, x)である点に注意してください。
戻り値の範囲は(-π, π]、つまり-180度より大きく180度以下です。
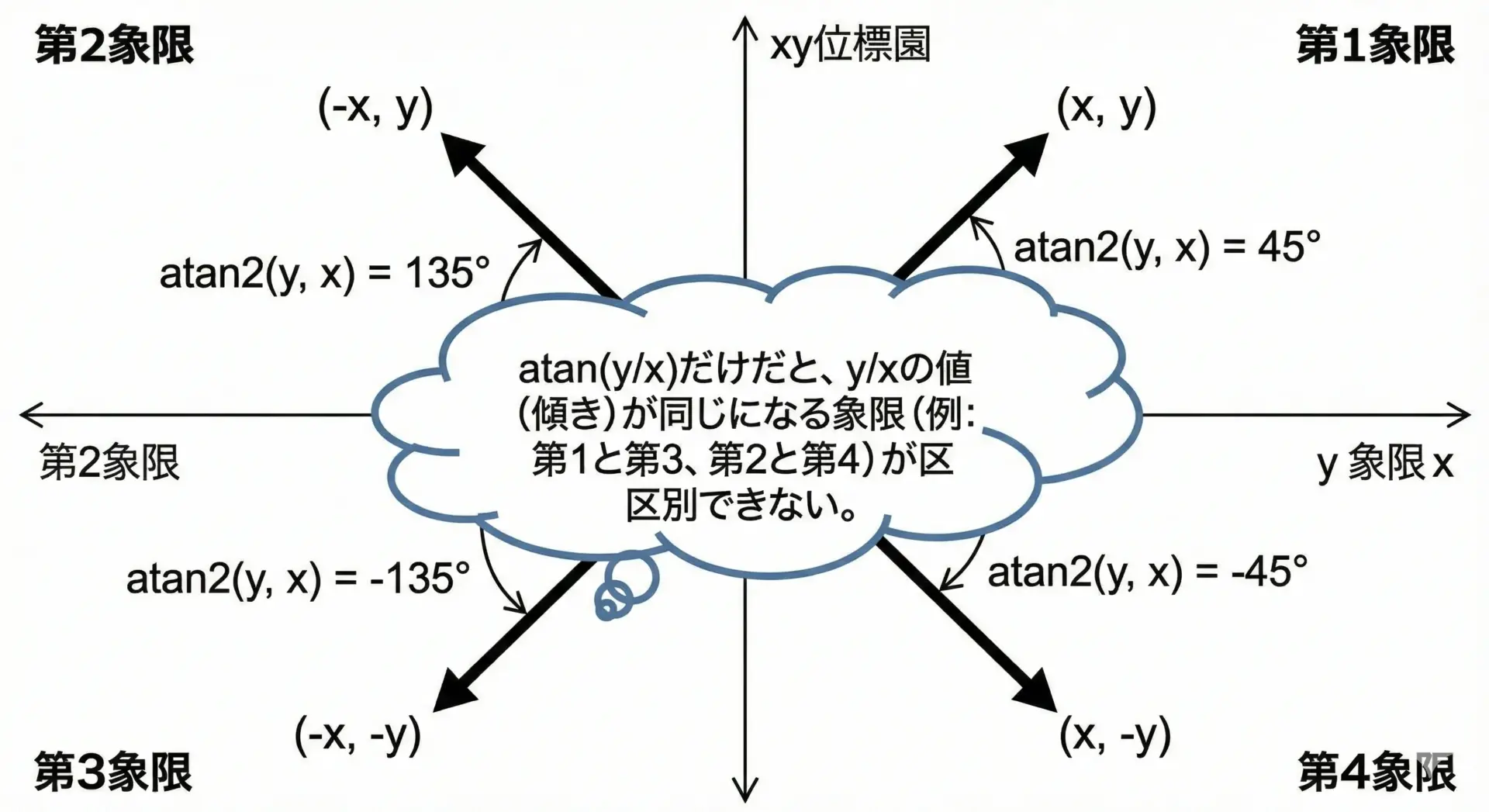
atan2は(x, y)の象限を考慮して正しい角度を返してくれるので、2D座標から角度を求めるときには基本的にatanではなくatan2を使います。
atan2を使った2D座標から角度を求める例
よくある例として、2Dゲームでプレイヤーから敵の方向を求めるケースを考えます。
- プレイヤー位置: (px, py)
- 敵位置: (ex, ey)
- プレイヤーから見た敵の方向ベクトル: (dx, dy) = (ex – px, ey – py)
このとき、プレイヤーから敵への角度θはatan2(dy, dx)で計算できます。
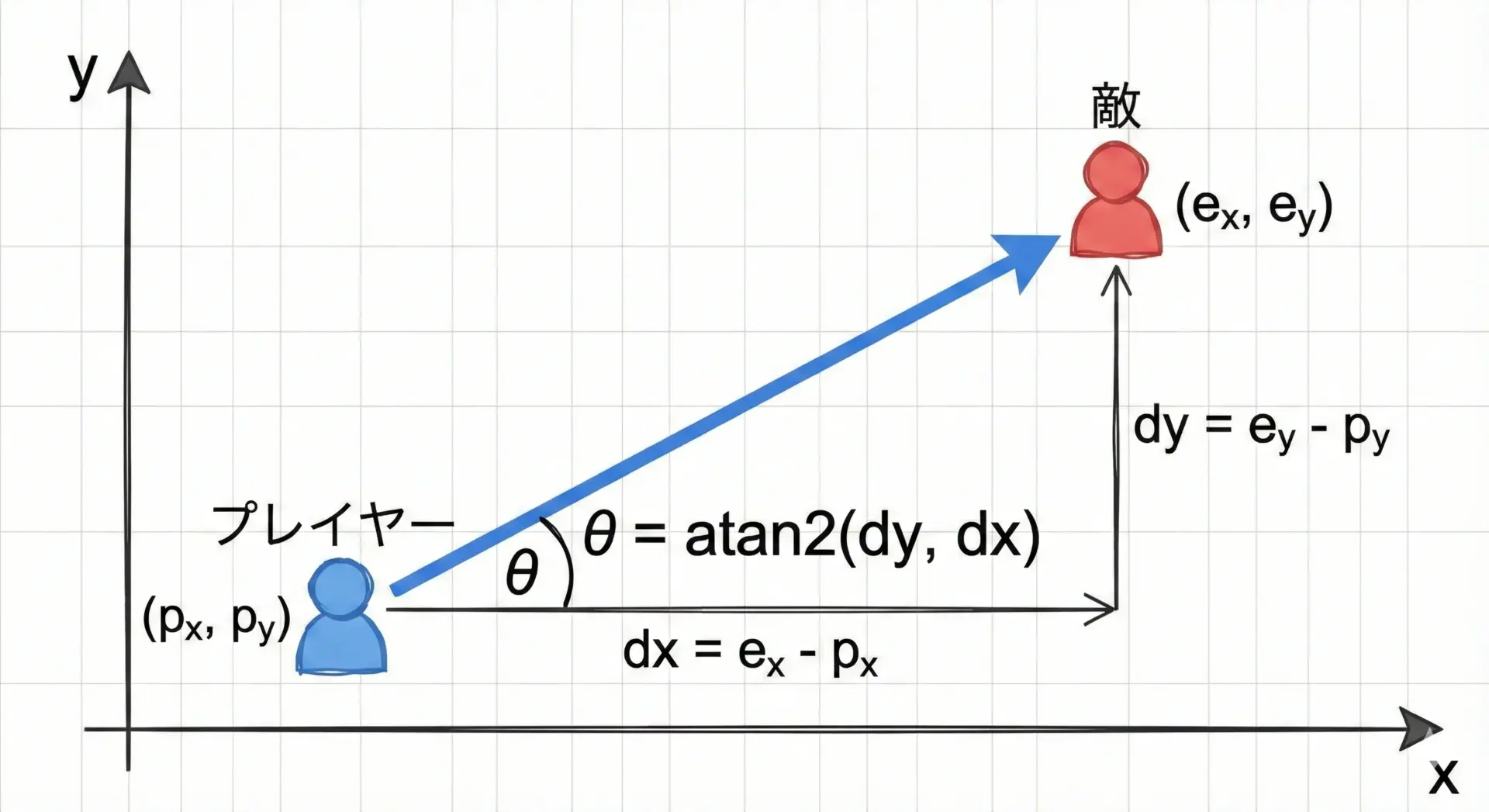
#include <stdio.h>
#include <math.h>
double rad2deg(double rad) {
return rad * 180.0 / M_PI;
}
int main(void) {
// プレイヤーと敵の座標
double px = 0.0, py = 0.0;
double ex = 3.0, ey = 4.0;
// プレイヤーから敵へのベクトル
double dx = ex - px;
double dy = ey - py;
// atan2で角度を求める (x軸正方向を0度とし、反時計回りに正)
double rad = atan2(dy, dx);
double deg = rad2deg(rad);
printf("player = (%.1f, %.1f)\n", px, py);
printf("enemy = (%.1f, %.1f)\n", ex, ey);
printf("d = (dx, dy) = (%.1f, %.1f)\n", dx, dy);
printf("θ = %.6f [rad]\n", rad);
printf("θ = %.6f [deg]\n", deg);
return 0;
}player = (0.0, 0.0)
enemy = (3.0, 4.0)
d = (dx, dy) = (3.0, 4.0)
θ = 0.927295 [rad]
θ = 53.130102 [deg]この例では、プレイヤーから見て敵は約53度の方向にいることが分かります。
角度の正規化(−π~π, 0~2π, 0~360度)の方法
atan2の戻り値は(-π, π]ですが、用途によっては次のような範囲に揃えたいことがよくあります。
- −π〜π の範囲
- 0〜2π の範囲
- 0〜360度 の範囲
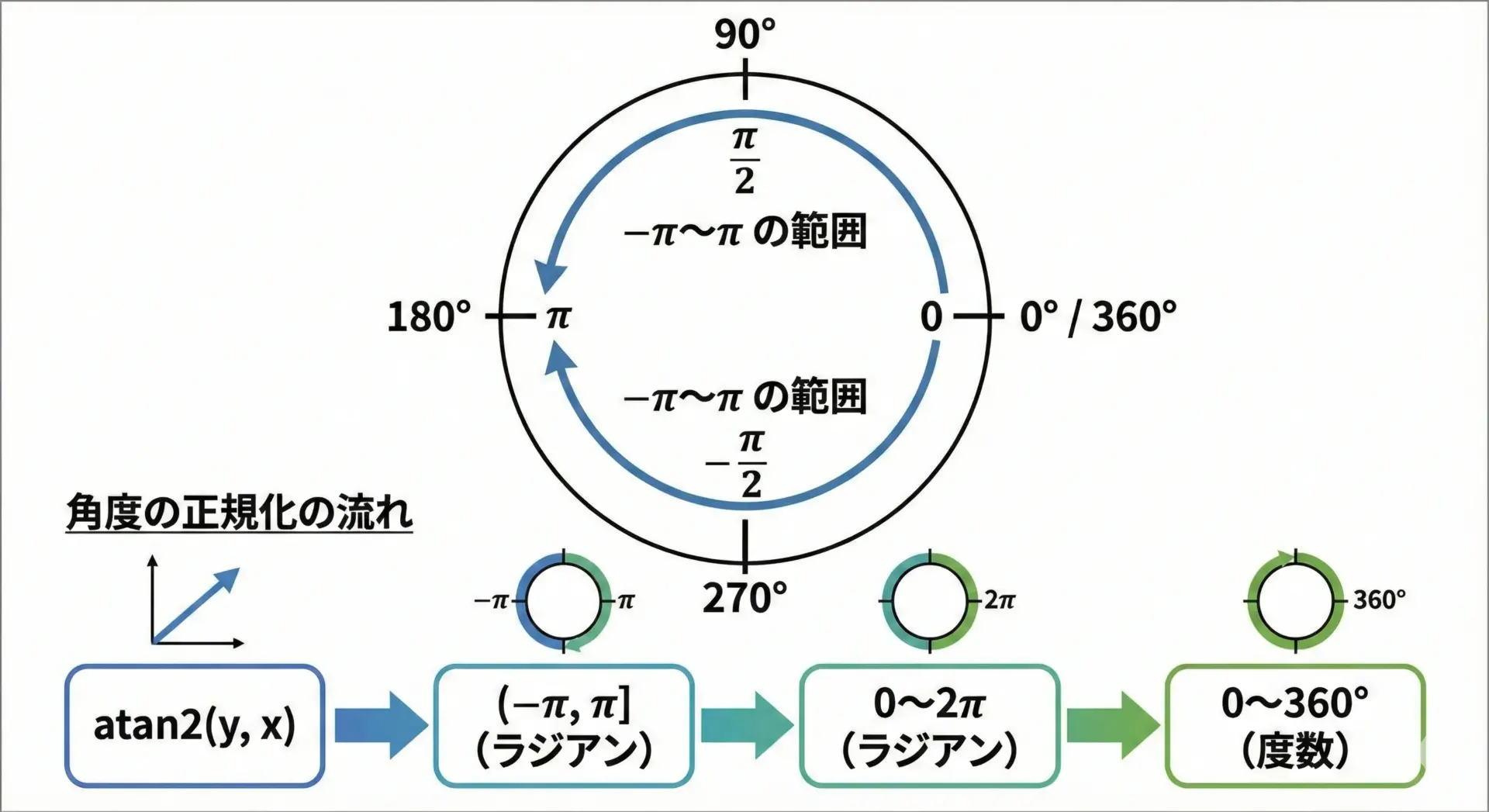
ここでは、角度を正規化する汎用的な関数をいくつか紹介します。
ラジアン角を −π〜π に正規化する
#include <math.h>
// 角度(ラジアン)を [-π, π) の範囲に正規化する
double normalize_rad_mpi_pi(double rad) {
// fmodで 2π の剰余を取る
rad = fmod(rad + M_PI, 2.0 * M_PI);
if (rad < 0.0) {
rad += 2.0 * M_PI;
}
return rad - M_PI;
}この関数は、入力がどのようなラジアン角でも必ず −π〜π の範囲に収まるように調整します。
ラジアン角を 0〜2π に正規化する
// 角度(ラジアン)を [0, 2π) の範囲に正規化する
double normalize_rad_0_2pi(double rad) {
rad = fmod(rad, 2.0 * M_PI);
if (rad < 0.0) {
rad += 2.0 * M_PI;
}
return rad;
}例えば、-π/2はこの関数を通すと3π/2になります。
度数法の角度を 0〜360度 に正規化する
#include <math.h>
// 角度(度)を [0, 360) の範囲に正規化する
double normalize_deg_0_360(double deg) {
deg = fmod(deg, 360.0);
if (deg < 0.0) {
deg += 360.0;
}
return deg;
}これらの関数を使うと、負の角度や360度を超える角度を扱うときにも一貫した表現が得られます。
例えば、atan2の結果を常に0〜360度で表現したい場合は次のようにします。
#include <stdio.h>
#include <math.h>
double rad2deg(double rad) {
return rad * 180.0 / M_PI;
}
double normalize_deg_0_360(double deg) {
deg = fmod(deg, 360.0);
if (deg < 0.0) {
deg += 360.0;
}
return deg;
}
int main(void) {
double rad = atan2(-1.0, -1.0); // 第3象限
double deg = rad2deg(rad);
double norm_deg = normalize_deg_0_360(deg);
printf("atan2(-1, -1) = %.6f [rad]\n", rad);
printf("deg = %.6f [deg]\n", deg);
printf("norm_deg = %.6f [deg]\n", norm_deg);
return 0;
}atan2(-1, -1) = -2.356194 [rad]
deg = -135.000000 [deg]
norm_deg = 225.000000 [deg]このように、座標から得た角度を用途に適した範囲に変換することで、プログラムのロジックがシンプルになり、バグも減らせます。
まとめ
本記事では、C言語における逆三角関数 asin/acos/atan/atan2 の基本と実用的な使い方を解説しました。
asinとacosはそれぞれ正弦・余弦の逆で、引数範囲は共に−1〜1、戻り値の範囲が異なること、acosが特にベクトル間の角度計算で有用であることを確認しました。
また、atanは単純なtanの逆、atan2は2次元座標から象限を考慮して角度を求める関数であり、角度の正規化(−π〜π, 0〜2π, 0〜360度)やラジアン・度の変換を組み合わせることで、座標処理やゲーム、物理シミュレーションなど幅広い場面で安全かつ直感的に角度を扱えるようになります。
これらのポイントを押さえておけば、C言語で角度を使うプログラムの土台をしっかりと構築できます。