C言語でゲーム開発や物理シミュレーション、グラフ描画を行うとき、避けて通れないのが三角関数です。
本記事ではC言語標準ライブラリのsin/cos/tanの使い方から、度数法とラジアンの変換、波形生成や角度計算まで、実用的な観点で丁寧に解説します。
初学者でも理解しやすいように図解イメージやサンプルコードを交えながら説明していきます。
三角関数の基本
まずは、C言語で三角関数を使うときの前提知識や、「どのヘッダをインクルードすればいいのか」「引数と戻り値は何型なのか」といった基本から確認していきます。
三角関数を使うには
C言語で三角関数を使用するには、標準ライブラリmath.hをインクルードします。
多くの環境(特にLinux系)では、リンク時に-lmオプションが必要となる点にも注意します。
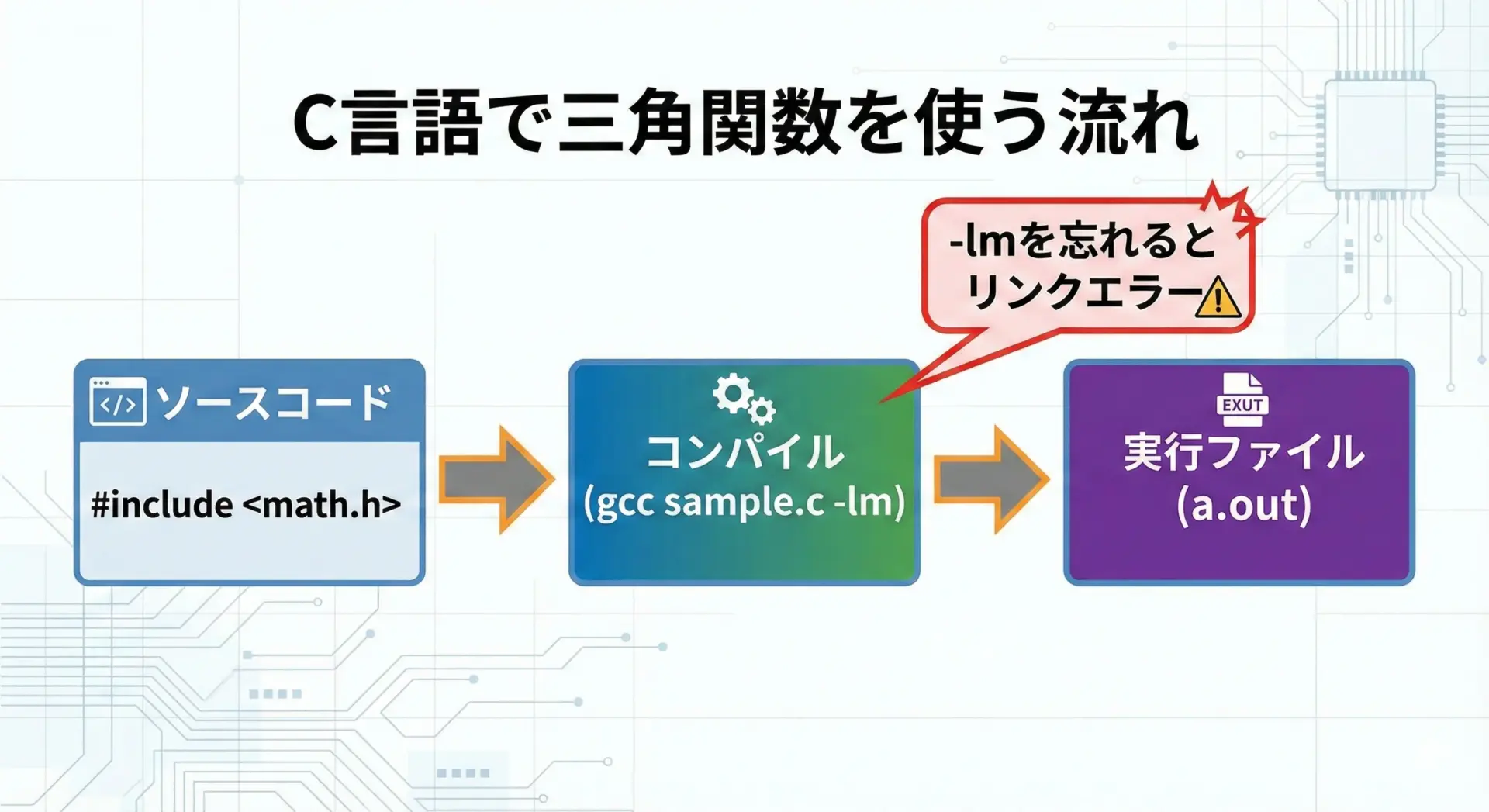
math.hをインクルードする
三角関数sin/cos/tanはいずれもmath.hに宣言されています。
そのため、関数を使うファイルで次のようにインクルードします。
#include <stdio.h>
#include <math.h> // 三角関数やsqrtなどの数学関数を宣言
int main(void) {
double x = 0.5;
double y = sin(x); // sin関数を利用
printf("sin(%f) = %f\n", x, y);
return 0;
}sin(0.500000) = 0.479426多くのコンパイラでは、次のようにコンパイルします。
gcc main.c -o main -lm特にLinuxやUnix系の環境では、-lmを付け忘れるとリンクエラーになります。
Windows(Visual Studioなど)では通常は不要ですが、環境ごとの差として覚えておくと良いです。
sin cos tan関数の戻り値と引数の型
C言語の三角関数には倍精度(double)版だけでなく、単精度(float)版、long double版があります。
代表的なプロトタイプは次のようになっています。
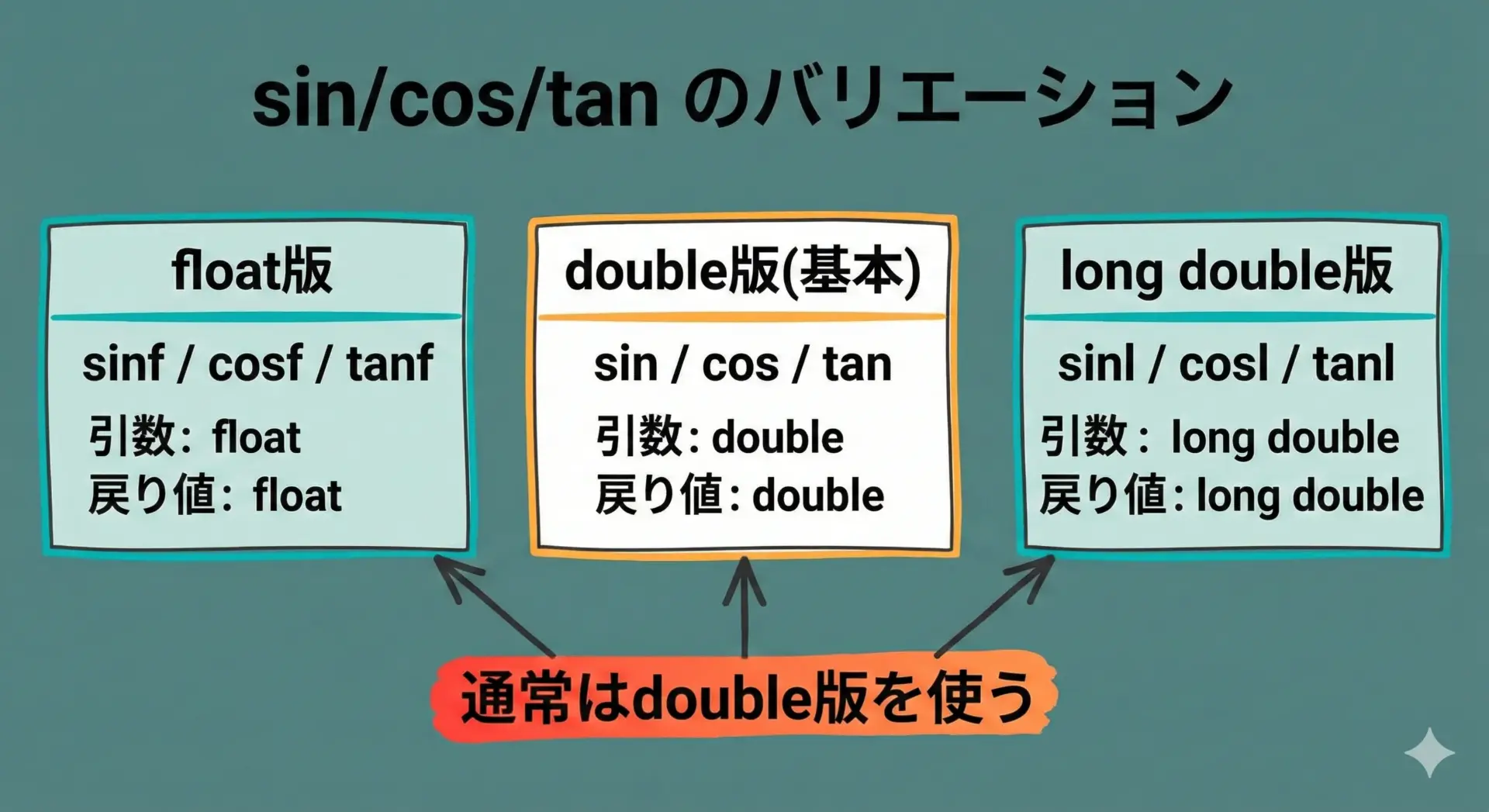
代表的なプロトタイプ
C言語(厳密にはC標準)では、次のように宣言されています(概念図です)。
/* 倍精度版(最もよく使う) */
double sin(double x);
double cos(double x);
double tan(double x);
/* 単精度版 */
float sinf(float x);
float cosf(float x);
float tanf(float x);
/* long double版 */
long double sinl(long double x);
long double cosl(long double x);
long double tanl(long double x);通常の開発ではdouble版を使うのが基本です。
理由としては、精度と速度のバランスが良く、多くのサンプルコードや他言語でもdouble相当を基準としているためです。
型の自動変換に注意
例えば、floatの変数にsin(double版)をそのまま適用することは可能ですが、その場合は一度doubleに拡張されて計算された後、結果がfloatに丸められます。
#include <stdio.h>
#include <math.h>
int main(void) {
float xf = 0.5f;
float yf = sin(xf); // sin(float) ではなく sin(double) が呼ばれる
float yf_exact = sinf(xf); // こちらはfloat版
printf("yf (sin) = %.10f\n", yf);
printf("yf (sinf) = %.10f\n", yf_exact);
return 0;
}出力例(値は環境により微妙に異なります):
yf (sin) = 0.4794255495
yf (sinf) = 0.4794255495多くの環境では実用上同じに見えますが、厳密に型をそろえたい場合や性能チューニング時にはsinf/cosf/tanfのように接尾辞f付きの関数を使います。
sin cos tan以外の関連関数
三角関数まわりには、逆三角関数や双曲線関数、直角三角形の斜辺を求める関数など、多数の関連関数があります。
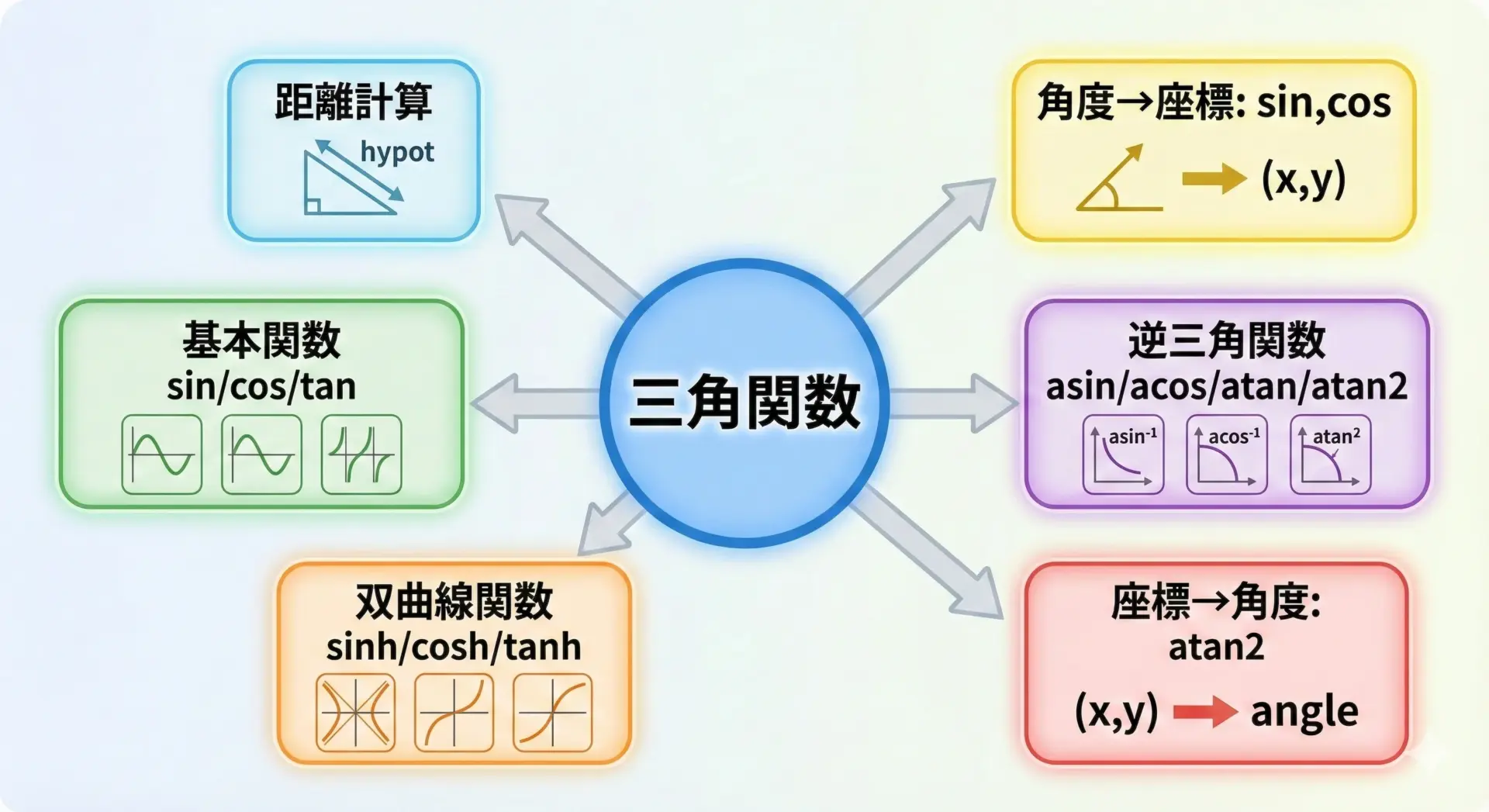
主な関連関数一覧
代表的な関数を表にまとめます。
| 分類 | 関数名 | 説明 |
|---|---|---|
| 逆三角関数 | asin, acos, atan, atan2 | sin/cos/tanの逆。角度(ラジアン)を求める |
| 双曲線関数 | sinh, cosh, tanh | 数値計算や物理モデリングで利用 |
| 逆双曲線関数 | asinh, acosh, atanh | 双曲線関数の逆 |
| 距離・ノルム | hypot | sqrt(xx + yy)と同等(安定・安全版) |
特にatan2とhypotは、2次元ベクトルの角度や長さを求める際に非常に便利です。
これらは後半の「2点の座標から角度を求める」「ベクトルの向きや回転角の計算」で詳しく扱います。
度数法とラジアン変換の基礎
C言語の三角関数はすべて「ラジアン(rad)」単位で角度を扱います。
一方、人間が普段使うのはほとんどが「度数法(deg)」です。
そのギャップを埋めるために、度数法とラジアンの変換をしっかり理解しておくことが重要です。
角度をラジアンに変換する方法
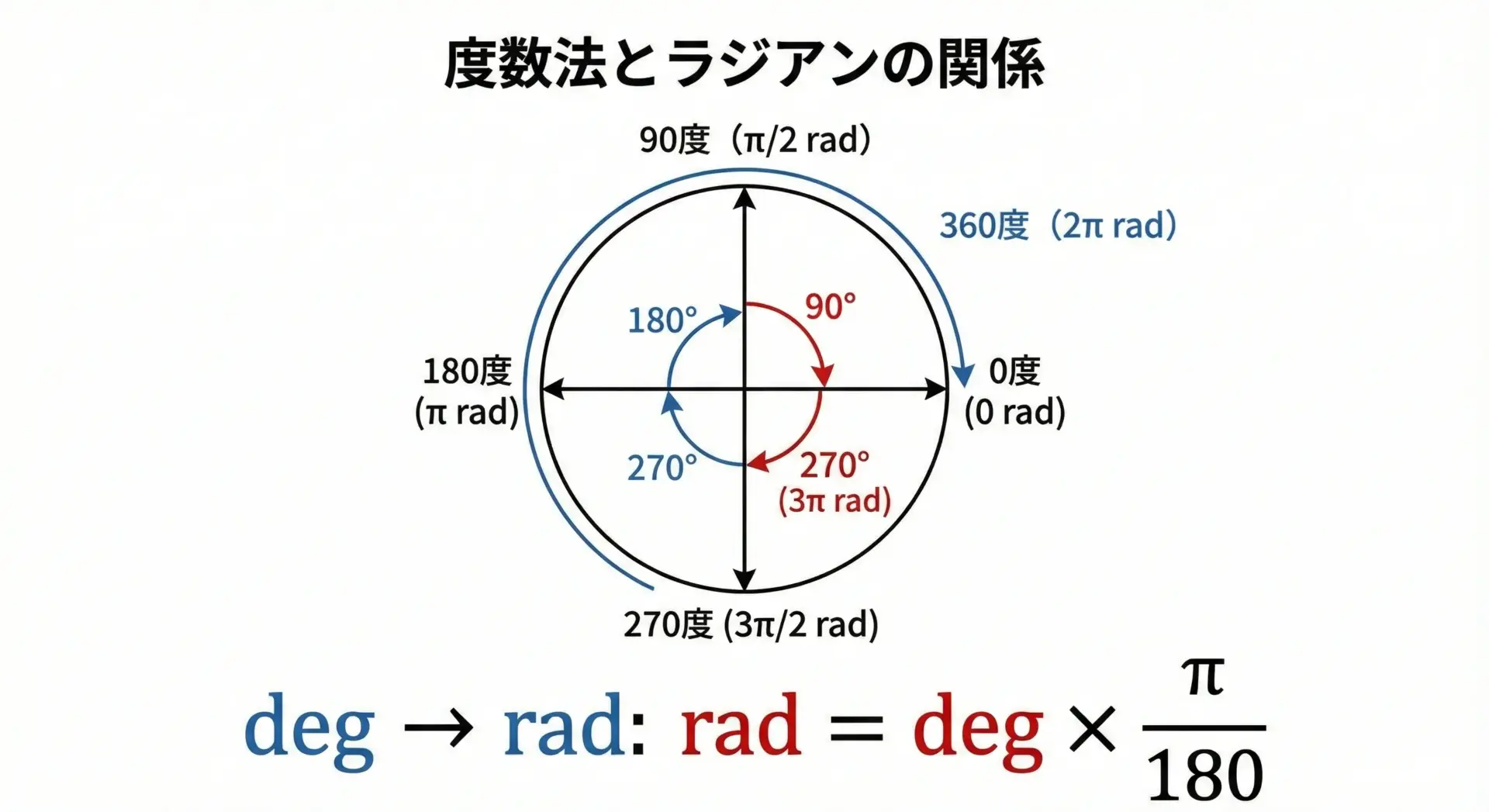
度数法(度)からラジアン(rad)への変換式は次の通りです。
rad = deg × π / 180
ここでπは円周率(約3.14159265…)です。
C言語で関数に渡すときは、この式を用いて変換します。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846 // 自作の円周率定数
/* 度数法(deg)からラジアン(rad)へ変換する関数 */
double deg2rad(double deg) {
return deg * (MY_PI / 180.0);
}
int main(void) {
double deg = 30.0;
double rad = deg2rad(deg);
double s = sin(rad); // 30度のsin値
printf("deg = %f, rad = %f, sin(30deg) = %f\n", deg, rad, s);
return 0;
}deg = 30.000000, rad = 0.523599, sin(30deg) = 0.500000sin(30度)は0.5になることは有名ですが、ラジアンに変換しないと正しく計算されないことに注意します。
30という値をそのままsinに渡してしまうと、30ラジアン(約1718度)として計算されてしまいます。
ラジアンを度数法に変換する方法
逆に、計算結果として得られたラジアンを度数法に直したい場合もよくあります。
グラフ表示やデバッグ用のログなど、人間が直感的に理解したい場面です。
ラジアンから度数法への変換式は次の通りです。
deg = rad × 180 / π
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
/* ラジアン(rad)から度数法(deg)へ変換する関数 */
double rad2deg(double rad) {
return rad * (180.0 / MY_PI);
}
int main(void) {
double rad = MY_PI / 3.0; // 60度に相当
double deg = rad2deg(rad);
printf("rad = %f, deg = %f\n", rad, deg);
return 0;
}rad = 1.047198, deg = 60.000000角度を扱う関数(例えばatanやatan2)はラジアンで結果を返すため、ログ表示やUIで度数を使いたいときはrad2degを通す、といったパターンが定番です。
円周率M_PIと自作のPI定数の扱い方
環境によってはmath.hでM_PIが定義されている場合がありますが、C標準規格では必須ではありません。
そのため、自前で定義するか、環境依存マクロをうまく扱う必要があります。
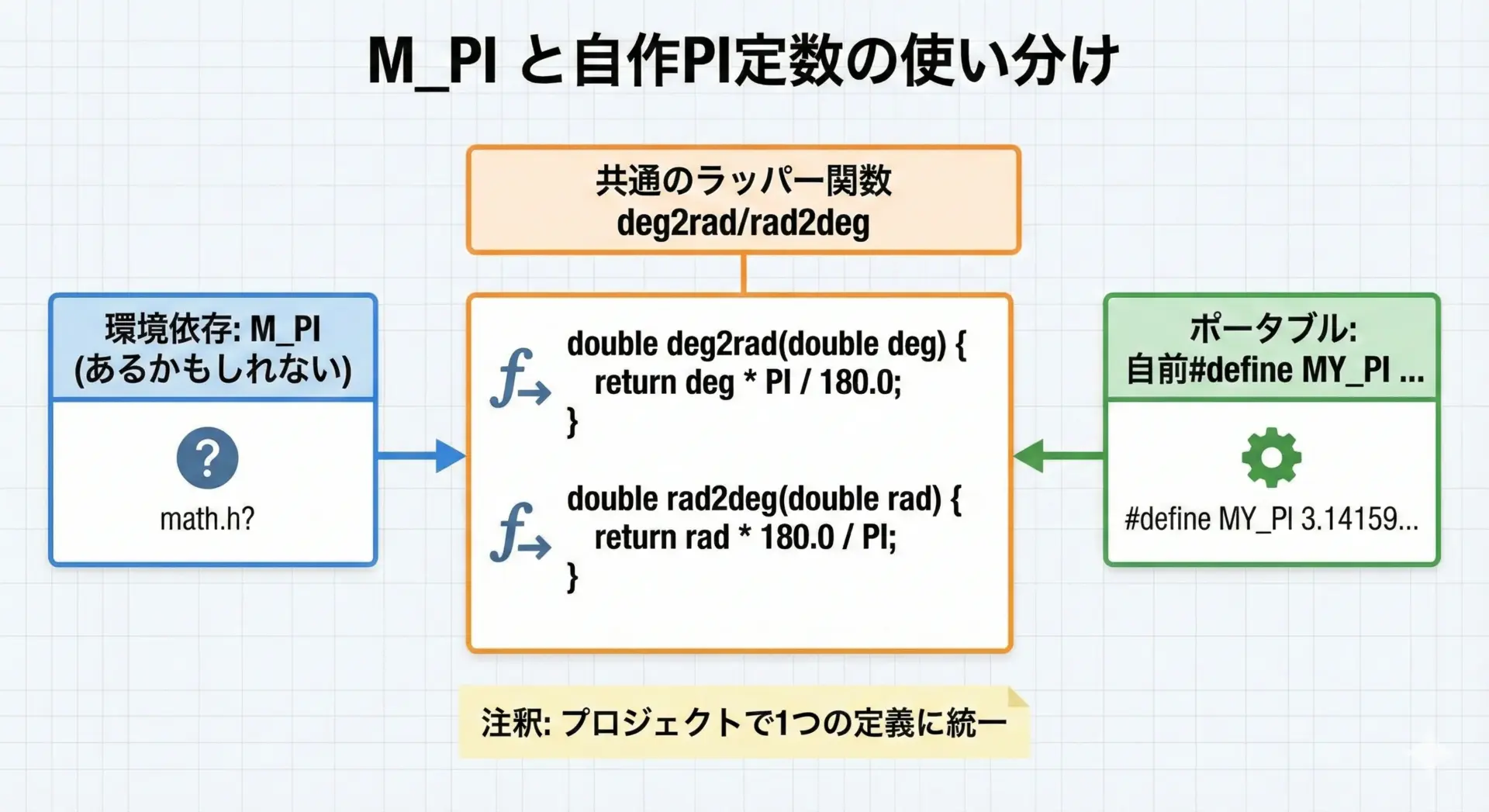
M_PIの有無を気にしないための書き方
最も安全なのは、プロジェクト内で自前の定数を定義してしまうことです。
例えば次のように書いておくと、どの環境でも同じように動きます。
#include <stdio.h>
#include <math.h>
/* 円周率定数を自前で定義 (double精度) */
#ifndef MY_PI
#define MY_PI 3.14159265358979323846
#endif
double deg2rad(double deg) {
return deg * (MY_PI / 180.0);
}
double rad2deg(double rad) {
return rad * (180.0 / MY_PI);
}
int main(void) {
printf("PI = %.20f\n", MY_PI);
return 0;
}PI = 3.14159265358979311600プロジェクト全体で使う円周率は原則として1つに統一し、ヘッダファイルなどにまとめておくと、精度や値の不一致による微妙な誤差を減らせます。
度数とラジアンの混在によるバグ防止テクニック
度数とラジアンを混在させると、非常に分かりにくいバグが発生します。
特に変数名やコメントで単位を明示しておくことが重要です。
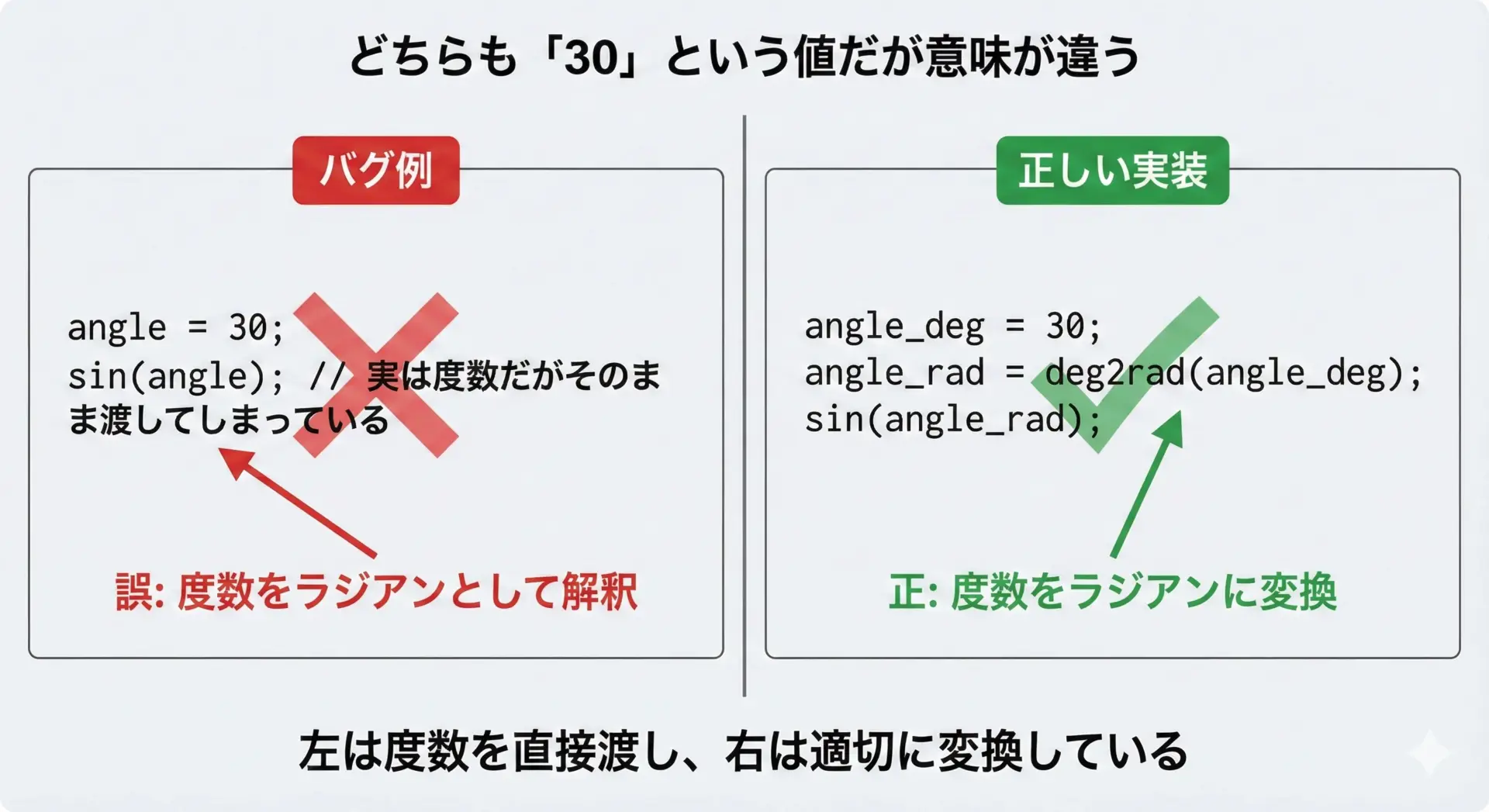
単位を変数名で表現する
次のように、変数名に_degや_radといった接尾辞を必ず付けると、単位の取り違えをかなり防げます。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
double deg2rad(double deg) {
return deg * (MY_PI / 180.0);
}
int main(void) {
double angle_deg = 45.0; // 度数法で45度
double angle_rad = deg2rad(angle_deg); // ラジアンに変換
double s = sin(angle_rad);
printf("angle_deg = %f, angle_rad = %f, sin = %f\n",
angle_deg, angle_rad, s);
return 0;
}また、関数の引数名にも単位を含めておくと読みやすくなります。
例えばrotate_deg(double angle_deg)のようにすると、その関数が度数法を受け取ることが明示されます。
sin cos tanでできる波形生成と角度計算
三角関数は周期的な波形生成や座標から角度を求める幾何計算など、実用的な用途が非常に多いです。
この章では、具体的なサンプルコードとともに、よくあるパターンを見ていきます。
sin関数で正弦波を生成する方法
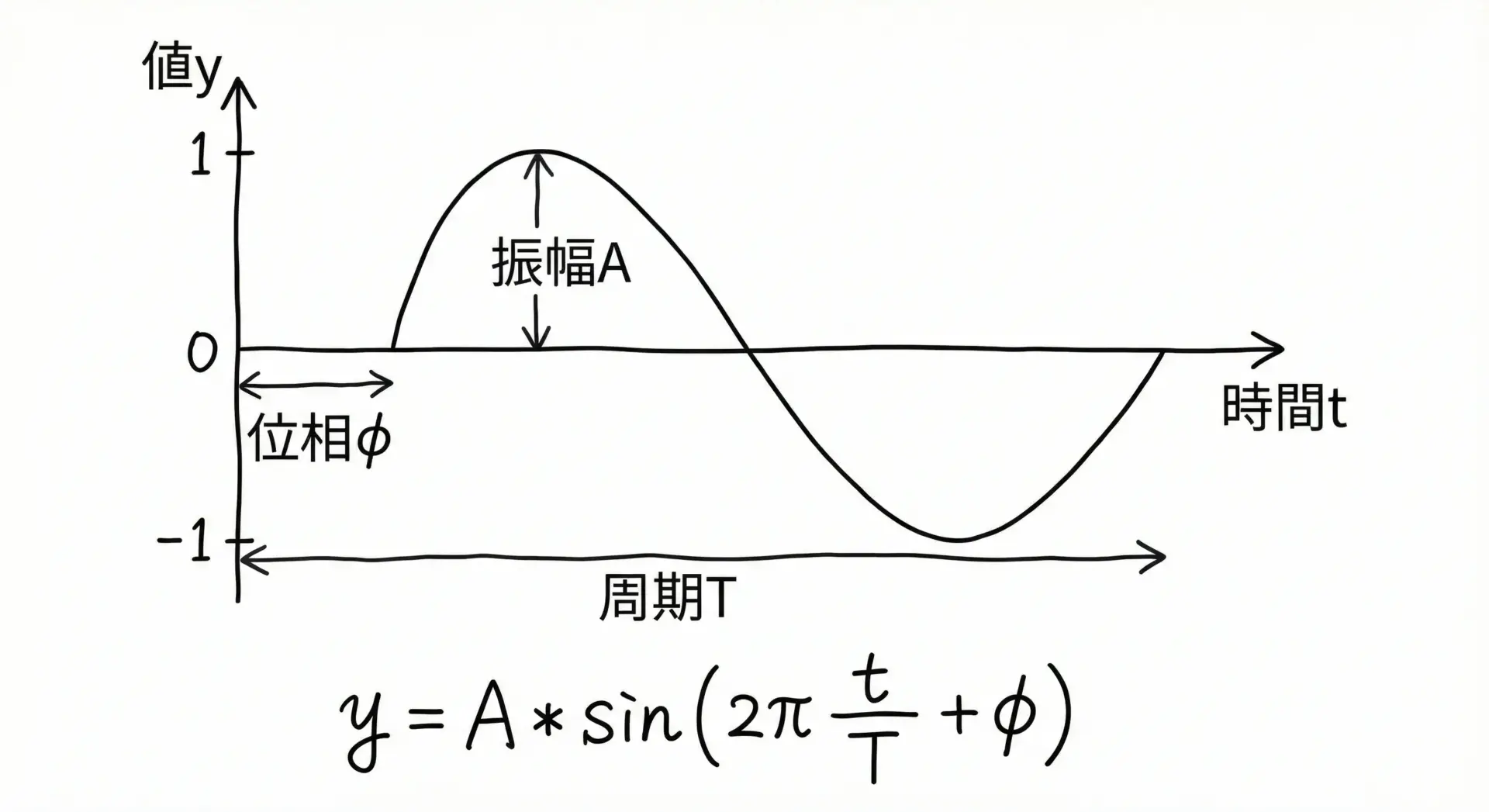
正弦波は、時間や角度に対して周期的に変化する波形です。
一般的な形は次の式で表されます。
y = A × sin(2π × t / T + φ)
ここで、Aは振幅、Tは周期、φは位相です。
C言語で単純な正弦波をサンプリングして表示する例を見てみましょう。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
int main(void) {
double A = 1.0; // 振幅
double T = 2.0; // 周期(ここでは2秒を1周期と仮定)
double dt = 0.1; // サンプリング間隔
double t;
printf("t, sin_wave\n");
for (t = 0.0; t <= 2.0 * T; t += dt) {
double rad = 2.0 * MY_PI * t / T; // 角度(ラジアン)
double y = A * sin(rad); // 正弦波の値
printf("%6.2f, % .6f\n", t, y);
}
return 0;
}出力例(一部):
t, sin_wave
0.00, 0.000000
0.10, 0.309017
0.20, 0.587785
0.30, 0.809017
0.40, 0.951057
...このようにして得られた値を、グラフ描画ライブラリやゲームの座標更新処理に使うことで、滑らかに揺れるアニメーションや周期運動を簡単に実現できます。
cos関数で位相の違う波形を作る
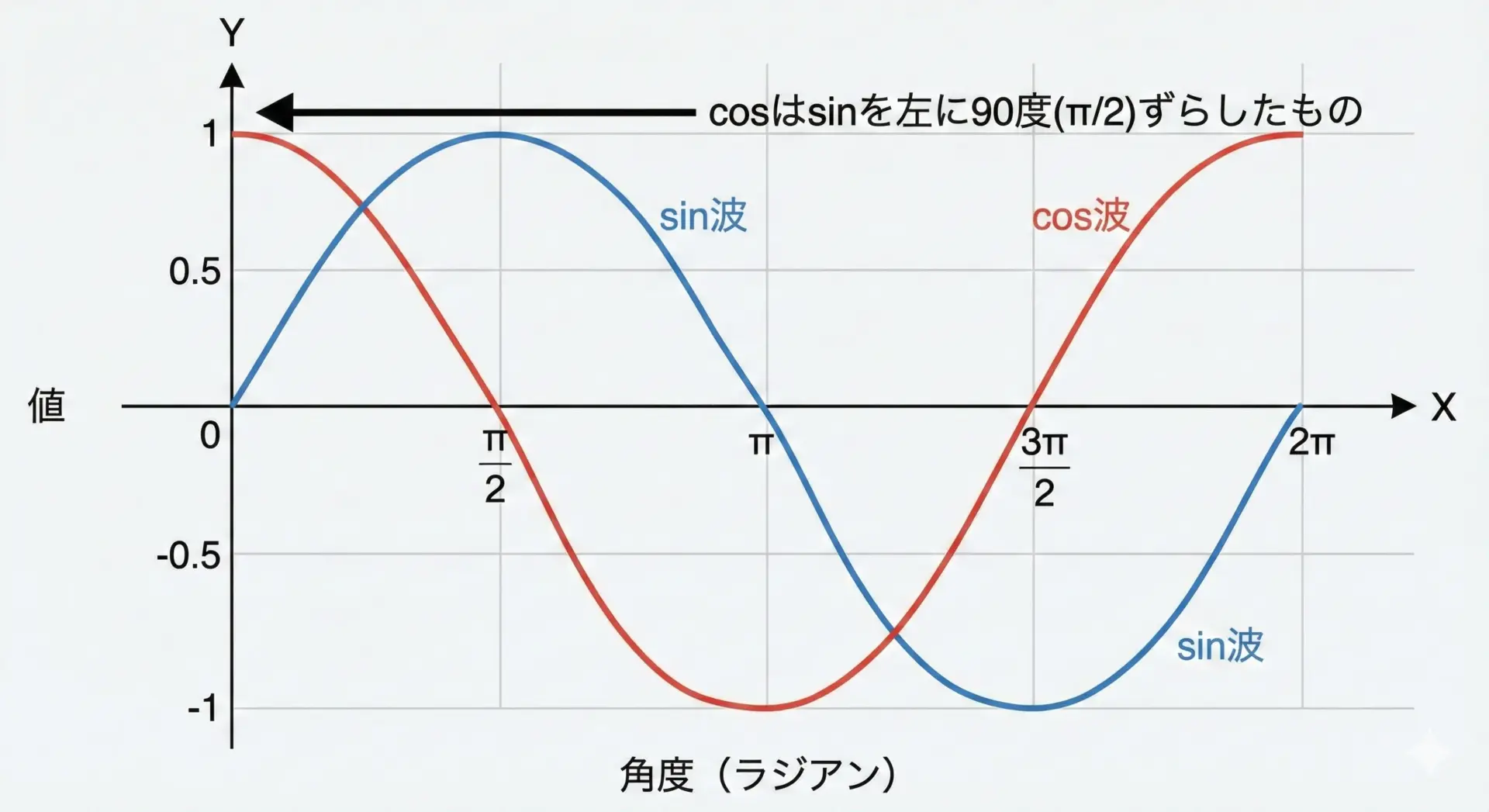
cos関数はsin関数とよく似ていますが、位相が90度(π/2)だけずれています。
数学的にはcos(x) = sin(x + π/2)です。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
int main(void) {
double dt = MY_PI / 8.0; // サンプリングステップ
double x;
printf("x(rad), sin(x), cos(x)\n");
for (x = 0.0; x <= 2.0 * MY_PI + 1e-9; x += dt) {
double s = sin(x);
double c = cos(x);
printf("%6.3f, % .6f, % .6f\n", x, s, c);
}
return 0;
}出力例(一部):
x(rad), sin(x), cos(x)
0.000, 0.000000, 1.000000
0.393, 0.382684, 0.923880
0.785, 0.707107, 0.707107
1.178, 0.923880, 0.382684
1.571, 1.000000, 0.000000
...この位相差を利用すると、2次元の円運動を簡単に表現できます。
例えば中心(cx, cy)、半径Rの円の上を動く点の座標(x, y)は、次のように表せます。
double angle_rad = ...; // 角度(ラジアン)
double x = cx + R * cos(angle_rad);
double y = cy + R * sin(angle_rad);このように、cosがx座標、sinがy座標という組み合わせは非常によく使われます。
tan関数の特徴とグラフの発散に注意するポイント
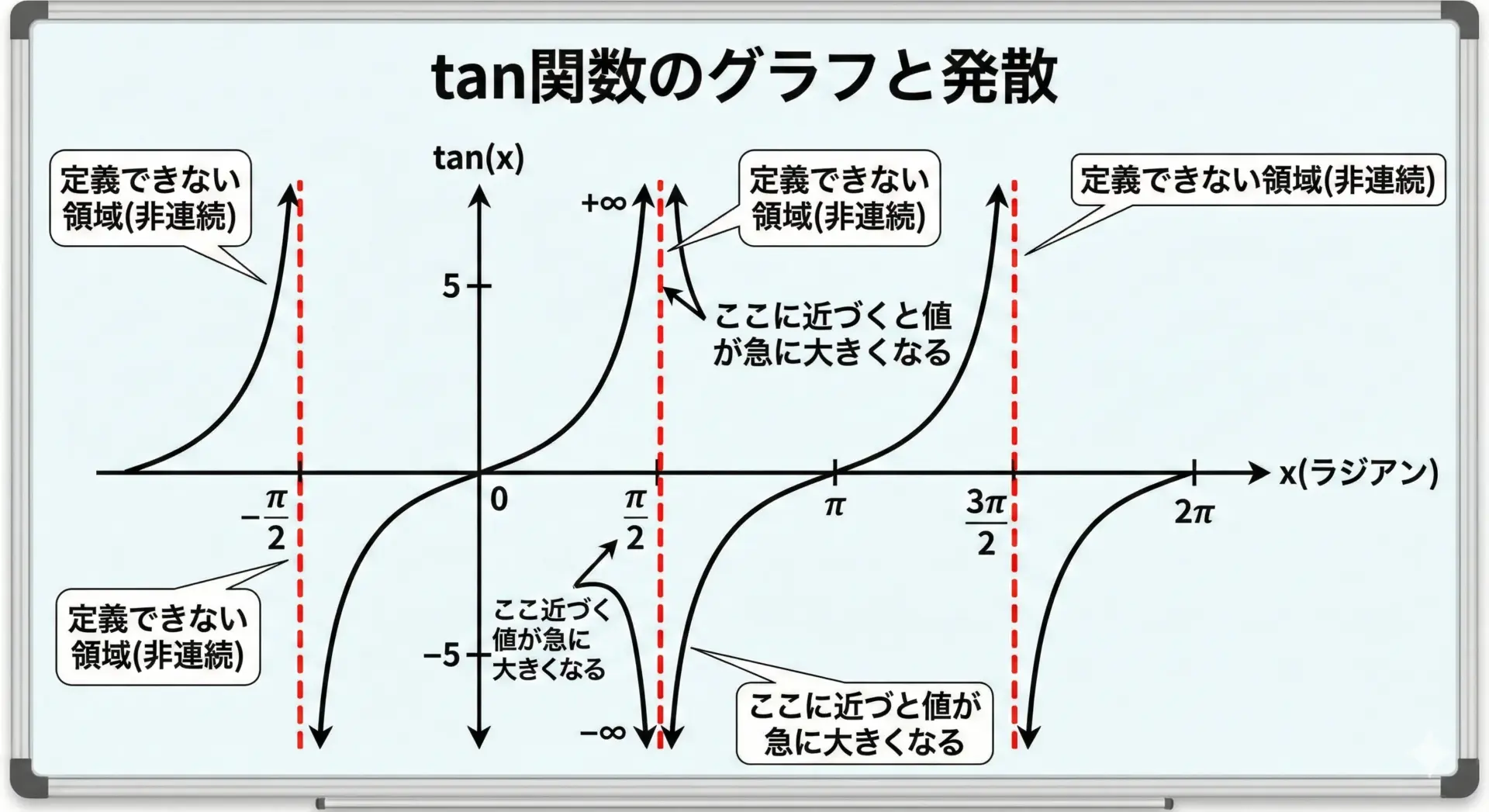
tan関数はsin(x)/cos(x)の比として定義されます。
そのため、cos(x)が0になる点(±π/2, ±3π/2, …)では、値が正負の無限大に発散します。
実装上の注意点として、cos(x)が非常に小さい値になる近辺では、tan(x)は極端に大きな値を返します。
これは浮動小数点の範囲を超える場合もあり、不安定さの原因になります。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
int main(void) {
double x_values[] = {
MY_PI / 4.0, // 45度
MY_PI / 3.0, // 60度
MY_PI / 2.0 - 1e-6, // 90度の手前
MY_PI / 2.0, // 90度 (理論上は無限大)
};
int n = sizeof(x_values) / sizeof(x_values[0]);
for (int i = 0; i < n; ++i) {
double x = x_values[i];
double t = tan(x);
printf("x = %.10f rad, tan(x) = %.10f\n", x, t);
}
return 0;
}出力例(一部、環境により異なる):
x = 0.7853981634 rad, tan(x) = 1.0000000000
x = 1.0471975512 rad, tan(x) = 1.7320508076
x = 1.5707956536 rad, tan(x) = 999999.9999932530
x = 1.5707963268 rad, tan(x) = -22877332.595004845590度ちょうど付近では、非常に大きな値になったり、符号が反転したりと、直感とずれた動作をすることがあります。
そのため、tanを使った計算では、角度がこの危険領域に近づかないよう制約を設けるなどの工夫が必要です。
2点の座標から角度を求める
2次元平面上の2点(x1, y1)と(x2, y2)が与えられたとき、ベクトル(x2 – x1, y2 – y1)がどの方向(角度)を向いているかを知りたい場面はよくあります。
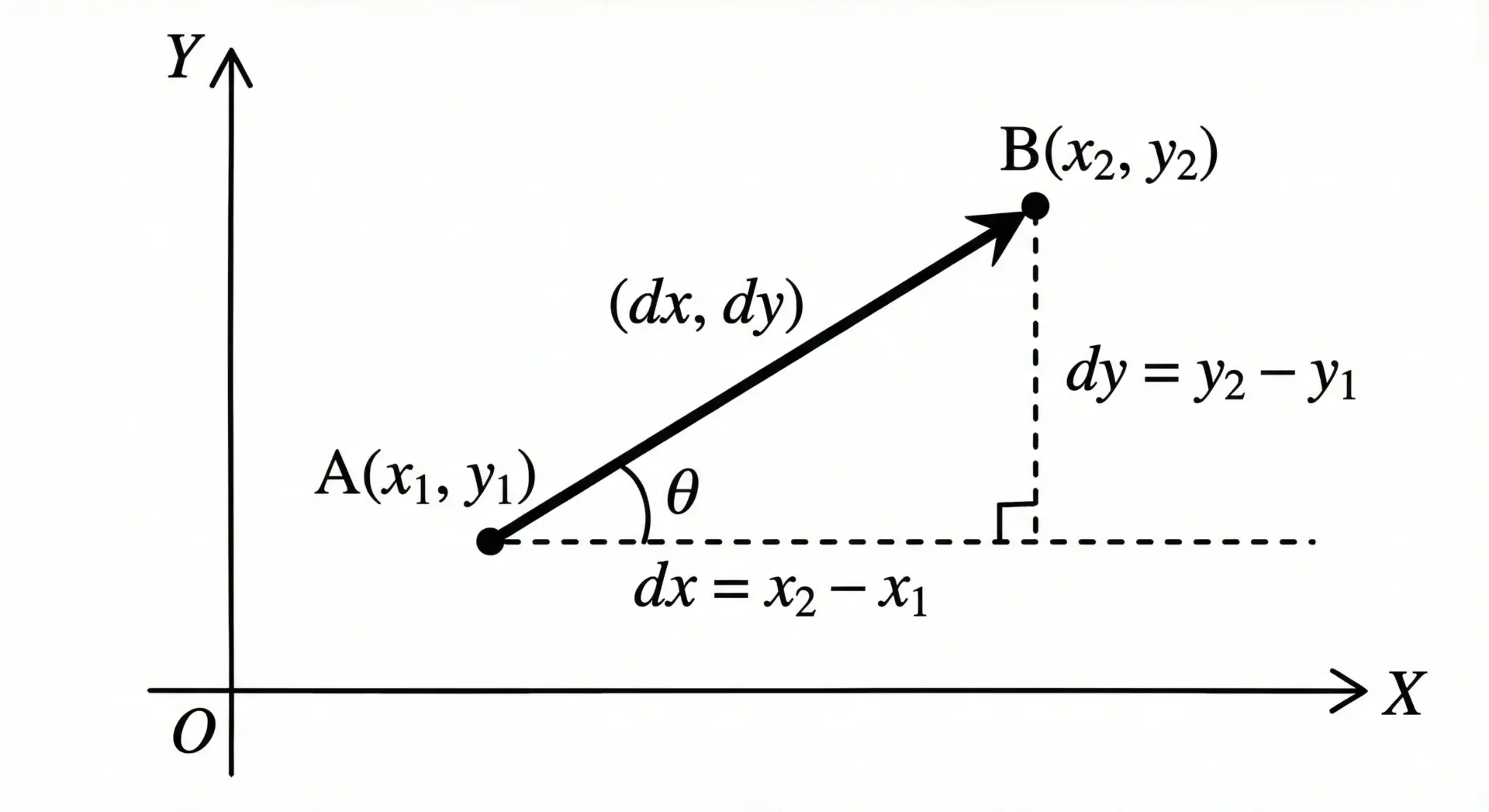
このとき便利なのがatan2関数です。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
double rad2deg(double rad) {
return rad * (180.0 / MY_PI);
}
int main(void) {
double x1 = 0.0, y1 = 0.0; // 基準点
double x2 = 1.0, y2 = 1.0; // 目標点(第1象限)
double dx = x2 - x1;
double dy = y2 - y1;
// atan2(y, x): ベクトル(x, y)の角度(ラジアン)を返す
double angle_rad = atan2(dy, dx);
double angle_deg = rad2deg(angle_rad);
printf("dx = %f, dy = %f\n", dx, dy);
printf("angle = %f rad (=%f deg)\n", angle_rad, angle_deg);
return 0;
}dx = 1.000000, dy = 1.000000
angle = 0.785398 rad (=45.000000 deg)atan2は、dyとdxの符号を見て、どの象限かを判断してくれます。
そのため、単純なatan(dy/dx)と違って、xが0に近い場合でも安全に扱えます。
ベクトルの向きや回転角の計算に三角関数を使う
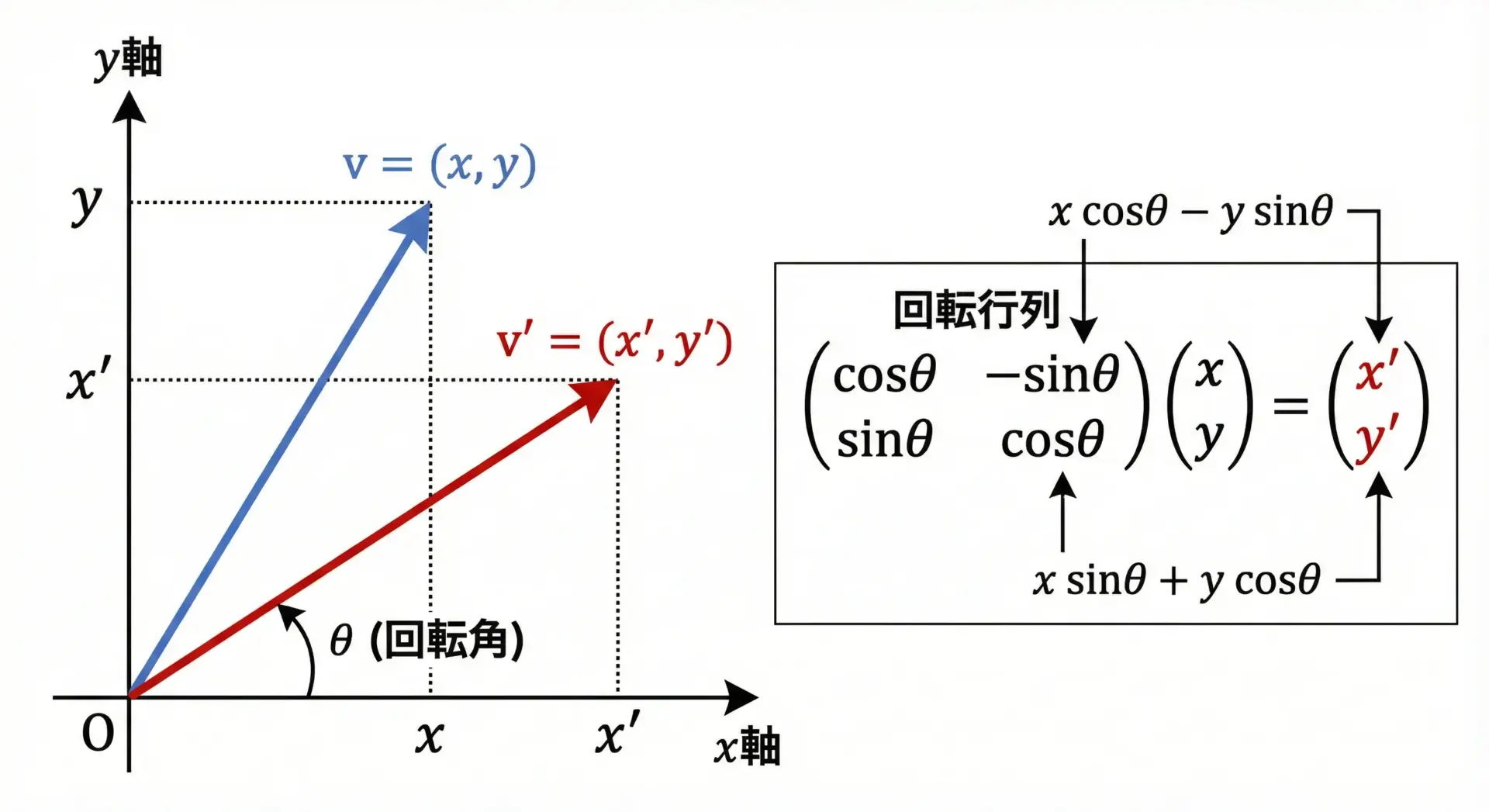
2Dベクトル(x, y)を角度θだけ回転させる場合、回転行列を用いるのが一般的です。
x’ = x × cosθ – y × sinθ y’ = x × sinθ + y × cosθ
これをC言語で関数化してみます。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
double deg2rad(double deg) {
return deg * (MY_PI / 180.0);
}
/* 2Dベクトル(x, y)をdeg度だけ回転させる関数 */
void rotate_vec2(double x, double y, double deg,
double *out_x, double *out_y) {
double rad = deg2rad(deg);
double c = cos(rad);
double s = sin(rad);
// 回転行列との積
*out_x = x * c - y * s;
*out_y = x * s + y * c;
}
int main(void) {
double x = 1.0, y = 0.0; // x軸正方向の単位ベクトル
double angle_deg = 90.0; // 90度回転
double rx, ry;
rotate_vec2(x, y, angle_deg, &rx, &ry);
printf("original: (%f, %f)\n", x, y);
printf("rotated : (%f, %f)\n", rx, ry);
return 0;
}original: (1.000000, 0.000000)
rotated : (0.000000, 1.000000)このように回転処理には必ずsinとcosが登場します。
ゲームのキャラクター向き、2D物理の剛体回転、グラフの回転表示など、多くの場面で応用できます。
三角関数の誤差と実装上の注意点
三角関数は数学的にはきれいな関数ですが、コンピュータ上での実装では浮動小数点誤差が避けられません。
この章では、精度や誤差に関する実務的な注意点をまとめます。
浮動小数点誤差とsin cos計算の限界
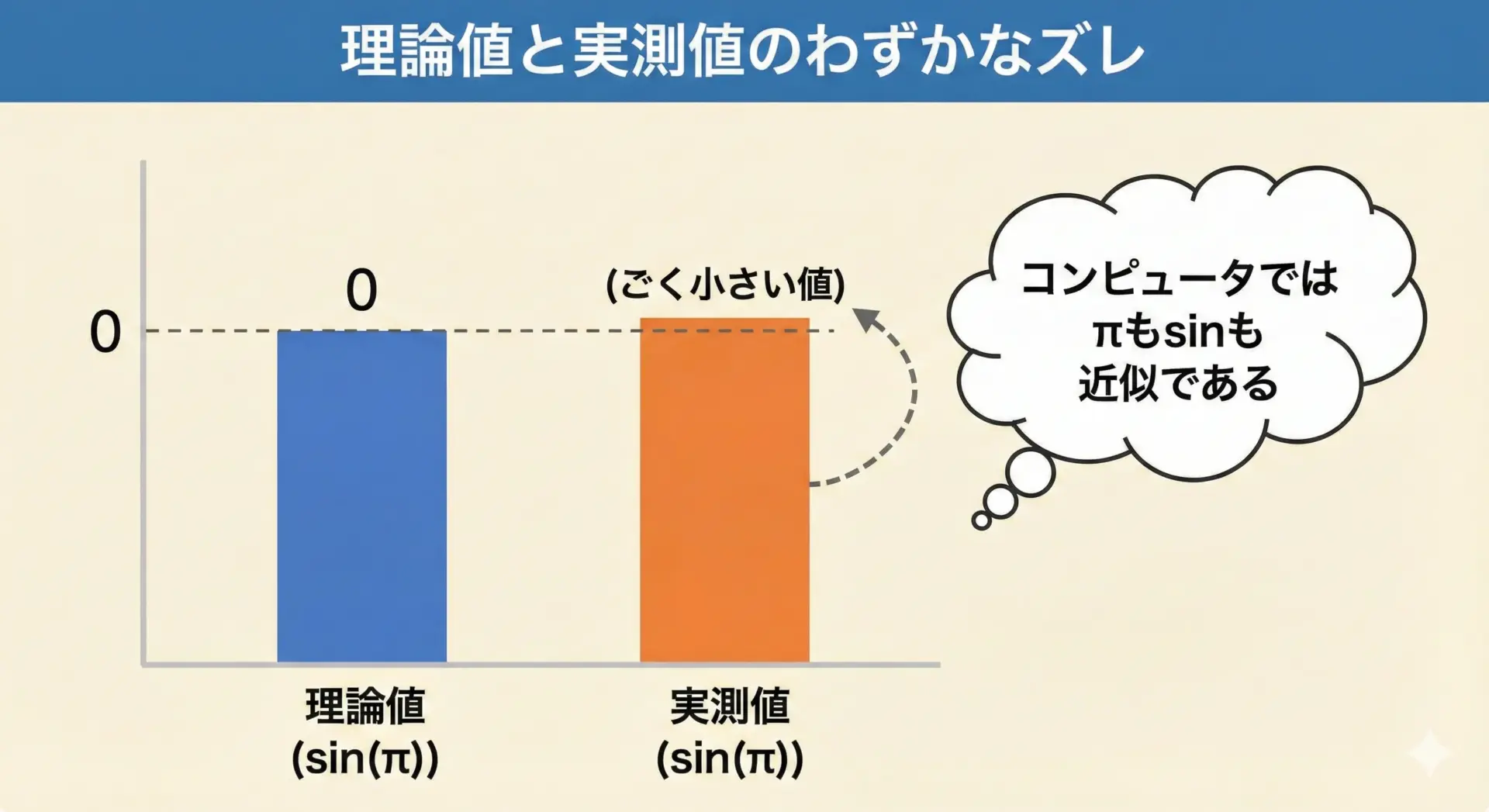
理論的にはsin(π) = 0ですが、実際にC言語で計算すると、必ずしも完全な0にはなりません。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
int main(void) {
double x = MY_PI;
double s = sin(x);
printf("sin(PI) = %.20f\n", s);
return 0;
}sin(PI) = 0.00000000000000012246ごく小さい値ですが、完全な0ではありません。
これは、π自体が有限桁で近似されていること、sin関数の内部計算も有限精度であることなど、複数の要因によるものです。
このため、浮動小数点同士を==で比較してはいけない、という有名な注意点があります。
代わりに「十分に小さいか」を見るようにします。
#include <stdio.h>
#include <math.h>
#include <float.h> // DBL_EPSILONなど
#define MY_PI 3.14159265358979323846
int main(void) {
double x = MY_PI;
double s = sin(x);
if (fabs(s) < 1e-12) { // 許容誤差の範囲内かどうかをチェック
printf("sin(PI) is effectively zero.\n");
} else {
printf("sin(PI) is not zero. value = %.20f\n", s);
}
return 0;
}角度の正規化
長時間のシミュレーションやループ計算を行うと、角度がどんどん増えて非常に大きな値になることがあります。
巨大な角度をそのままsin/cosに渡すと、精度が悪化する可能性があります。
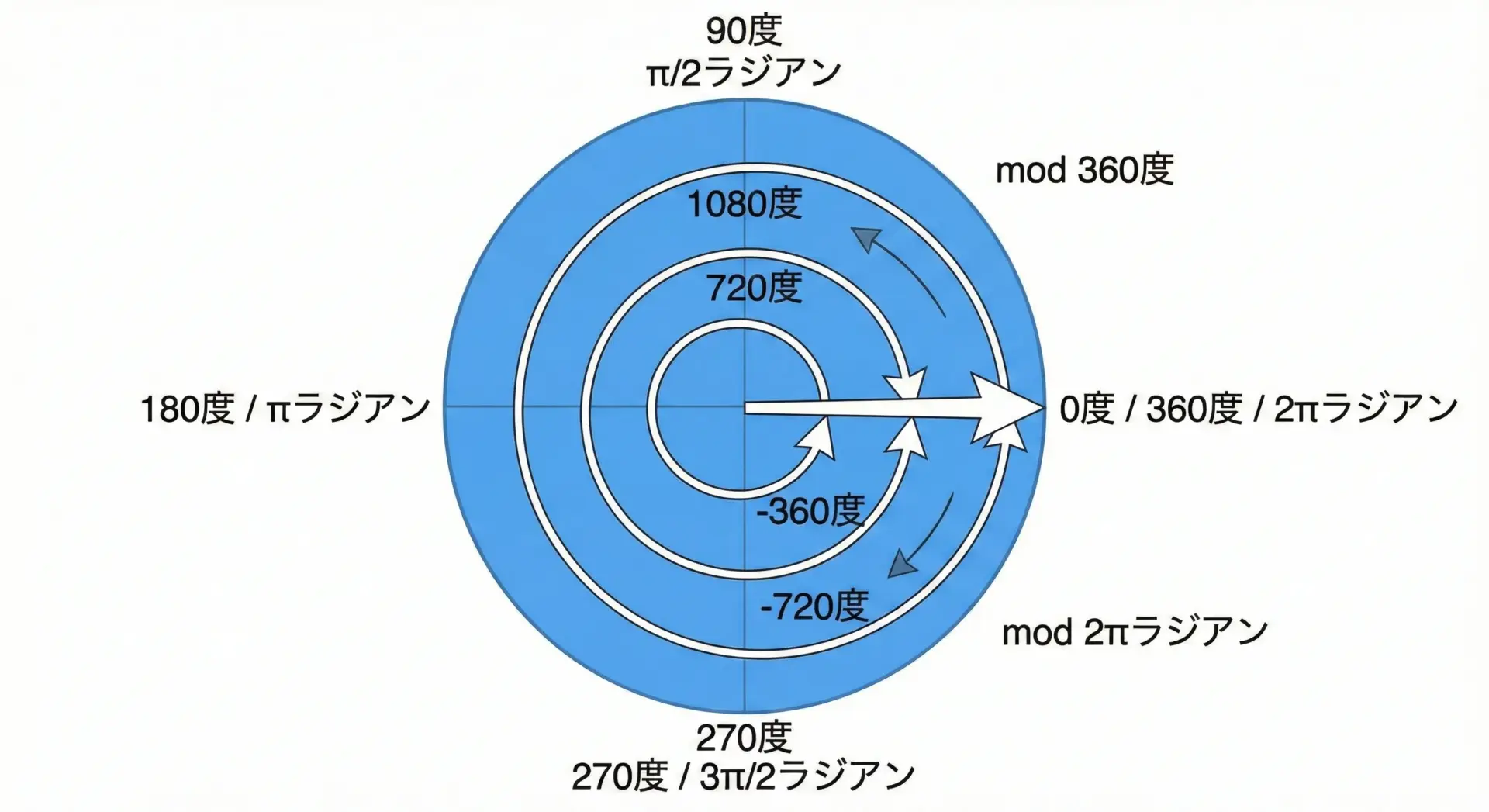
そのため、角度を一定範囲に収める「正規化」を行うのが一般的です。
度数法なら0〜360度、ラジアンなら0〜2π、あるいは-π〜+πなどがよく使われます。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
/* 角度(ラジアン)を -PI 〜 +PI の範囲に正規化する */
double normalize_angle_rad(double rad) {
// まず 0 〜 2PI の範囲に収める
double two_pi = 2.0 * MY_PI;
rad = fmod(rad, two_pi); // 余りを求める (負にもなりうる)
if (rad < -MY_PI) {
rad += two_pi;
} else if (rad > MY_PI) {
rad -= two_pi;
}
return rad;
}
int main(void) {
double angles[] = {
0.0,
5.0 * MY_PI, // 5π
-4.0 * MY_PI / 3.0 // -4π/3
};
int n = sizeof(angles) / sizeof(angles[0]);
for (int i = 0; i < n; ++i) {
double a = angles[i];
double an = normalize_angle_rad(a);
printf("original = %8.4f, normalized = %8.4f\n", a, an);
}
return 0;
}original = 0.0000, normalized = 0.0000
original = 15.7079, normalized = -0.0000
original = -4.1888, normalized = 2.0944このように正規化することで、大きすぎる角度を扱うことによる誤差やバグを抑えられます。
高速化・近似計算
sin/cosは便利ですが、計算コストは決して安くありません。
リアルタイム性が重要な処理(マイコンでの制御、ゲームの大量オブジェクト処理など)では、近似計算やテーブル参照による高速化を検討することもあります。
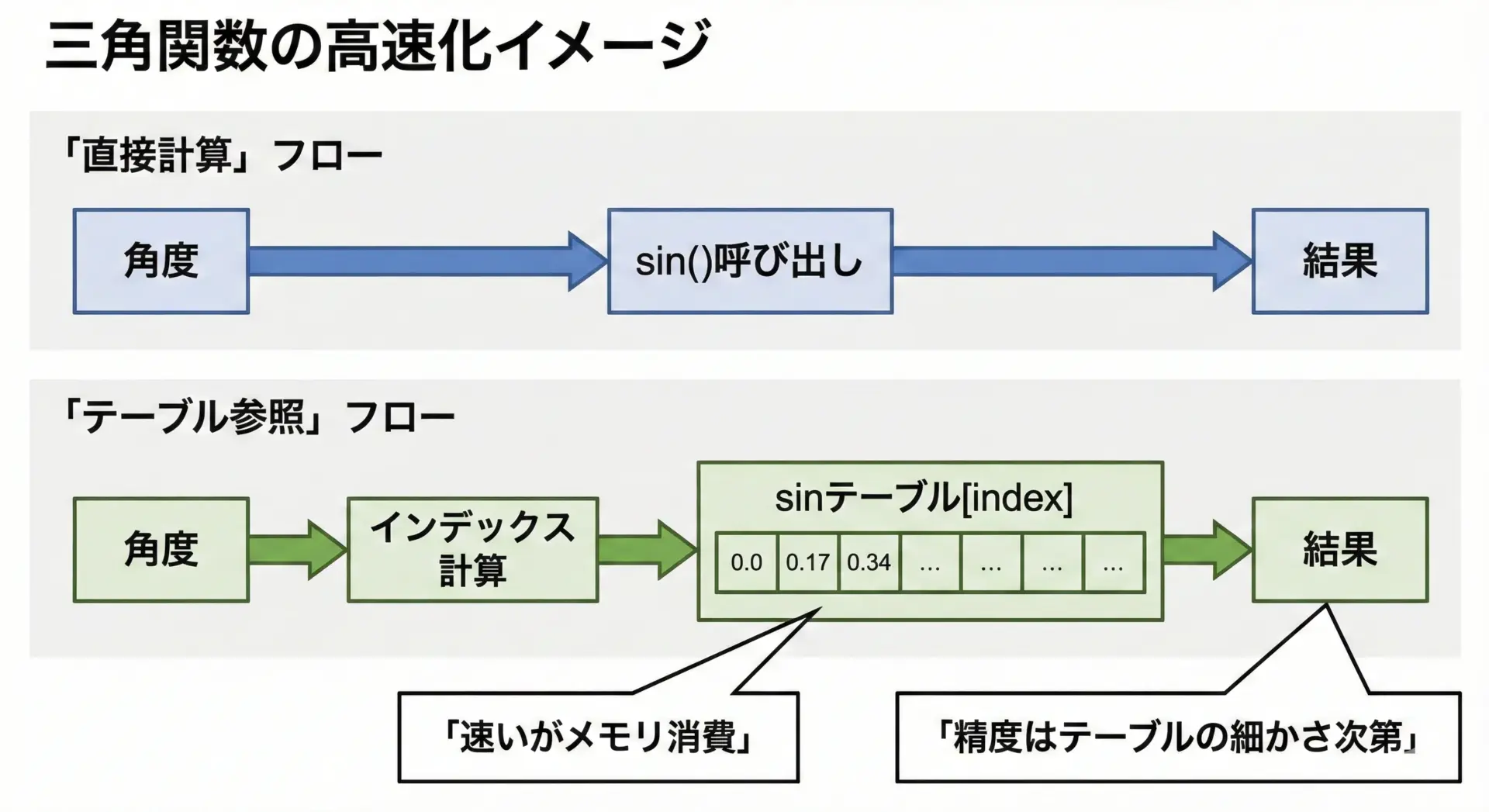
ルックアップテーブル(LUT)の例
角度の範囲や必要な精度が限定されている場合、あらかじめsin値を配列に格納しておき、配列参照で疑似的にsinを得る方法があります。
#include <stdio.h>
#include <math.h>
#define MY_PI 3.14159265358979323846
#define TABLE_SIZE 360 // 1度刻みのテーブル
double sin_table[TABLE_SIZE];
/* sinテーブルを初期化(度数法1度刻み) */
void init_sin_table(void) {
for (int deg = 0; deg < TABLE_SIZE; ++deg) {
double rad = deg * (MY_PI / 180.0);
sin_table[deg] = sin(rad); // 初期化時だけ本物のsinを使う
}
}
/* 度数法で与えられた角度から、テーブルを使って近似sin値を返す */
double fast_sin_deg(double deg) {
// 0〜359の範囲に丸める
int idx = (int)deg % TABLE_SIZE;
if (idx < 0) {
idx += TABLE_SIZE;
}
return sin_table[idx];
}
int main(void) {
init_sin_table();
for (int deg = 0; deg <= 90; deg += 15) {
double exact = sin(deg * (MY_PI / 180.0));
double approx = fast_sin_deg(deg);
printf("%3d deg: exact=% .8f, approx=% .8f, diff=% .8f\n",
deg, exact, approx, approx - exact);
}
return 0;
} 0 deg: exact= 0.00000000, approx= 0.00000000, diff= 0.00000000
15 deg: exact= 0.25881905, approx= 0.25881905, diff= 0.00000000
30 deg: exact= 0.50000000, approx= 0.50000000, diff= 0.00000000
45 deg: exact= 0.70710678, approx= 0.70710678, diff= 0.00000000
60 deg: exact= 0.86602540, approx= 0.86602540, diff= 0.00000000
75 deg: exact= 0.96592583, approx= 0.96592583, diff= 0.00000000
90 deg: exact= 1.00000000, approx= 1.00000000, diff= 0.00000000ここでは1度刻みなので、度単位ではほぼ同じ値になりますが、小数度単位の精度は失われます。
用途に応じてテーブルの細かさを決める必要があります。
他にも、テイラー展開などの多項式近似を使う方法もありますが、実装や誤差解析がやや難しくなります。
通常のアプリケーションでは、まずは標準のsin/cos/tanを素直に使うのがおすすめです。
まとめ
C言語で三角関数sin/cos/tanを扱うには、math.hのインクルードとラジアン単位の理解が欠かせません。
本記事では、度数法との変換方法、M_PIや自作PI定数の使い方、sin/cosを利用した波形生成やベクトルの回転、atan2による座標からの角度計算など、実用的なテクニックをコード付きで解説しました。
最後に、浮動小数点誤差や角度の正規化、高速化の方向性にも触れましたので、これらを踏まえて自分の用途に合った実装を選んでください。
三角関数を自在に扱えるようになれば、グラフィックスや数値計算の幅が一気に広がります。

