Pythonで整数や小数を扱うとき、なんとなくintやfloatを使っていると、思わぬ誤差やバグに悩まされます。
この記事では、「なぜ誤差が出るのか」「どう避ければよいか」を、図解とサンプルコードで丁寧に整理します。
金額計算などで失敗しないために、float誤差・round・Decimalの正しい使い方を一気に身につけましょう。
Pythonで数値型を正しく選ぶポイント
int・float・Decimalの違いと使い分け
まずはPythonでよく使う3つの数値型の性質を整理します。
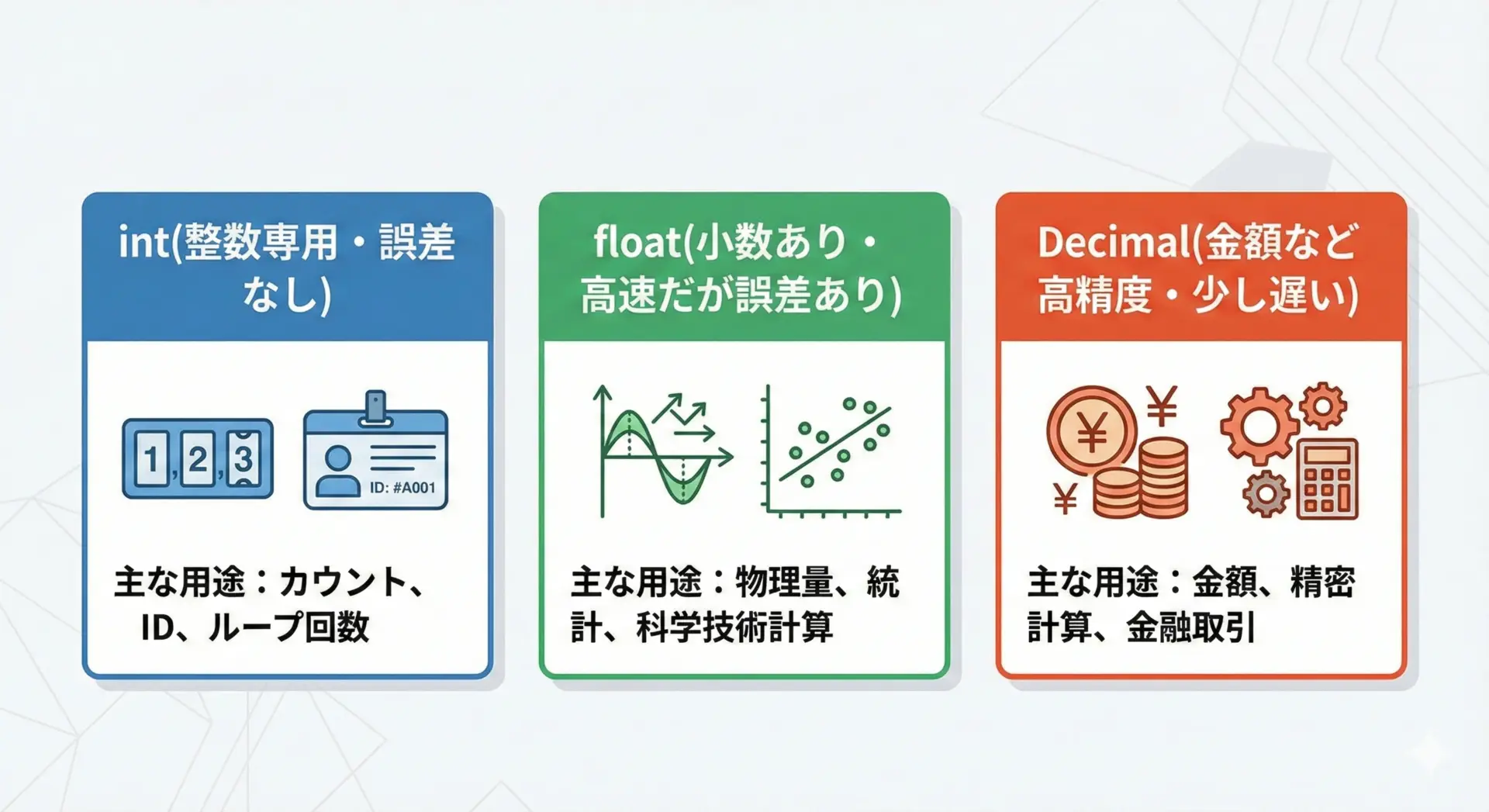
Pythonで数値を扱うときは、最初に「どの型を使うか」を決めることがとても重要です。
それぞれの特徴を表にまとめます。
| 型 | 例 | 主な用途 | 特徴 |
|---|---|---|---|
| int | 1, 0, -5, 10_000 | 個数、回数、ID、インデックス | 整数のみ・誤差なし、任意精度(桁数制限ほぼなし) |
| float | 0.1, 3.14, -2.5 | 測定値、統計、機械学習、物理量 | 高速だが誤差あり、2進数の近似表現 |
| Decimal | Decimal(“0.1”)など | 金額、税計算、為替、精密演算 | 10進数ベースで高精度、速度はfloatより遅い |
ざっくりした使い分けの指針
文章で整理すると、次のように考えると迷いにくくなります。
- カウント・ID・インデックスのように、もともと小数が入り得ないものは
intを使うべきです。ここでfloatを使う理由はほとんどありません。 - 物理量や計測値、画像処理、機械学習など、多少の誤差があっても統計的に意味がある用途では
floatを使うのが普通です。速度とメモリ効率を優先します。 - 金額や税率、誤差が1円でも困る計算では
Decimalの利用を検討すべきです。特に請求書・給与計算・決済システムなどです。
このように、「誤差がどこまで許されるか」で型を選ぶことが、バグを防ぐ第一歩です。
なぜPythonのfloatに誤差が出るのか
Pythonのfloatは、概ねC言語のdoubleに相当し、2進数で小数を表現する「浮動小数点数」です。
ここに誤差の原因があります。
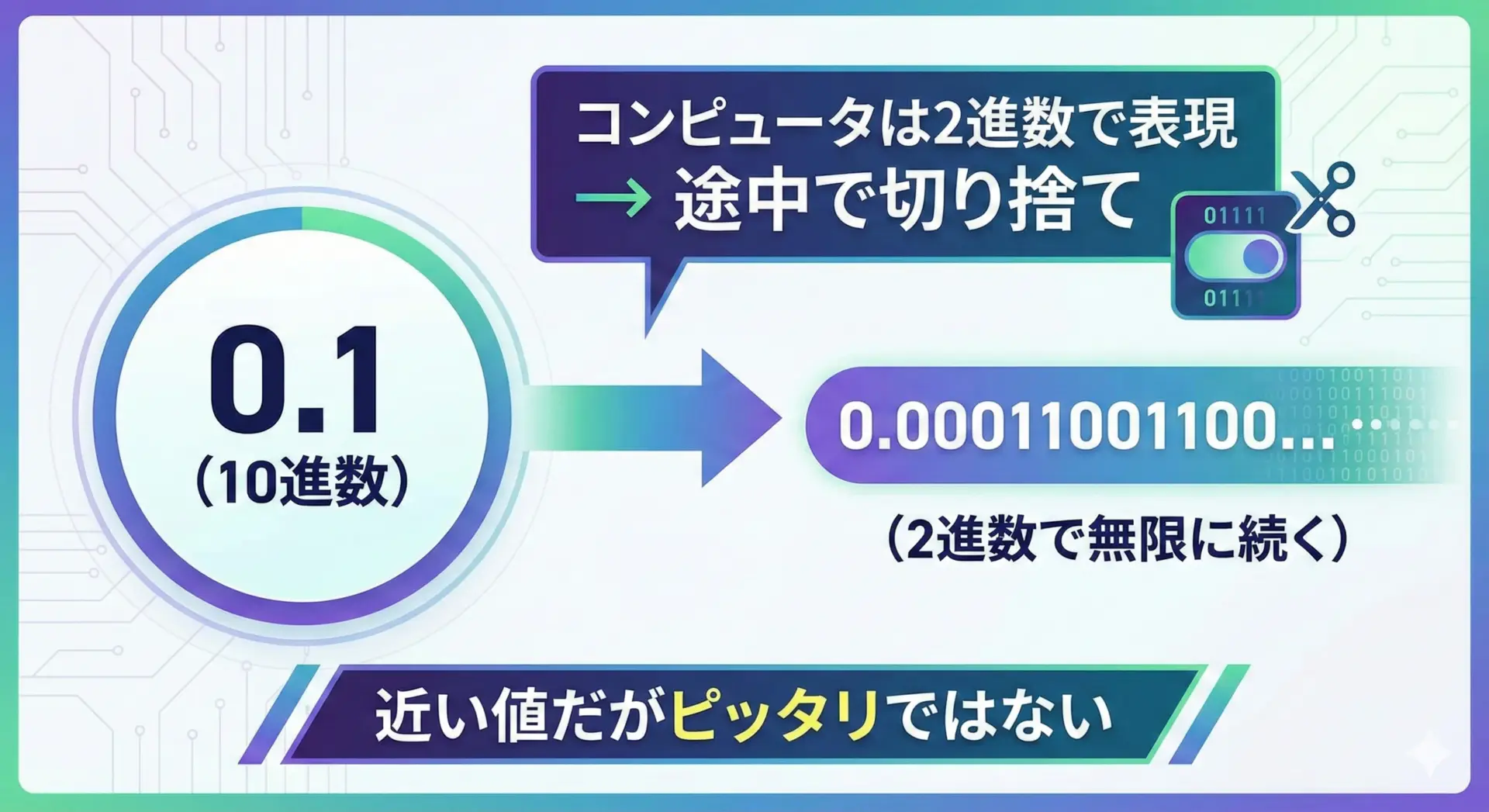
10進数では0.1はピッタリ表現できますが、2進数では0.1は無限に続く小数になります。
そのため、コンピュータ内部ではどこかで打ち切らざるを得ず、ごくわずかな誤差を含んだ「近似値」になります。
この誤差はとても小さいため、人間が通常の出力で見ると0.1に見えますが、計算を繰り返すと蓄積して目に見えるズレとなることがあります。
金額や精度が重要な場面での注意点

金額計算のように、「少数第2位まで」「1円単位で厳密に合うこと」が要求される場面でfloatをそのまま使うと、次のようなリスクがあります。
- 1件ごとの計算では小数点以下の誤差が見えないが、大量件数の合計で1円以上のズレになる。
- 合計金額と明細合計が一致せず、監査や顧客からのクレームにつながる。
- システム間で金額を照合したときに、端数処理の違いで差異が出る。
このため、金額や点数など「有限桁でピッタリ表現したい数字」はDecimalで扱うことが重要です。
floatはあくまで、誤差を許容できる数値処理用と考えると安全です。
Pythonのfloat誤差を正しく理解する
2進数表現によるfloat誤差の仕組み
float誤差は、実はPython特有の問題ではありません。
ほとんどすべての一般的なプログラミング言語で起きる「浮動小数点数の宿命」です。
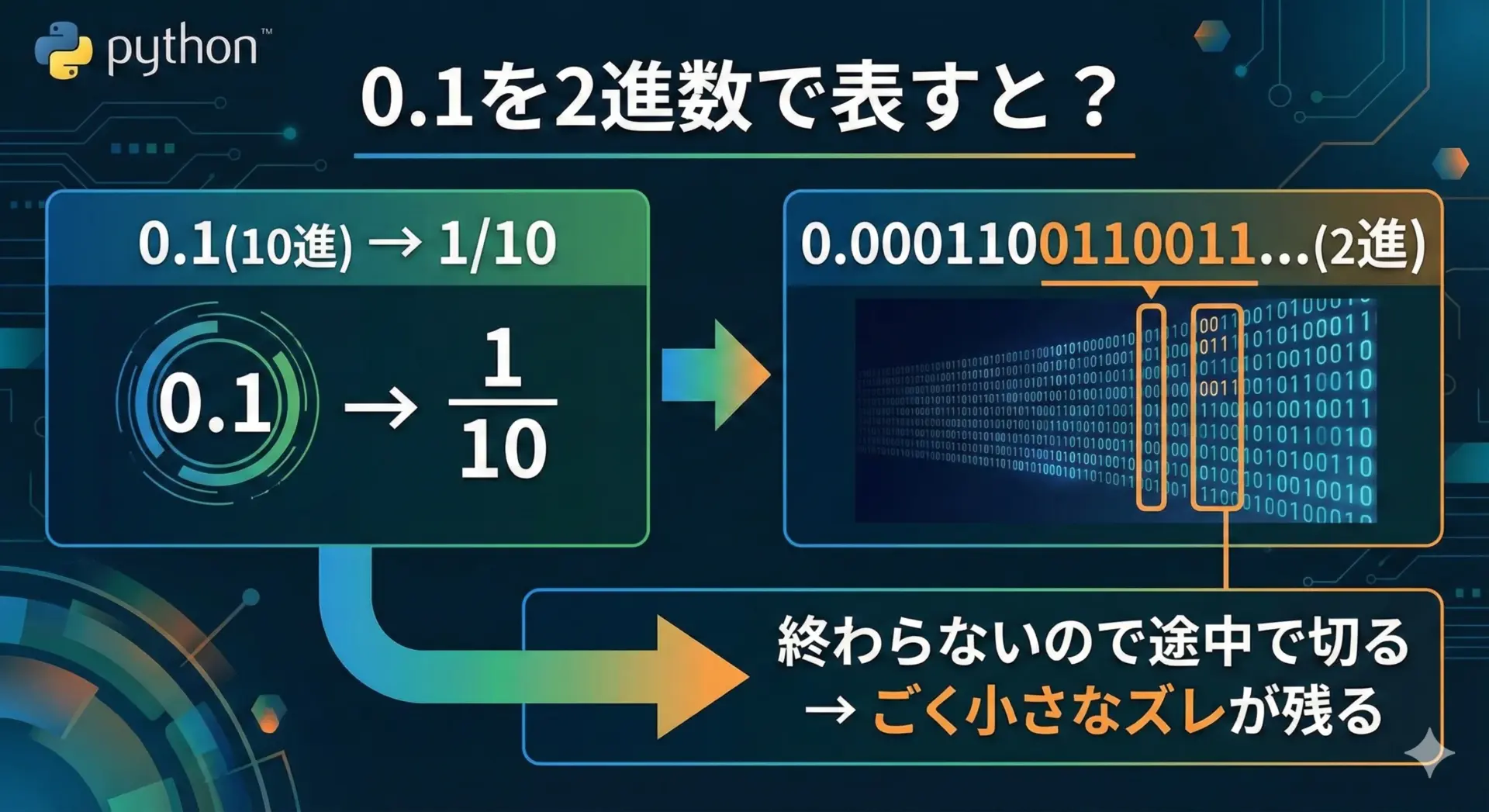
例として、0.1を2進数で表すとどうなるかを見てみます。
実際のビット列は難しいので、イメージだけ説明します。
- 10進数の
1/10(=0.1)は、2進数では0.0001100110011...と「0011」が繰り返される無限小数になります。 - しかし、コンピュータのメモリには有限のビット(例えば64ビット)しかないため、どこかで切り捨てる必要があります。
- その結果、「0.1に限りなく近いがピッタリではない値」が内部で使われます。
この「ピッタリではない」という点が、後続の計算でジワジワと効いてきます。
よくあるfloat誤差の例と落とし穴
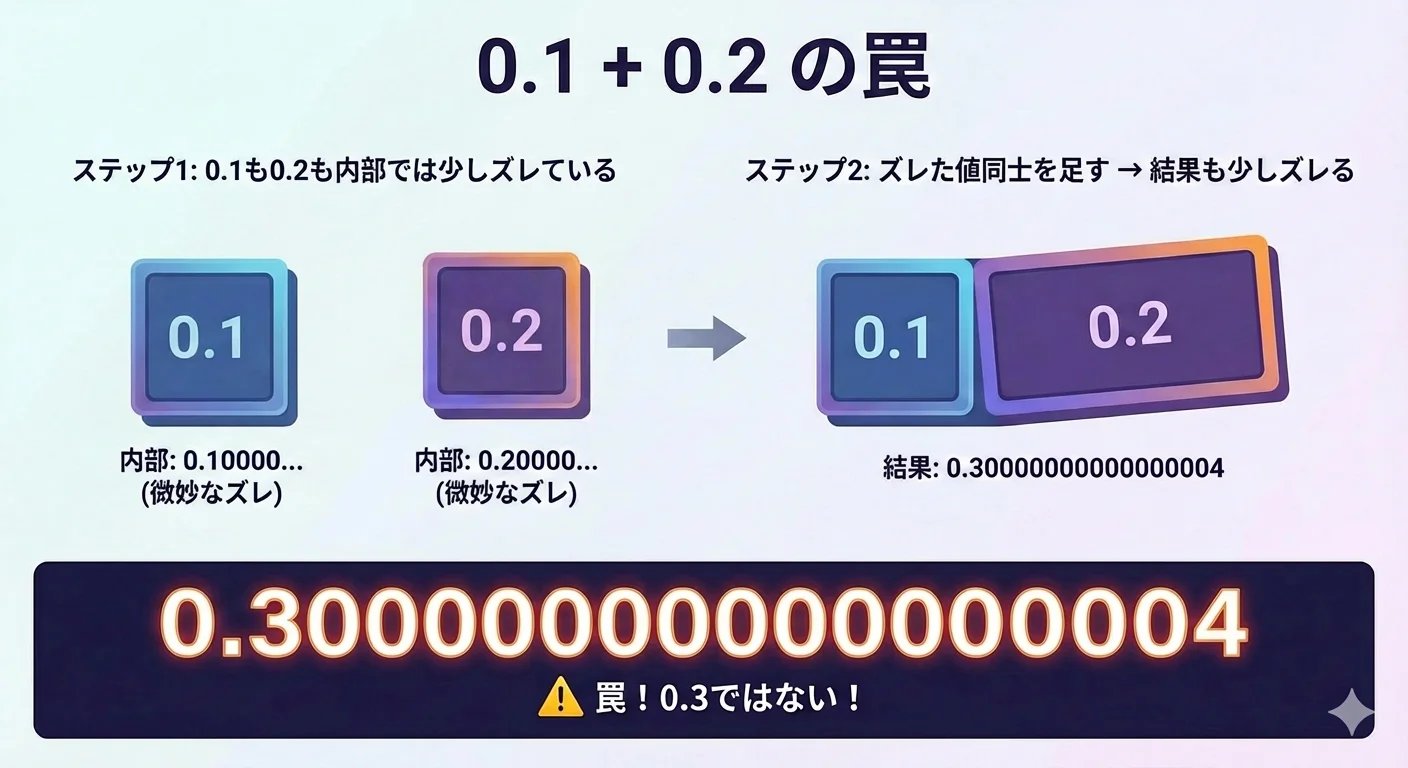
代表的な例をPythonで実際に確認してみます。
# floatの誤差を確認するサンプル
a = 0.1
b = 0.2
c = a + b
print("a =", a)
print("b =", b)
print("a + b =", c)
# 期待は 0.3 だが...
print("a + b == 0.3 ?", c == 0.3)a = 0.1
b = 0.2
a + b = 0.30000000000000004
a + b == 0.3 ? False典型的な落とし穴は次のようなものです。
- 比較演算で
==を使ってしまい、Trueにならない。 - 合計値にわずかな誤差が混ざり、
0.3のはずが0.30000000000000004と表示される。 - 一度誤差が出てしまうと、繰り返し計算で誤差が蓄積しやすい。
「floatは誤差を含む近似値」という前提で設計し、誤差を前提としたコードを書くことが重要になります。
比較演算(==)と誤差許容比較(isclose)の使い方
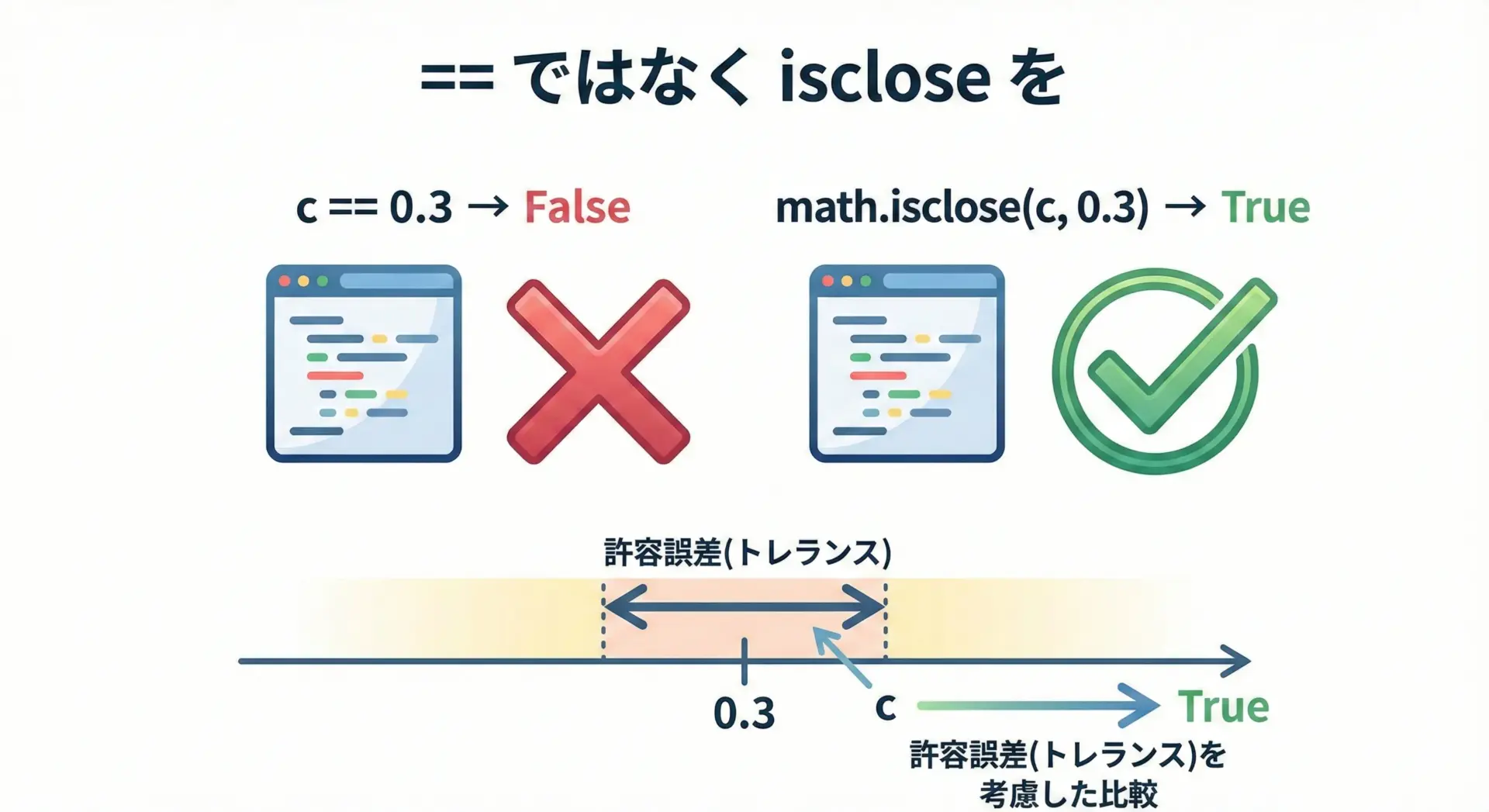
float同士を比較するときに==を使うのは危険です。
Python 3.5以降では、math.iscloseを使って「十分近ければ同じとみなす」比較ができます。
import math
x = 0.1 + 0.2
y = 0.3
print("x =", x)
print("y =", y)
# 危険な比較
print("x == y :", x == y)
# 安全な比較 (許容誤差つき)
print("math.isclose(x, y) :", math.isclose(x, y))
# 許容誤差(相対誤差, 絶対誤差)を自分で指定する例
print("厳しめの比較 :", math.isclose(x, y, rel_tol=1e-12, abs_tol=0.0))x = 0.30000000000000004
y = 0.3
x == y : False
math.isclose(x, y) : True
厳しめの比較 : True数値計算でfloatを使うなら、「float比較はisclose」くらいの気持ちでいると安全です。
特にテストコードではassert x == yではなく、math.iscloseで比較する習慣をつけるとよいです。
round関数と小数処理の基本
Pythonのroundの仕様と注意点
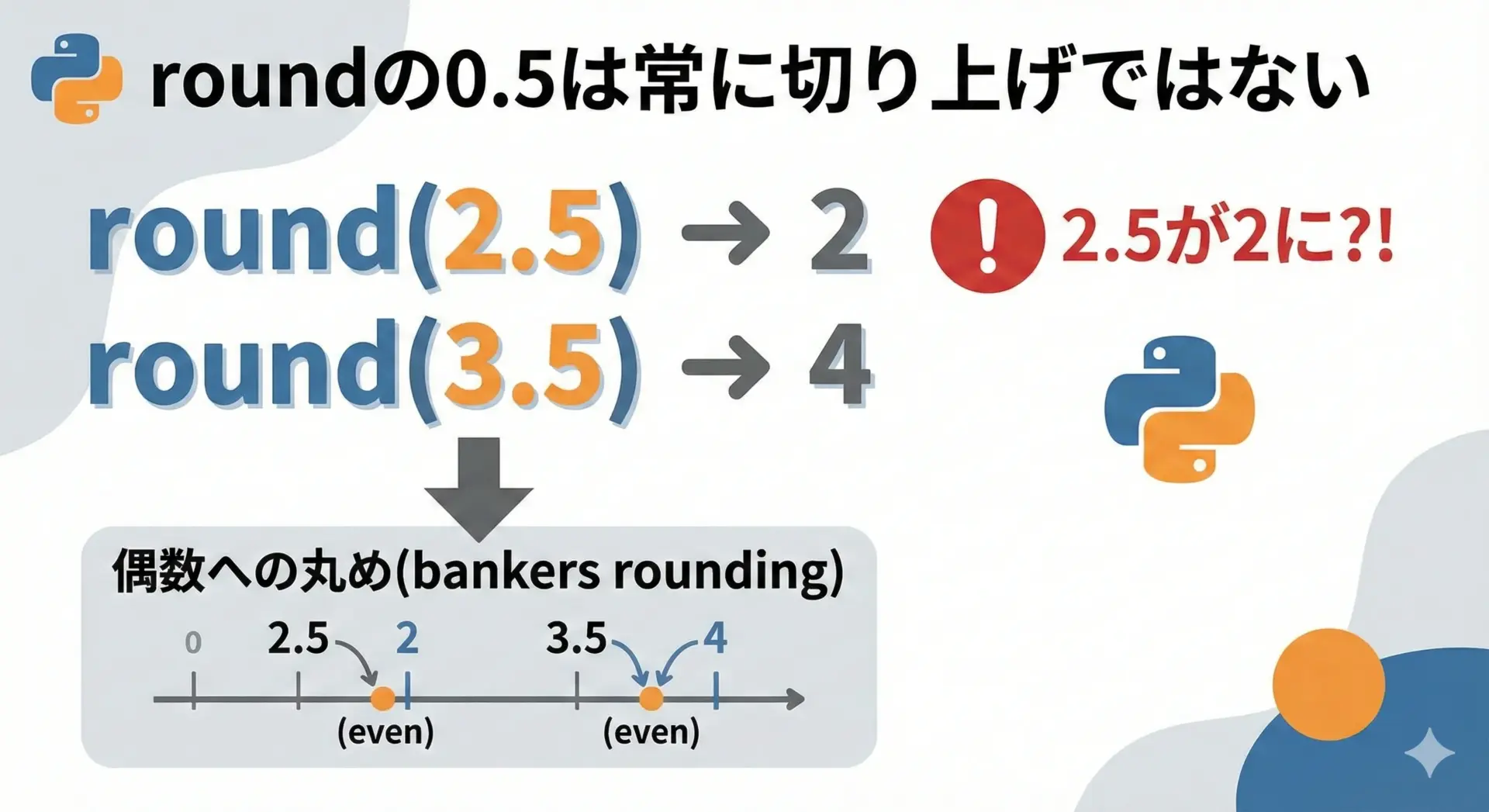
Pythonのroundは、「0.5は常に切り上げる」わけではない点に注意が必要です。
Pythonのroundは「偶数への丸め(銀行丸め, banker’s rounding)」を採用しています。
print(round(2.5)) # 期待通り? 3ではない
print(round(3.5))
print(round(1.5))
print(round(2.5))
print(round(4.5))2
4
2
2
4これは、0.5ちょうどの場合、一番近い偶数へ丸めるというルールです。
統計的にバイアスを減らすために採用されていますが、「常に0.5を切り上げ」と思い込んでいるとバグの原因になります。
桁数を指定した四捨五入・切り上げ・切り捨て
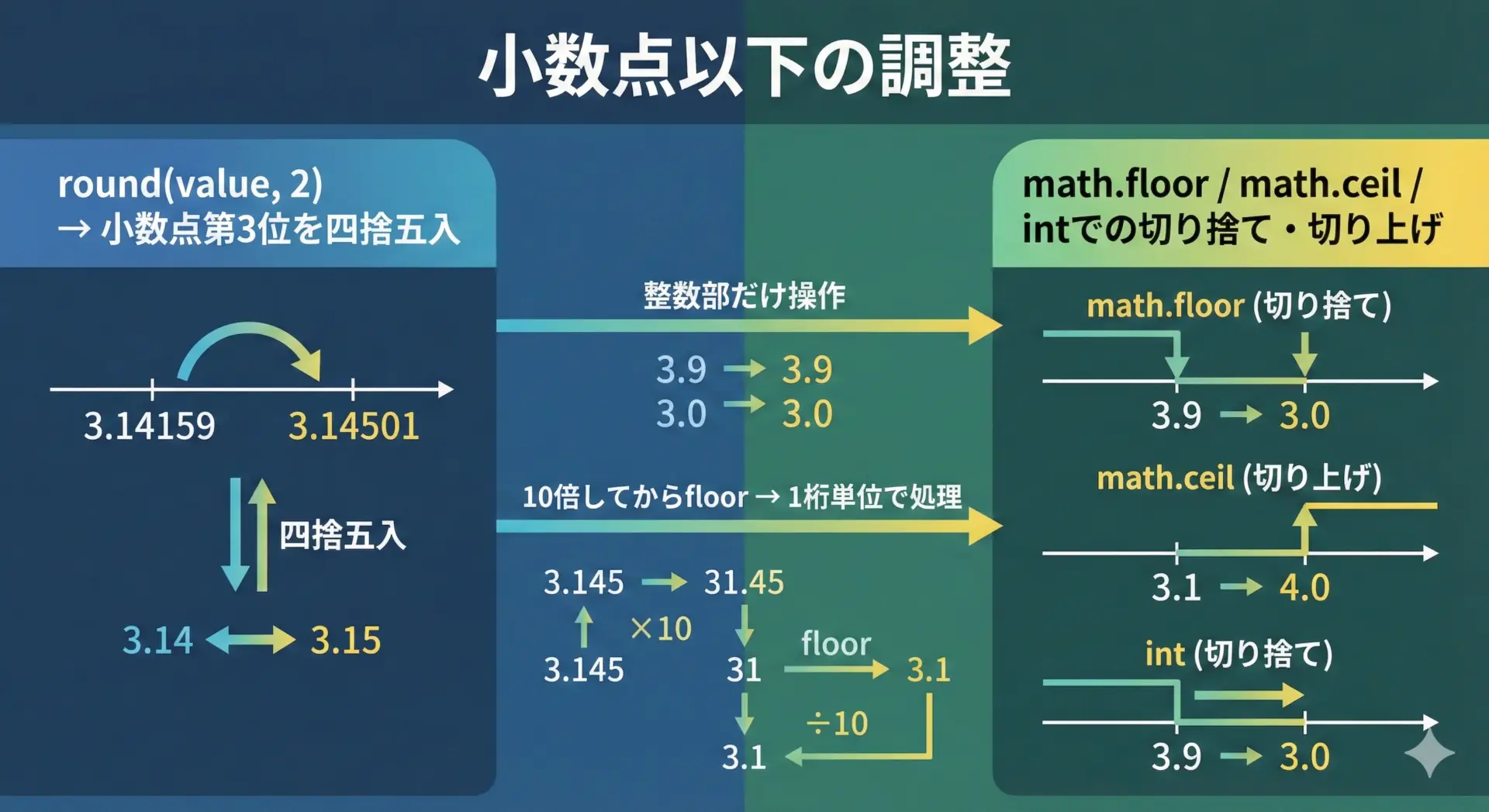
roundには第2引数で桁数を指定できます。
value = 123.4567
print(round(value, 0)) # 小数第1位で四捨五入 → 整数に
print(round(value, 1)) # 小数第2位で四捨五入
print(round(value, 2)) # 小数第3位で四捨五入
print(round(value, -1)) # 10の位で四捨五入
print(round(value, -2)) # 100の位で四捨五入123.0
123.5
123.46
120.0
100.0一方で、「切り上げ」「切り捨て」をしたい場合はmathモジュールを使うのが定石です。
import math
x = 12.345
# 切り捨て
print("floor(x) =", math.floor(x)) # 12
# 切り上げ
print("ceil(x) =", math.ceil(x)) # 13
# 0方向へ切り捨て (正ならfloor, 負ならceilと同じ方向)
print("truncate(x) =", math.trunc(x)) # 12
# 小数第2位で切り捨てをしたい場合は、一旦10倍してから戻す
print("小数第2位で切り捨て =", math.floor(x * 100) / 100)floor(x) = 12
ceil(x) = 13
truncate(x) = 12
小数第2位で切り捨て = 12.34ただし、ここでもfloat誤差の影響を受けるため、金額のような厳密さが必要な場面ではDecimalを使った方が安全です。
金融計算でroundだけに頼ってはいけない理由
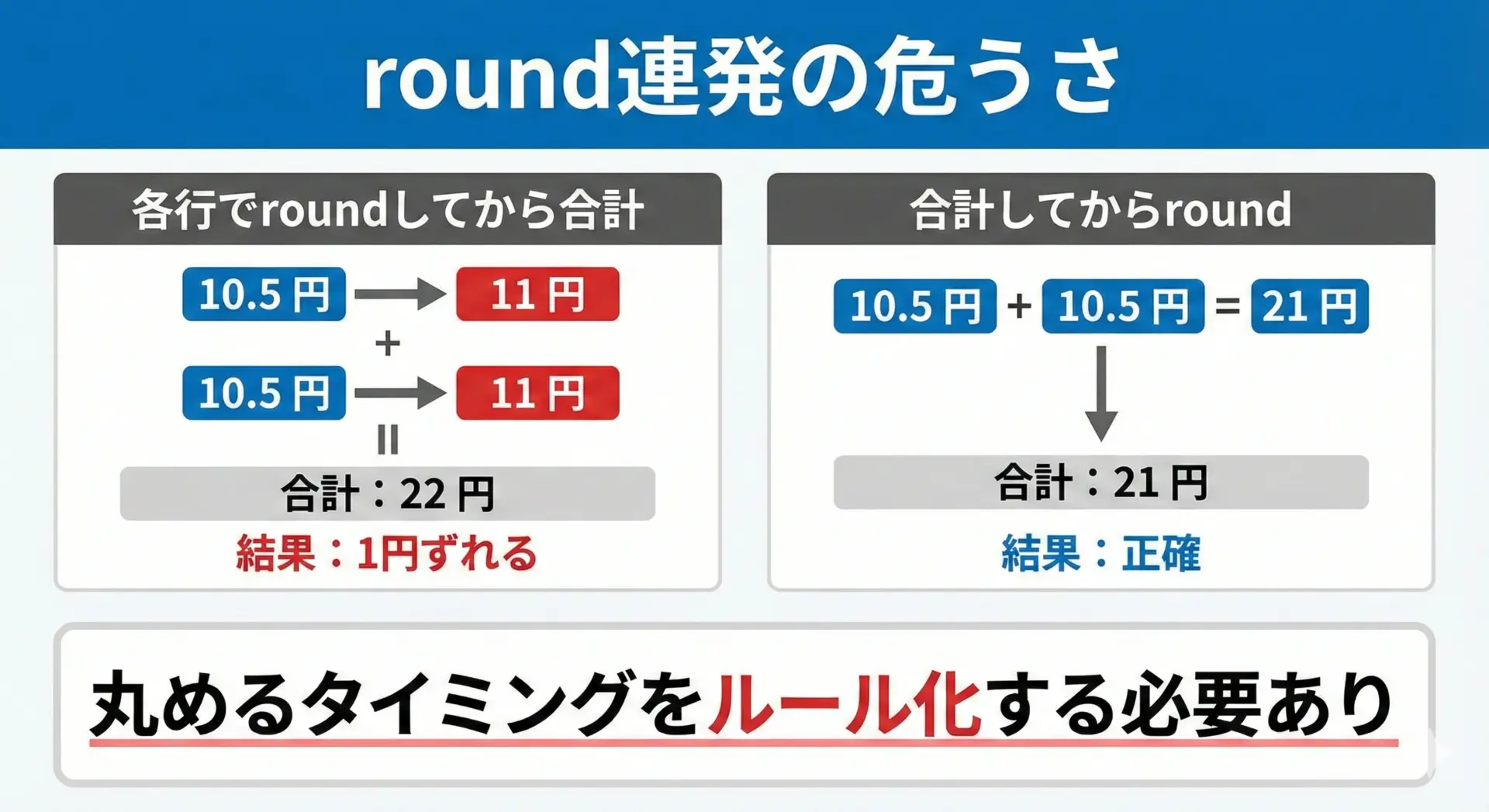
金融計算では、「どのタイミングで丸めるか」が結果に大きく影響します。
たとえば、次のようなケースを考えます。
# 商品ごとに税込価格を計算する例
prices = [100.0, 200.0, 300.0] # 税抜価格
tax_rate = 0.1 # 消費税10%
# パターンA: 各行をroundしてから合計
total_a = 0
for p in prices:
price_with_tax = p * (1 + tax_rate)
total_a += round(price_with_tax) # 各行を四捨五入(整数円に)
# パターンB: 合計を出してから最後にround
subtotal = sum(prices)
total_b = round(subtotal * (1 + tax_rate))
print("パターンA(行ごとに丸め) :", total_a)
print("パターンB(まとめて丸め) :", total_b)パターンA(行ごとに丸め) : 660
パターンB(まとめて丸め) : 660この例ではたまたま同じになりますが、端数が出る価格の組み合わせでは1円以上の差が生まれることがあります。
重要なのは次の点です。
- ビジネスルールとして「行ごと丸め」なのか「合計で丸め」なのかを決めておく。
- 「roundしておけば安全」ではない。丸めの仕様をドキュメント化し、システム全体で統一する。
- 浮動小数点の誤差に加えて、丸めタイミングの違いでも結果がブレるため、Decimalと一貫した丸めルールの組み合わせが必要になる。
Decimalで整数・小数を正確に計算する
Decimalの基本
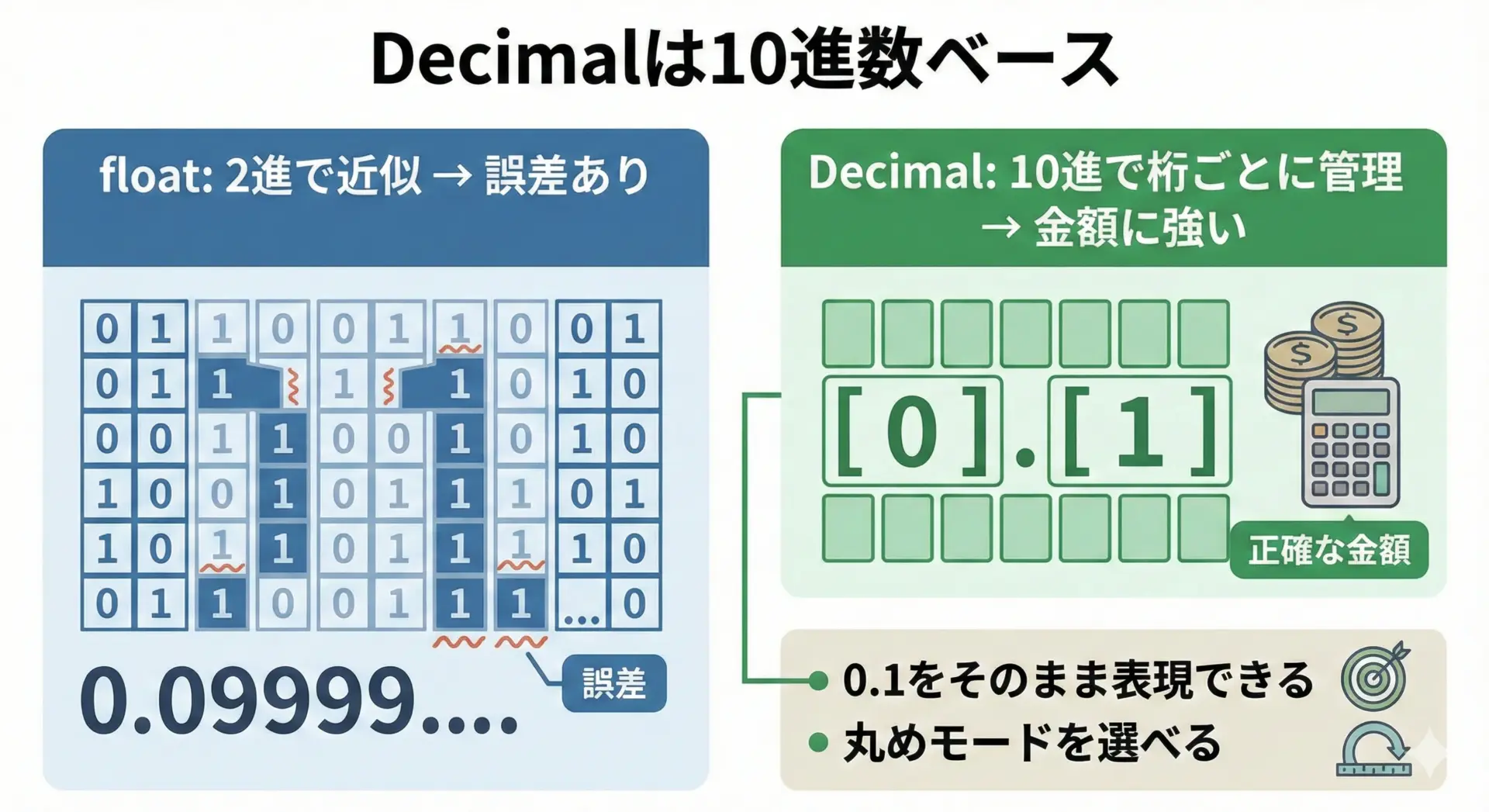
decimal.Decimalは、10進数の世界で高精度な計算をするためのクラスです。
金額や税率など、誤差が許されない場面で活躍します。
基本的な使い方は次のようになります。
from decimal import Decimal
# Decimalの基本
a = Decimal("0.1") # 文字列から生成するのが重要(理由は後述)
b = Decimal("0.2")
c = a + b
print("a =", a)
print("b =", b)
print("a + b =", c)
print("a + b == Decimal('0.3') ?", c == Decimal("0.3"))a = 0.1
b = 0.2
a + b = 0.3
a + b == Decimal('0.3') ? True0.1 + 0.2 がピッタリ 0.3 になることが確認できます。
これはDecimalが10進数の桁をそのまま扱うためです。
floatからではなく文字列からDecimalを作る理由
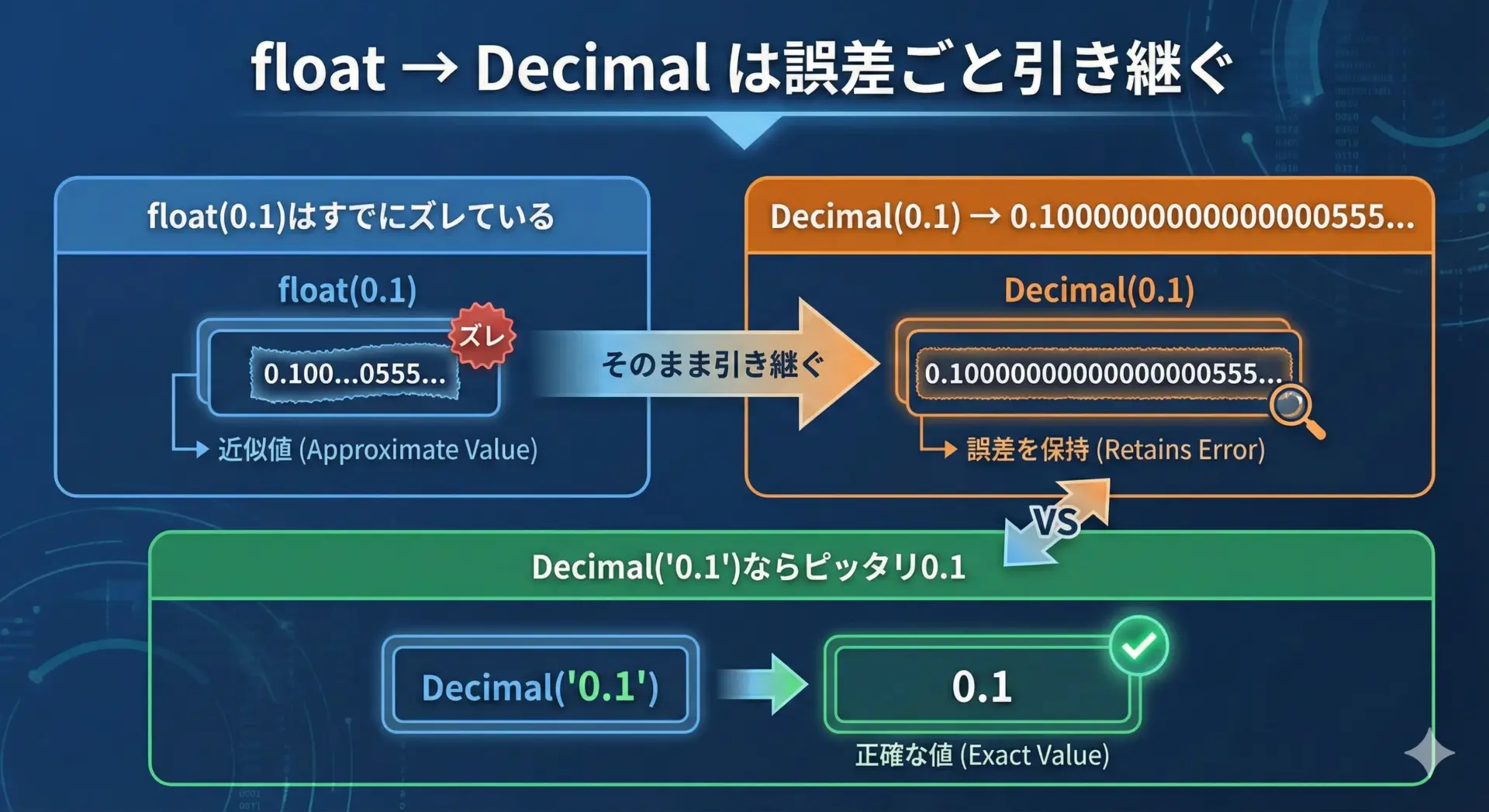
Decimalを使うときにもっとも大事なポイントが、floatから直接Decimalを作らないことです。
from decimal import Decimal
# 悪い例: floatからDecimalを作る
x_float = 0.1
x_dec_from_float = Decimal(x_float)
# 良い例: 文字列からDecimalを作る
x_dec_from_str = Decimal("0.1")
print("floatの0.1 :", x_float)
print("Decimal(0.1) :", x_dec_from_float)
print("Decimal('0.1') :", x_dec_from_str)
print("どちらが等しいか? :", x_dec_from_float == x_dec_from_str)floatの0.1 : 0.1
Decimal(0.1) : 0.1000000000000000055511151231
Decimal('0.1') : 0.1
どちらが等しいか? : Falseこの例からわかるように、floatの誤差をDecimalに「持ち込んで」しまうと、せっかくの高精度が台無しになります。
そのため、外部から受け取る入力(文字列)の段階でDecimalに変換することが重要です。
WebフォームやCSVなどの文字列データで受け取り、すぐにDecimal("...")にしてしまうのが安全なパターンです。
Decimalで金額計算を正確に行う実践パターン
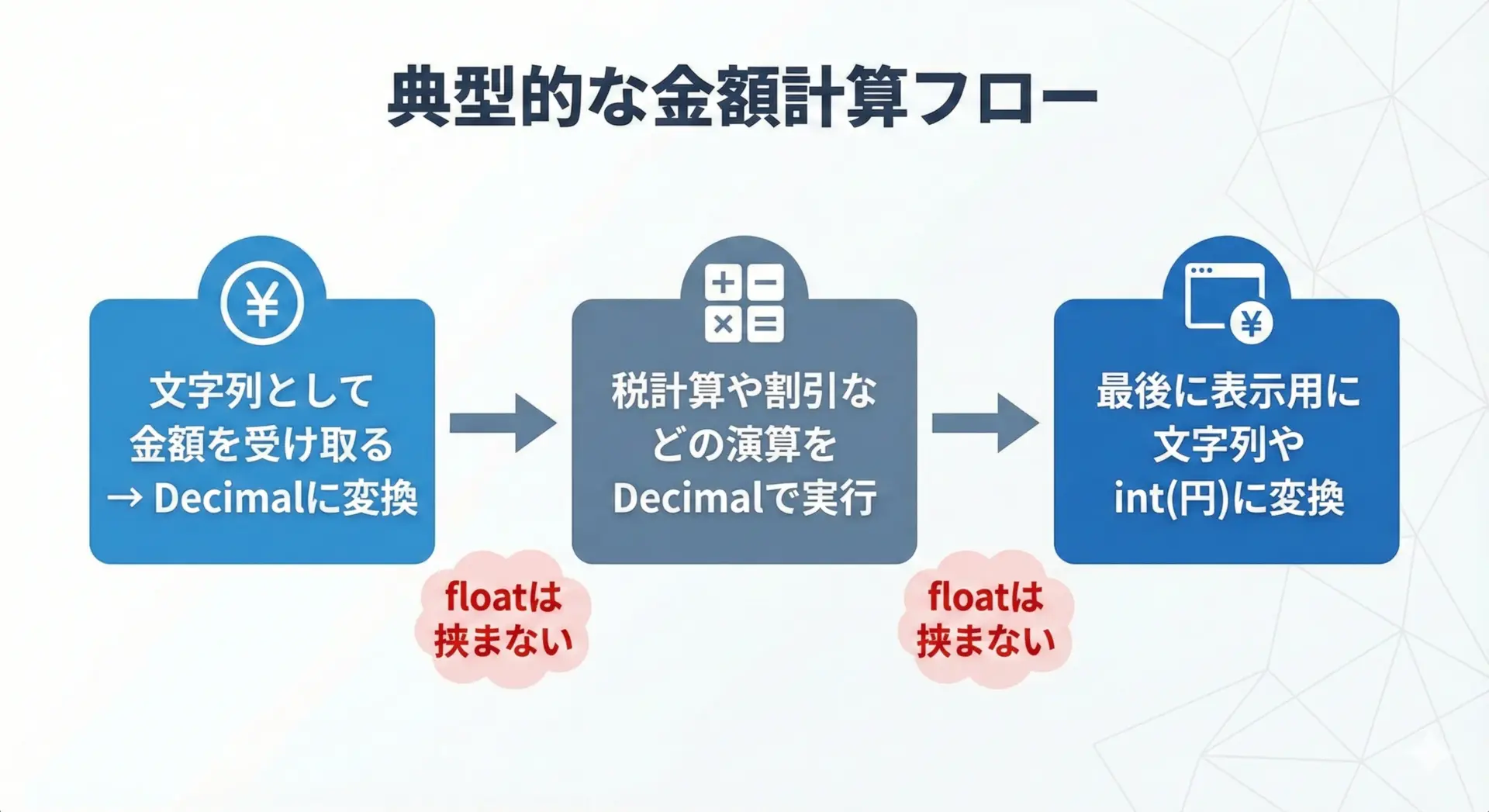
典型的な税込金額計算を、Decimalで書いてみます。
from decimal import Decimal, ROUND_HALF_UP, getcontext
# コンテキスト(精度や丸めモード)の設定
# 必要に応じて精度を高める(ここでは28桁のまま)
getcontext().prec = 28
# 入力は文字列から受け取る想定
price_str = "1980" # 税抜価格(円)
tax_rate_str = "0.10" # 消費税率 10%
# 文字列からDecimalを作る
price = Decimal(price_str)
tax_rate = Decimal(tax_rate_str)
# 税額と税込価格を計算(ここでは小数第2位まで保持)
tax = (price * tax_rate).quantize(Decimal("0.01"), rounding=ROUND_HALF_UP)
price_with_tax = (price + tax).quantize(Decimal("0.01"), rounding=ROUND_HALF_UP)
print("税抜価格 :", price) # 1980
print("税額(円) :", tax) # 198.00
print("税込価格 :", price_with_tax) # 2178.00税抜価格 : 1980
税額(円) : 198.00
税込価格 : 2178.00ポイントは次の通りです。
- 最初から最後までDecimalだけで完結させる。
- 税率もDecimalで表現し、途中でfloatに変換しない。
.quantize(Decimal("0.01"), rounding=...)で小数第2位までに丸める。これが実務でよく使うパターンです。
Decimalとroundの組み合わせ方と丸めモード
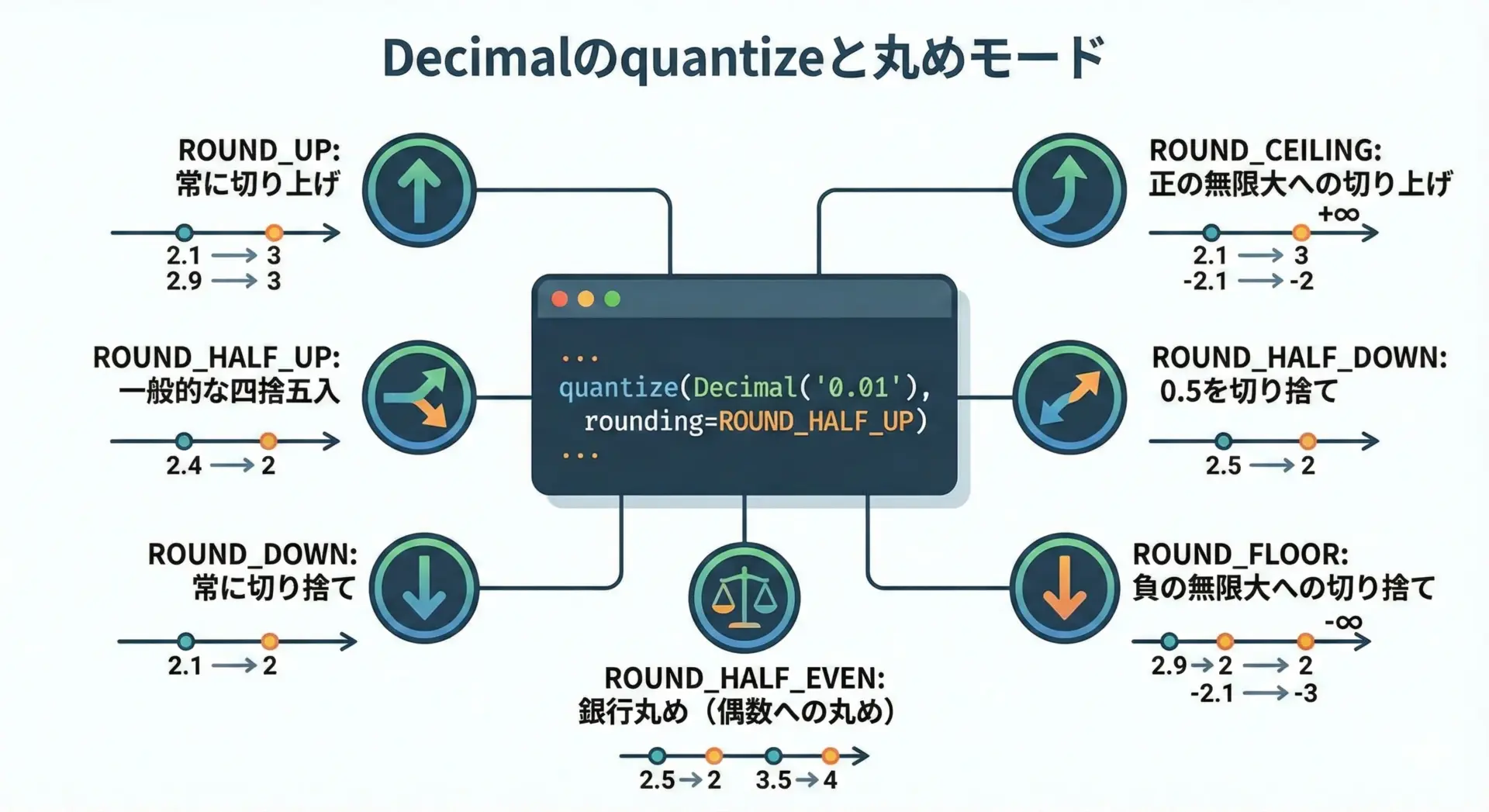
Decimalには独自の丸めメソッドquantizeがあり、丸めモードを細かく指定できます。
roundと混同しやすいですが、Decimalを使うならquantizeを使うのが基本です。
from decimal import Decimal, ROUND_HALF_UP, ROUND_DOWN, ROUND_UP
x = Decimal("123.4567")
# 小数第2位までに四捨五入(いわゆる一般的な四捨五入)
y_half_up = x.quantize(Decimal("0.01"), rounding=ROUND_HALF_UP)
# 小数第2位までに切り捨て
y_down = x.quantize(Decimal("0.01"), rounding=ROUND_DOWN)
# 小数第2位までに切り上げ
y_up = x.quantize(Decimal("0.01"), rounding=ROUND_UP)
print("元の値 :", x)
print("四捨五入(HALF_UP):", y_half_up)
print("切り捨て(DOWN) :", y_down)
print("切り上げ(UP) :", y_up)元の値 : 123.4567
四捨五入(HALF_UP): 123.46
切り捨て(DOWN) : 123.45
切り上げ(UP) : 123.46主な丸めモードには次のようなものがあります。
| 定数名 | 意味 | よくある用途 |
|---|---|---|
| ROUND_HALF_UP | 一般的な四捨五入(0.5以上切り上げ) | 日本での金額四捨五入など |
| ROUND_HALF_DOWN | 0.5は切り捨て、それより大きければ切り上げ | 特殊な業務ルール |
| ROUND_HALF_EVEN | 偶数への丸め(Pythonのroundと同じ) | 統計・会計の一部 |
| ROUND_UP | 常に0から離れる方向に丸め(絶対値増加) | 安全側に倒す計算 |
| ROUND_DOWN | 常に0に近づく方向に丸め(絶対値減少) | 顧客有利な切り捨てなど |
業務要件に応じてどの丸めモードを使うかを明示し、コード上でも定数で指定することで、「なんとなくroundした結果」が変わってしまうリスクを減らせます。
パフォーマンスと精度のトレードオフ
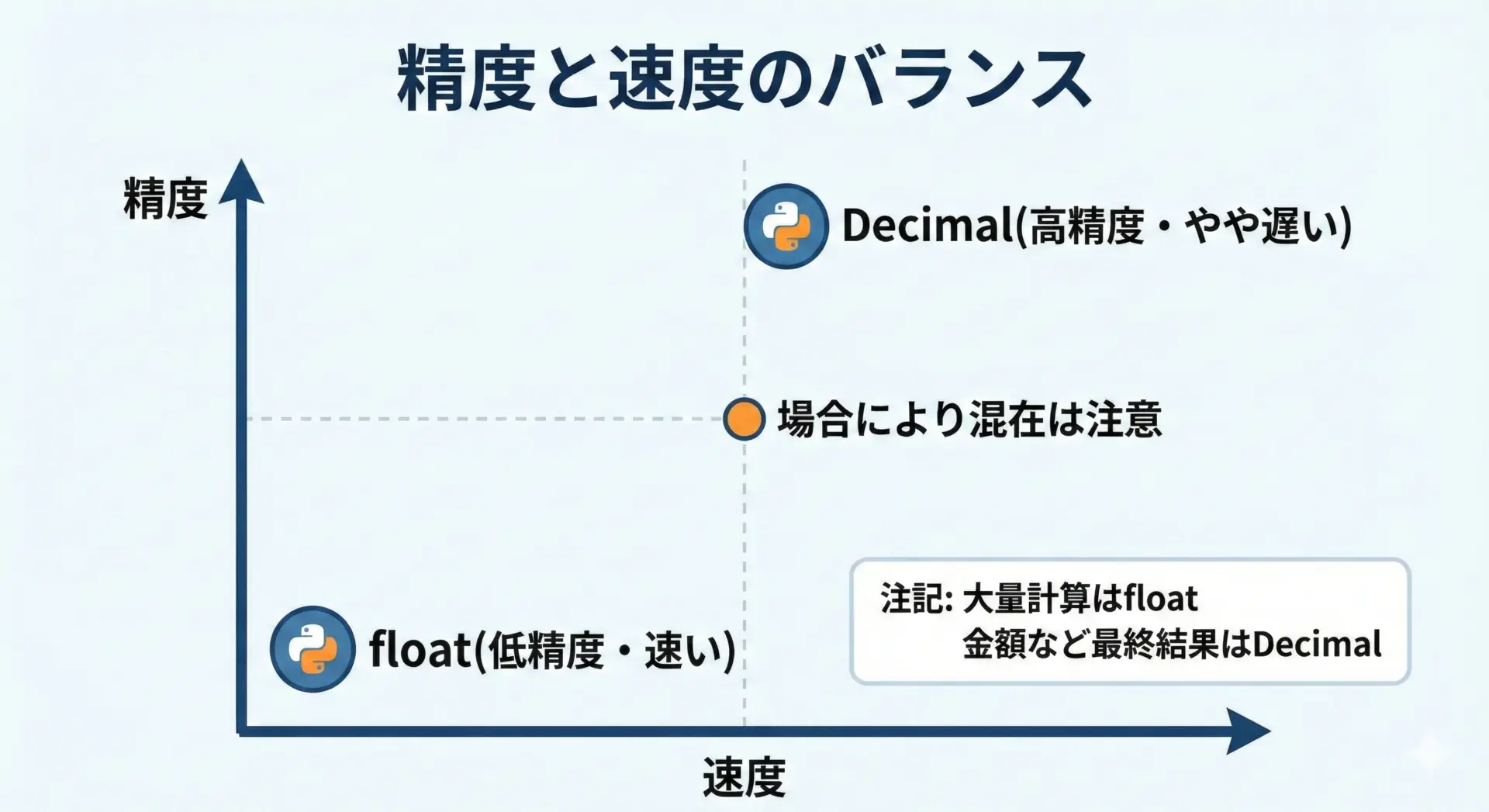
Decimalは高精度ですが、floatに比べると計算速度が遅いというデメリットがあります。
大まかな感覚として、数倍〜十数倍程度遅くなるケースもあります。
import time
from decimal import Decimal
# 試しに簡易ベンチマーク(おおよその感覚)
N = 1_00000
start = time.time()
x = 0.0
for _ in range(N):
x += 0.1
end = time.time()
print("float 結果:", x, "時間:", end - start)
start = time.time()
y = Decimal("0.0")
d = Decimal("0.1")
for _ in range(N):
y += d
end = time.time()
print("Decimal結果:", y, "時間:", end - start)※実際の時間は環境によって大きく異なります。
金融システムを設計するときには、次のような考え方が現実的です。
- ビジネス的に意味のある金額はDecimalで管理する。(請求金額、残高、税額など)
- 機械学習用の特徴量計算や統計処理など、多少の誤差があっても問題ない部分はfloatで計算する。
- 途中でfloatとDecimalを混ぜない。どうしても混在させる場合は、境界を明確にし、変換ルールを決める。
「全部Decimal」にすれば安全ですが、性能や開発コストとのバランスも考えて、どこまで厳密さが必要かを判断することが重要です。
まとめ
Pythonで整数と小数を正確に扱うには、「どの型を使うか」「誤差と丸めをどう管理するか」を意識することが欠かせません。
整数カウントにはint、誤差許容の数値計算にはfloat、金額や高精度計算にはDecimalと役割分担し、比較にはmath.isclose、Decimalではquantizeと丸めモードを使い分けます。
この記事の内容を押さえておけば、float誤差に悩まされることなく、安心してPythonで数値計算を設計できるようになります。