Pythonでプログラムを書くとき、リスト・タプル・セットのどれを使うか迷うことは少なくありません。
この記事では、3つのコレクションの特徴を整理しながら、「この場面ではこれを使う」という具体的な使い分けパターンを詳しく解説します。
図解やサンプルコードを通して、実務でそのまま使える判断基準を身につけていきましょう。
Pythonのリスト・タプル・セットの基本比較
リスト・タプル・セットの違いを一気に理解する

Pythonでよく使うコレクションのうち、リスト(list)、タプル(tuple)、セット(set)は見た目も用途も少しずつ違います。
ここではまず、この3つの「性格の違い」をざっくり押さえることから始めます。
以下の表は、リスト・タプル・セットの主要な性質をまとめたものです。
| 種類 | リテラル表記 | 順序 | 変更可否 | 重複 | 主な用途 |
|---|---|---|---|---|---|
| list | [1, 2, 3] | あり | 変更可(ミュータブル) | 許可 | 一般的な「並び」「可変の配列」 |
| tuple | (1, 2, 3) | あり | 変更不可(イミュータブル) | 許可 | 「固定された組」「レコード」 |
| set | {1, 2, 3} | なし | 変更可(ミュータブル) | 不可(一意) | 集合演算・重複排除・高速検索 |
まずは「順序」「変更可否」「重複」の3点を見れば、どれを選ぶかの大枠は決まります。
以降のセクションでは、この3軸をベースに詳しく見ていきます。
ミュータブルとイミュータブルの違い

Pythonでは、オブジェクトをその場で変更できるかどうかが非常に重要です。
- ミュータブル(変更可能): 中身をあとから書き換えたり、追加・削除できます。
- 例: list, dict, set など
- イミュータブル(変更不可): 作られたあとで中身を変えることはできません。
- 例: tuple, int, float, str など
タプルはイミュータブル、リストとセットはミュータブルです。
これが、関数の引数や戻り値、辞書のキー、マルチスレッドなどの文脈で、どれを選ぶかに大きく影響します。
簡単なコードで違いを確認してみます。
# リスト(list)はミュータブルなので書き換え可能
nums = [1, 2, 3]
nums[0] = 10 # 先頭要素を書き換え
nums.append(4) # 要素を追加
print(nums)
# タプル(tuple)はイミュータブルなので書き換え不可
t = (1, 2, 3)
# t[0] = 10 # これはエラーになる(TypeError)
print(t)[10, 2, 3, 4]
(1, 2, 3)「絶対に書き換えてほしくないデータかどうか」が、リストとタプルを選ぶうえでの重要な判断材料になります。
順序あり・なしと重複可・不可の整理

もう一つ重要なのが、「順序があるか」「重複を許すか」です。
- 順序あり:
- 要素の並び順が意味を持ちます。
- インデックス番号でアクセスできます。
- 対象: list, tuple
- 順序なし:
- 並び順に意味はありません。
- インデックスでのアクセスはできません。
- 対象: set
- 重複可:
- 同じ値を複数回入れても区別して扱われます。
- list, tuple は重複した値をそのまま保持可能です。
- 重複不可:
- 同じ値は1つだけ保持されます。
- set は自動的に重複を取り除きます。
簡単な例を示します。
# リストとタプルは順序あり・重複可
lst = [1, 2, 2, 3]
tpl = (1, 2, 2, 3)
print(lst[0]) # インデックスでアクセス可能
print(tpl[1]) # インデックスでアクセス可能
print(lst) # 重複した 2 がそのまま残る
# セットは順序なし・重複不可
s = {1, 2, 2, 3}
print(s) # 2 は1つだけになる(順序は保証されない)1
2
[1, 2, 2, 3]
{1, 2, 3}「順序が必要か」「重複を許したいか」を考えると、セットを選ぶべきか、リスト/タプルを選ぶべきかがはっきりしてきます。
リスト(list)を使うべきパターン
順序を保ちたいときのPythonリスト活用パターン
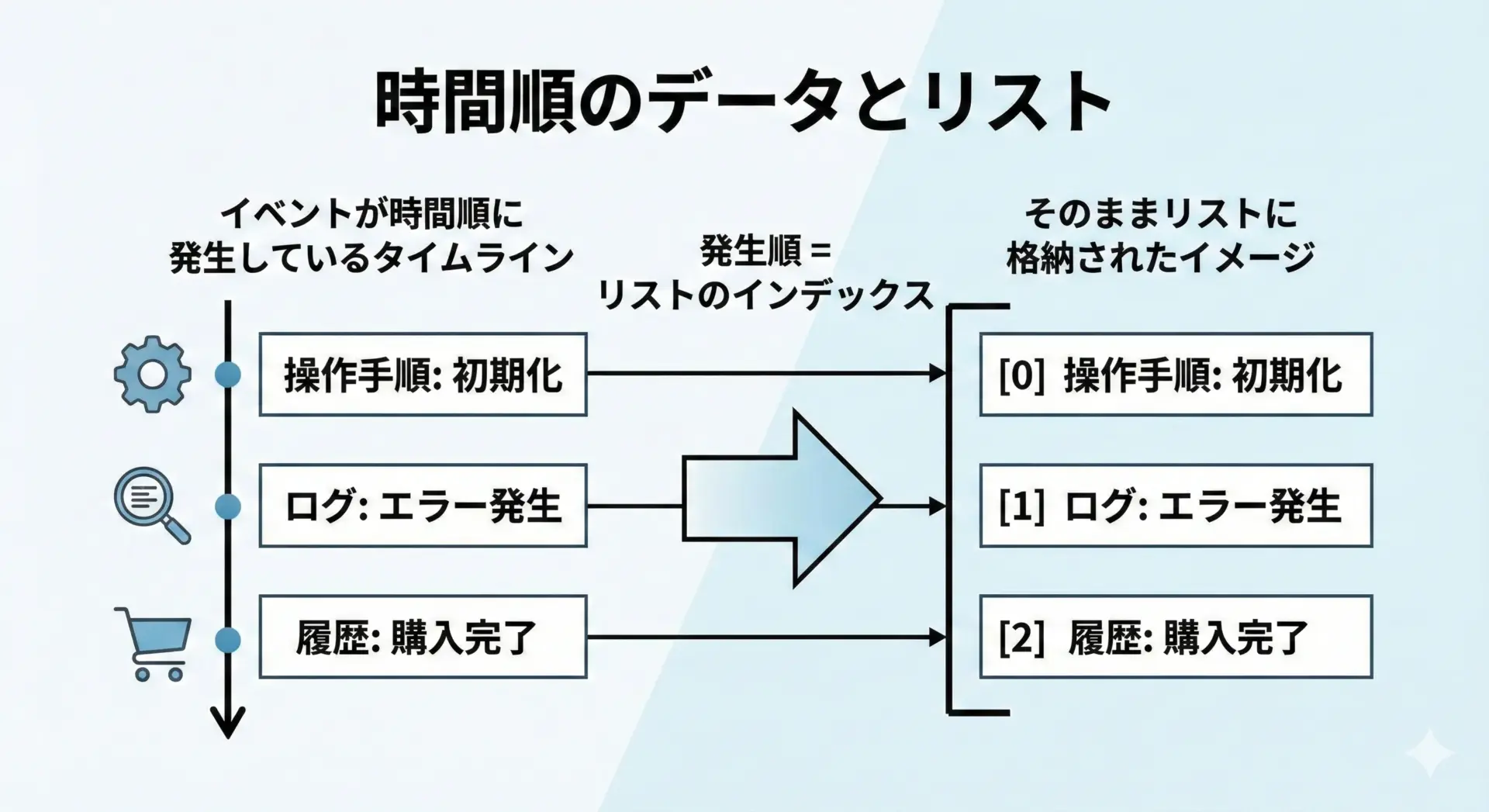
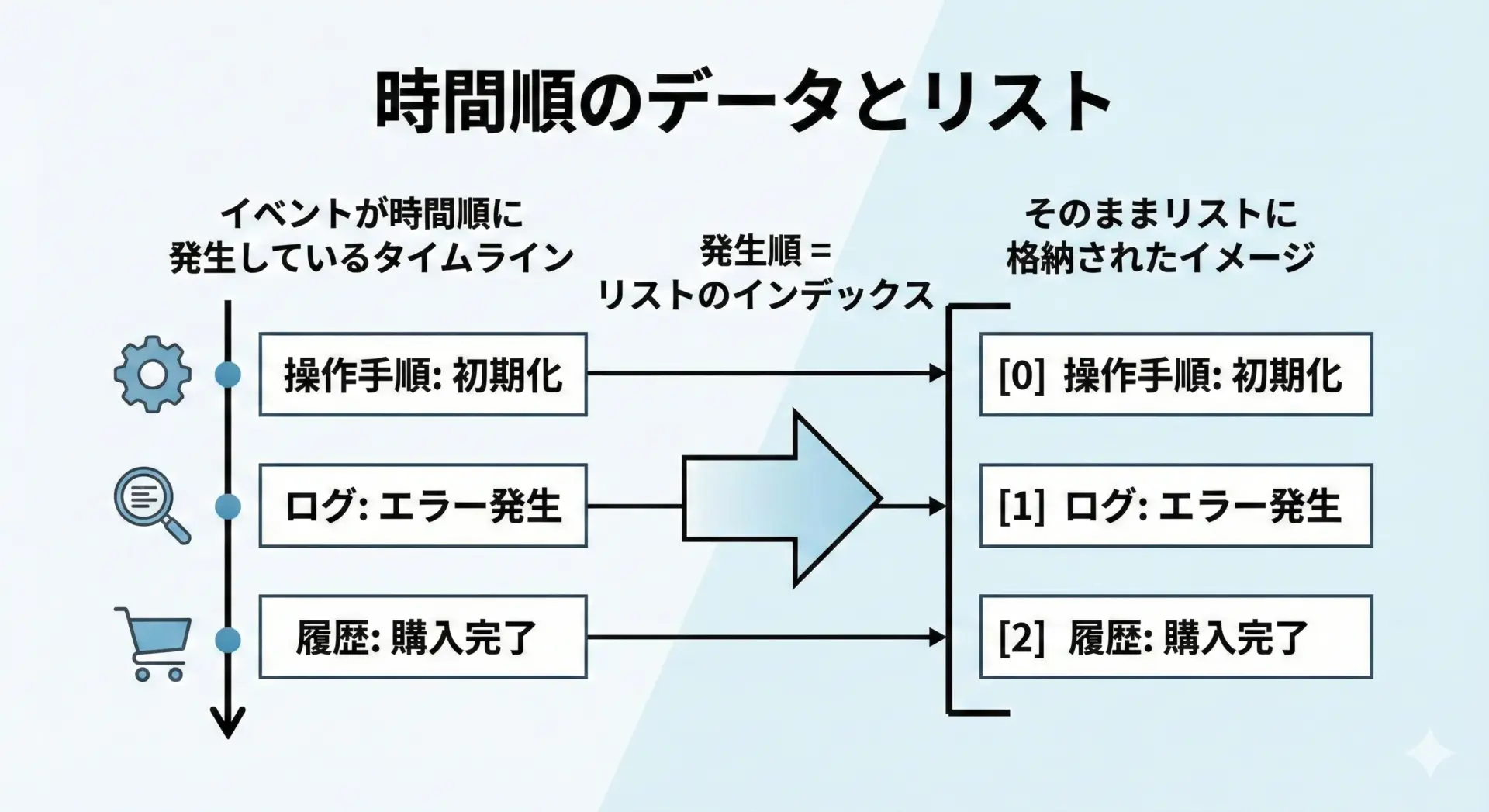
要素の並び順がそのまま意味を持つデータには、基本的にリストを使います。
たとえば、以下のようなケースです。
- 時系列のデータ(ログ、履歴、センサー値など)
- 表示順が重要なメニューやナビゲーション
- 並んでいる順番に意味がある手順やステップ
簡単な使用例です。
# 時系列の温度データ(最新順)
temperatures = [22.5, 23.0, 23.3, 24.1]
# 最初の計測値と最新の計測値を取り出す
first = temperatures[0]
latest = temperatures[-1]
print("最初:", first)
print("最新:", latest)最初: 22.5
最新: 24.1このように「順番がそのまま情報になっている」場合、リストが第一候補になります。
要素を追加・削除しながら扱う場合のリストの使いどころ
リストはミュータブルなので、あとから要素を追加したり削除したりする前提のデータ構造に向いています。
例えば、処理待ちのタスクキューや、画面上の現在のアイテム一覧など、状態が変化し続けるものです。
# 処理待ちのタスク一覧
tasks = ["download", "resize_image"]
# 新しいタスクを追加
tasks.append("upload")
print("追加後:", tasks)
# 先頭のタスクを取り出して処理(簡易的なキュー)
current = tasks.pop(0)
print("処理中:", current)
print("残り:", tasks)追加後: ['download', 'resize_image', 'upload']
処理中: download
残り: ['resize_image', 'upload']このような「増えたり減ったりする前提のコレクション」では、リストを選択するのが自然です。
同じ値をそのまま保持したいときのリスト
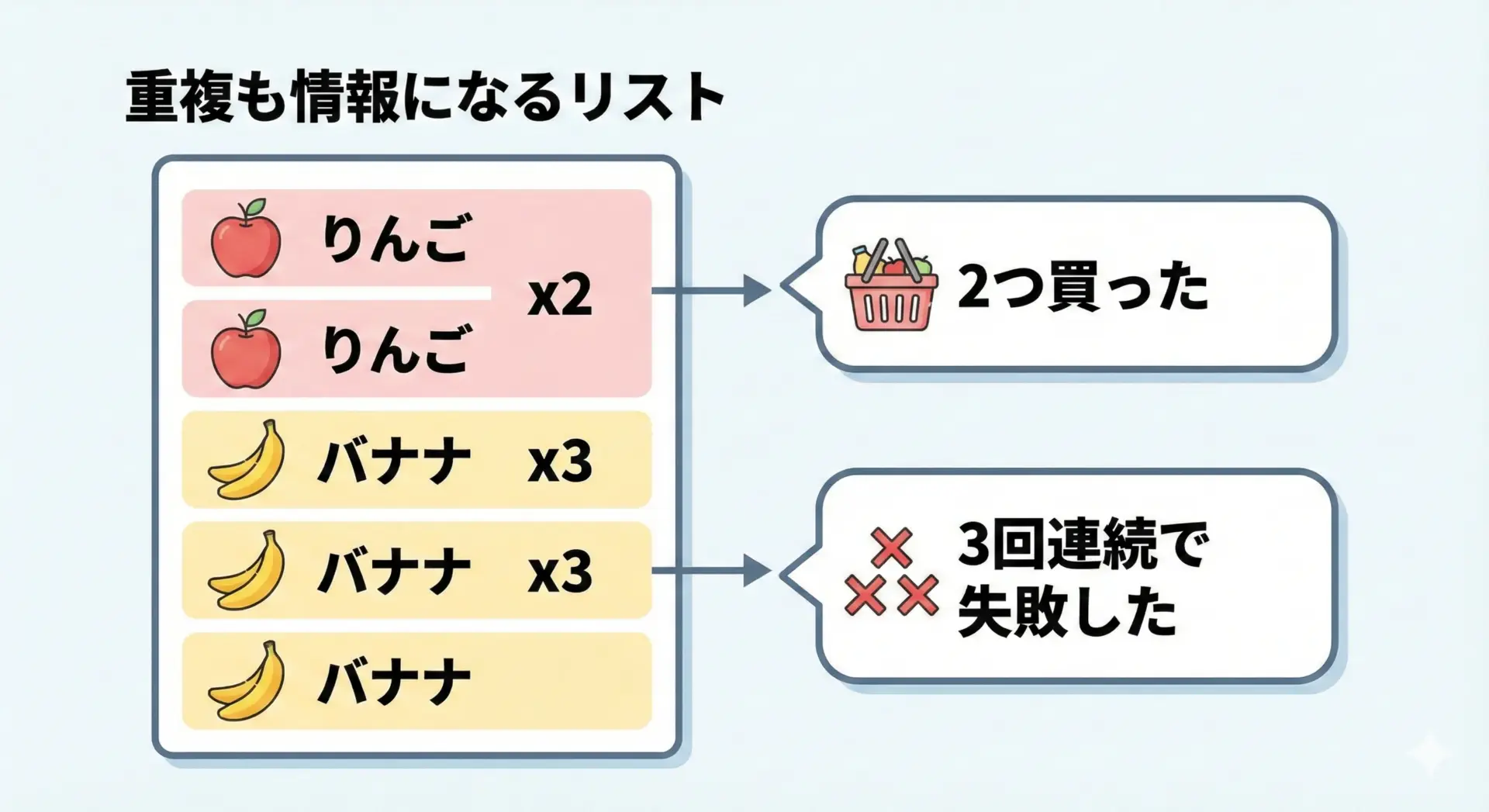
リストとタプルは重複を許しますが、同じ値が複数回出てくること自体に意味がある場合はリストをよく使います。
例えば、購入履歴や投票結果では、同じアイテムが何度も登場することに意味があります。
# 商品の購入履歴(同じ商品を複数回購入している)
purchases = ["apple", "apple", "banana", "banana", "banana"]
# 各商品の購入回数を数える
from collections import Counter
counter = Counter(purchases)
print(counter)Counter({'banana': 3, 'apple': 2})「重複をなくしたくない」「回数や頻度も情報として必要」な場合、setではなくlistを使うべきです。
インデックスでアクセスしたいときのリスト
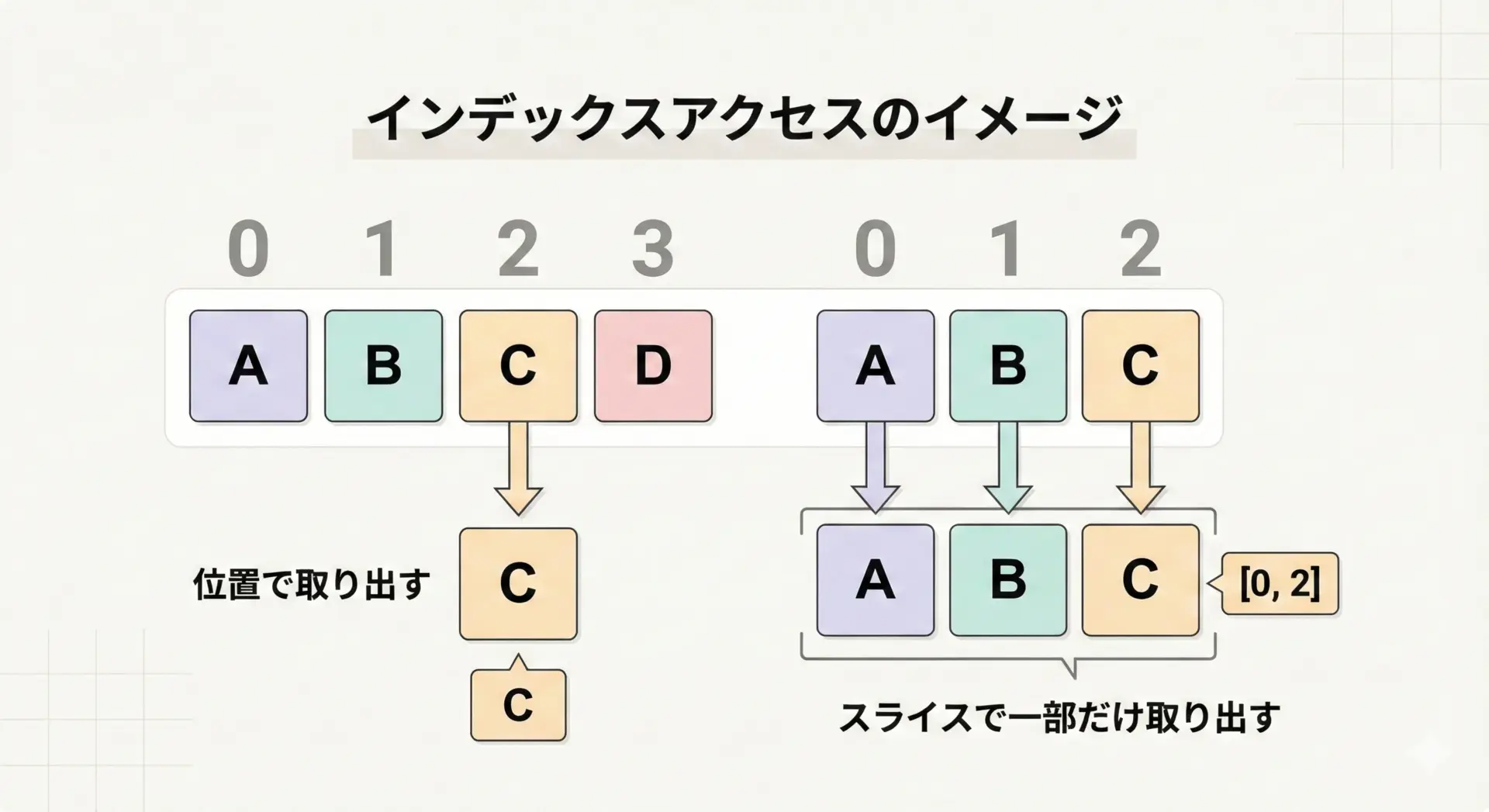
リストの大きな特徴はインデックス番号でのアクセスができることです。
これは、配列的な操作をするうえで非常に重要です。
names = ["Alice", "Bob", "Charlie", "Dave"]
# 2番目の人(0始まりなので index=1)
second = names[1]
# 後ろから2番目
second_last = names[-2]
print("2番目:", second)
print("後ろから2番目:", second_last)2番目: Bob
後ろから2番目: Charlieまた、後で触れるスライスとも相性がよいため、「位置」でデータを扱いたいときはリストを基本として考えます。
ソートやスライスが必要なときのリスト
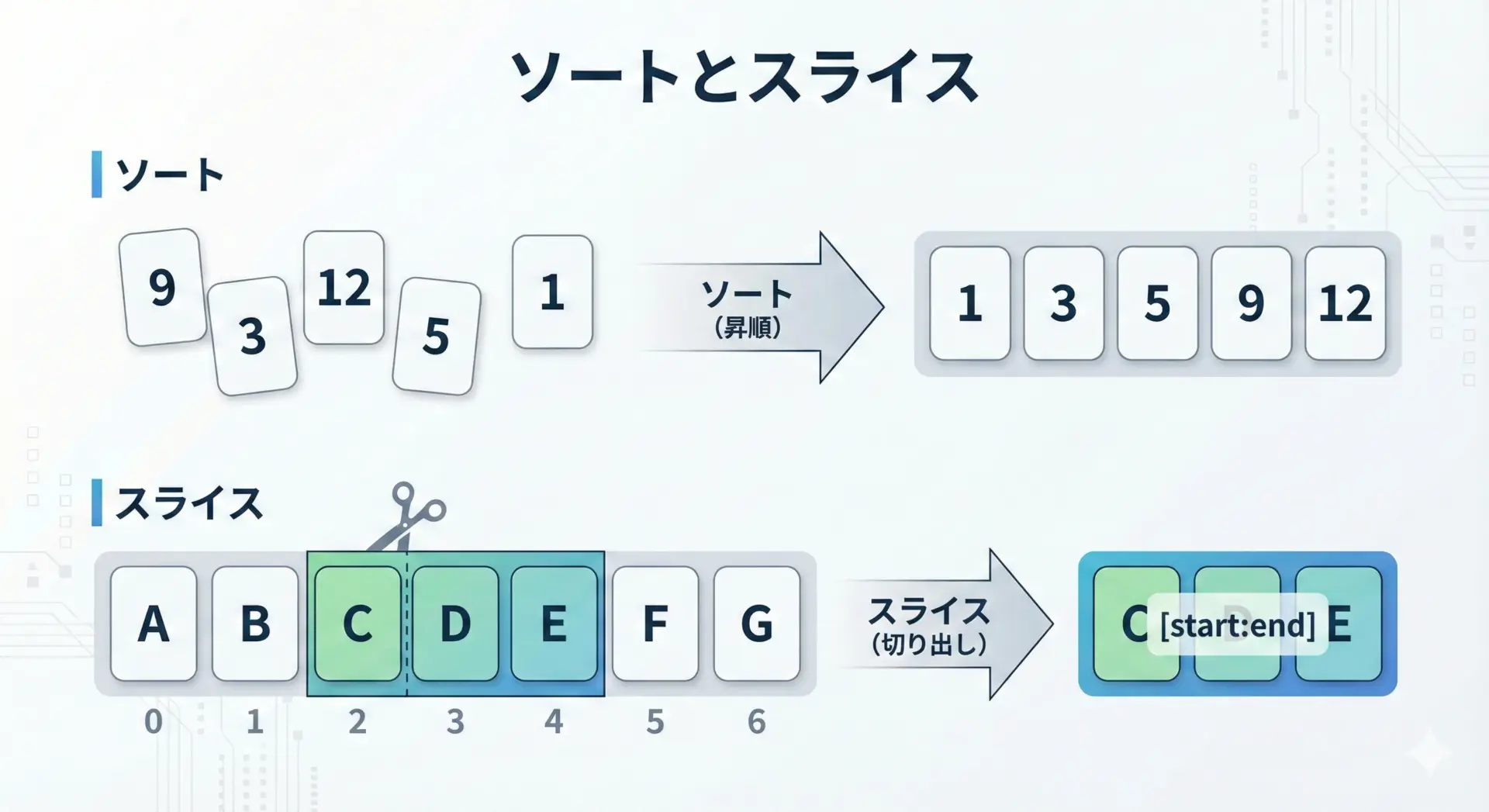
リストはソート(並び替え)やスライス(一部切り出し)を頻繁に行うデータ構造です。
numbers = [5, 2, 9, 1, 5, 6]
# ソート(破壊的: 元のリストを書き換える)
numbers.sort()
print("ソート後:", numbers)
# スライス(非破壊的: 新しいリストを返す)
top3 = numbers[:3] # 先頭3件
print("先頭3件:", top3)ソート後: [1, 2, 5, 5, 6, 9]
先頭3件: [1, 2, 5]タプルでもスライス自体は可能ですが、スライスした結果をさらに加工していくような処理は、リストのほうが自然です。
リストを使うべきでない注意パターン

便利なリストですが、何でもリストにしてしまうと困る場面もあります。
代表的なアンチパターンを挙げます。
1つ目は、順序も重複もいらないのにリストを使うケースです。
# 悪い例: 重複がいらないユーザーIDをリストで保持
user_ids = [100, 101, 102, 100, 103]
# あるIDが含まれるかを調べる(線形探索になる)
if 100 in user_ids:
print("found")このような場合は、setを使うほうが適切です。
重複も排除され、検索も高速になります。
# 良い例: setを使う
user_ids = {100, 101, 102, 100, 103} # 100の重複は自動でなくなる
if 100 in user_ids: # 高速に判定できる
print("found")2つ目は、変更されたくない設定値や定数をリストで持ってしまうケースです。
# 悪い例: 変更されたくない定数をlistで
WEEKDAYS = ["Mon", "Tue", "Wed", "Thu", "Fri"]
# どこかで誤って書き換えてしまうリスクがあるこのような「固定リスト」は、後述するタプルで表現したほうが安全です。
「変わってはいけないものはtuple」と覚えるとよいでしょう。
タプル(tuple)を使うべきパターン
変更されたくないデータはPythonタプルで固定する
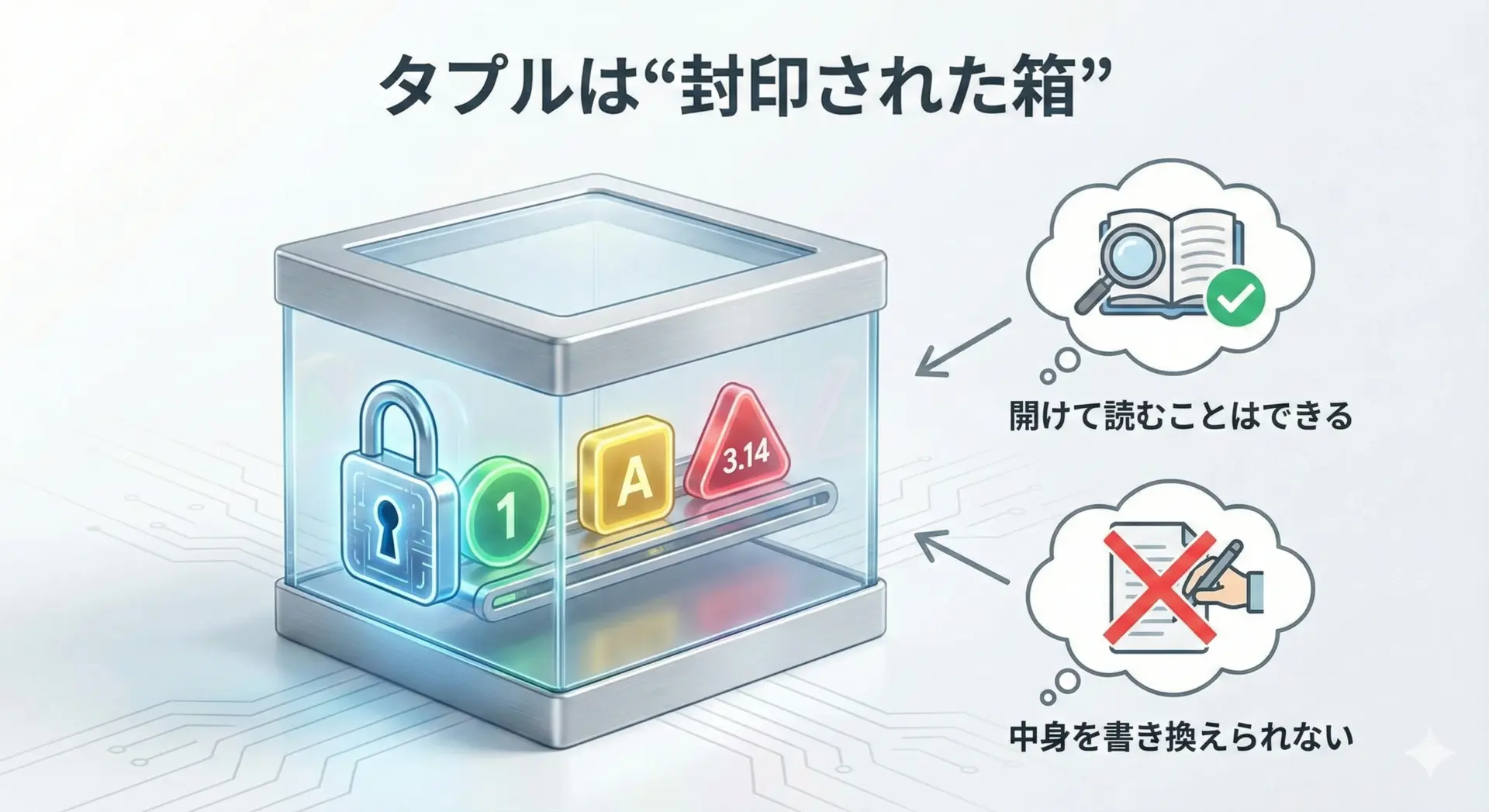
タプルはイミュータブルであることが最大の特徴です。
つまり、一度作ったら中身を書き換えられません。
そのため、次のような場面で活躍します。
- 定数的な設定やマスターデータ
- 「絶対に変えてはならない組み合わせ」の表現
- 外部から渡されたデータを安全に扱いたいとき
# 変更されたくない曜日一覧
WEEKDAYS = ("Mon", "Tue", "Wed", "Thu", "Fri")
# indexアクセスは可能
print(WEEKDAYS[0])
# WEEKDAYS[0] = "Monday" # これはエラーになるMon「誤って変えられるとバグになるようなデータ」はタプルで表すと、設計としても明確になります。
関数の戻り値で複数値を返すときのタプル
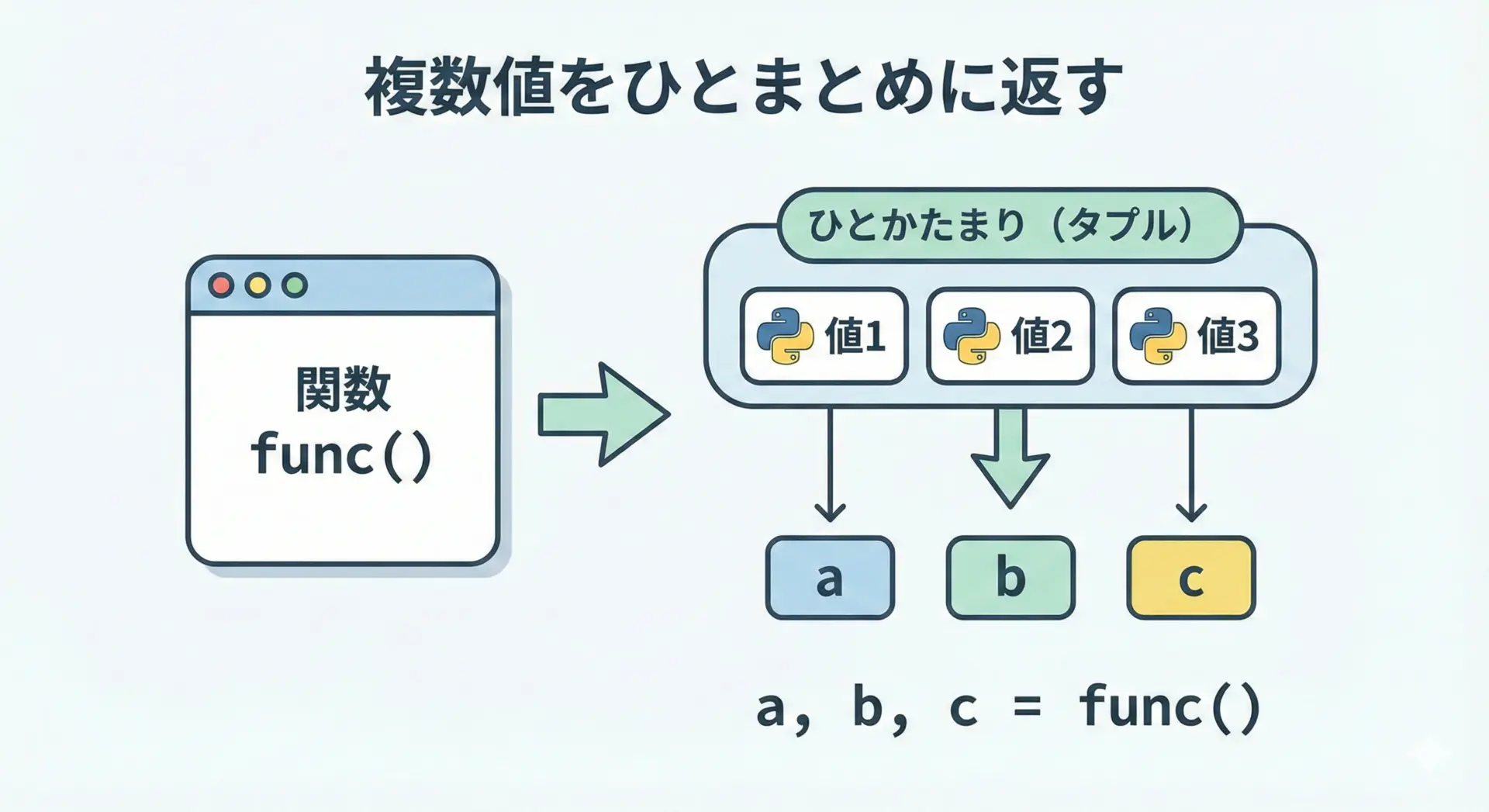
Pythonでは、関数から複数の値を返すとき、暗黙的にタプルが使われます。
def calc_stats(nums):
"""数値リストの合計、平均、件数を返す関数"""
total = sum(nums)
count = len(nums)
avg = total / count if count > 0 else 0
# タプルで返す
return total, avg, count
numbers = [1, 2, 3, 4]
# 受け取り側ではタプルのアンパックを使う
total, avg, count = calc_stats(numbers)
print("合計:", total)
print("平均:", avg)
print("件数:", count)合計: 10
平均: 2.5
件数: 4return total, avg, count は実際には (total, avg, count)
「ひとかたまりの結果」を返すときにはタプルが自然です。
辞書キーに使うならリストではなくタプル
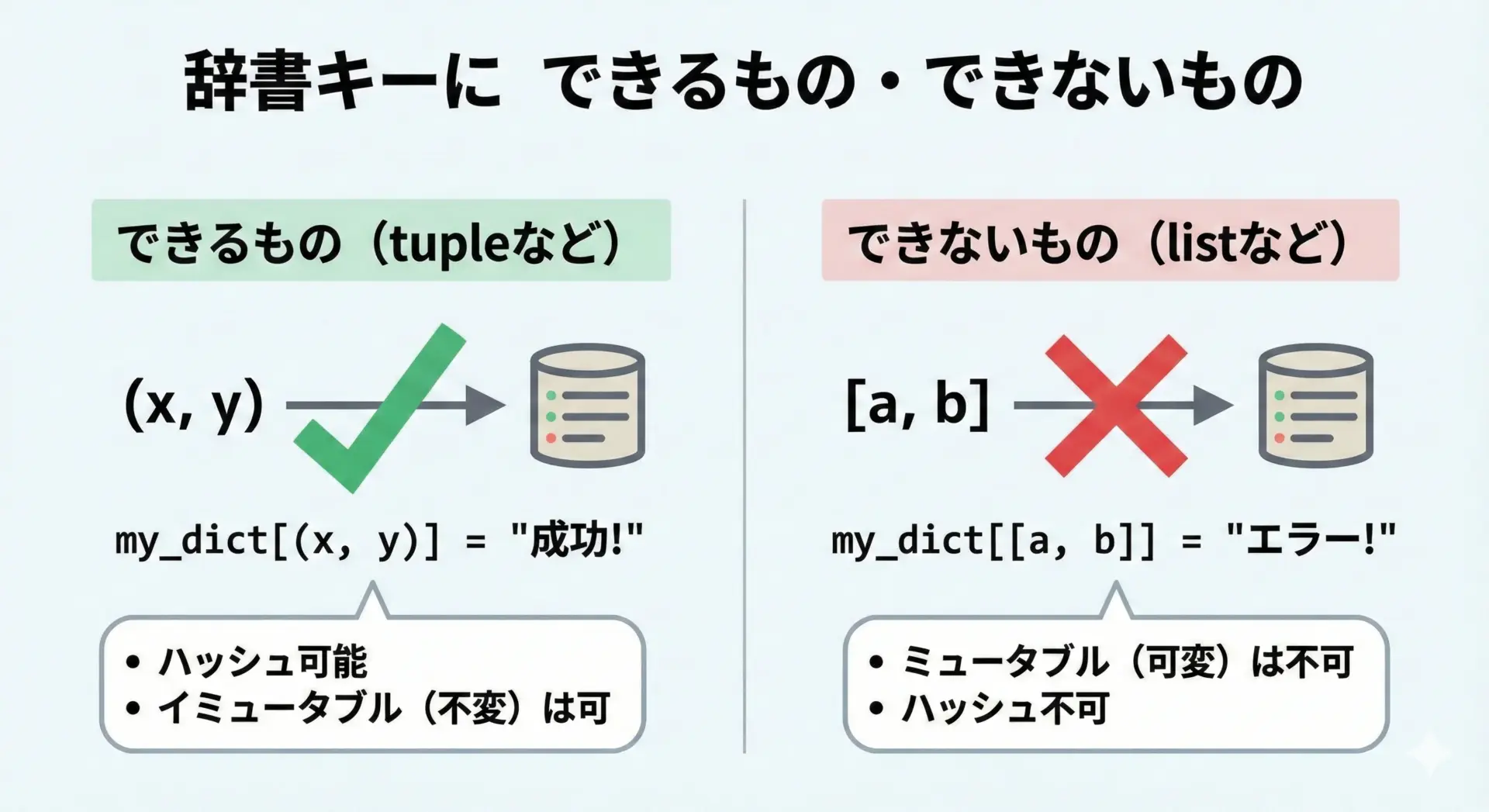
辞書(dict)のキーには、イミュータブルでハッシュ可能なオブジェクトしか使えません。
そのため、リストはキーにできず、タプルはキーにできます。
座標や複数の条件をキーにしたいときにタプルはよく使われます。
# (x, y) 座標をキーにした辞書
grid = {}
grid[(0, 0)] = "start"
grid[(1, 2)] = "tree"
print(grid[(1, 2)])
# 下はエラー: listはdictのキーにできない
# bad_key = [0, 0]
# grid[bad_key] = "start" # TypeErrortree「複数の値の組み合わせ」を辞書キーにしたいときには、必ずタプルを使います。
構造が決まったレコードデータにタプルを使う
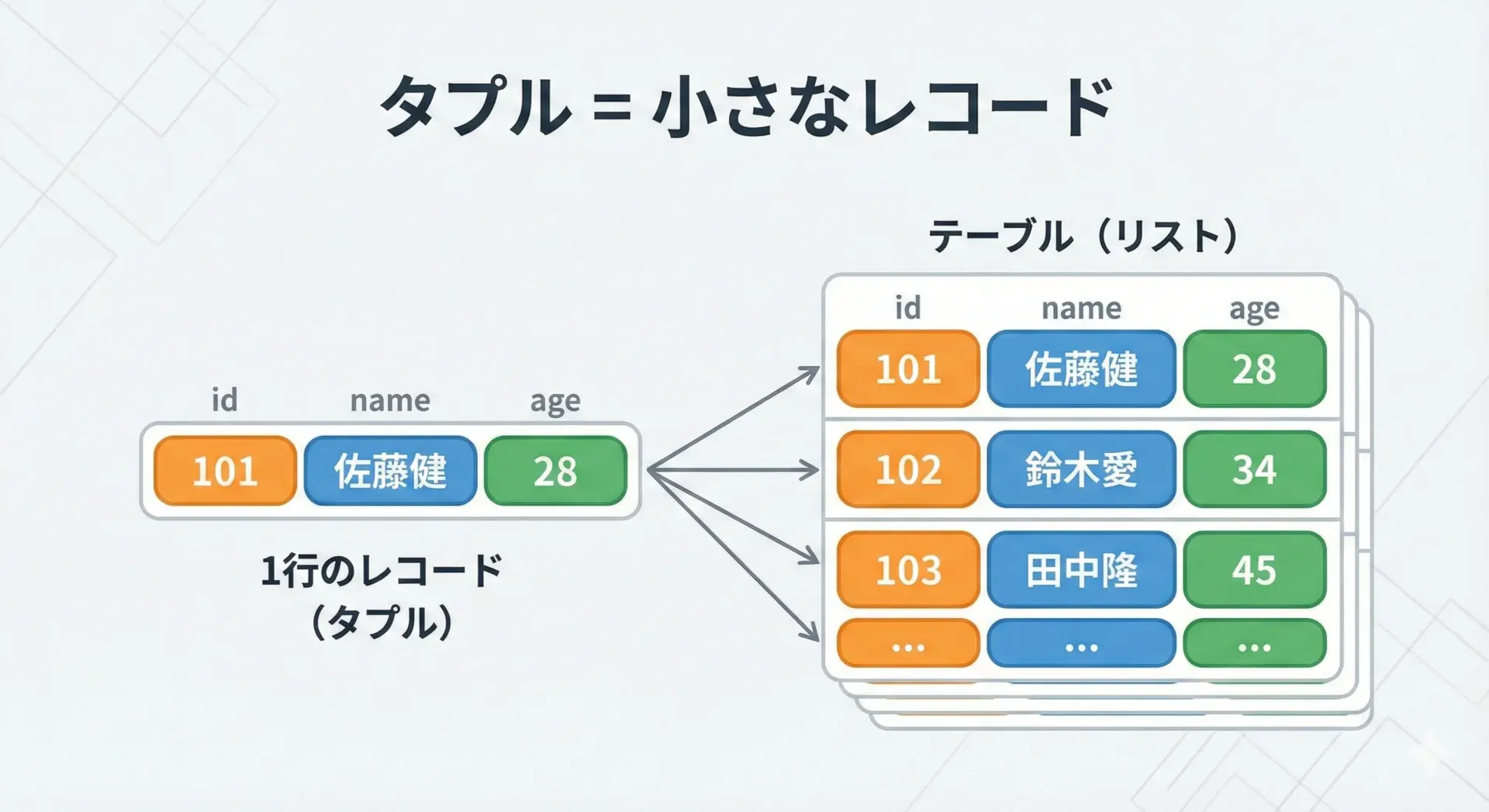
タプルは、「固定された構造を持つひとつのレコード」を表現するのに向いています。
例えば、ユーザーの情報を (id, name, age)
# 1人分のユーザーレコード: (id, name, age)
user1 = (1, "Alice", 30)
user2 = (2, "Bob", 25)
# レコードの一覧は「タプルのリスト」にするパターンが多い
users = [user1, user2]
for user in users:
user_id, name, age = user # アンパックで展開
print(f"id={user_id}, name={name}, age={age}")id=1, name=Alice, age=30
id=2, name=Bob, age=25「フィールド数も順番も事前に決まっていて変わらないデータ」はタプルで表すと、意図が明確になります。
タプルとリストのどちらを選ぶかの判断基準
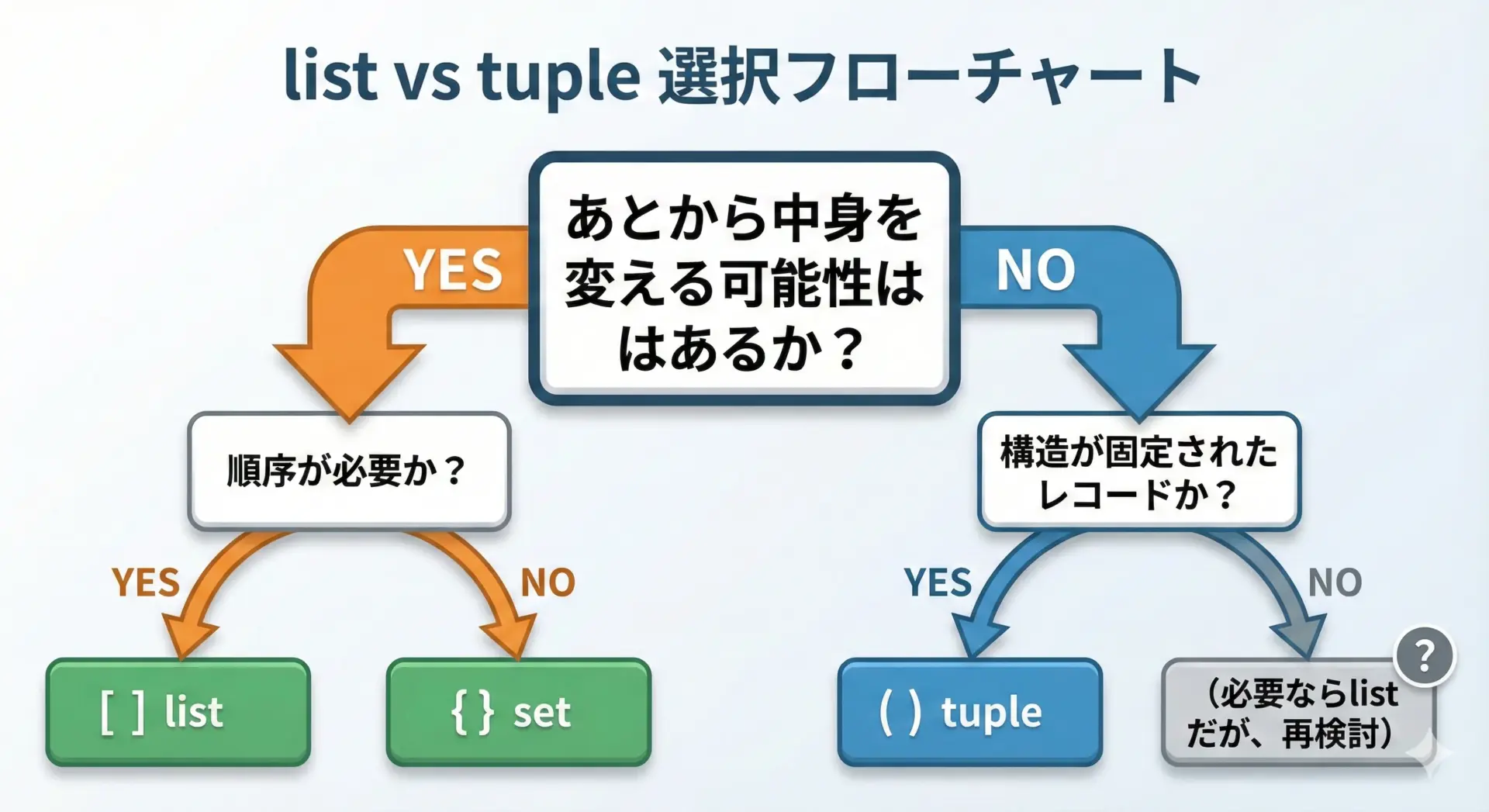
リストとタプルで迷ったときは、次の問いを順番に考えると判断しやすくなります。
- あとから中身を変える必要があるか?
- ある → list
- ない → 2へ
- 固定された「ひとかたまり」や「レコード」を表現したいか?
- そう → tuple
- そうでもない → list(ただし、本当に変えなくてよいのか再検討)
まとめると、以下のように言えます。
- 「変化する配列」= list
- 「固定された組」= tuple
これを基本方針としておくと、コレクション選びで迷うことが少なくなります。
セット(set)を使うべきパターン
重複を自動で排除したいときのPythonセット
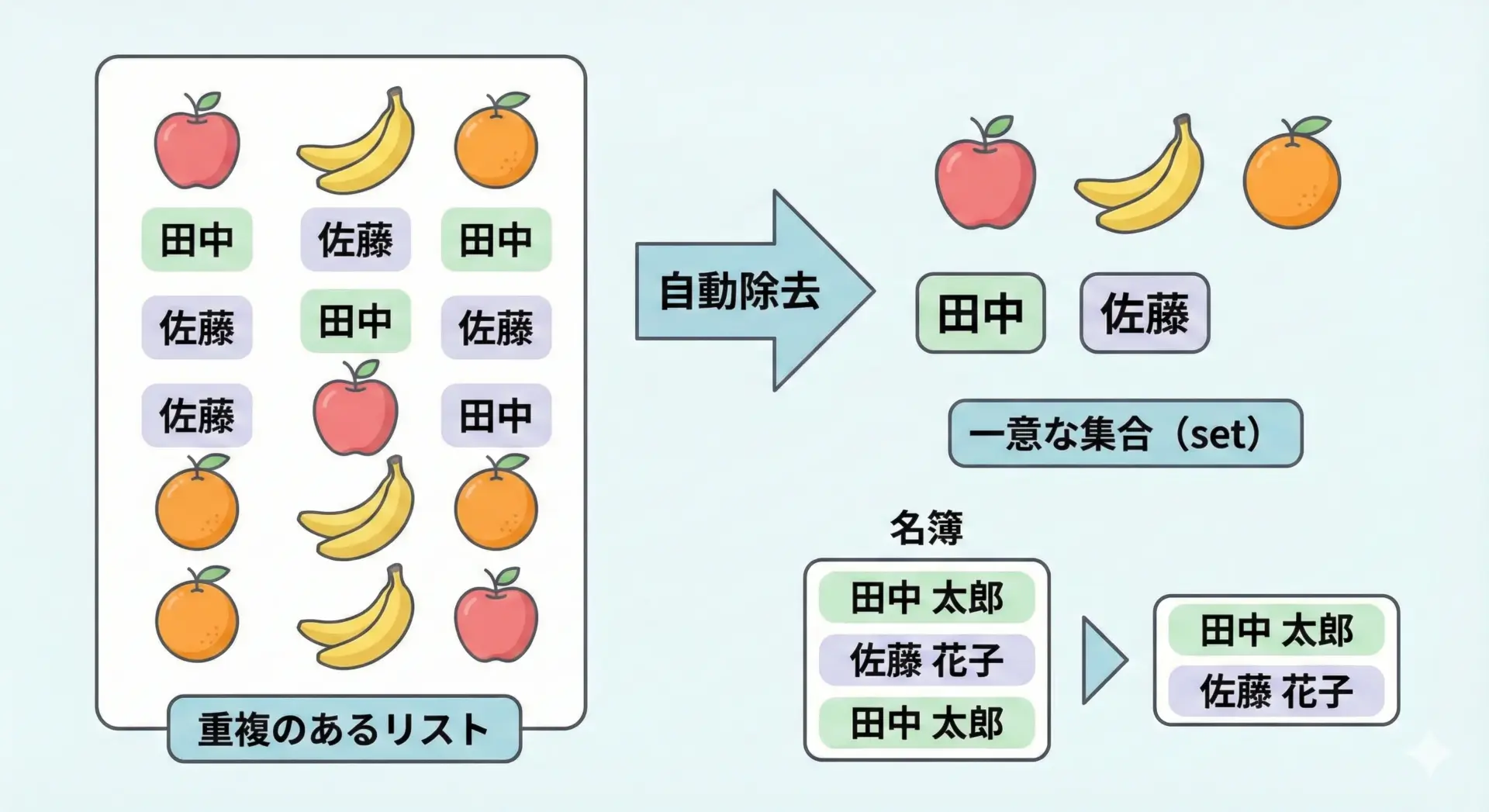
セットは「順序なし・重複なし」のコレクションです。
特に、重複した要素を自動で取り除いてくれる点が特徴的です。
# 重複を含むリスト
tags = ["python", "web", "python", "ai", "web"]
# set に変換すると重複が消える
unique_tags = set(tags)
print(unique_tags){'python', 'ai', 'web'}順序は保証されませんが、「一度でも出てきたことがあるか」を知りたい場合には非常に便利です。
集合演算(和・積・差)を使った効率的なデータ処理
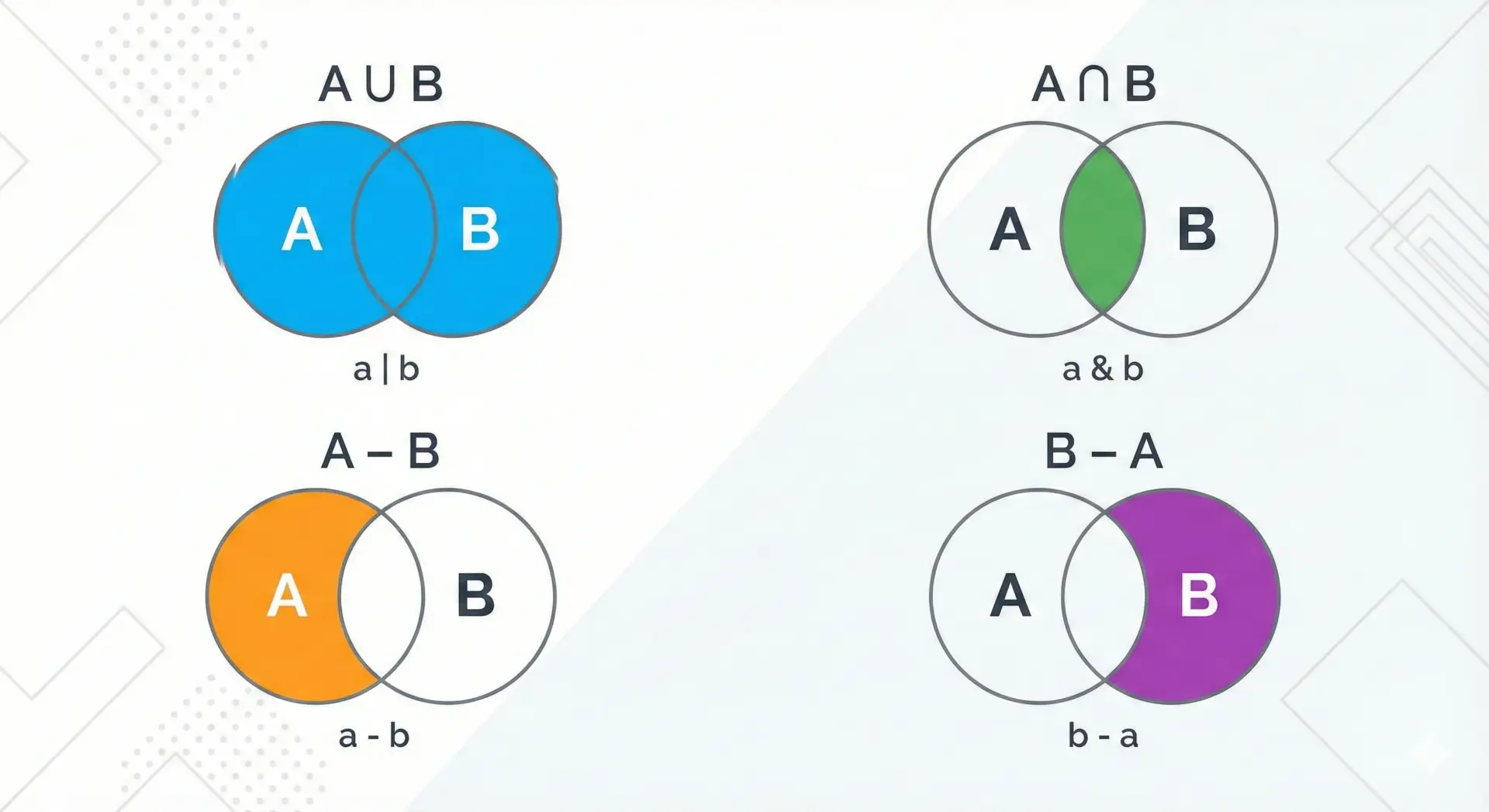
setが真価を発揮するのは、集合演算(和・積・差など)を使ったデータ処理です。
Pythonのsetでは、以下のような演算が用意されています。
| 演算 | 記号 | メソッド | 意味 |
|---|---|---|---|
| 和集合 | a \| b | a.union(b) | 両方に含まれる全要素 |
| 積集合 | a & b | a.intersection(b) | 両方に共通する要素のみ |
| 差集合 | a - b | a.difference(b) | aにあってbにない要素 |
| 対称差 | a ^ b | a.symmetric_difference(b) | どちらか一方にだけある要素 |
具体例を見てみます。
a = {"apple", "banana", "orange"}
b = {"banana", "grape", "orange"}
print("和集合:", a | b)
print("積集合:", a & b)
print("差集合(a-b):", a - b)
print("対称差:", a ^ b)和集合: {'banana', 'orange', 'grape', 'apple'}
積集合: {'banana', 'orange'}
差集合(a-b): {'apple'}
対称差: {'grape', 'apple'}「2つの集合の共通部分」「片方だけに存在する要素」などを求める処理は、setを使うと非常にシンプルで効率的に書けます。
メンバーシップテストを高速化したいときのセット
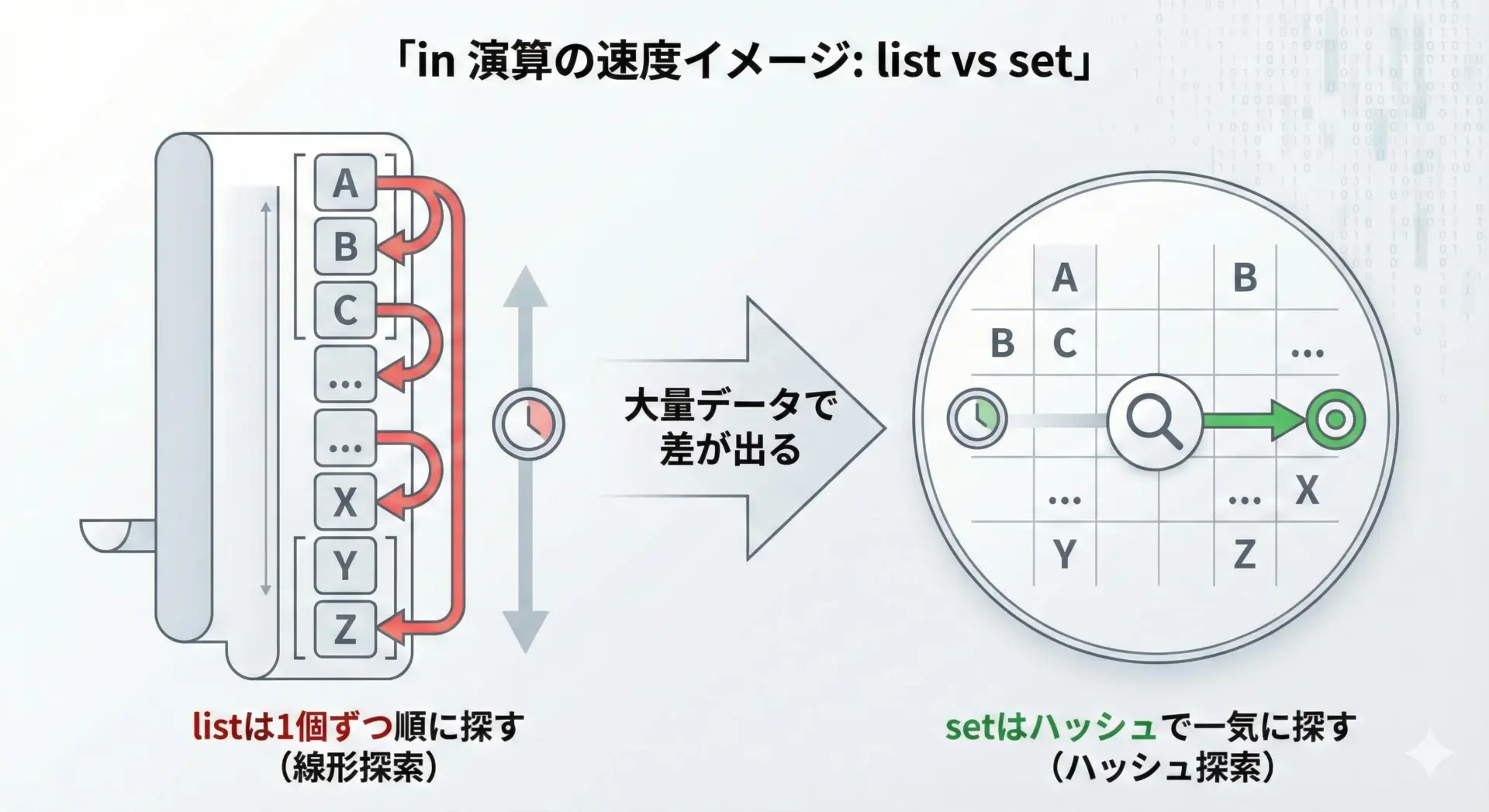
setのもう一つの大きな利点は、要素が含まれているか(in演算)の判定が高速なことです。
# 大量のIDから、「すでに処理済みか」を調べるケース
processed_ids = {1001, 1002, 1003, 1004} # setで保持
target_id = 1003
if target_id in processed_ids:
print("すでに処理済みです")すでに処理済みですリストで同じことをすると、要素数Nに対して最悪O(N)の時間がかかりますが、setなら平均してO(1)程度です。
「大量データの中に含まれるかどうかを何度も調べる」ときは、setを強く検討すべきです。
リストから重複削除するときのセット活用パターン
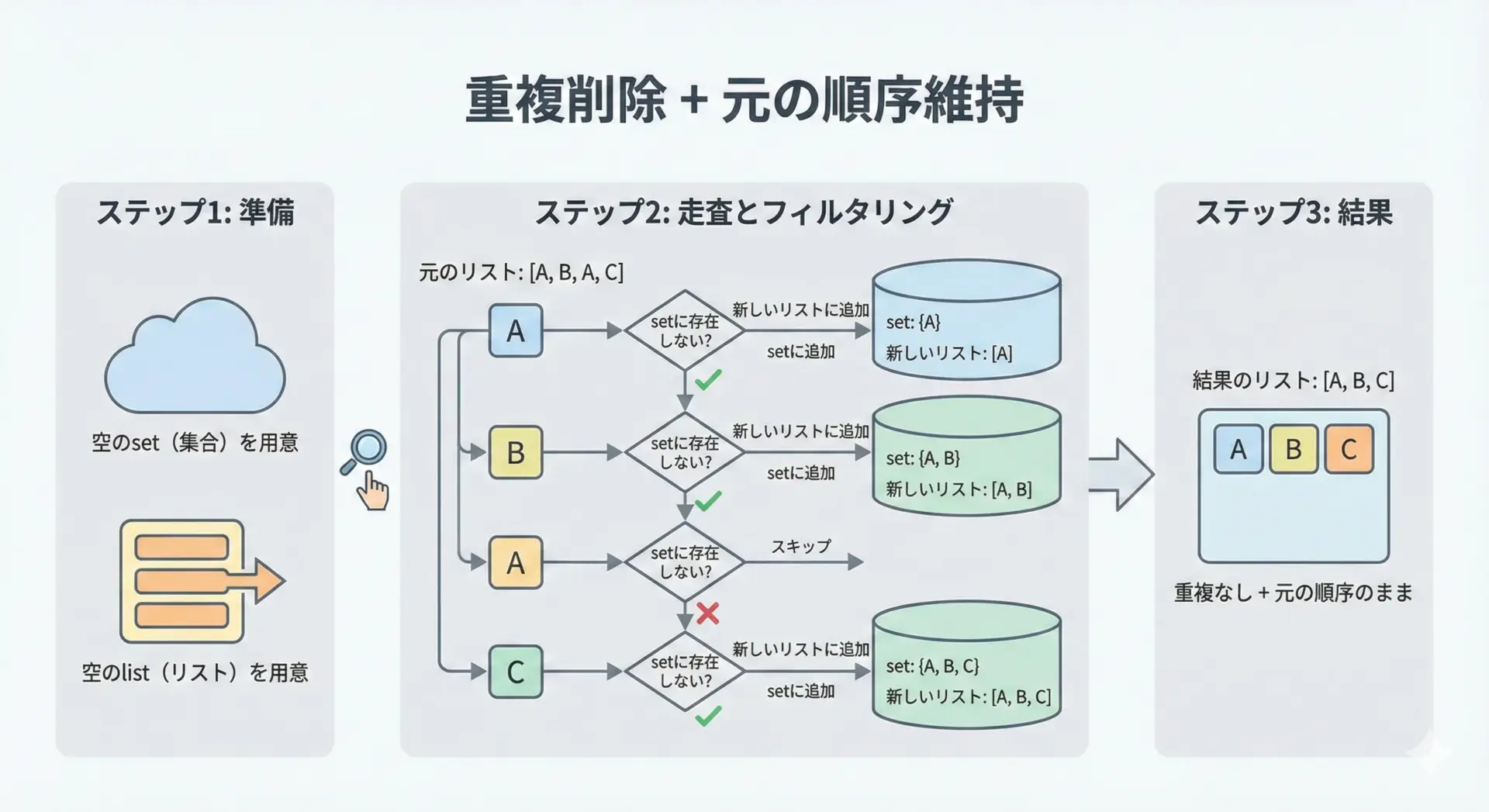
setは重複を自動で取り除いてくれますが、そのまま使うと元の順序が失われるという問題があります。
順序を維持しつつ重複だけを消したい場合は、次のようなパターンが定番です。
def unique_preserve_order(seq):
"""順序を保ったまま重複を削除した新しいリストを返す"""
seen = set()
result = []
for item in seq:
if item not in seen:
seen.add(item)
result.append(item)
return result
items = ["a", "b", "a", "c", "b", "d"]
unique_items = unique_preserve_order(items)
print(unique_items)['a', 'b', 'c', 'd']このように「見たことがあるかどうか」の管理だけをsetに任せることで、順序を保った重複削除が実現できます。
セットを使うと困るケースと注意点
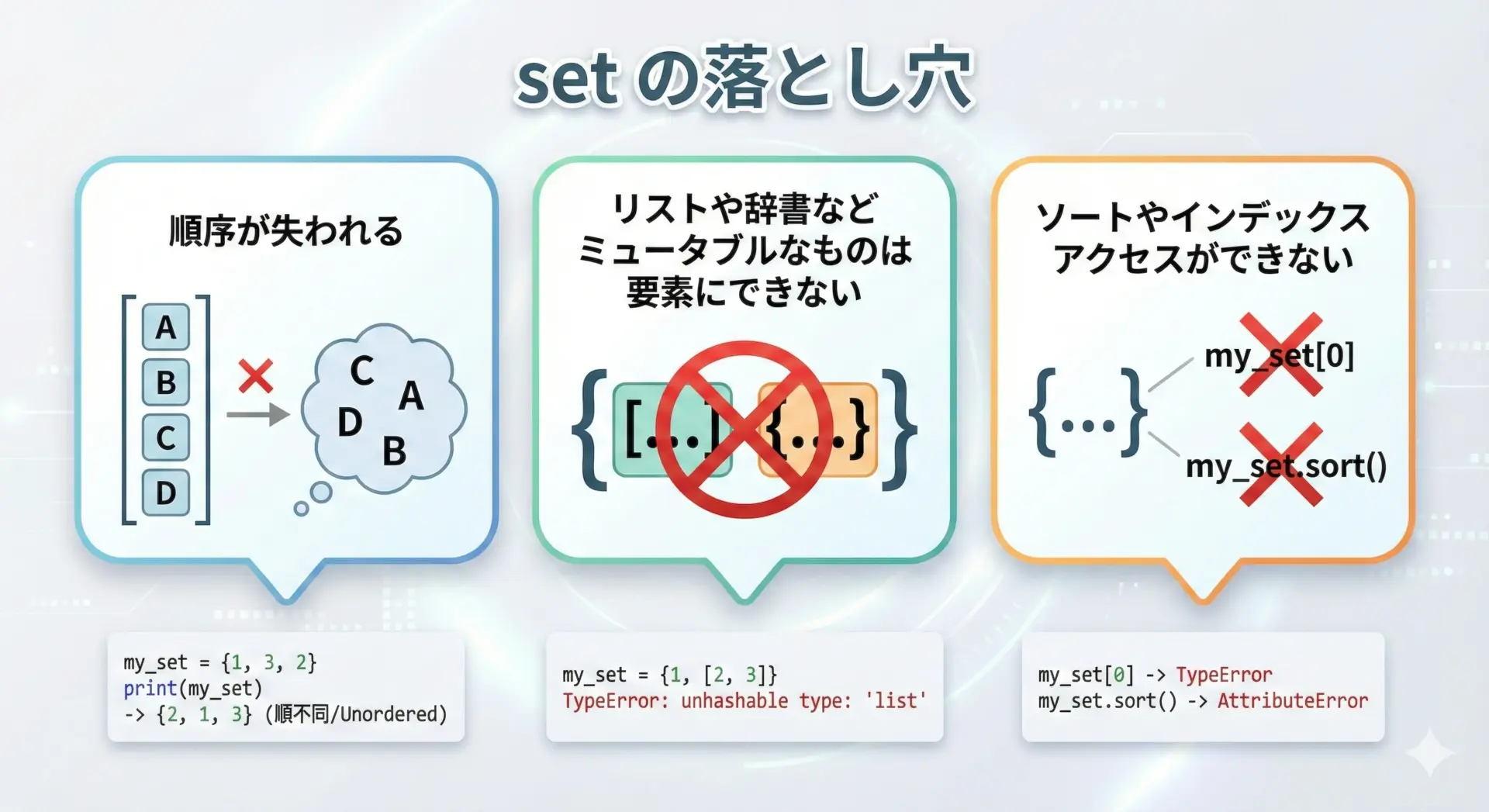
setには便利な点が多い一方で、使うと困るケースもあります。
代表的な注意点を挙げます。
1つ目は、順序が失われることです。
numbers = [1, 3, 2, 4]
s = set(numbers)
print(s) # 並び順は保証されない{1, 2, 3, 4}表示結果の順序は環境によって変わる可能性があります。
順番に意味があるデータにsetを使ってはいけません。
2つ目は、ミュータブルなオブジェクト(リストや辞書など)は要素にできないことです。
setの要素はハッシュ可能である必要があるためです。
# NG例: listを要素にしようとするとエラー
# bad_set = {[1, 2], [3, 4]} # TypeError
# OK例: tupleなら要素にできる
good_set = {(1, 2), (3, 4)}
print(good_set){(1, 2), (3, 4)}3つ目は、インデックスアクセスやソートが直接はできないことです。
必要であれば、一度リストなどに変換してから操作します。
s = {3, 1, 4, 2}
# ソートされたリストに変換してから使う
sorted_list = sorted(s)
print(sorted_list)
print(sorted_list[0]) # 最小値[1, 2, 3, 4]
1「順序が必要」「ミュータブルを扱いたい」「インデックスでアクセスしたい」といった場合には、setは向いていないと覚えておきましょう。
まとめ
リスト・タプル・セットは、見た目が似ていても性格は大きく異なります。
「順序が必要か」「中身を変えるか」「重複を許すか」の3点を意識すれば、選ぶべきコレクションはかなり明確になります。
変化する並びにはlist、固定された組にはtuple、一意な集合や高速検索にはsetと役割を整理しておくことで、コードの意図が伝わりやすく、バグも減らせます。
日々の実装で「これ、本当にlistでいい?」と一度立ち止まり、最適なコレクションを選ぶ習慣を身につけていきましょう。

