Pythonでは/と//という2種類の割り算演算子があり、見た目が似ているため混乱しやすいです。
しかし、両者は結果の型や小数点以下の扱いが大きく異なります。
本記事では、「Pythonの割り算の挙動」と「正しい切り捨ての書き方」を、図解とサンプルコードを用いて丁寧に解説していきます。
Pythonの割り算演算子の基本
/と//の違いを一言でいうと

一言でいうと、/は「小数も含めた真の割り算」、//は「結果を切り捨てる割り算」です。
もう少し丁寧に説明すると、次のようになります。
/演算子
割り算の結果を必ず浮動小数点数(float)として返します。整数同士でも小数が返ります。//演算子
割り算の結果を切り捨てた値として返します。オペランドが整数だけならint、片方でもfloatならfloatになるという特徴があります。
Python2とPython3での割り算の違い
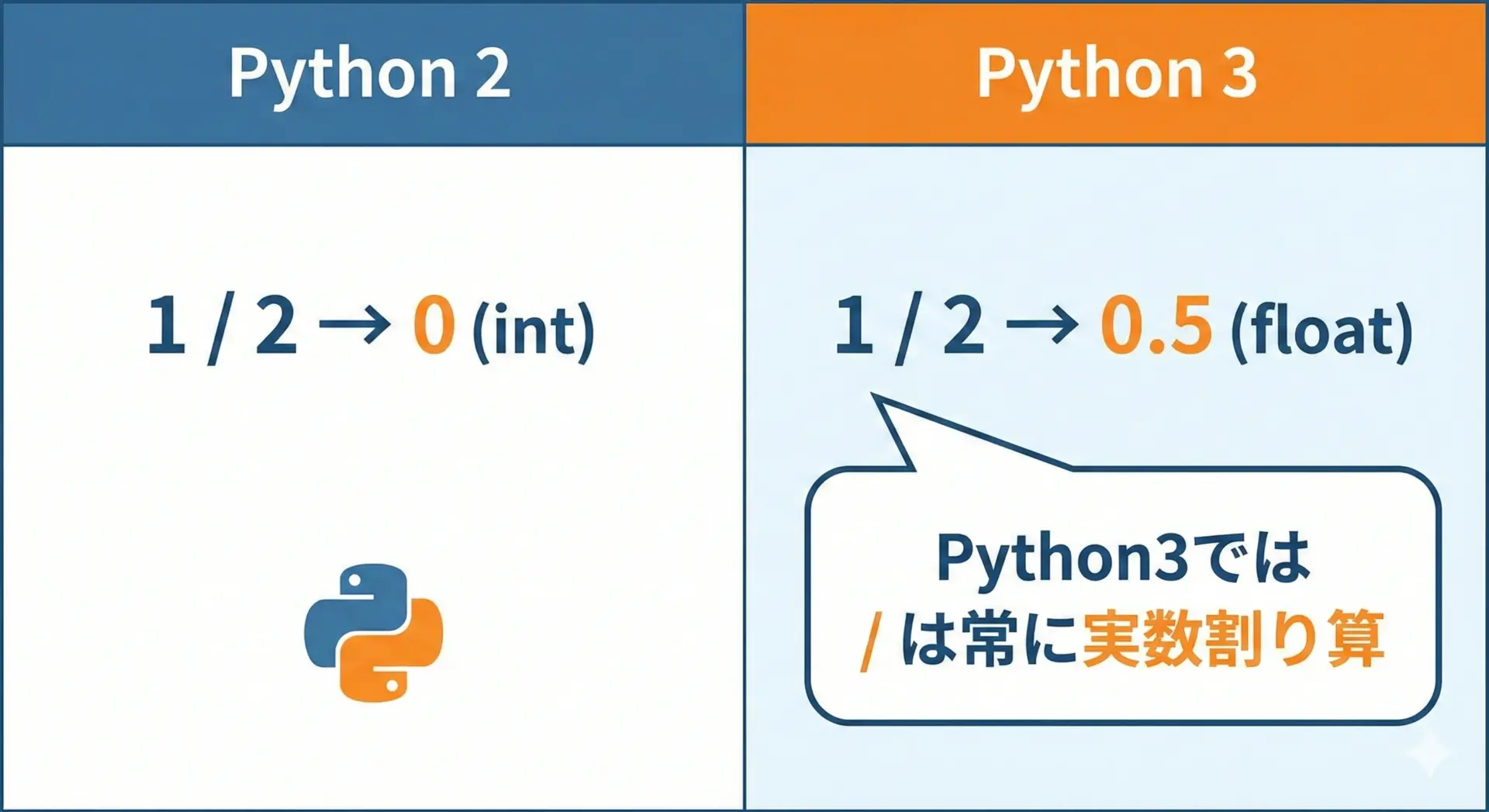
Pythonのバージョンによって/の挙動が異なる点は、古い記事を読むときによく引っかかるポイントです。
- Python2
1 / 2のように整数同士で割り算をすると、整数除算となり0が返っていました。 - Python3
常に「真の割り算」となり、1 / 2は0.5を返します。整数で割っても必ずfloatです。
現在主流のPython3では、/は常に小数まで計算するので、//を使わない限り「勝手に切り捨てられる」ということはありません。
intとfloatで結果がどう変わるか
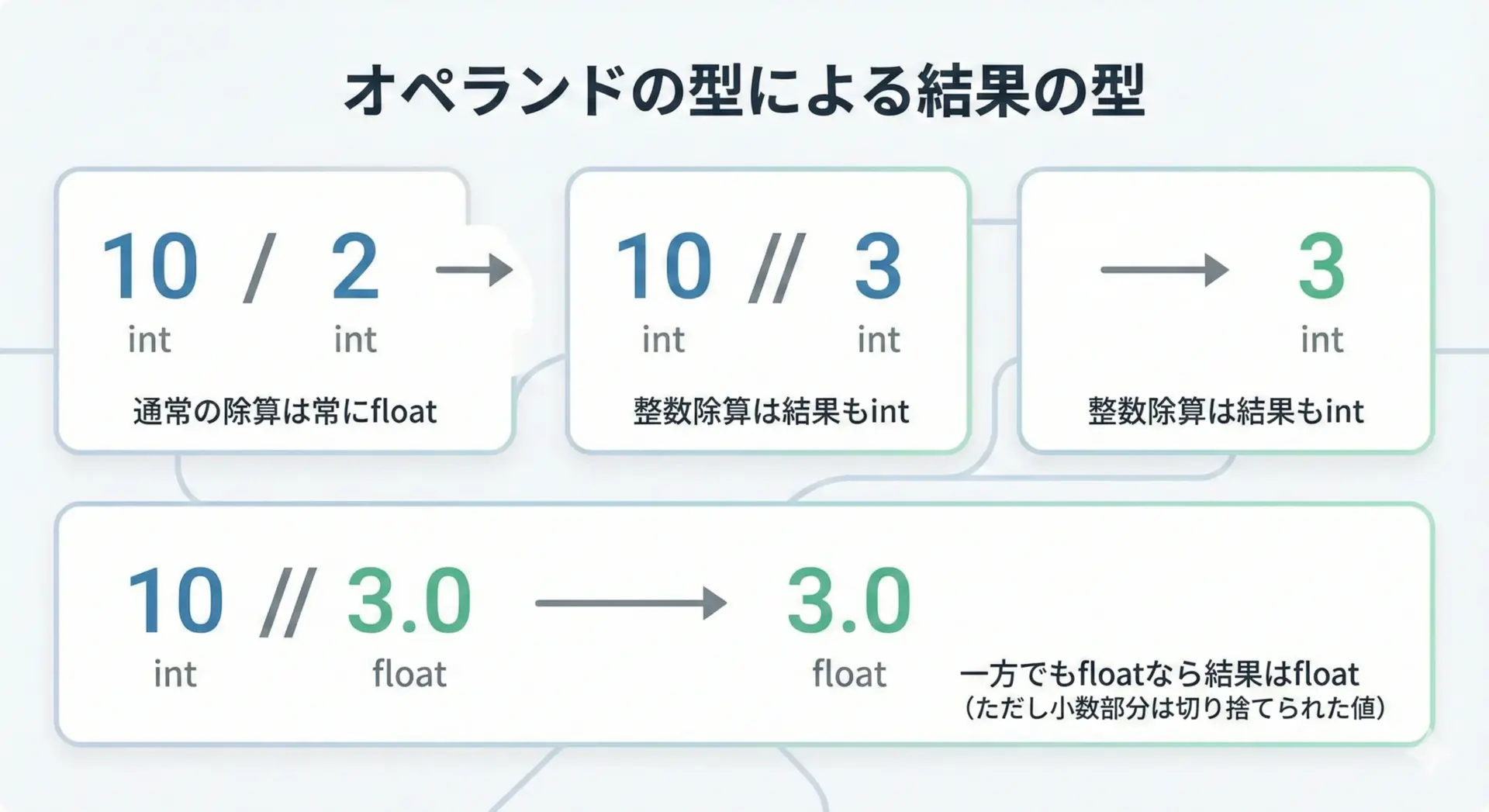
Pythonでは/と//のどちらでも、オペランド(左右の値)の型によって結果の型が少し変わります。
代表的な例を表にまとめます。
| 式 | 内容 | 結果 |
|---|---|---|
5 / 2 | 真の割り算(int / int) | 2.5 (float) |
5.0 / 2 | 真の割り算(float / int) | 2.5 (float) |
5 // 2 | 切り捨て除算(int // int) | 2 (int) |
5.0 // 2 | 切り捨て除算(float // int) | 2.0 (float) |
-5 // 2 | 負数を含む切り捨て除算 | -3 (int) |
サンプルコードで確認してみます。
# / と // の結果と型を確認するサンプル
values = [
("5 / 2", 5 / 2),
("5.0 / 2", 5.0 / 2),
("5 // 2", 5 // 2),
("5.0 // 2", 5.0 // 2),
("-5 // 2", -5 // 2),
]
for expr, result in values:
print(f"{expr:8} = {result!r:6} (type: {type(result).__name__})")5 / 2 = 2.5 (type: float)
5.0 / 2 = 2.5 (type: float)
5 // 2 = 2 (type: int)
5.0 // 2 = 2.0 (type: float)
-5 // 2 = -3 (type: int)「// だから常にint」というわけではないことに注意してください。
片方でもfloatなら、//でもfloatになります。
/演算子(真の割り算)の挙動
/の基本的な使い方と戻り値の型
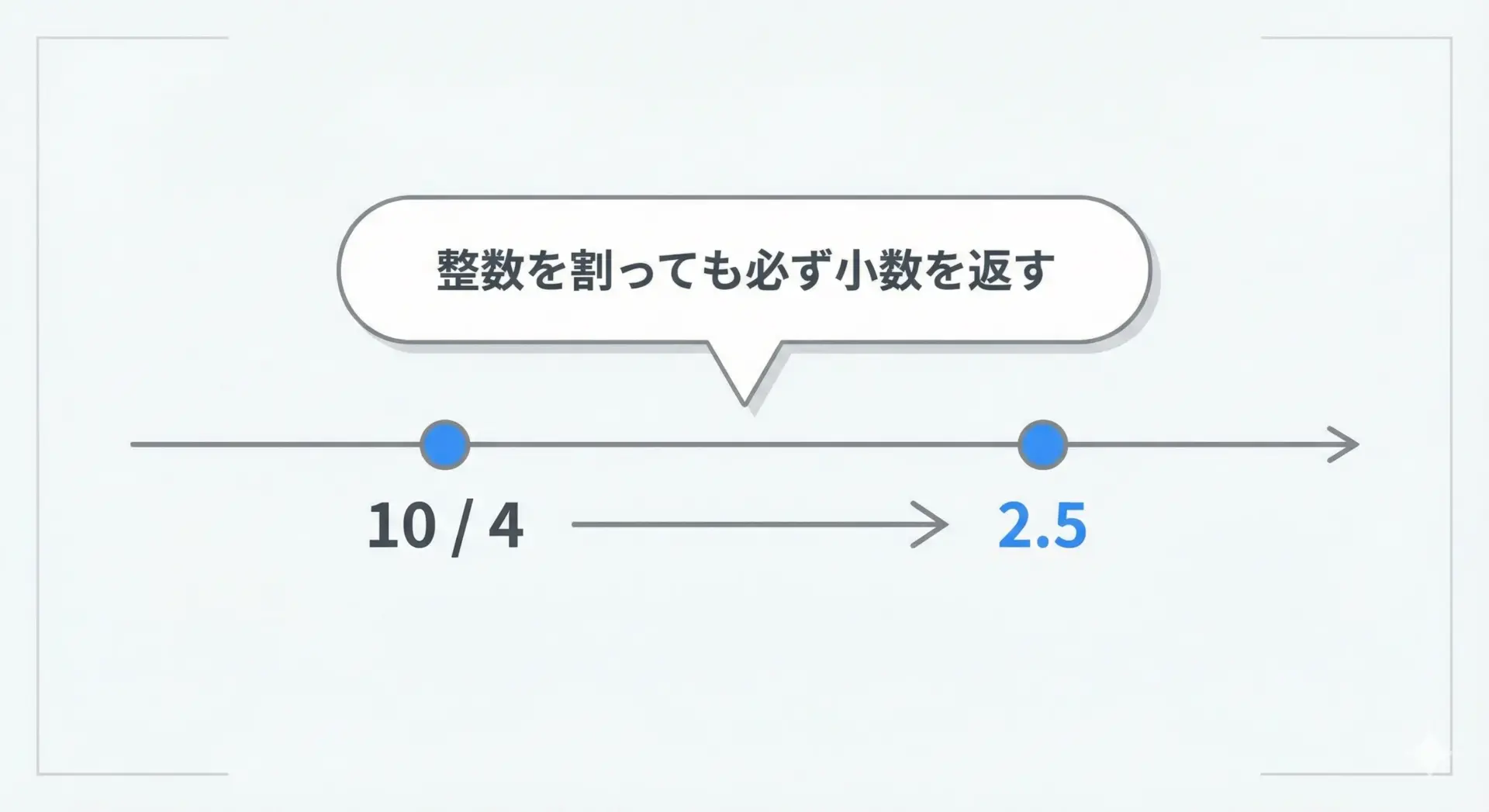
/演算子は「真の割り算(true division)」です。
Python3では、整数同士を割っても必ずfloatが返ります。
a = 10
b = 4
result = a / b
print("10 / 4 =", result)
print("type:", type(result))10 / 4 = 2.5
type: <class 'float'>このように、aもbもintですが、結果は2.5というfloatになります。
整数同士の/で小数が返る理由
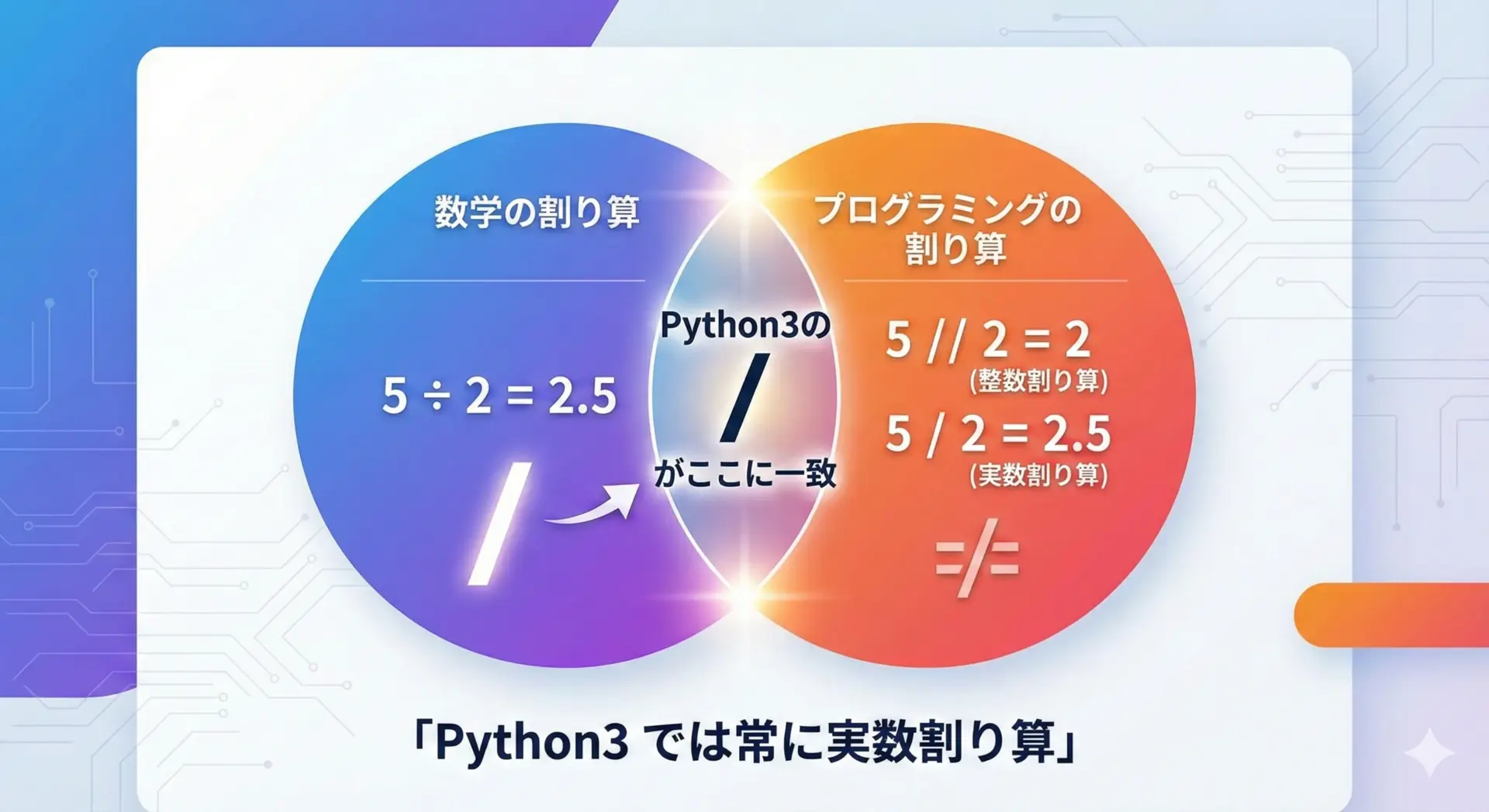
Python3では、数学で習う割り算と同じ結果を返すことを目指して設計されています。
そのため、次のような計算では、昔の言語(Cや一部の他言語)と挙動が異なります。
print(7 / 3) # どんな値になるでしょう?
print(1 / 2)2.3333333333333335
0.5このように/は「割り算の結果をできるだけ正確に表す」ことを優先しているため、必ずfloatで返すという仕様になっています。
負の数を含む/の注意点
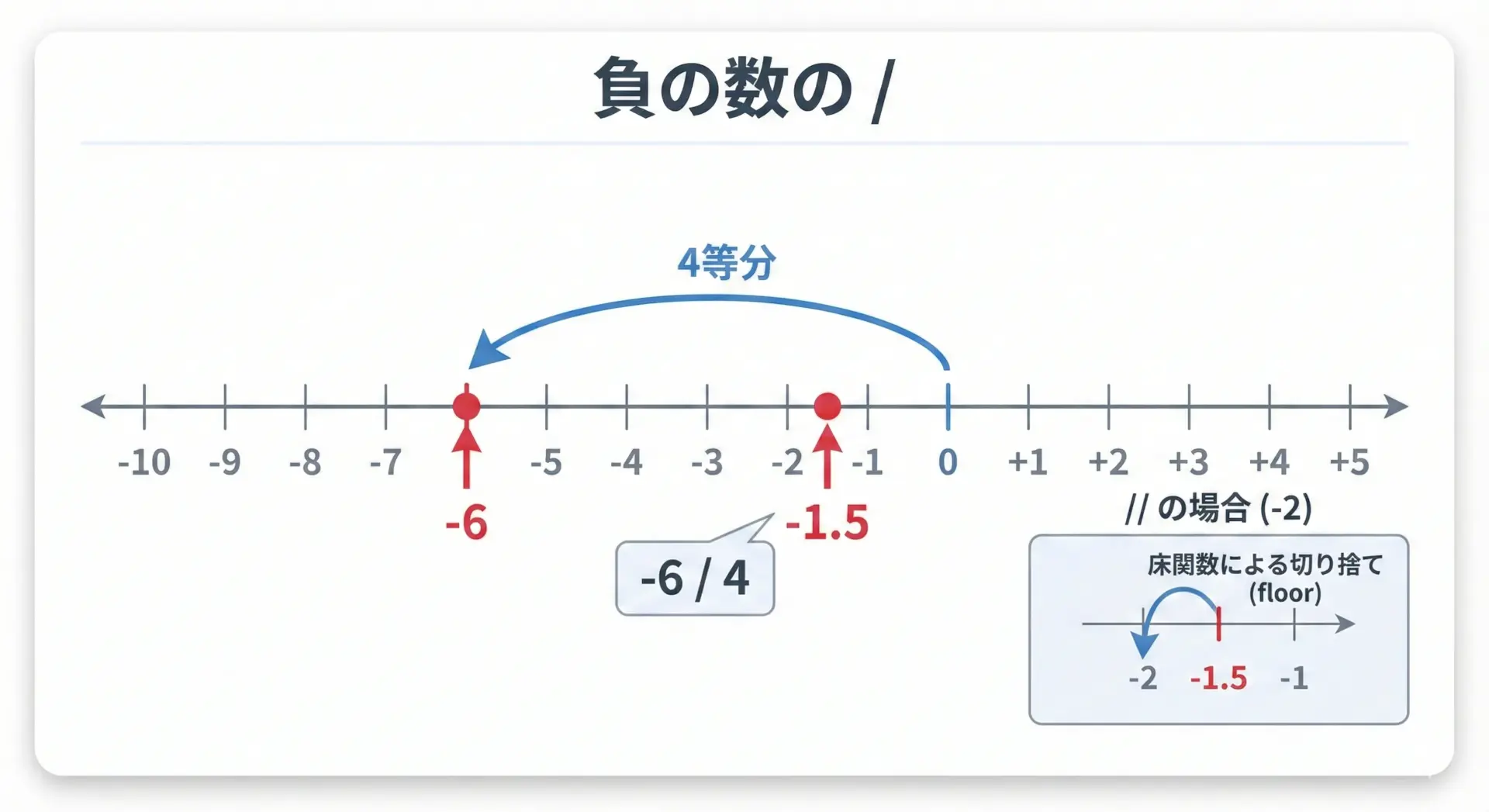
/の場合は、正の数でも負の数でも「ふつうの割り算」を行います。
つまり、単純に数値を割るだけです。
print(-6 / 4)
print(6 / -4)
print(-6 / -4)-1.5
-1.5
1.5負の数を含むとややこしくなるのは//側なので、/については「常に数学通り」と覚えておいて問題ありません。
小数点以下の桁数を揃える書き方
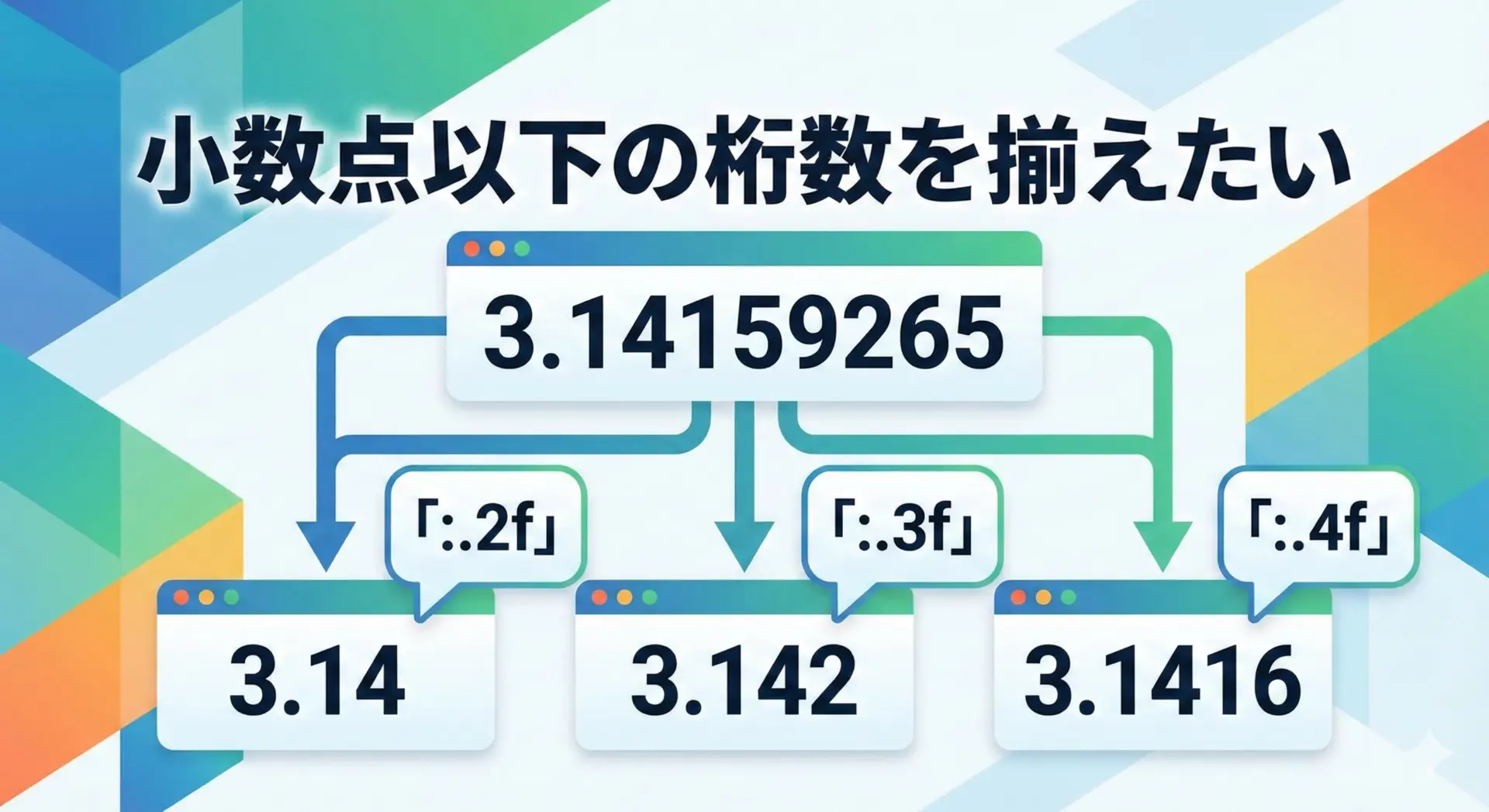
/で割り算すると、必要に応じて長い小数が返ることがあります。
そのまま表示すると読みにくいので、表示用に桁数をそろえることがよくあります。
代表的な方法は次の3つです。
x = 10 / 3 # 3.3333... が入る
# 1. f文字列で小数点以下2桁に丸めて表示
print(f"{x:.2f}") # → '3.33'
# 2. format関数を使う
print(format(x, ".3f")) # → '3.333'
# 3. round関数で丸めてから表示
print(round(x, 2)) # → 3.33 (数値として丸める)3.33
3.333
3.33「計算結果自体を丸めたいのか」「表示だけをきれいにしたいのか」を意識して、roundか文字列フォーマットかを使い分けると良いです。
//演算子(切り捨て除算)の正しい使い方
//による整数の切り捨ての仕組み
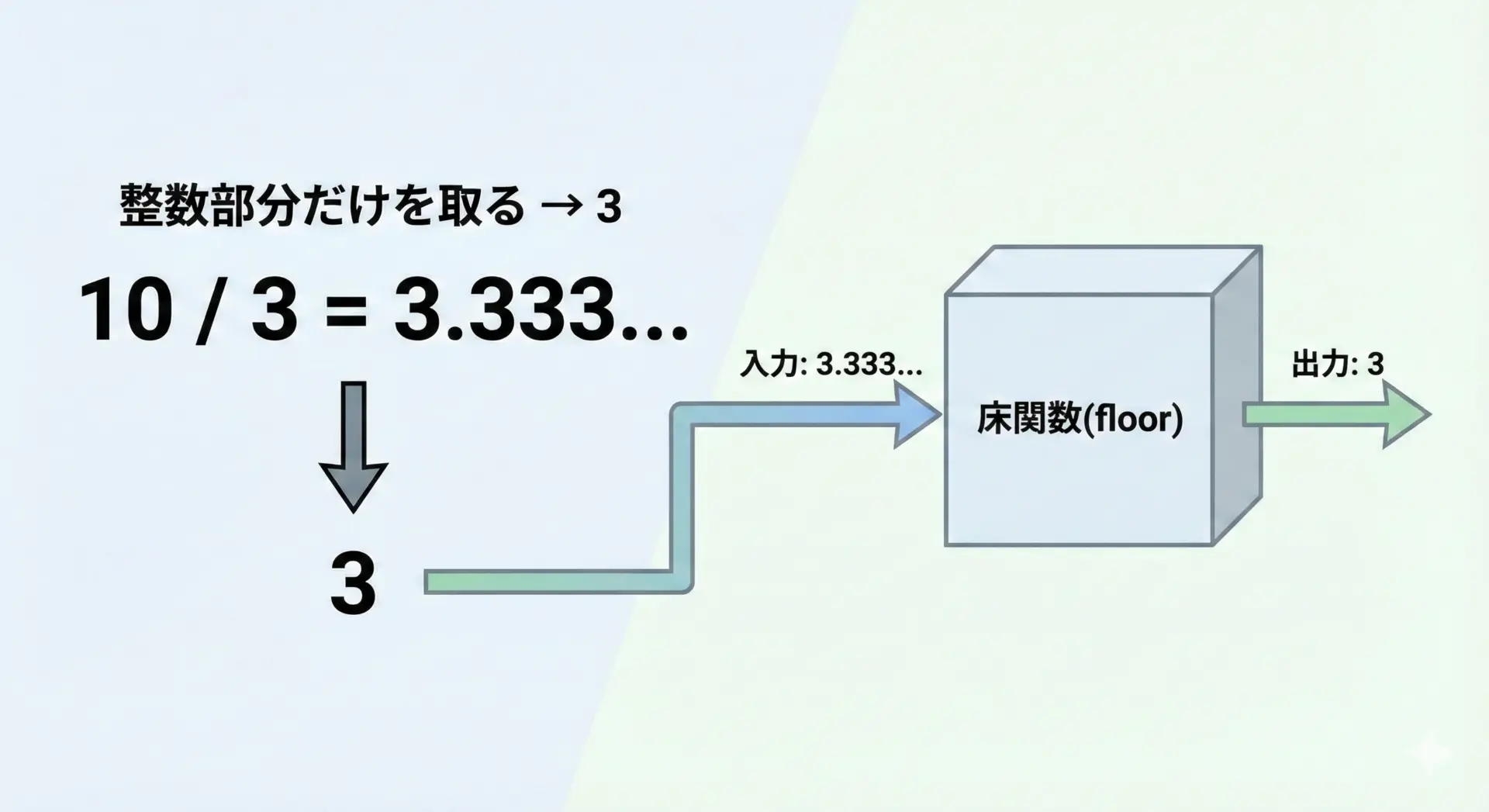
//演算子は「切り捨て除算(floor division)」です。
割り算の結果を小数点以下切り捨てた値を返します。
print(10 // 3)
print(20 // 4)
print(7 // 2)3
5
3「/ で割ってから小数点以下を切り捨てたもの」と考えると理解しやすいです。
ただし、負の数を含むときは「0方向の切り捨て」ではなく「マイナス無限大方向への切り捨て」になる点が重要です。
これは後ほど詳しく説明します。
負の数での//と数学的切り捨ての違い
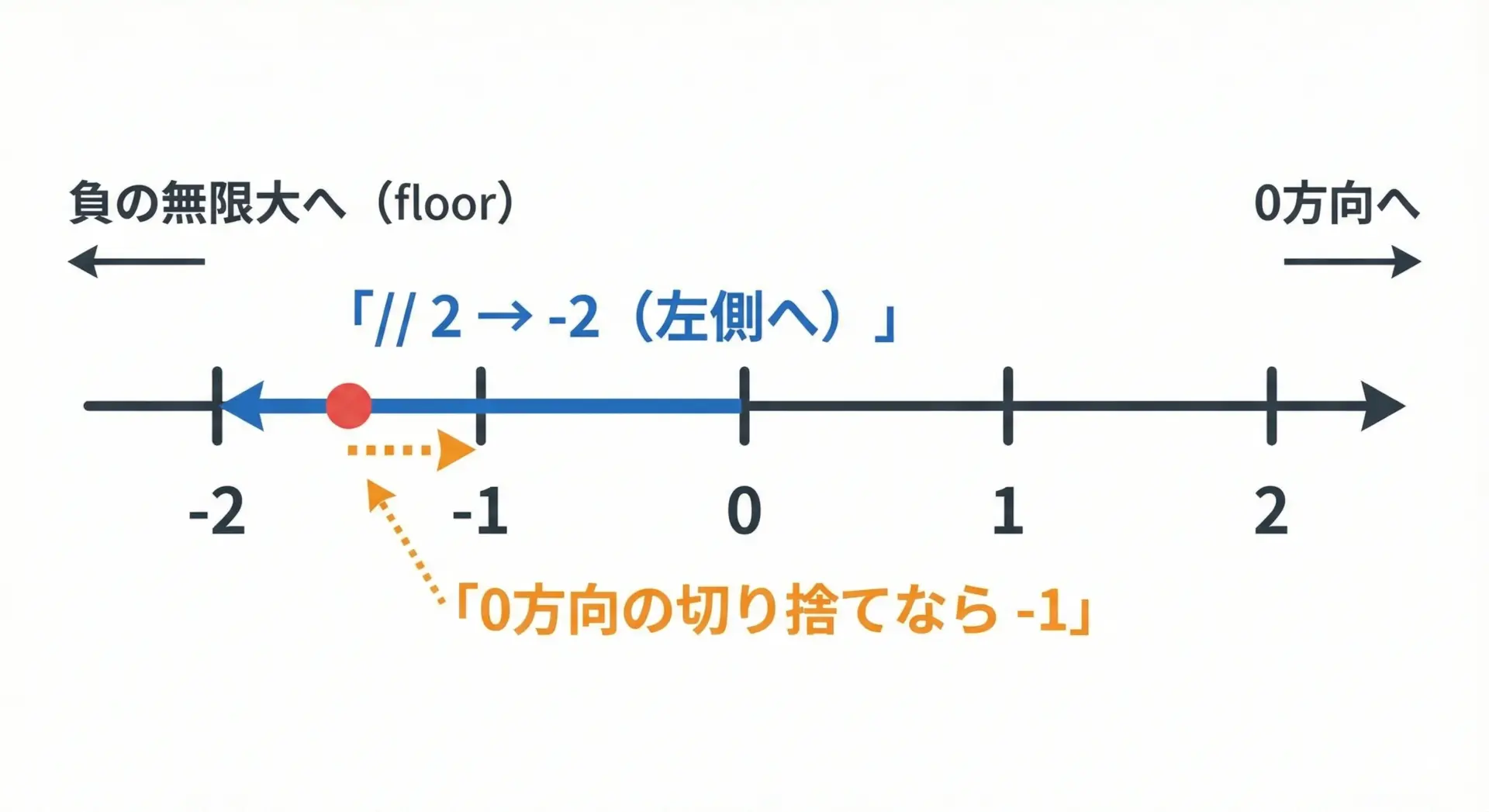
//は、「小数点以下を捨てる」のではなく「floor(床)に丸める」という挙動をします。
これは、負の数が絡むときに特に効いてきます。
print(-5 / 2) # 真の割り算
print(-5 // 2) # 切り捨て除算-2.5
-3「-2.5の小数部分を単純に削る」と考えると-2になりそうですが、Pythonの//は「-∞方向への切り捨て」なので-3になります。
他の例も確認してみます。
for a, b in [(-5, 2), (5, -2), (-5, -2)]:
print(f"{a} // {b} = {a // b}")-5 // 2 = -3
5 // -2 = -3
-5 // -2 = 20に近づけるのではなく、必ず「より小さい側」に丸めていることがわかります。
負の数で//を使う場合は、この仕様を必ず意識してください。
//とint関数、math.floorの違い
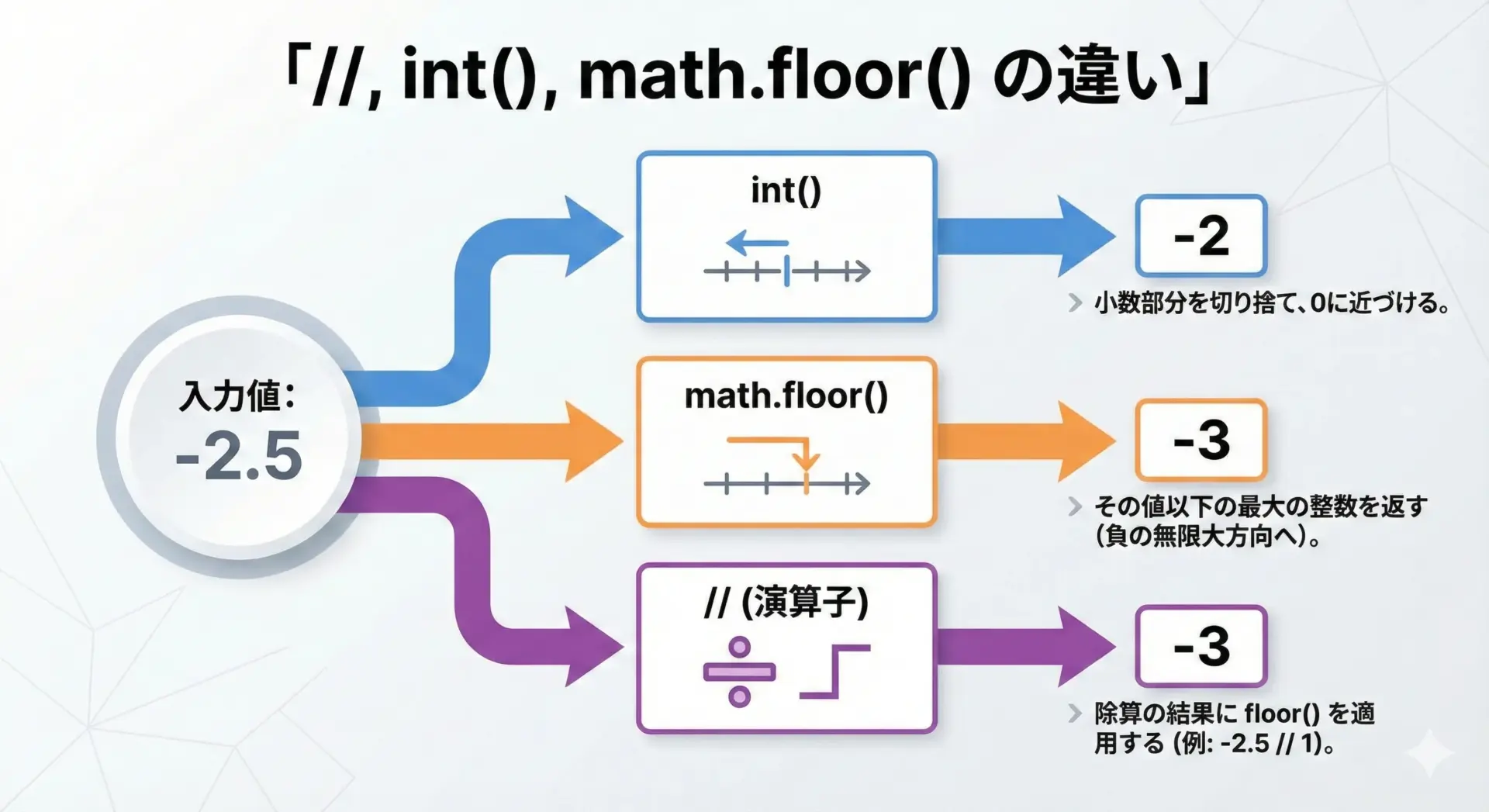
「切り捨て」と一言でいっても、Pythonにはいくつか似た機能があります。
代表的なものを比較します。
| 機能 | 対象 | -2.5 の結果 | 特徴 |
|---|---|---|---|
// 2 | 除算結果の丸め | -2 | -2.5 / 2 = -1.25 → floor(-1.25) に相当 |
int(x) | 数値→整数変換 | -2 | 0方向への丸め(小数点以下切り捨て) |
math.floor(x) | 数値→整数変換 | -3 | -∞方向への丸め |
実際にコードで見てみます。
import math
x = -2.5
print("x =", x)
print("x // 1 =", x // 1) # // は除算が前提
print("int(x) =", int(x)) # 0方向へ切り捨て
print("floor(x) =", math.floor(x)) # -∞方向へ切り捨てx = -2.5
x // 1 = -3.0
int(x) = -2
floor(x) = -3// は「割り算をしてからfloorする」もの、intは「0方向へ丸め」、math.floorは「-∞方向へ丸め」という違いがあります。
//の使いどころ
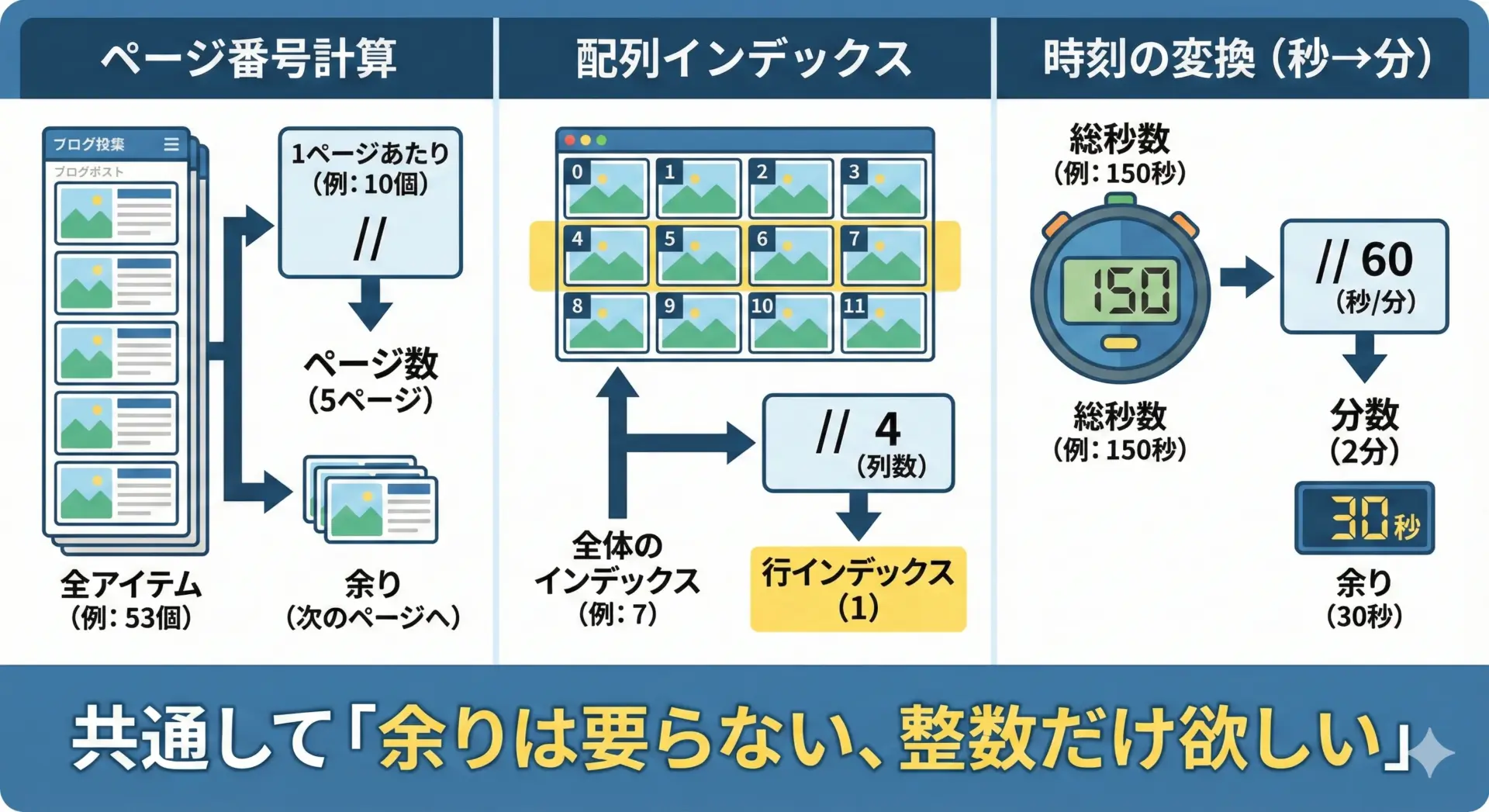
// は「余りはいらないけれど、何回分あるかだけ知りたい」ときにとても便利です。
具体的には次のような場面です。
1つ目の例として、ページネーション(ページ数の計算)を見てみます。
# 1ページに10件表示するとき、
# 全体でitems件あるときのページ数を計算する例
items = 53
per_page = 10
# 「53件を10件ずつ表示すると、何ページ必要か?」
pages = (items + per_page - 1) // per_page
print("必要なページ数:", pages)必要なページ数: 6ここでは「天井方向の丸め(切り上げ)」を行うために//をうまく利用しています。
このテクニックは、ページ数やバッチ処理の回数などを求めるときに頻繁に使われます。
他にも、時間の変換(秒→分)や配列のインデックス計算など、「割り算の結果の整数部分だけが欲しい」場面全般で//が役立ちます。
Pythonでの切り捨て・切り上げ・四捨五入の書き方
切り捨ての正しい書き方

Pythonで「切り捨て」をしたいときは、「どの方向に切り捨てたいのか」で使う関数が変わります。
代表的な書き方をコードでまとめます。
import math
x_list = [2.7, -2.7]
for x in x_list:
print(f"x = {x}")
# 0方向への切り捨て (小数点以下を単純に捨てる)
print(" int(x) =", int(x))
# -∞方向への切り捨て
print(" math.floor(x) =", math.floor(x))
# 割り算の結果を切り捨てる (//)
print(" x // 1 =", x // 1)
print()x = 2.7
int(x) = 2
math.floor(x) = 2
x // 1 = 2.0
x = -2.7
int(x) = -2
math.floor(x) = -3
x // 1 = -3.0int(x)は常に0方向へ丸めるため、-2.7 → -2になります。math.floor(x)とx // 1は-∞方向へ丸めるため、-2.7 → -3になります。
「負の値でどう動いてほしいか」を基準に、intかmath.floorか//を選ぶのが正しい使い方です。
切り上げの書き方

切り上げはmath.ceilを使います。
+∞方向へ丸めるので、正の数は大きいほうへ、負の数は0に近いほうへ動きます。
import math
x_list = [2.1, -2.1, 3.0, -3.0]
for x in x_list:
print(f"x = {x}")
print(" math.ceil(x) =", math.ceil(x))
print()x = 2.1
math.ceil(x) = 3
x = -2.1
math.ceil(x) = -2
x = 3.0
math.ceil(x) = 3
x = -3.0
math.ceil(x) = -3たとえば、「何個入りの箱に何個の商品を入れると、何箱必要か」といった場面では、切り上げがよく登場します。
そのときは次のように書けます。
import math
items = 53
per_box = 10
boxes = math.ceil(items / per_box)
print("必要な箱の数:", boxes)必要な箱の数: 6これは先ほどの//を使ったページ数計算と同じ発想です。
四捨五入の書き方(round)と注意点

四捨五入にはround関数を使いますが、Pythonのroundは学校で習う「5を常に切り上げ」とは少し違う点に注意が必要です。
Pythonのroundは「0.5は偶数側に丸める」(銀行型丸め、偶数丸め)という仕様になっています。
for x in [0.5, 1.5, 2.5, 3.5, -0.5, -1.5, -2.5]:
print(f"round({x}) = {round(x)}")round(0.5) = 0
round(1.5) = 2
round(2.5) = 2
round(3.5) = 4
round(-0.5) = 0
round(-1.5) = -2
round(-2.5) = -2このように、2.5は3ではなく2に丸められます。
「5を必ず切り上げたい」ような用途(請求金額の計算など)では、そのままroundを使うと期待と違う結果になる可能性があります。
どうしても「5を必ず切り上げ」の四捨五入をしたい場合は、自前でロジックを書くこともあります。
def round_half_up(x, ndigits=0):
"""
「0.5以上を切り上げる」形式の四捨五入を行う関数の一例です。
"""
m = 10 ** ndigits
return int(x * m + 0.5 if x >= 0 else x * m - 0.5) / m
for x in [1.5, 2.5, 3.5]:
print(x, "→ 標準round:", round(x), ", half_up:", round_half_up(x))1.5 → 標準round: 2 , half_up: 2.0
2.5 → 標準round: 2 , half_up: 3.0
3.5 → 標準round: 4 , half_up: 4.0用途に応じて「偶数丸めか」「5切り上げか」を選ぶ必要があります。
/と//を使い分けるための判断基準
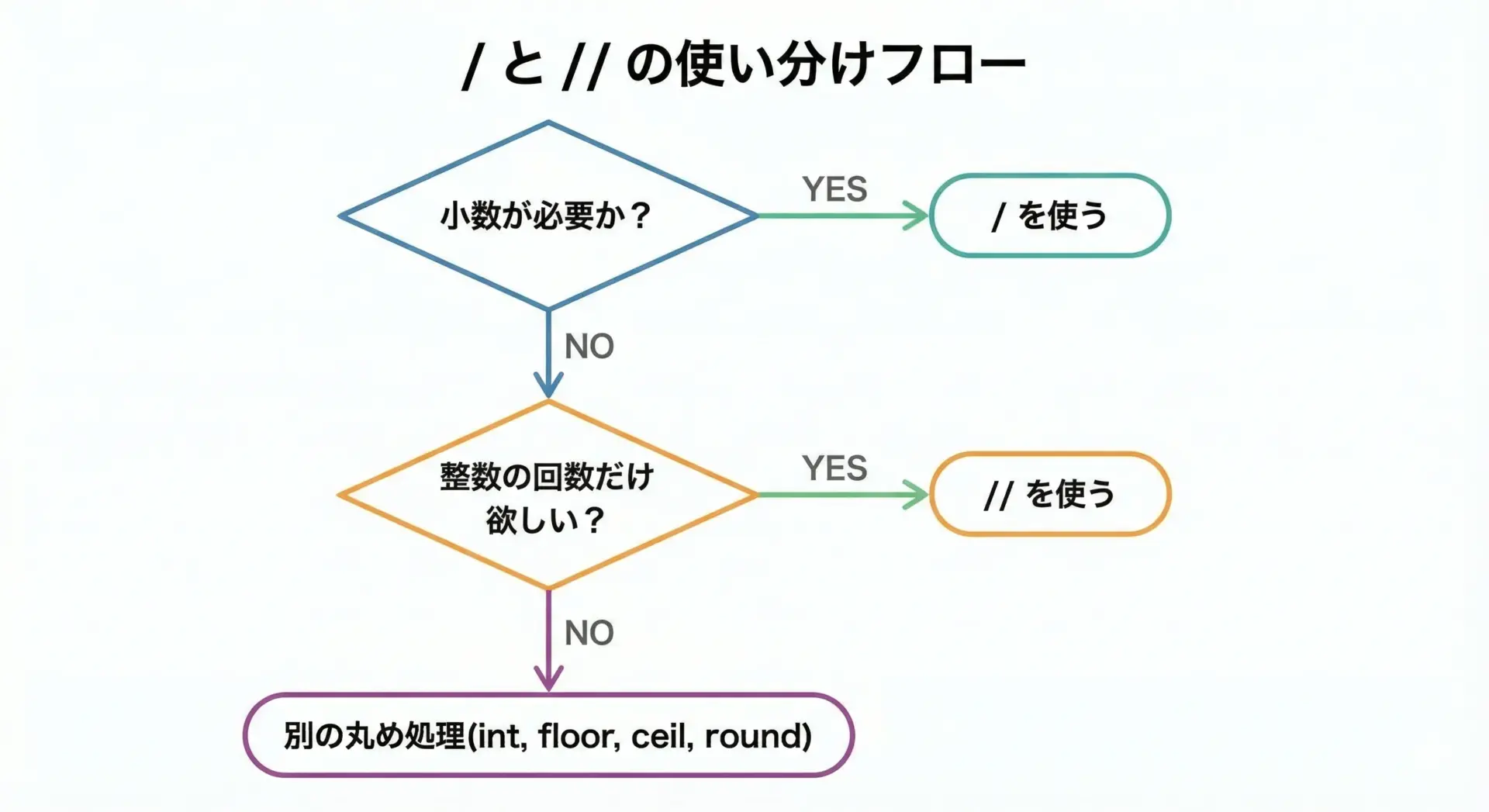
/ と // の使い分けは、「小数が欲しいのか、整数だけでよいのか」を基準に考えるとシンプルです。
おおまかな判断基準を整理します。
| 目的 | 選ぶべき演算子・関数 | コメント |
|---|---|---|
| 小数も含めて正確な計算をしたい | / | 数学通りの割り算 |
| 割り算の結果の整数部分だけ欲しい | // | 特に正の数だけ扱うなら直感的 |
| 負の数も含めて「0方向」へ切り捨てたい | int(x) | -2.7 → -2 |
| 負の数を含めて常に小さいほうへ切り捨てたい | math.floor(x) | -2.7 → -3 |
| 常に切り上げたい | math.ceil(x) | 2.1 → 3, -2.1 → -2 |
| 四捨五入(偶数丸め)したい | round(x, ndigits) | 金融系などでよく使われる方式 |
| 「.5を必ず切り上げ」したい | 独自関数(例: round_half_up) | 業務ロジックで厳密な仕様が必要な場合 |
最初に/と//の役割を正しく理解し、そのうえで必要に応じてintやmathモジュール、roundを組み合わせると、割り算まわりのバグを防ぎやすくなります。
まとめ
Pythonの/と//は見た目こそ似ていますが、「真の割り算」と「切り捨て除算」というまったく別の役割を持っています。
Python3では/は常にfloatを返し、//はfloor方向に切り捨てる点が重要です。
さらに、負の数の扱い、intやmath.floor、math.ceil、roundとの違いを理解しておくことで、切り捨て・切り上げ・四捨五入を意図通りに実装できます。
用途ごとに「どの方向に丸めたいのか」を意識しながら、/と//を正しく使い分けてください。

