「0.1 + 0.2」が「0.3」にならない問題は、多くのプログラミング初心者が一度はつまずくポイントです。
ブラウザのコンソールに0.1 + 0.2と入力すると0.30000000000000004のような結果が出て、「バグでは?」と戸惑う方も多いと思います。
本記事では、この現象の正体である浮動小数点数(IEEE 754)の仕組みを、整数との違いから実践的な対策まで、できるだけかみくだいて解説していきます。
浮動小数点数(IEEE 754)とは何か
浮動小数点数は、プログラムの中で小数を扱うための代表的な表現形式です。
ほとんどの言語でfloatやdoubleとして標準的に使われており、その多くがIEEE 754という国際標準規格に従っています。
まずは、整数との違いから「実数」をどのように近似しているのかを見ていきます。
整数との違いと「実数」の表現
整数型は、たとえば次のような値を扱います。
- …, -2, -1, 0, 1, 2, …
コンピュータ内部では、これらは2進数のビット列としてぴったり表現できます。
例えば、8ビットの符号付き整数であれば、使えるパターンは2の8乗で256通りしかなく、その範囲の整数なら誤差なく扱えます。
一方で、現実世界で扱うのは整数だけではありません。
長さ、重さ、金額、確率など、多くの量は実数(連続的な数)で表されます。
しかし、実数は「無限に細かく」取れるため、有限個のビットで完全に表すことはできません。
そこで登場するのが浮動小数点数です。
浮動小数点数は、
「限られたビット数で、広い範囲の実数をそこそこ正確に近似する」
ことを目的としています。
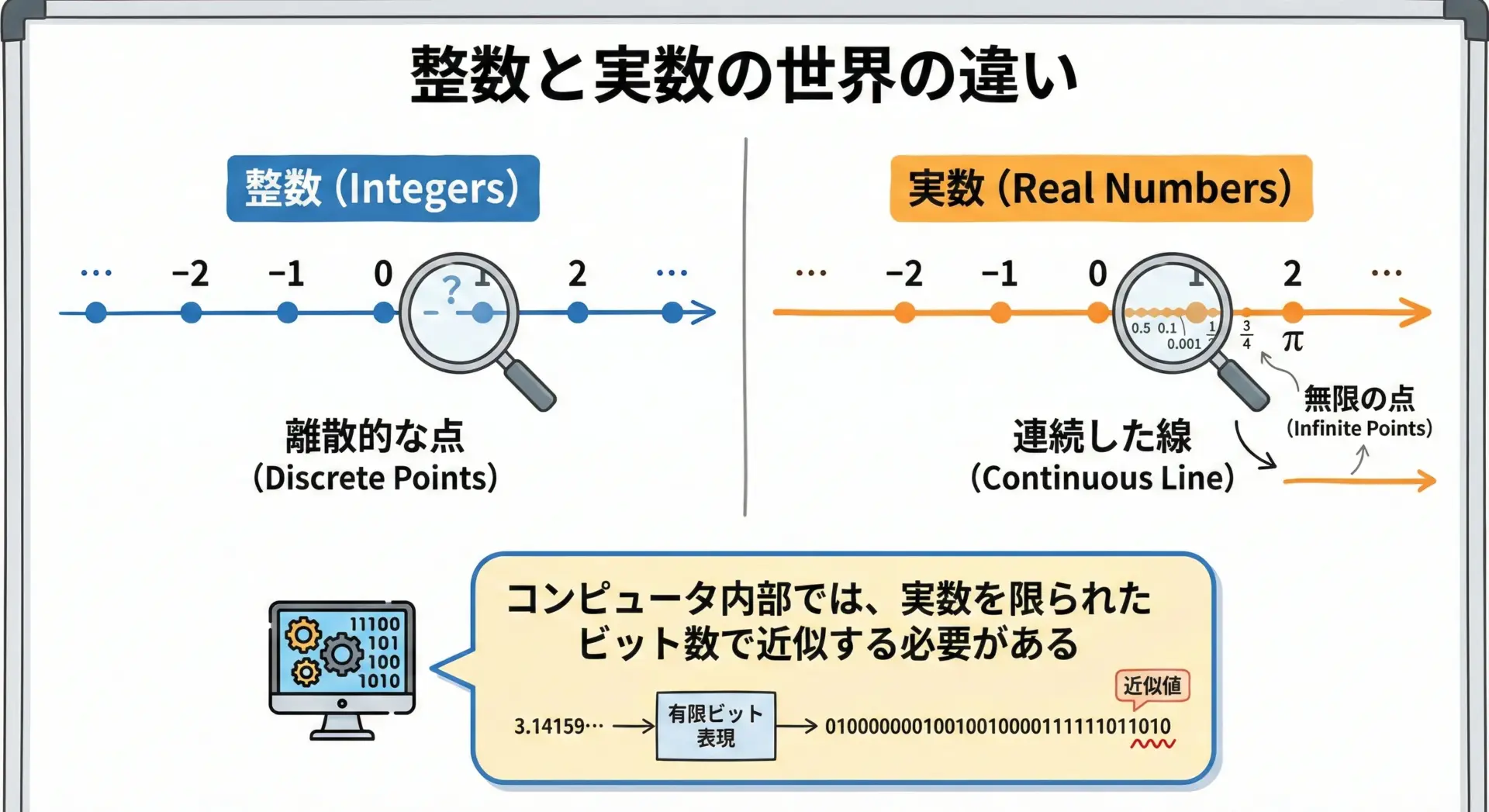
浮動小数点数では、現実の実数を「なるべく近い2進数の小数」に置き換えることで表現します。
ここに、誤差が入り込む余地があります。
IEEE 754とは
IEEE 754は、浮動小数点数の表現方法や計算ルールを定めた国際規格です。
C、C++、Java、C#、JavaScript、Pythonなど、主要なプログラミング言語の多くが、この規格に準拠した浮動小数点数を採用しています。
IEEE 754は主に次のような内容を定めています。
- 値をどのようなビット構造で表現するか
- ゼロ、無限大、NaN(Not a Number)の扱い
- 足し算・引き算・掛け算・割り算などの演算ルール
- 丸め(四捨五入など)の方法
このような共通規格があることで、異なる言語や環境でも同じ計算結果が得られやすくなっています。
浮動小数点数の基本構造
IEEE 754の代表的な形式として、次の2つがあります。
- 単精度(cst-code>float</cst-code):32ビット
- 倍精度(cst-code>double</cst-code):64ビット
ここでは倍精度(double)を例に、構造を説明します。
IEEE 754の倍精度は、次の3つの要素から構成されます。
- 符号部(sign):1ビット
- 指数部(exponent):11ビット
- 仮数部(mantissa, significand):52ビット
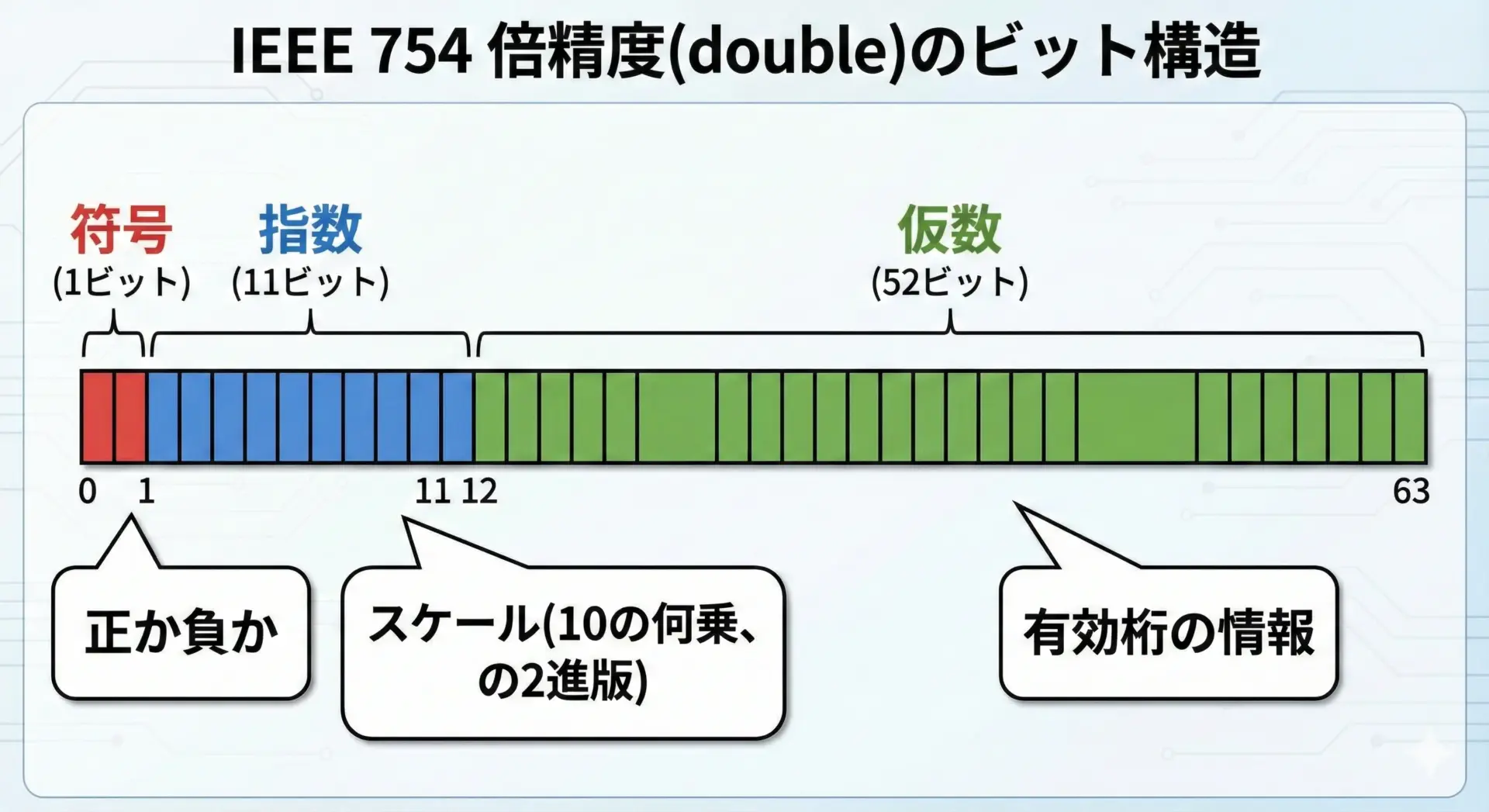
この3つを組み合わせて、値はおおまかに次のような式で表されます。
値 = 符号 × 1.xxxxxx(2進数) × 2^(指数 − バイアス)
ここで、仮数部は1.xxx…という形の小数(正規化)を2進数で表し、指数部は「2の何乗か」を表します。
整数の「固定小数点」と比べると、小数点の位置を指数で「動かす」ため、浮動小数点と呼ばれます。
0.1+0.2が0.3にならない理由
いよいよ本題です。
多くの環境で0.1 + 0.2を実行すると、0.30000000000000004など、わずかにズレた結果が返ってきます。
これは、0.1や0.2が「2進数ではぴったり表現できない」ことに由来します。
2進数では0.1も0.2も有限桁で表せない
10進数では、0.5、0.25、0.125などの値は有限桁の小数で書けます。
同様に、2進数では次のような関係があります。
- 1/2 = 0.1(2進)
- 1/4 = 0.01(2進)
- 1/8 = 0.001(2進)
つまり、分母が2のべき乗の分数は、2進数で有限桁の小数になります。
一方で、10進数の0.1(= 1/10)はどうでしょうか。
1/10は分母が2のべき乗ではないため、2進数に変換すると無限に続く小数になります。
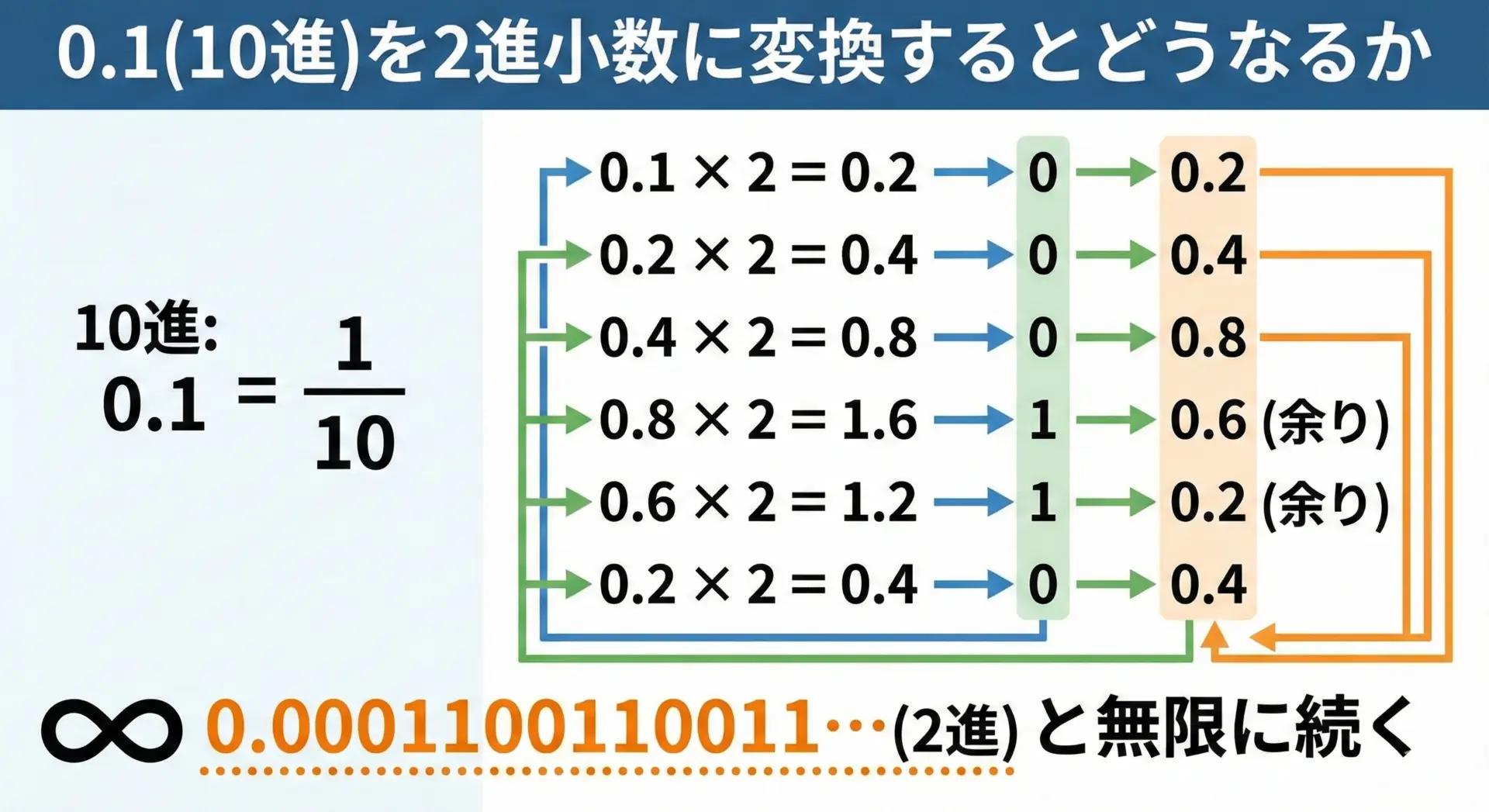
このように、10進数で有限桁の小数でも、2進数では無限に続く小数になってしまう場合があります。
0.1や0.2がまさにこれに該当します。
0.1がIEEE 754内部でどう保存されるか
実際のメモリには無限桁を保存できないため、コンピュータは途中で打ち切って最も近い値に丸めて保存します。
つまり、0.1は「本当の0.1」ではなく、「0.1に近い2進数の値」として保存されます。
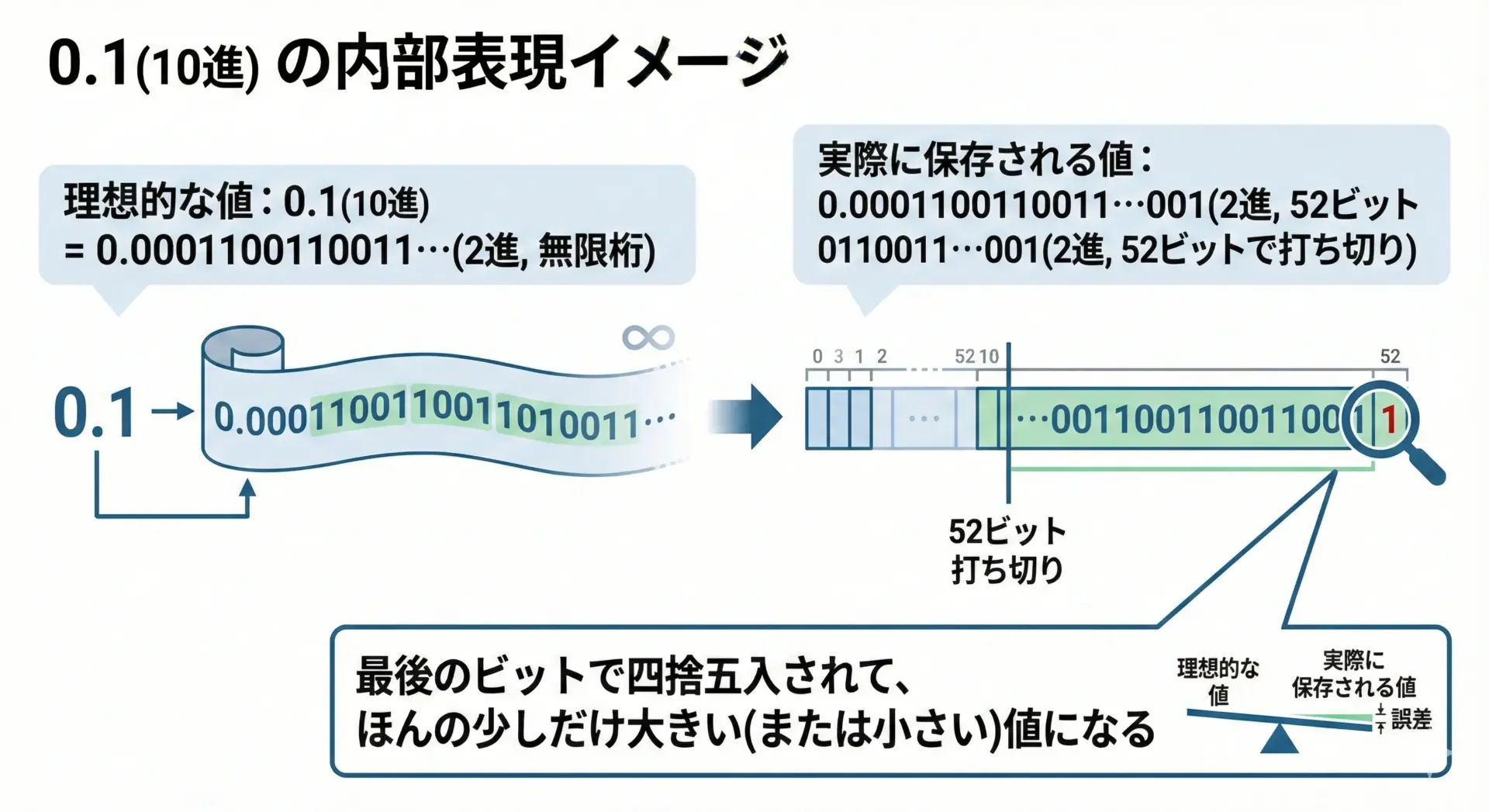
例えば、IEEE 754倍精度では、0.1は内部的におおよそ次の値として保存されます。
- 10進に直すと、およそ0.10000000000000000555…
つまり、プログラミング言語で0.1と書いても、内部的には「0.1っぽいけど完全ではない値」が使われていることになります。
同様に、0.2も「0.2に限りなく近いが、厳密には違う値」として保存されます。
丸め誤差がたまって0.3000000004…になる仕組み
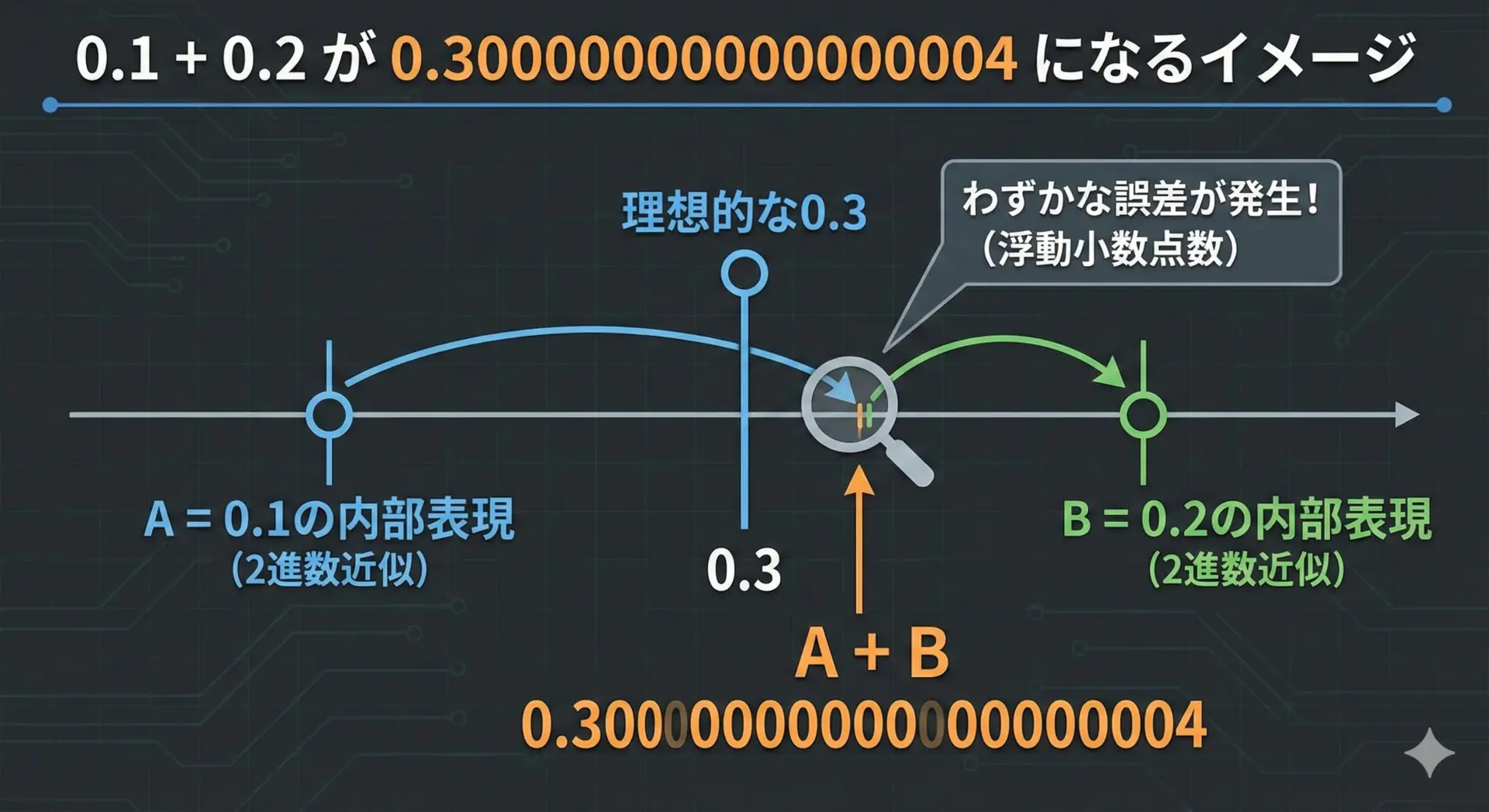
ここまでを踏まえて、0.1 + 0.2を式として分解してみます。
- 内部的には、
- 0.1 ≒ A (Aは0.1に近いが、わずかにずれた値)
- 0.2 ≒ B (Bも同様)
- したがって、
- 0.1 + 0.2 ≒ A + B
このAとBはどちらも「ほんの少しだけ本来の値と違う」ので、足したときの誤差もまた少し大きくなります。
その結果として、0.3からわずかにズレた値になり、それを10進数で表示すると0.30000000000000004のような見慣れない結果になります。
プログラミング言語によっては、小数の表示桁数を制限したり、見た目を丸めたりしているため、常に誤差が見えるとは限りません。
しかし、内部的には多くの小数が「近似値」であることは変わりません。
なぜ「== 0.3」で比較するとfalseになるのか
ここで、次のようなコードを考えてみます。
0.1 + 0.2 == 0.3内部的には、
- 左辺: 「0.3に非常に近いが、完全には等しくない値」
- 右辺: 0.3に最も近い2進の近似値
になっています。
左辺と右辺は、どちらも「0.3っぽい値」ですが、ビットレベルでは異なるため、多くの言語ではfalseになります。
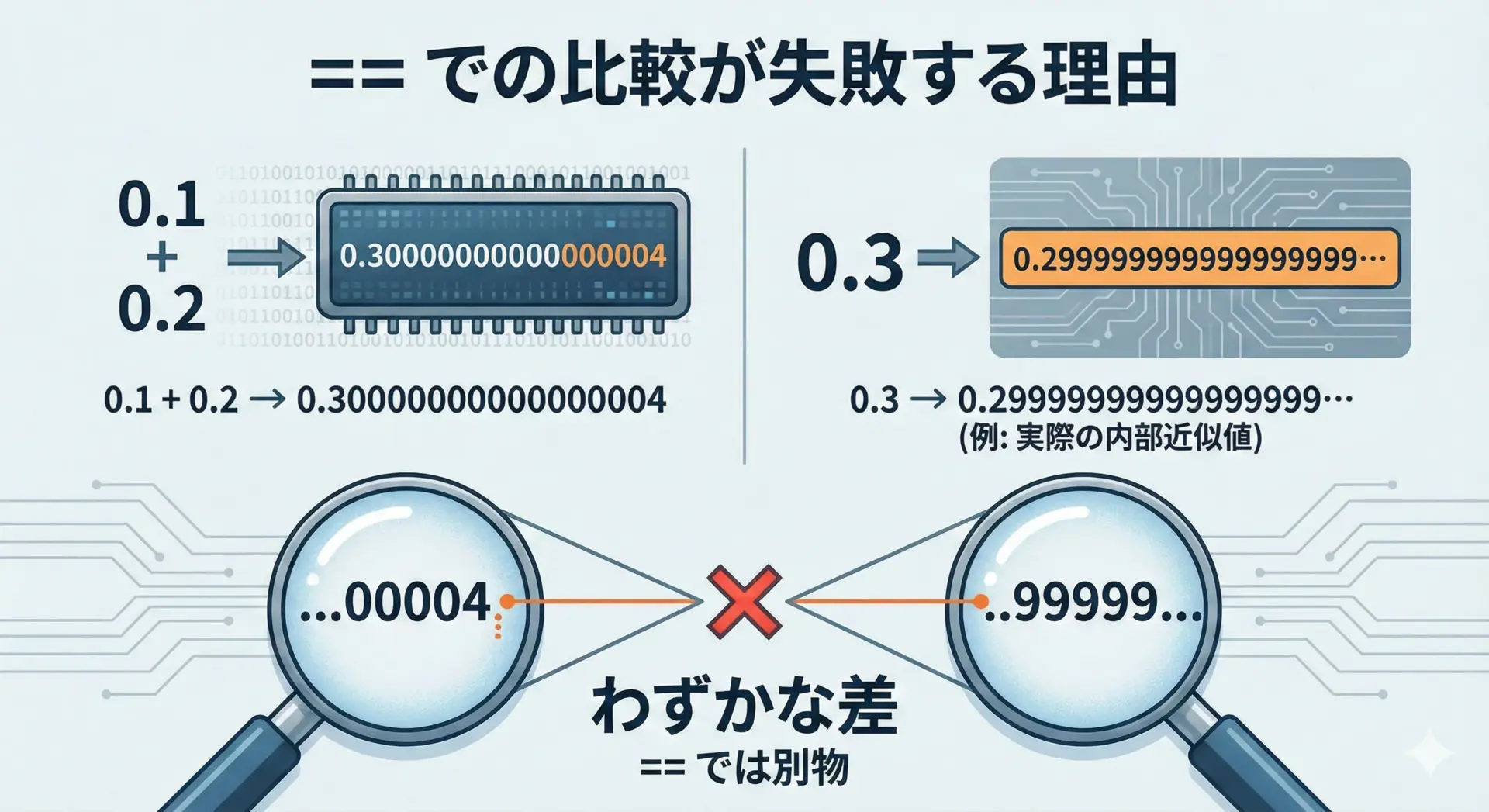
このように、浮動小数点数を「完全一致」で比較するのは危険です。
次のセクションでは、こうした誤差の種類と注意点を整理します。
浮動小数点数の誤差の種類と注意点
浮動小数点数には、いくつか典型的な誤差のパターンがあります。
誤差の正体と、どういう場面で問題になりやすいかを押さえておくことで、バグを未然に防ぎやすくなります。
丸め誤差と桁落ちとは
丸め誤差とは、有限のビット数に収めるために四捨五入した結果として生じる誤差です。
先ほどの0.1の例のように、「理論値」と「内部で保持される値」の差そのものが丸め誤差です。
一方、桁落ちは、ほぼ同じ大きさの数値同士を引き算したときに有効桁が失われる現象です。
たとえば、
- 0 と 0.0001 を足したり引いたりする
- 非常に近い値同士を差分として扱う
といった計算を繰り返すと、下位の桁がどんどん失われていき、相対的な誤差が大きくなります。

どちらも「ビット数(有効桁数)が有限である」ことから生じる問題です。
代表的なハマりどころ
浮動小数点数の誤差は、次のような場面で実際のバグとして表面化しやすいです。
- ループ回数の条件に小数を使う
- 例:
for (x = 0.0; x != 1.0; x += 0.1)のようなコードが無限ループになる
- 例:
- UIやログに表示される値が「0.3」ではなく「0.30000000000000004」となり、ユーザーが困惑する
- 金額やポイントの計算で1円(1ポイント)単位のズレが発生し、トラブルにつながる
- 比較演算(
==,<,>)の結果が直感と異なる
「少数第N位まで正確なはず」と思い込んでしまうと、これらの問題に気づきにくくなります。
単精度(float)と倍精度(double)の違い
単精度(cst-code>float)と倍精度(cst-code>double)の主な違いは、使えるビット数(=有効桁数)と表現できる範囲です。
次のように整理できます。
| 型 | ビット数 | 有効桁(おおよそ10進) | 主な用途のイメージ |
|---|---|---|---|
| float | 32ビット | 約7桁 | 画像処理、3D計算など |
| double | 64ビット | 約15〜16桁 | 一般的な数値計算、金融以外 |
doubleはfloatよりも誤差が小さく、広い範囲を表現できますが、それでも「完全に誤差ゼロ」ではありません。
0.1や0.2を完全に表現できないという本質は、どちらでも同じです。
誤差とうまく付き合うための実践テクニック
誤差を完全にゼロにすることはできませんが、誤差が問題にならないように「設計」でコントロールすることはできます。
ここでは、代表的な対策をいくつか紹介します。
誤差を前提にした比較方法
浮動小数点数を比較するときは、「完全一致(==)」ではなく「ある許容範囲内かどうか」を基準にするのが定石です。
たとえば、
a = 0.1 + 0.2
b = 0.3
eps = 1e-9 # 許容誤差(イプシロン)
abs(a - b) < eps # True なら「ほぼ等しい」とみなすここでのポイントは以下の通りです。
- 絶対値で差を取り、その差が十分小さいかどうかを判定する
- eps(イプシロン)の値は用途に応じて決める
- 金額なら「0.0000001未満なら同じ」といった業務要件ベースで決める
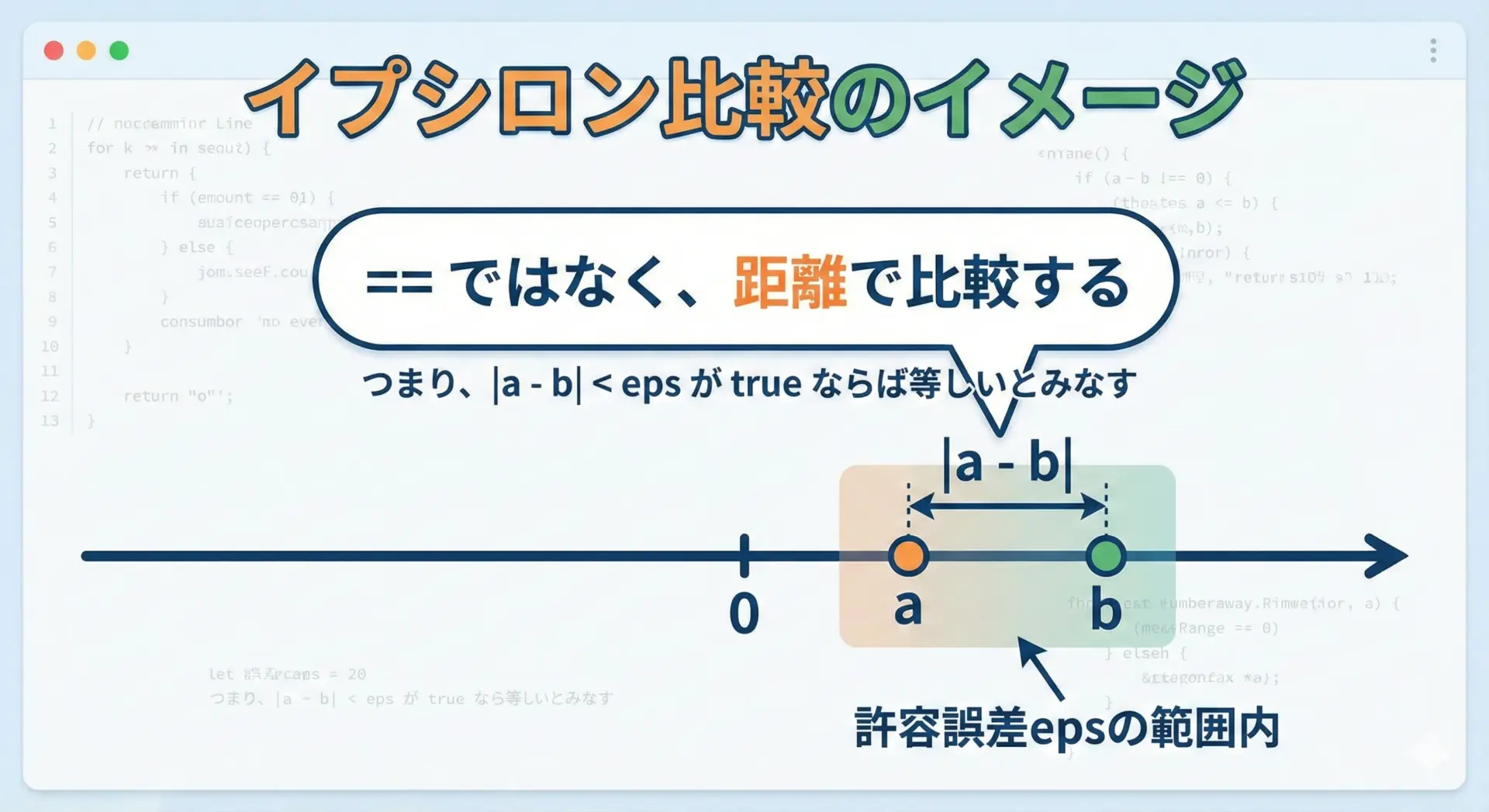
多くの数値計算ライブラリやテストフレームワークも、同様の「イプシロン比較」を内部で行っています。
金額やポイント計算での対策
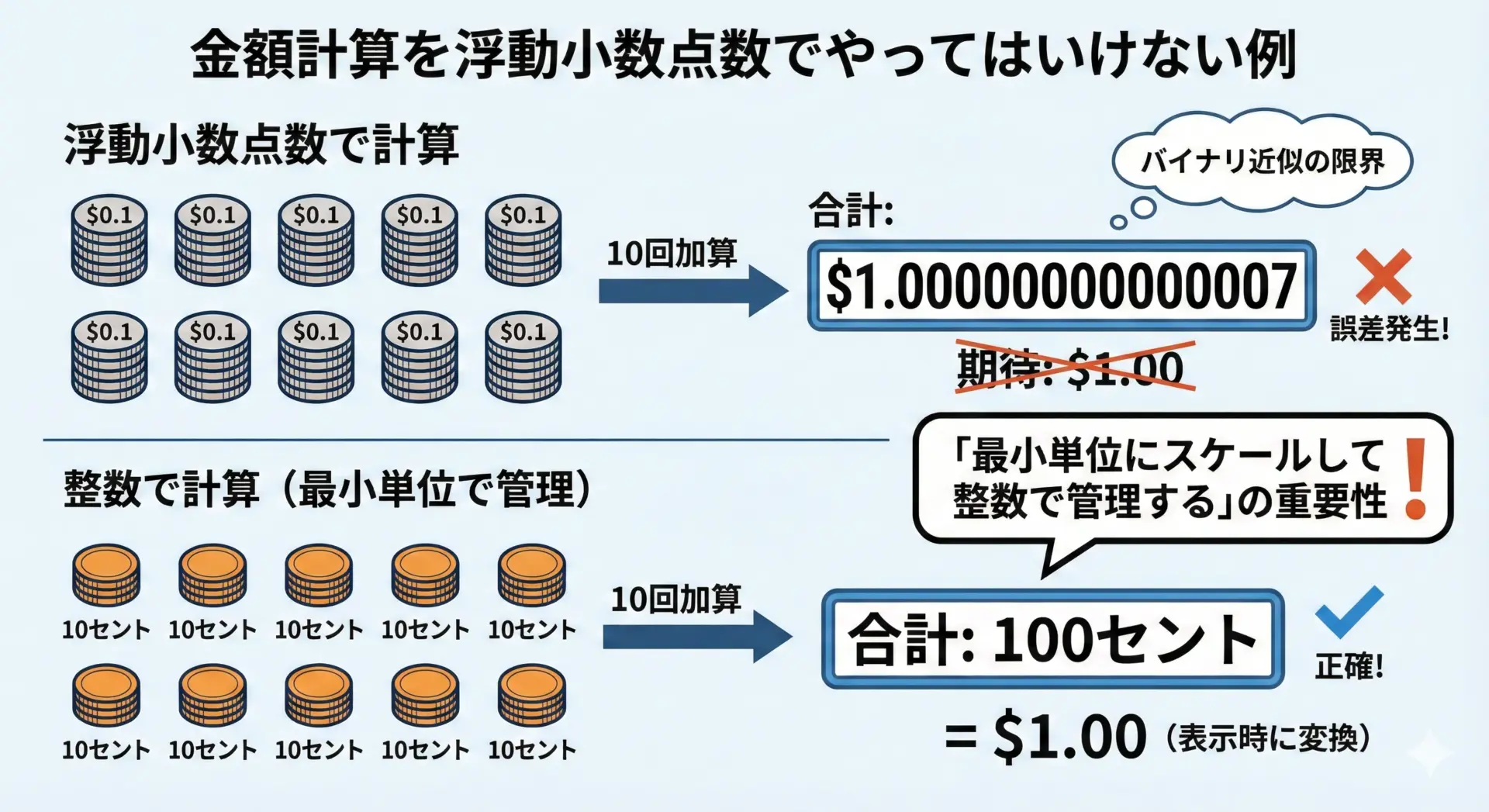
金額、ポイント、在庫数など、「1単位」でもズレてはいけない分野では、浮動小数点数をそのまま使うのは危険です。
よく使われる対策としては次のようなものがあります。
- 整数で管理する
- 金額を「円」ではなく「銭」や「センチ」など、最小単位まで整数化して扱う
- 例: 1,234円56銭 → 123456(整数)として保持する
- 利点: 整数なら丸め誤差が発生しない
- 丸めルールを明示しておく
- 計算の途中や最終結果を必ず小数第2位で四捨五入するなど、仕様上のルールを決めて実装に落とし込む
- 言語の標準ライブラリや金融向けライブラリの丸め機能を積極的に利用する
ライブラリやdecimal型を使う選択肢
多くの言語には、10進小数を厳密に扱うための型やライブラリが用意されています。
代表的なものとして次のような型が挙げられます。
- Java:
BigDecimal - C#:
decimal - Python:
decimal.Decimal - JavaScript: 外部ライブラリ(
decimal.jsなど)
これらは、おおむね次のような特徴を持ちます。
- 基本的に10進表現を前提としており、「0.1」を正確に表現できる
- 加減乗除の結果も10進的に厳密
- その代わり、計算コストやメモリ消費が増える
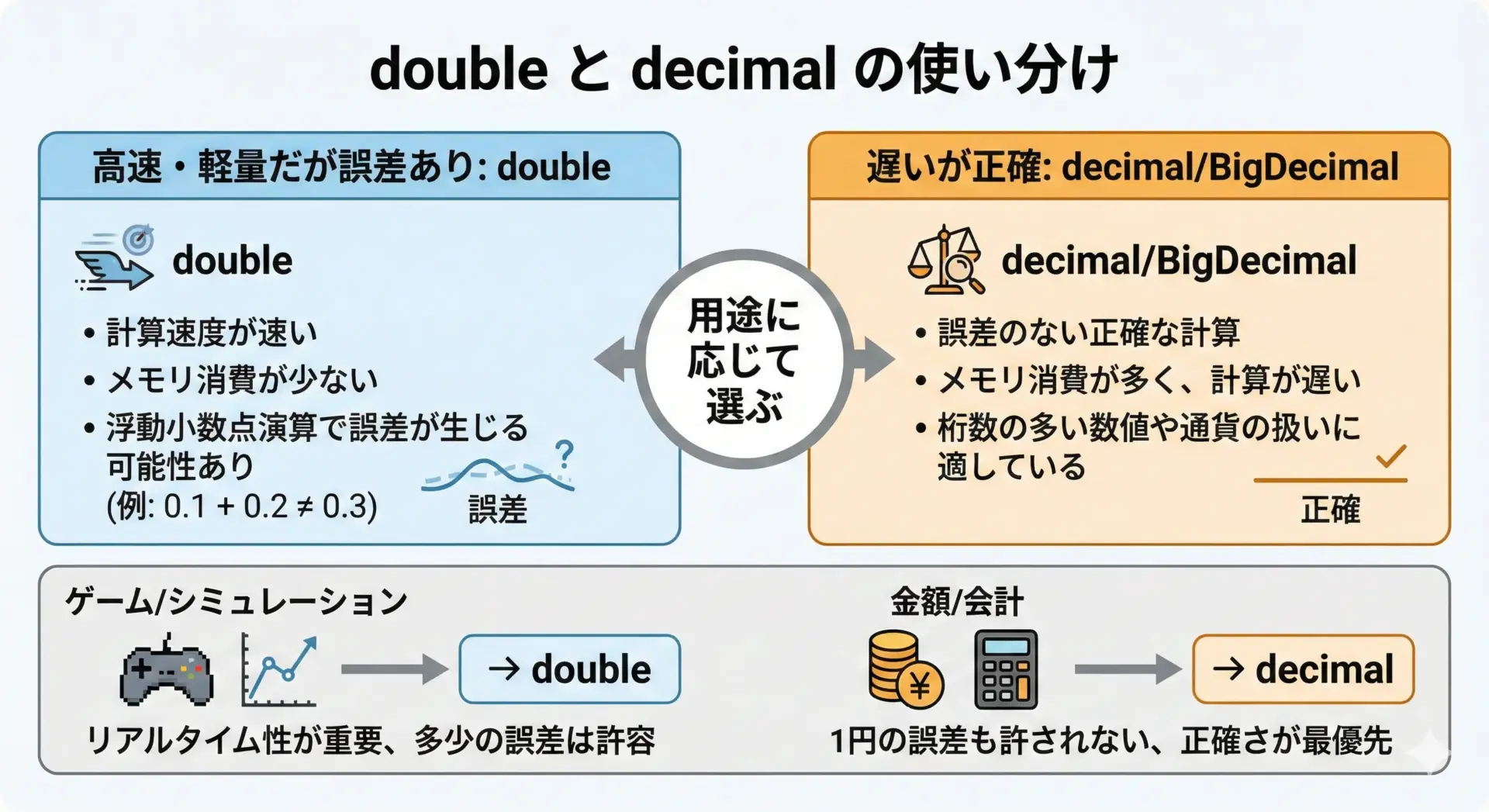
金融・会計などの分野では、これらのdecimal系の型がほぼ必須と言ってよいでしょう。
目的に合わせた数値型の選び方
最後に、実務で考えやすい数値型の選び方の指針をまとめます。
- 個数・ID・カウントなど「割り切れた整数」
→整数型(int, longなど)
誤差は絶対に許されないので、浮動小数点数は避けます。 - 物理シミュレーション、3Dグラフィックス、統計など「多少の誤差が許容される測定量」
→double(倍精度)
広い範囲と速度が重要で、多少の丸め誤差は前提とします。 - 厳密な金額・税計算、請求書・明細など「1単位のズレも許されない値」
→decimal/BigDecimal または「最小単位で整数管理」
パフォーマンスより正確さを優先します。 - 組み込み・GPU計算など、メモリや速度が極端に重要な場面
→float(単精度)
ただし誤差が増えることを前提にアルゴリズムを設計します。
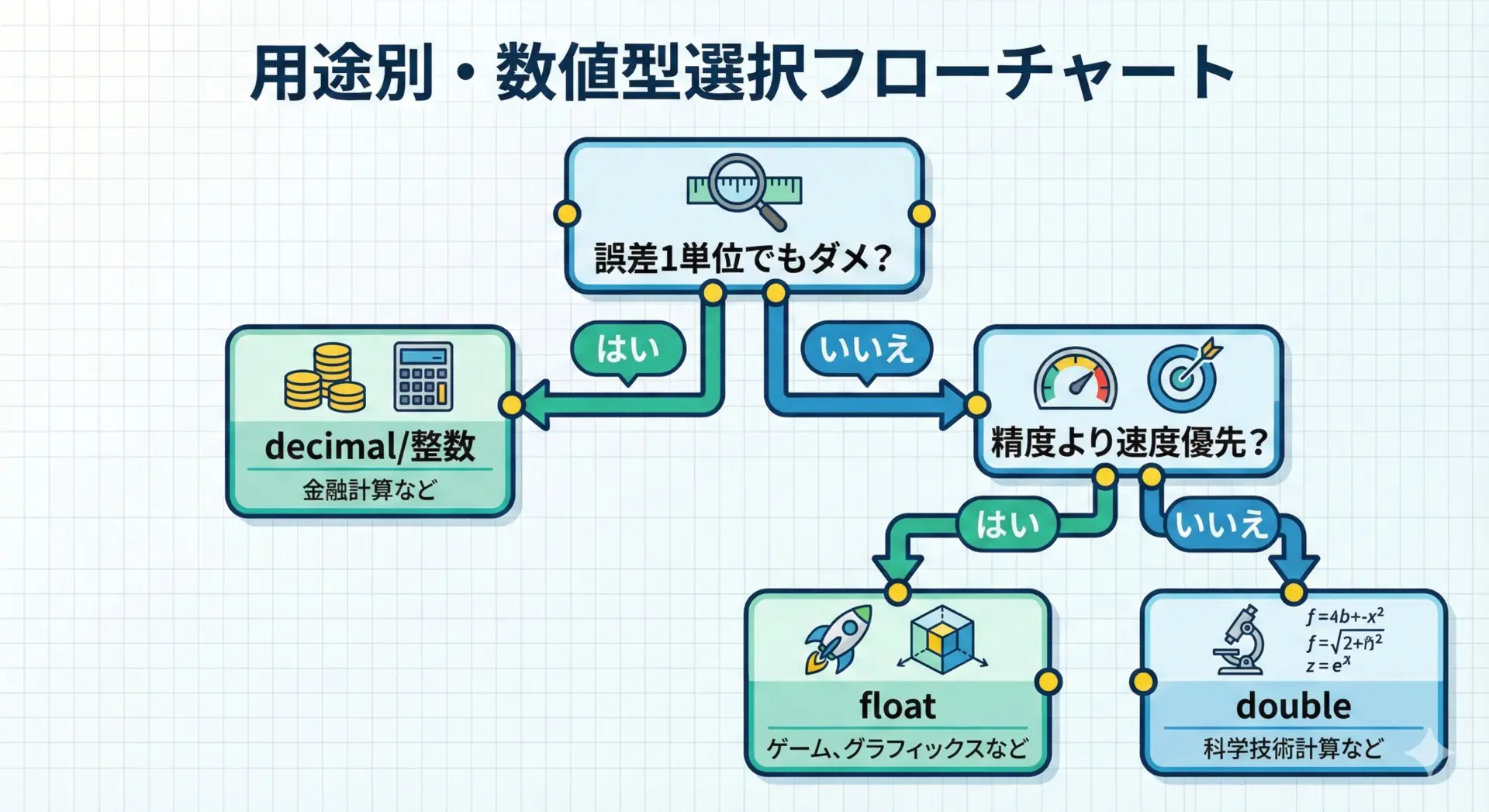
「何をどれくらい正確に扱いたいのか」を先に決め、それに合った型や戦略を選ぶことが重要です。
まとめ
本記事では、「0.1 + 0.2 が 0.3 にならない」理由から出発して、浮動小数点数(IEEE 754)の仕組みと付き合い方を解説しました。
- 浮動小数点数は、有限のビット数で実数を近似するための仕組みであり、その国際標準がIEEE 754です。
- 1や0.2は、2進数では無限に続く小数になるため、内部では丸められた近似値として保存されます。
- その結果、0.1 + 0.2 はビットレベルでは 0.3 と一致せず、
== 0.3という比較がfalseになることがあります。 - 浮動小数点数の誤差には、丸め誤差や桁落ちなどがあり、ループ条件や金額計算などでバグの原因になりやすいです。
- 実務では、イプシロン比較を用いたり、金額は整数やdecimal型で扱うなど、誤差を前提にした設計が不可欠です。
- double、float、decimal(あるいは整数)など、用途に応じて最適な数値型を選ぶことが、信頼性の高いプログラムにつながります。
「浮動小数点数は信用できない」と避けてしまうのではなく、どの程度まで信用できて、どこから先は工夫が必要なのかを理解することが重要です。
今回紹介した考え方やテクニックを押さえておけば、「0.1 + 0.2 問題」にもう悩まされることはないはずです。

