【C言語】 expとlogの使い方【eのx乗・自然対数・エラー対策まで】

2025年10月25日2025年12月9日

C言語

指数関数expと対数関数logは、C言語で数値計算を行ううえで避けて通れない重要な関数です。

特に、機械学習や統計処理、物理シミュレーションでは必ずといってよいほど登場します。

本記事では、C言語のexp・logの基本から、オーバーフロー対策やエラー処理まで、実務でそのまま使える形で丁寧に解説します。

目次 [ close ]

expとlogとは

expとlogの基本

expとlogは、いわゆる指数関数と対数関数を表す数学関数です。

高校数学で学ぶ内容と対応していますが、C言語では型やエラー処理など、プログラミングならではの注意点が加わります。

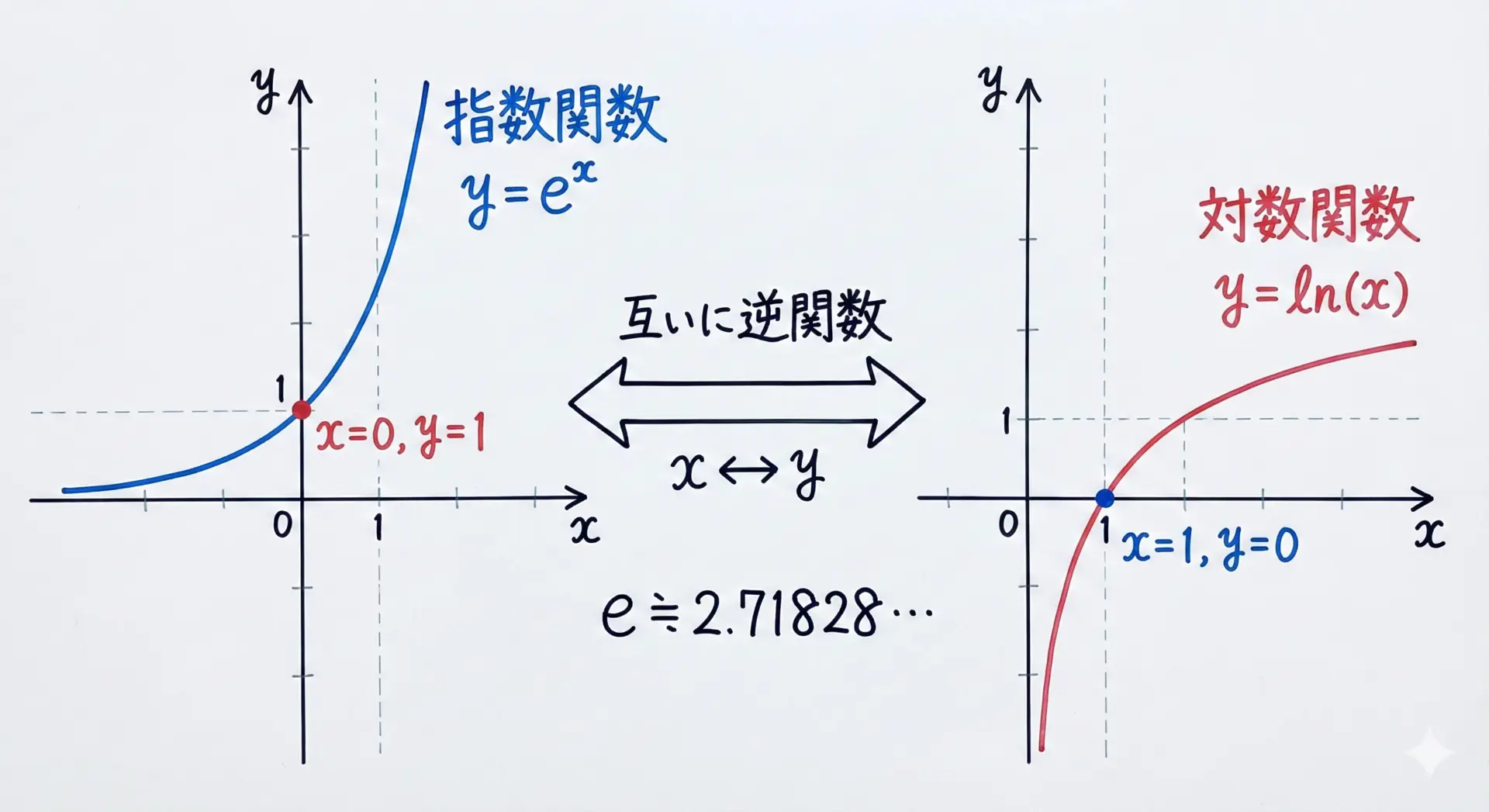
指数関数exp(x)は、数学でいうe^xを表します。

ここでeは自然対数の底であり、約2.71828…という無限小数です。

指数関数は、複利計算、成長・減衰モデル、確率分布の表現などで多用されます。

一方、対数関数log(x)は、数学でいうln(x)(自然対数)に対応し、e^y = xとなるyを返します。

指数関数の逆関数であり、掛け算・べき乗を足し算に変換するという性質から、計算上とても扱いやすい関数です。

math.hで使うC言語のexpとlog関数一覧

C言語では、math.hをインクルードすると、浮動小数点の型に応じたexp・log系の関数を利用できます。

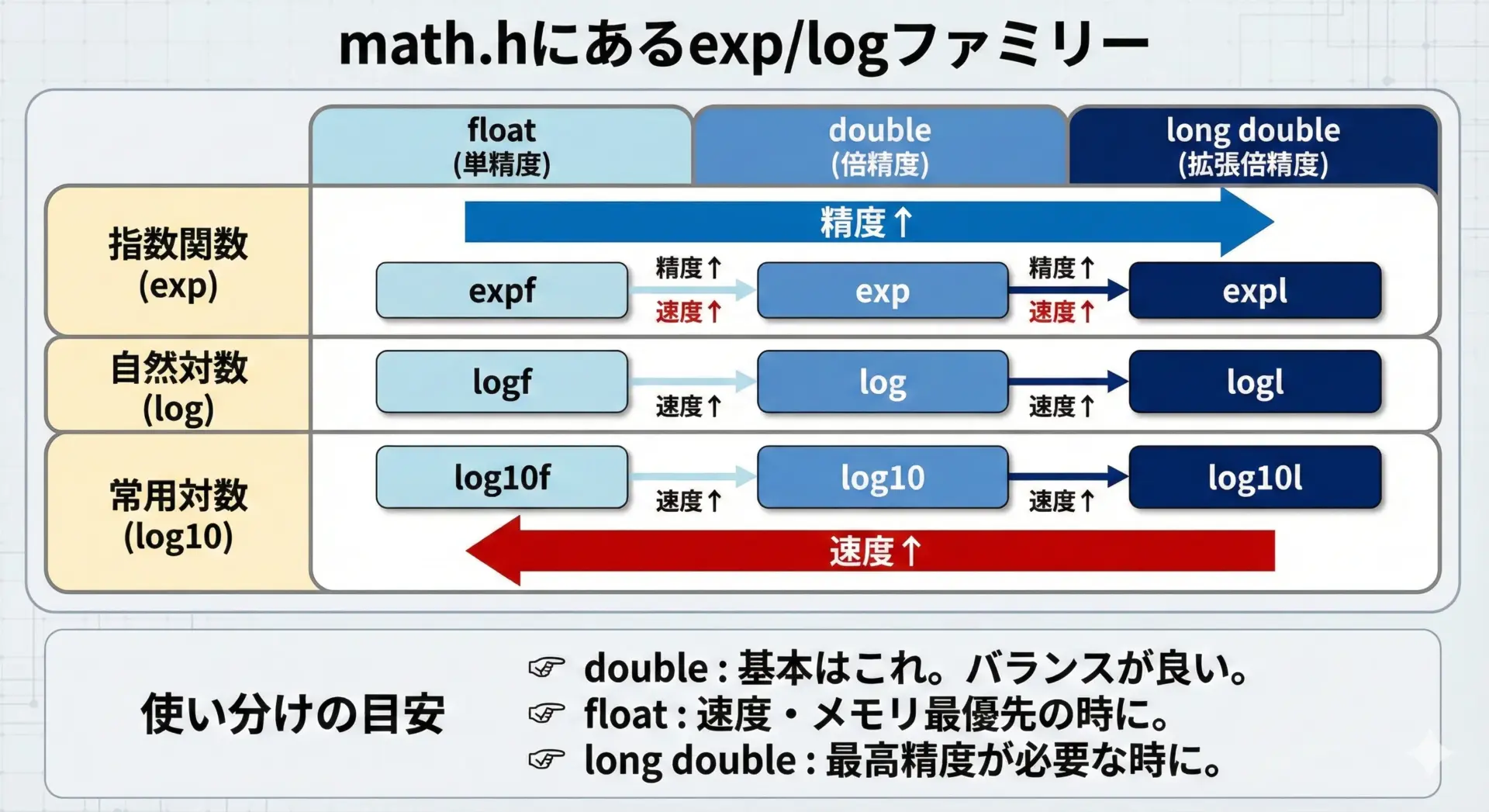
代表的な関数を、型ごとに整理すると次のようになります。

種類	double版	float版	long double版	意味
指数(自然底)	`exp`	`expf`	`expl`	eのx乗(cst-code>e^x)
自然対数	`log`	`logf`	`logl`	ln(x)
常用対数(底10)	`log10`	`log10f`	`log10l`	log10(x)
任意底対数(実装例)	ー	ー	ー	`log(x)/log(b)` で計算

double精度の関数(引数・戻り値ともにdouble)が標準的な選択肢です。

性能やメモリを重視する場合にfloat版、より高精度が必要な場合にlong double版を検討します。

expとlogがC言語で使われる代表的な場面

exp・logは、次のような実装でよく使われます。

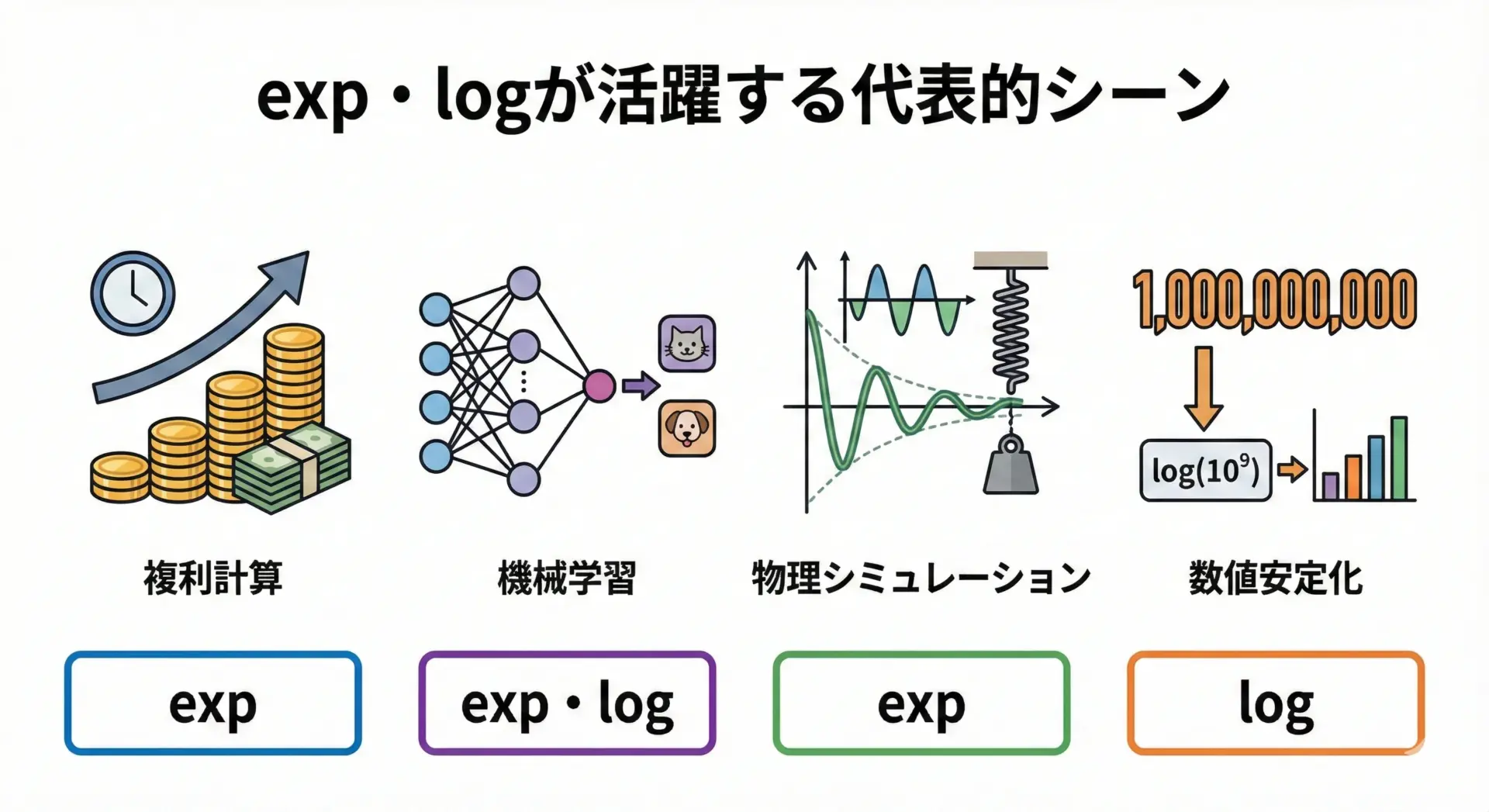
たとえば、利子や人口増加、放射性物質の減衰のような指数的な成長・減衰のモデルではexpが登場します。

また、ガウス分布(正規分布)の計算、ソフトマックス関数、ロジスティック回帰などの確率・統計・機械学習でもexpは頻出です。

一方でlogは、べき乗計算の変形、オーダーの大きく異なる値の集計(ログスケールでの足し算)、エントロピー計算などで多く使われます。

非常に大きい値や非常に小さい値を、そのまま扱うとオーバーフロー・アンダーフローを起こす場面で、logを取って安全に計算するというテクニックもよく使われます。

exp関数の使い方

exp関数の書式と戻り値

C言語で最も基本となるexp関数は、次のように宣言されています。

C言語

#include <math.h>

double exp(double x);

戻り値はdouble型で、e^x(自然底eのx乗)を返します。

有効な引数としては、負の値も含めた任意の実数が利用できます。

極端に大きな正の値を渡した場合にはオーバーフローしてHUGE_VALなどの無限大が返り、極端に小さな負の値ではアンダーフローでゼロに近い値が返されることがあります。

float型・long double型のexpfとexpl

浮動小数点型に応じて、float版・long double版の関数も用意されています。

C言語

#include <math.h>

float       expf(float x);          // float版の指数関数
long double expl(long double x);    // long double版の指数関数

通常の数値計算ではexp(double)を使うのがバランスがよいですが、次のようなケースで使い分けを検討します。

メモリサイズや処理速度を優先する組込み用途: expf
高精度な科学技術計算や多倍長演算との連携: expl

ただし、型を混在させると暗黙の型変換が発生して意図しない精度低下を招くことがあるため、変数の型と関数のバージョンをそろえることが重要です。

expの使用例

簡単な使用例として、いくつかの値に対してexpを計算してみます。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double x1 = 0.0;
    double x2 = 1.0;
    double x3 = -1.0;

    // exp(x) = e^x を計算
    printf("exp(%.1f) = %.10f\n", x1, exp(x1));  // e^0 = 1
    printf("exp(%.1f) = %.10f\n", x2, exp(x2));  // e^1 ≒ 2.71828...
    printf("exp(%.1f) = %.10f\n", x3, exp(x3));  // e^-1 ≒ 0.36788...

    return 0;
}

実行結果

exp(0.0) = 1.0000000000
exp(1.0) = 2.7182818285
exp(-1.0) = 0.3678794412

このように、0を渡すと1、正の値で急速に増加し、負の値では0に近づきます。

expでよくある桁あふれ(オーバーフロー)の注意点

expは、引数が大きいほど結果が指数的に増大します。

そのため、ある閾値を超えるとオーバーフローを起こしてしまいます。

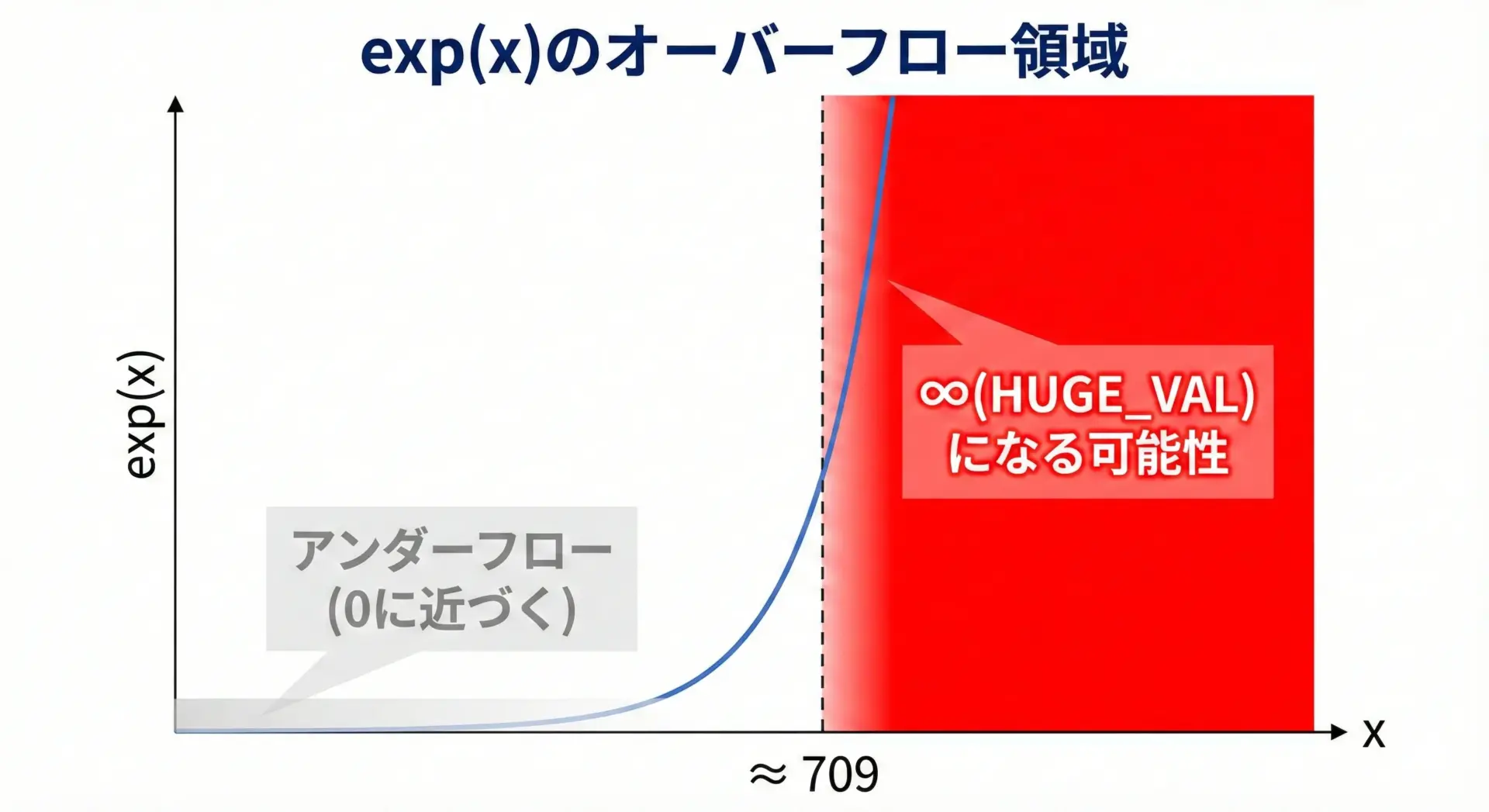
double精度では、おおよそx ≈ 709を超えたあたりからexp(x)がオーバーフローして無限大となります。

実際には実装依存ですが、概ねこの付近が限界です。

オーバーフローが起こると、次のような挙動になります。

返り値: HUGE_VALなど(正の無限大)
errno: ERANGEがセットされる可能性がある
場合によっては浮動小数点例外が発生

このような症状を避けるには、事前に引数の範囲をチェックして安全な範囲内にクリップ(制限)する、あるいは後述するlogスケールでの計算への置き換えを検討します。

expを使った指数計算のコツと実装パターン

expは、単にe^xを計算するだけでなく、べき乗一般に応用できます。

たとえば、a^bは次の恒等式で書き換えられます。

a^b = exp(b * log(a))

これを用いると、powが使えない場面でもべき乗を実装できます。

C言語

#include <stdio.h>
#include <math.h>

// a^b を exp と log を使って計算する例
double my_pow(double a, double b) {
    // a > 0 が必要 (log(a) の定義域のため)
    if (a <= 0.0) {
        // 簡単のため、異常値は0を返す
        // 実務ではエラーコードやNaNを返すなど適切な扱いが必要です
        return 0.0;
    }
    return exp(b * log(a));
}

int main(void) {
    double a = 2.0;
    double b = 3.0;
    printf("my_pow(%.1f, %.1f) = %.10f\n", a, b, my_pow(a, b));  // 2^3 = 8
    return 0;
}

実行結果

my_pow(2.0, 3.0) = 8.0000000000

また、数値安定性の観点から「大きな値同士の割り算」を「log差のexp」に変換するといったテクニックもよく利用されます。

例えば、2つの確率pとqについてp/qを求める際、両方とも非常に小さい場合には次のように計算することでアンダーフローを避けられます。

p/q = exp(log(p) - log(q))

log関数の使い方

log関数の書式と戻り値

C言語のlogは、自然対数(底e)を計算する関数です。

C言語

#include <math.h>

double log(double x);

戻り値はdoubleで、数学的なln(x)に対応します。

定義域はx > 0のみであり、0や負の値を渡すと未定義動作やNaNが返る可能性があります。

この点はexpと大きく異なります。

float型logf・long double型loglの違い

expと同様に、logにも型ごとのバリエーションがあります。

C言語

#include <math.h>

float       logf(float x);          // float版の自然対数
long double logl(long double x);    // long double版の自然対数

一般的なPCアプリケーションやサーバーサイドプログラムではdouble版のlogを使うのが標準です。

組込みのようにメモリ・CPU資源に厳しい環境ではlogf、数値解析やシミュレーションで高精度が要求される場合にloglを検討します。

log10関数で常用対数(10の対数)を求める

自然対数だけでなく、底10の対数(常用対数)を求めたい場面もあります。

その場合にはlog10関数を用います。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double x1 = 10.0;
    double x2 = 1000.0;

    printf("log10(%.0f) = %.2f\n", x1, log10(x1));   // 10^1 → 1
    printf("log10(%.0f) = %.2f\n", x2, log10(x2));   // 10^3 → 3

    return 0;
}

実行結果

log10(10) = 1.00
log10(1000) = 3.00

なお、log10(x)はlog(x)/log(10.0)と等価ですが、専用関数を使う方が一般に精度・速度の両面で有利です。

logで負の値・ゼロを渡したときの挙動

logは、数学的にはx > 0でのみ定義されます。

そのため、C言語でも負の値やゼロを渡すと問題が発生します。

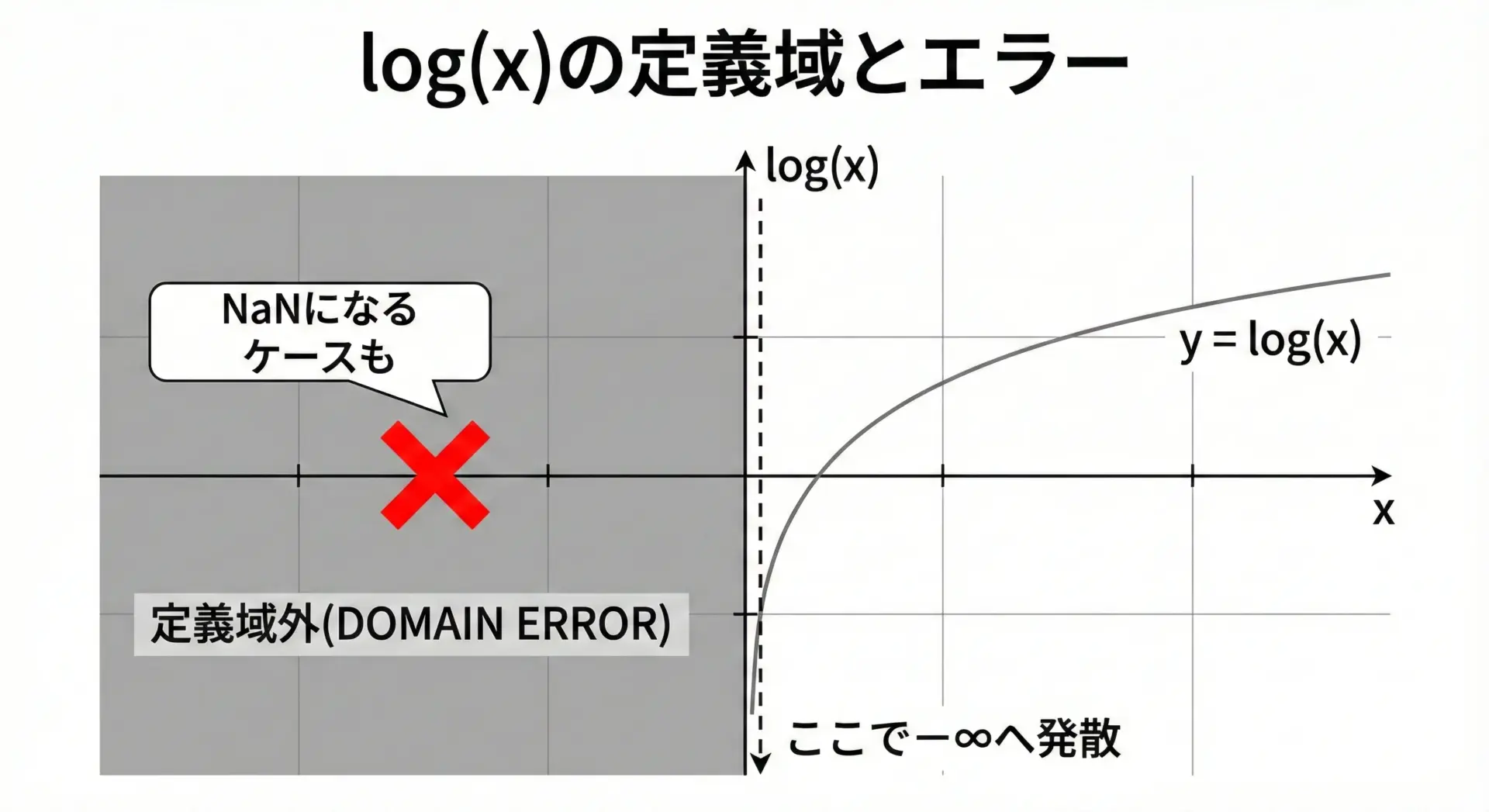
代表的な挙動は次の通りです。

log(0.0): 負の無限大(-HUGE_VAL)や-inf相当、errnoにERANGEがセットされる場合もあります。
log(負の値): NaN(非数)になり、errnoにEDOMなどのドメインエラーが設定される実装もあります。

実務では、logを呼び出す前にx > 0かどうかを必ずチェックすることが重要です。

C言語

#include <stdio.h>
#include <math.h>

// x > 0 のときにだけ log(x) を計算する安全なラッパー例
double safe_log(double x) {
    if (x <= 0.0) {
        // 本来はエラーコードやNaNを返すなど要件に応じて設計します
        printf("safe_log: invalid argument x = %f\n", x);
        return NAN;    // NaN を返してエラーを示す
    }
    return log(x);
}

int main(void) {
    printf("safe_log(10.0) = %f\n", safe_log(10.0));
    printf("safe_log(0.0)  = %f\n", safe_log(0.0));   // エラー扱い
    printf("safe_log(-1.0) = %f\n", safe_log(-1.0));  // エラー扱い
    return 0;
}

実行結果

safe_log(10.0) = 2.302585
safe_log: invalid argument x = 0.000000
safe_log(0.0)  = nan
safe_log: invalid argument x = -1.000000
safe_log(-1.0) = nan

logを使った指数方程式の解き方と実装例

logは、指数方程式を解くのに非常に有効です。

例えば、次のような方程式を考えます。

a * e^(b x) = c

この方程式をxについて解くには、両辺のlogを取ります。

a * e^(b x) = c
両辺をaで割る: e^(b x) = c / a
両辺の自然対数を取る: b x = log(c / a)
x = log(c / a) / b

これをCで計算してみます。

C言語

#include <stdio.h>
#include <math.h>

// a * e^(b x) = c を x について解く関数
// 前提: a != 0, c/a > 0, b != 0
double solve_exp_equation(double a, double b, double c) {
    double ratio = c / a;
    if (ratio <= 0.0 || b == 0.0) {
        // 条件を満たさない場合は NaN を返す
        return NAN;
    }
    return log(ratio) / b;
}

int main(void) {
    double a = 2.0;
    double b = 0.5;
    double c = 10.0;

    double x = solve_exp_equation(a, b, c);
    printf("Solution x = %f\n", x);

    // 検算: left = a * exp(b * x)
    double left = a * exp(b * x);
    printf("Check: a * exp(b * x) = %f (should be %f)\n", left, c);

    return 0;
}

実行結果

Solution x = 3.218876
Check: a * exp(b * x) = 10.000000 (should be 10.000000)

このように、指数方程式をlogで線形な形に変形し、最後に必要ならexpで戻すという流れは、数値計算で非常によく使われます。

powとlog・expを組み合わせたべき乗計算

前述のように、a^bはexp(b * log(a))で表せます。

C言語には標準でpow関数がありますが、数値安定性や性能のためにあえてlog・expで自前実装することもあります。

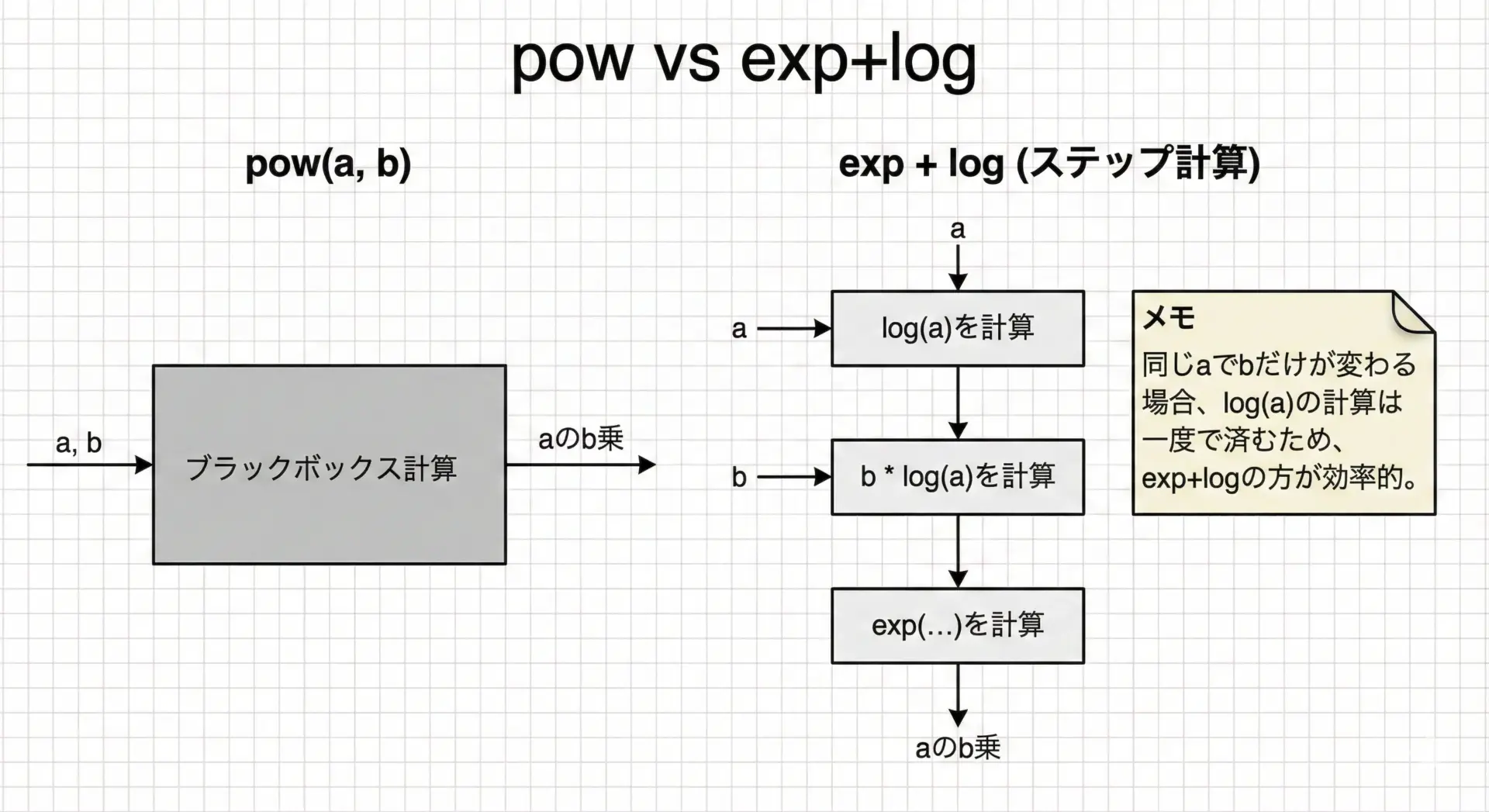
例えば、同じaに対して、異なるbを何度も計算する場合には、log(a)を一度だけ計算しておき、あとはexpだけを繰り返し呼び出すと効率がよくなります。

C言語

#include <stdio.h>
#include <math.h>

// 同じ a に対して複数の指数 b[i] で a^b[i] を計算する例
void compute_powers(double a, const double *exponents, int n, double *results) {
    if (a <= 0.0) {
        // log(a) が定義されないので、本来はエラー処理を行うべき
        for (int i = 0; i < n; ++i) {
            results[i] = NAN;
        }
        return;
    }

    double log_a = log(a);  // 1回だけ計算

    for (int i = 0; i < n; ++i) {
        double b = exponents[i];
        results[i] = exp(b * log_a);  // a^b = exp(b * log(a))
    }
}

int main(void) {
    double a = 2.0;
    double exps[] = {1.0, 2.0, 3.0, 10.0};
    double results[4];

    compute_powers(a, exps, 4, results);

    for (int i = 0; i < 4; ++i) {
        printf("2^%.0f = %f\n", exps[i], results[i]);
    }

    return 0;
}

実行結果

2^1 = 2.000000
2^2 = 4.000000
2^3 = 8.000000
2^10 = 1024.000000

このような「一度logを取っておいて、expで何度も復元する」パターンは、性能チューニングでも有効です。

exp・logのエラー対策と実装上の注意

ここからは、exp・logを安全に使うための実務的なエラー対策について解説します。

errnoとmathエラー(DOMAIN・RANGE)の扱い方

exp・logなどの数学関数は、errnoを通じてエラーを知らせることがあります。

代表的なエラーは次の2種類です。

種類	意味	典型的な例
DOMAINエラー	定義域外の引数	`log(-1.0)` など
RANGEエラー	範囲外の結果(オーバーフロー・アンダーフロー)	`exp(1000.0)` など

実際のエラー検出には、errnoを0にリセットしてから関数を呼び、戻り値とerrnoの組み合わせを見る方法がよく使われます。

C言語

#define _USE_MATH_DEFINES
#include <stdio.h>
#include <math.h>
#include <errno.h>   // errno, EDOM, ERANGE

int main(void) {
    errno = 0;
    double y1 = log(-1.0);   // DOMAIN error の可能性

    if (errno == EDOM) {
        printf("log(-1.0): DOMAIN error (EDOM)\n");
    } else if (errno == ERANGE) {
        printf("log(-1.0): RANGE error (ERANGE)\n");
    }
    printf("log(-1.0) = %f\n", y1);

    errno = 0;
    double y2 = exp(1000.0); // RANGE error の可能性

    if (errno == EDOM) {
        printf("exp(1000.0): DOMAIN error (EDOM)\n");
    } else if (errno == ERANGE) {
        printf("exp(1000.0): RANGE error (ERANGE)\n");
    }
    printf("exp(1000.0) = %f\n", y2);

    return 0;
}

実行結果

log(-1.0): DOMAIN error (EDOM)
log(-1.0) = -nan
exp(1000.0): RANGE error (ERANGE)
exp(1000.0) = inf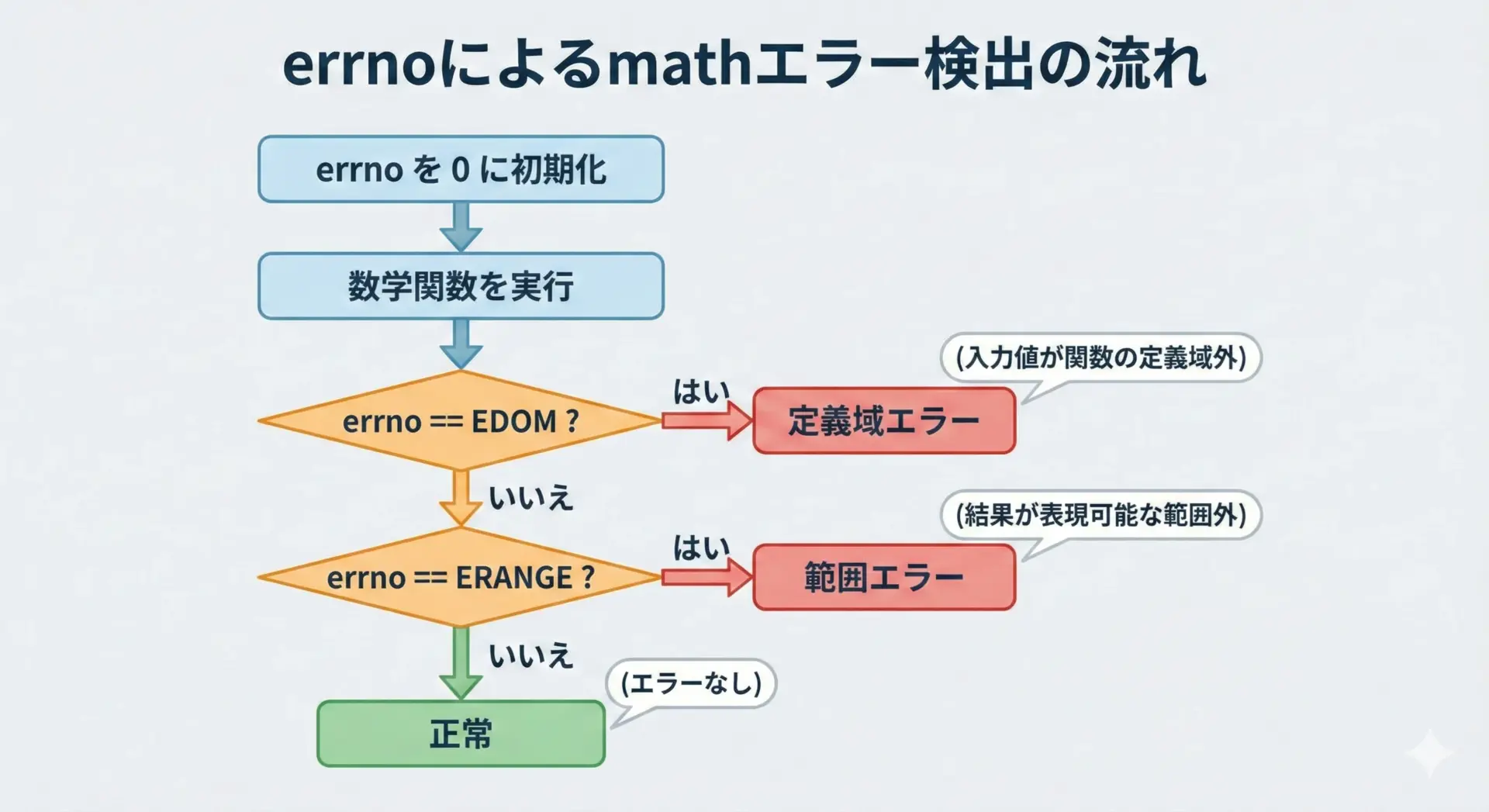

ただし、errnoが必ず設定されるかどうか、またどの値になるかは処理系依存の部分もあり得ます。

重要なロジックでは、後述するisnan・isfiniteなどと組み合わせて、より堅牢なチェックを行うべきです。

isnan・isfiniteでNaNや無限大を検出する方法

exp・logの計算結果がNaN(Not a Number)や無限大になることがあります。

これらを検出するには、math.hで定義される次のマクロや関数を使います。

isnan(x): xがNaNなら非0を返す
isfinite(x): xが有限の数なら非0を返す
isinf(x): xが±∞なら非0を返す

C言語

#include <stdio.h>
#include <math.h>

void print_status(const char *name, double x) {
    printf("%s = %f: ", name, x);

    if (isnan(x)) {
        printf("NaN\n");
    } else if (isinf(x)) {
        printf("Infinity\n");
    } else if (isfinite(x)) {
        printf("Finite\n");
    } else {
        printf("Unknown\n");
    }
}

int main(void) {
    double a = log(-1.0);    // NaN の可能性
    double b = exp(1000.0);  // Infinity の可能性
    double c = log(10.0);    // 有限

    print_status("log(-1.0)", a);
    print_status("exp(1000.0)", b);
    print_status("log(10.0)", c);

    return 0;
}

実行結果

log(-1.0) = -nan: NaN
exp(1000.0) = inf: Infinity
log(10.0) = 2.302585: Finite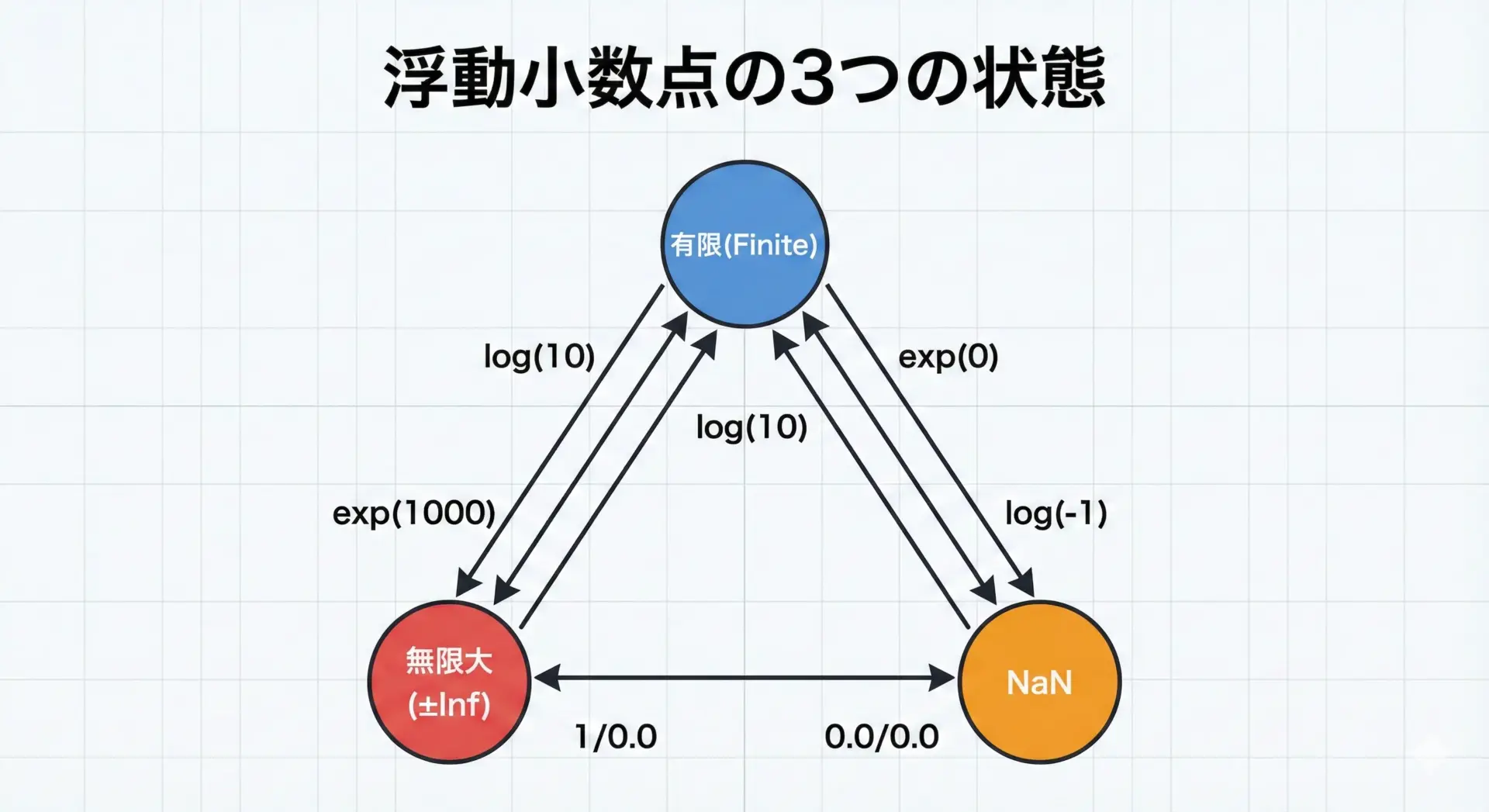

NaNや∞を早期に検出して処理を打ち切る・フォールバック処理に切り替えることで、後続の計算へエラーが連鎖するのを防げます。

オーバーフロー・アンダーフローを避ける実装テクニック

exp・logを安全に使ううえで、オーバーフロー・アンダーフローを避ける工夫は非常に重要です。

代表的なテクニックをいくつか紹介します。

事前の範囲チェックとクリッピング

expの場合、あらかじめxを安全な範囲に収めてしまう方法があります。

C言語

#include <math.h>

// double の exp でおおよそ安全な範囲(実装により異なります)
#define EXP_MAX 700.0
#define EXP_MIN -700.0

double safe_exp(double x) {
    if (x > EXP_MAX) {
        x = EXP_MAX;    // 上限にクリップ
    } else if (x < EXP_MIN) {
        x = EXP_MIN;    // 下限にクリップ
    }
    return exp(x);
}

このように入力をクリップすれば、オーバーフローによる∞やアンダーフローによる0を事実上防げます。

ただし、値を丸めることになるため、どの程度の誤差が許容されるかは用途に応じて検討する必要があります。

log-sum-expのテクニック

確率分布などで、log(exp(a) + exp(b))のような計算を行うと、exp部分でオーバーフローしやすくなります。

そこで、log-sum-expという変形テクニックを使います。

log(exp(a) + exp(b)) = m + log(exp(a - m) + exp(b - m)) ここでm = max(a, b)とします。

C言語

#include <stdio.h>
#include <math.h>

// 2つの値 a, b に対する log(exp(a) + exp(b)) を安全に計算
double log_sum_exp(double a, double b) {
    double m = (a > b) ? a : b;
    return m + log(exp(a - m) + exp(b - m));
}

int main(void) {
    double a = 1000.0;
    double b = 1001.0;

    // 直接計算すると exp(1000) や exp(1001) がオーバーフローする可能性が高い
    double lse = log_sum_exp(a, b);
    printf("log_sum_exp(%f, %f) = %f\n", a, b, lse);

    return 0;
}

実行結果

log_sum_exp(1000.000000, 1001.000000) = 1001.313262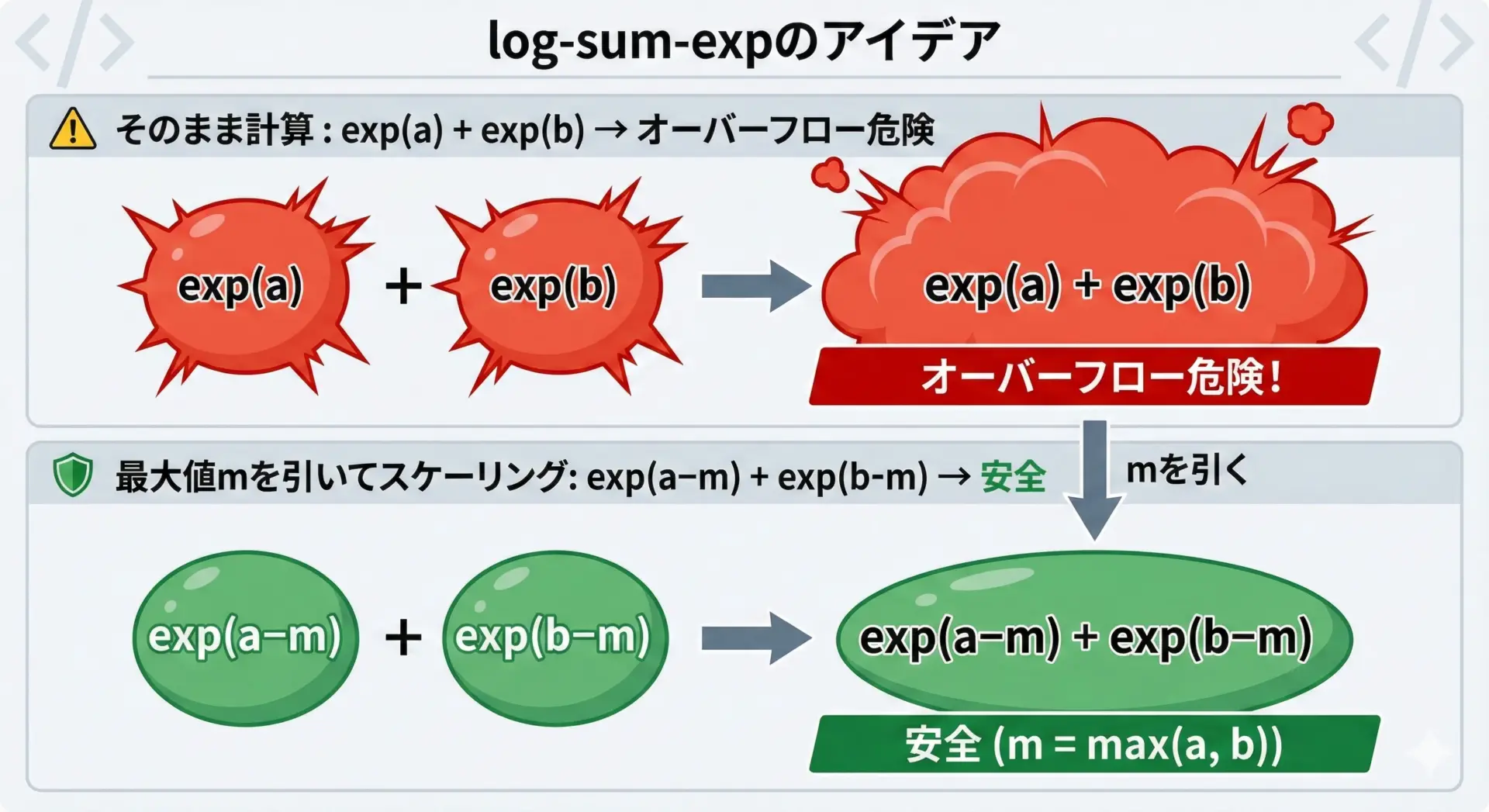

このような「最大値を引いてからexpを取る」手法は、機械学習や統計モデリングで頻繁に使われます。

精度誤差への対処

浮動小数点演算には、必ず丸め誤差が付きまといます。

exp・logも例外ではなく、特に次のようなケースで誤差が目立つことがあります。

非常に小さい値の差分log(1 + x)で、xが極端に小さい
非常に大きい・小さい値でのlog・exp
複数回のexpとlogの反復適用

標準ライブラリには精度改善のための関数もいくつか用意されています。

たとえばlog1p(x)はlog(1 + x)を高精度で計算する関数です。

C言語

#include <stdio.h>
#include <math.h>

int main(void) {
    double x = 1e-10;

    double y1 = log(1.0 + x);   // 通常の log
    double y2 = log1p(x);       // 精度改善版

    printf("log(1 + x)  = %.20f\n", y1);
    printf("log1p(x)    = %.20f\n", y2);
    printf("difference  = %.20e\n", y2 - y1);

    return 0;
}

実行結果

log(1 + x)  = 0.00000000010000000001
log1p(x)    = 0.00000000009999999999
difference  = -1.8873791419e-17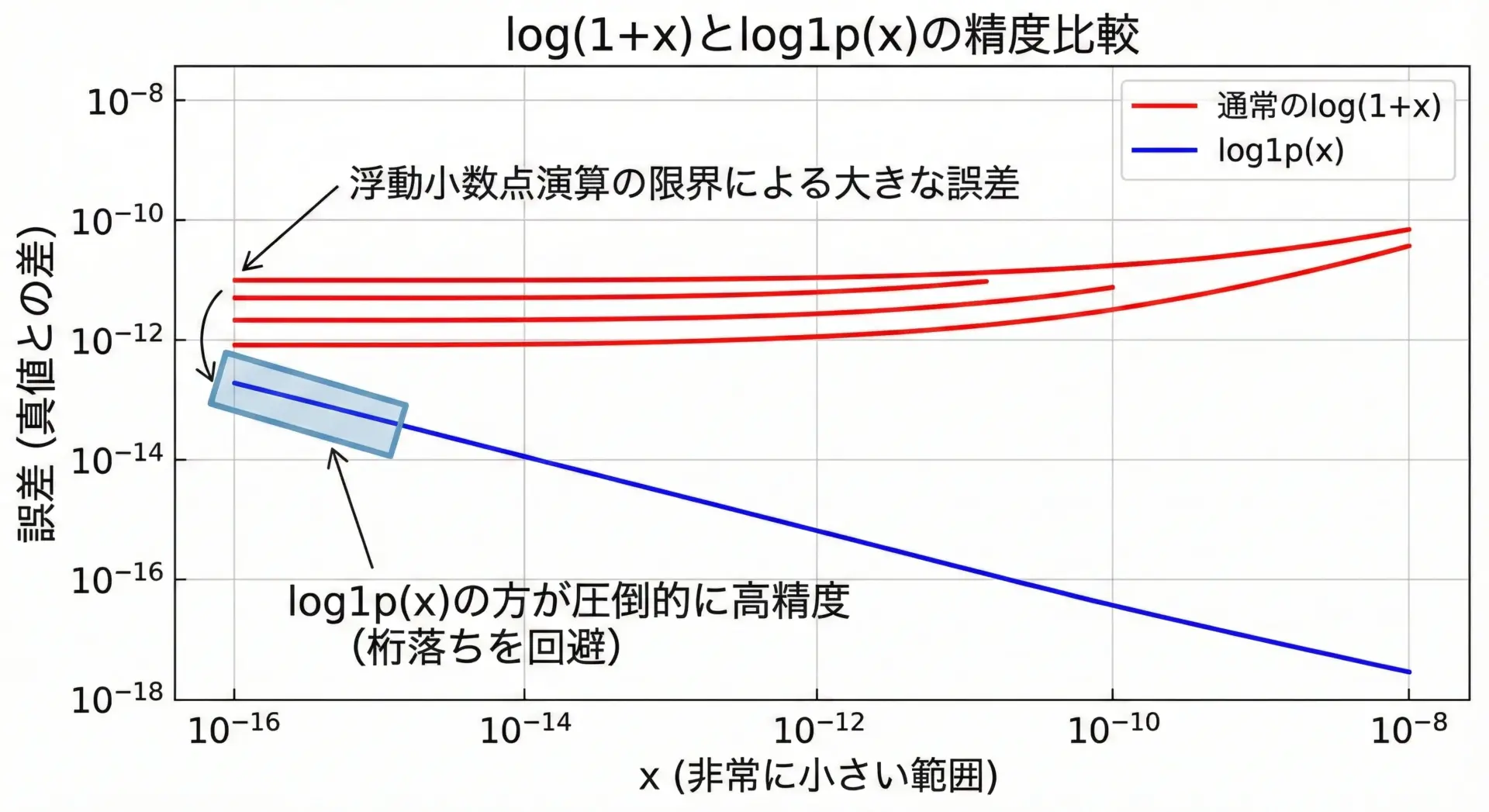

このような「特殊用途向けの数学関数」を知っておくと、数値誤差を抑えた堅牢な実装が可能になります。

C言語でexp・logを安全に使うためのチェックリスト

最後に、実務でexp・logを使用するときに意識しておきたいポイントをチェックリスト形式でまとめます。

文章として整理すると次のようになります。

まず、引数の範囲確認が最も重要です。

logに渡す値についてはx > 0かどうか必ずチェックし、0や負の値が入りうる場合には事前に弾くか、NaNを返すなど方針を決めておきます。

expについては、あまりに大きな正の値や非常に小さな負の値をそのまま渡さず、安全な範囲にクリップすることを検討します。

次に、戻り値の検証も欠かせません。

exp・logの結果についてisfiniteやisnanを用いて、無限大やNaNになっていないかチェックします。

重要な計算の直後にはerrnoの値も確認し、EDOMやERANGEが出ていないかを見るようにします。

さらに、数値安定性の観点から、明らかにオーバーフロー・アンダーフローを起こしやすい式は変形します。

例えば、log-sum-expのように最大値を引いてからexpを取る、分子・分母そろって非常に小さい値の割り算はlog差に置き換えるなどです。

加えて、型の一貫性にも注意が必要です。

floatの配列を扱っているのにexp(double版)を混在させると、暗黙の型変換によって予期しない精度変化を生むことがあります。

配列や構造体のメンバー型に合わせて、expf/logf や expl/logl を明示的に選ぶことが大切です。

最後に、誤差を許容する設計を心がけることも重要です。

浮動小数点で計算する以上、完全な一致を前提にした比較(a == bのような判定)には注意が必要で、適切な許容誤差(イプシロン)を設けた比較(fabs(a - b) < eps)を使うべきです。

exp・logを多用する計算では、誤差が累積しやすいため、アルゴリズム全体として誤差に強い設計を行うことが望まれます。

まとめ

exp・logは、C言語で数値計算を行ううえで欠かせない基本関数です。

expはeのx乗を、logは自然対数を表し、互いに逆関数の関係にあります。

本記事では、それぞれの関数の使い方、float・long double版との違い、常用対数log10、指数方程式の解き方、powとの組み合わせまでを解説しました。

加えて、オーバーフロー・アンダーフローや定義域エラーに対する対策として、errnoやisnan/isfiniteによるチェック、log-sum-expといった数値安定化テクニックも紹介しました。

これらのポイントを押さえておけば、C言語でexp・logを安全かつ効果的に活用できるはずです。