C言語で累乗(べき乗)を計算するとき、多くの人がまず思い浮かべるのがpow関数です。
しかし、powは「何となく使う」と危ない関数でもあり、特に整数計算では思わぬ誤差やバグを招きます。
この記事では、pow関数の基本から、整数計算での落とし穴、安全な代替手段まで、図解とサンプルコードで丁寧に解説します。
pow関数とは|C言語でべき乗計算を行う基本
pow関数の概要と書式
まず、pow関数が何をする関数なのかを整理します。
pow関数は、浮動小数点数の累乗(べき乗)を計算する標準ライブラリ関数です。
一般的な書式は次のようになります。
#include <math.h>
double pow(double x, double y);ここで、xは底(もと)となる値、yは指数です。
数学的にはx^y、つまり「xのy乗」を表します。
pow関数の戻り値は常にdouble型です。
引数に整数リテラルを渡しても、内部ではdouble型に変換されて計算される点が重要です。
powと四則演算の違い
通常の四則演算と違い、powは「回数が変化する乗算」をまとめて表現できる関数です。
例えば2 * 2 * 2 * 2はpow(2, 4)と書けます。
ただし、powは演算コストが比較的高いため、指数が小さいときには掛け算を繰り返す方が速く、かつ誤差が少ない場合も多いです。
この点は後半のパフォーマンスの章で詳しく扱います。
pow関数が定義されているヘッダファイル
pow関数は、C標準ライブラリのmath.hで定義されています。
そのため、利用するには必ずヘッダをインクルードする必要があります。
#include <stdio.h>
#include <math.h>
int main(void) {
double a = 2.0;
double b = 3.0;
double result = pow(a, b); // 2.0の3乗
printf("2.0^3.0 = %f\n", result);
return 0;
}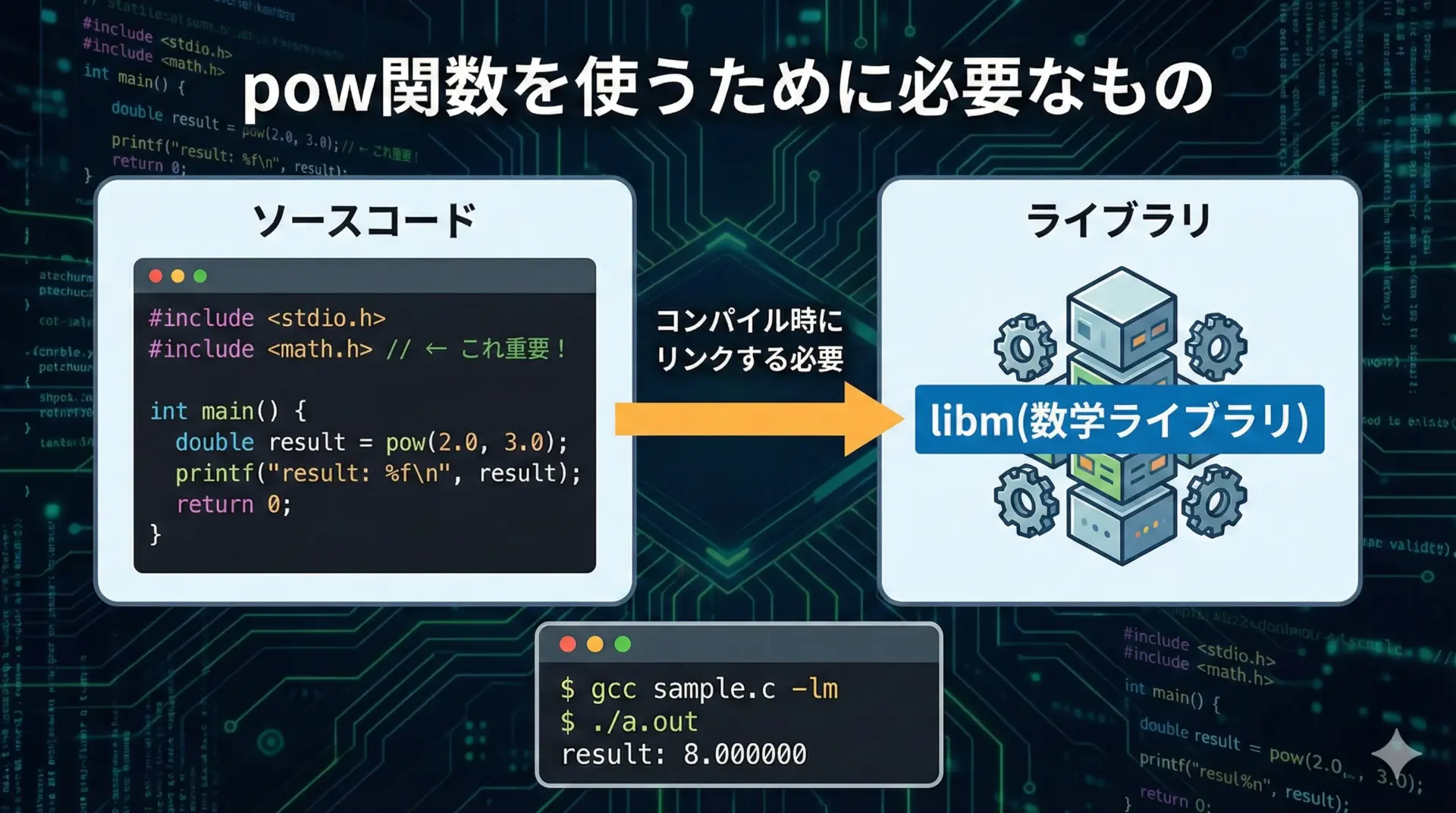
多くの環境では、コンパイル時に-lmオプションで数学ライブラリをリンクする必要があります。
例としてGCCでは次のようにコンパイルします。
gcc main.c -o main -lmこの-lmを付け忘れると、リンクエラー(未定義参照)になることがありますので注意してください。
pow関数と累乗(べき乗)計算の基本的な考え方
累乗(べき乗)は、同じ数を何回も掛け合わせる演算です。
例えば2^3は2 * 2 * 2を意味します。
pow関数では、このべき乗を1つの関数呼び出しで表現します。
pow(2.0, 3.0)→ 2.0の3乗 → 8.0pow(10.0, -2.0)→ 10.0の-2乗 → 0.01pow(9.0, 0.5)→ 9.0の0.5乗 → √9 → 3.0
ここで指数は整数に限られず、実数(小数)も指定できる点が重要です。
つまり、powは単なる「掛け算の回数指定ツール」ではなく、指数が実数のときの数学的べき乗まで扱う関数です。
pow関数の基本的な使い方とサンプルコード
pow関数の基本的な使い方
基本的な使い方はとてもシンプルです。
底と指数を2つの引数として渡すだけです。
double result = pow(底, 指数);ここで、底と指数はdouble型に変換できる型であればよく、intなどの整数を渡すことも可能です。
ただし、結果は常にdoubleで返るため、代入先の型には気を付ける必要があります。
典型的な使用パターン
べき乗計算は、次のような場面でよく使われます。
- 面積や体積など、物理量の計算(例: 円の面積で
pow(r, 2)を使う) - 指数関数的な増加・減少の計算(例: 減衰、利息計算)
- 正規分布など、統計・確率の計算
- 数学関数を用いるアルゴリズム
これらはいずれも「実数の精度がそれなりに必要で、かつ値がとても大きくも小さくもなりうる」計算が多く、powの特徴と相性が良いケースです。
pow関数を使った簡単なサンプルコード
ここでは、いくつかのパターンをまとめて計算するサンプルを示します。
#include <stdio.h>
#include <math.h>
int main(void) {
// 1. 基本的な整数同士のべき乗
double a = pow(2, 3); // 2^3 = 8
// 2. 実数を底にしたべき乗
double b = pow(2.5, 2); // 2.5^2 = 6.25
// 3. 負の指数(逆数の計算)
double c = pow(10, -2); // 10^-2 = 0.01
// 4. 小数の指数(平方根・立方根など)
double d = pow(9, 0.5); // 9^0.5 = 3 (平方根)
double e = pow(8, 1.0/3); // 8^(1/3) ≒ 2 (立方根)
// 5. 0乗のパターン
double f = pow(5, 0); // 5^0 = 1
printf("2^3 = %f\n", a);
printf("2.5^2 = %f\n", b);
printf("10^-2 = %f\n", c);
printf("9^0.5 = %f\n", d);
printf("8^(1/3) = %f\n", e);
printf("5^0 = %f\n", f);
return 0;
}想定される出力結果は次のようになります。
2^3 = 8.000000
2.5^2 = 6.250000
10^-2 = 0.010000
9^0.5 = 3.000000
8^(1/3) = 2.000000
5^0 = 1.000000ここで注目すべき点は「整数だけを渡しても、結果は小数部を含む形で表示される」ということです。
これはpowがdoubleを返しているためです。
負の値や0を使ったpow関数の挙動
powでは、底や指数に0や負の値を指定した場合に、いくつか注意すべきパターンがあります。
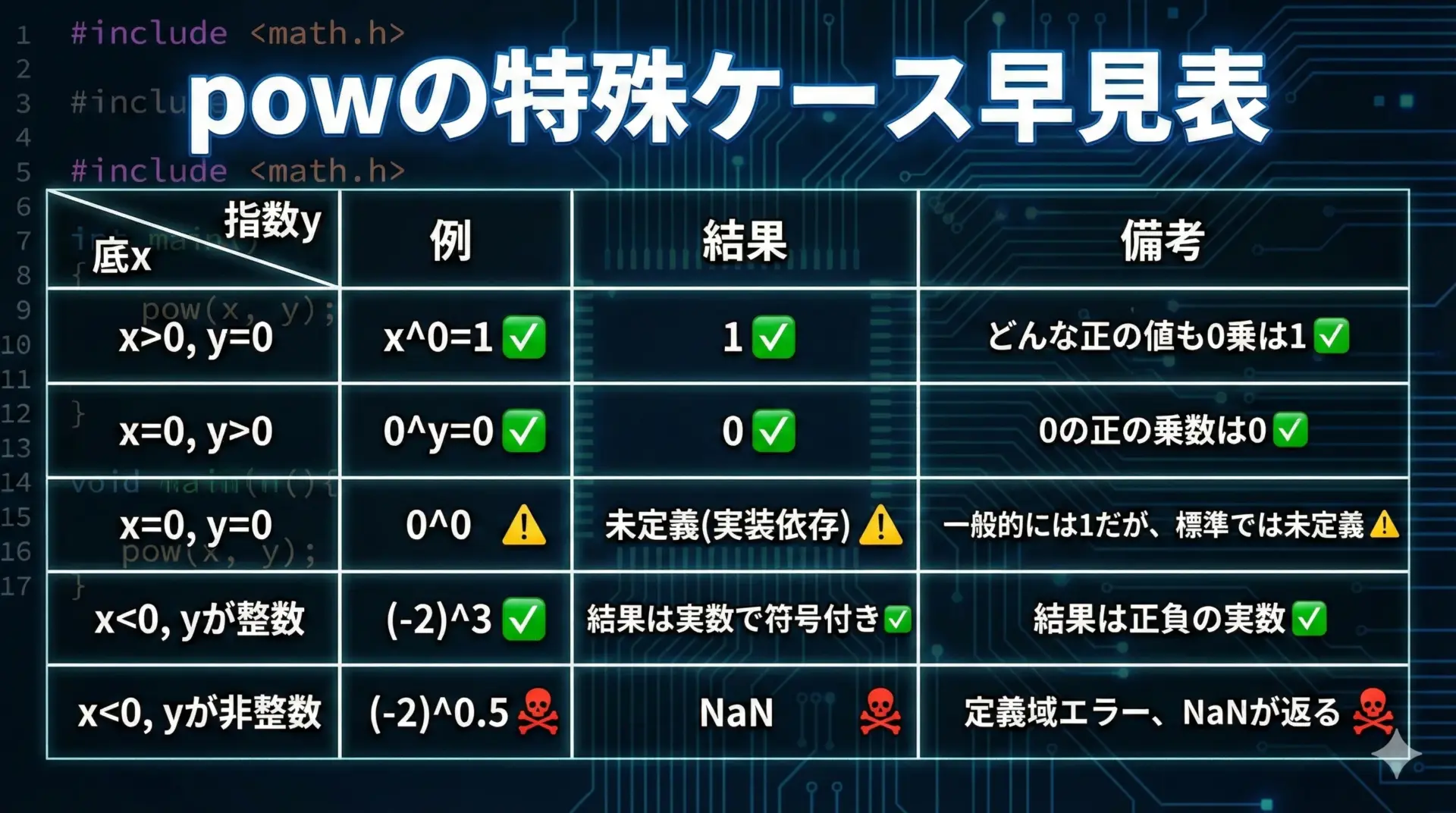
代表的なパターンを表にまとめます。
| 条件 | 例 | 結果の例 | 備考 |
|---|---|---|---|
| x > 0, y = 0 | pow(5, 0) | 1.0 | 任意の正数の0乗は1 |
| x = 0, y > 0 | pow(0, 3) | 0.0 | 0の正のべき乗は0 |
| x = 0, y = 0 | pow(0, 0) | 実装依存 | 数学的に未定義、避けるべき |
| x < 0, y が整数 | pow(-2, 3) | -8.0 | 奇数乗で負、偶数乗で正 |
| x < 0, y が整数でない(double) | pow(-2, 0.5) | NaN | 実数範囲では定義されない |
実際に動作を確認するコードを示します。
#include <stdio.h>
#include <math.h>
int main(void) {
printf("pow(5, 0) = %f\n", pow(5, 0)); // 5^0
printf("pow(0, 3) = %f\n", pow(0, 3)); // 0^3
printf("pow(-2, 3) = %f\n", pow(-2, 3)); // (-2)^3
printf("pow(-2, 2) = %f\n", pow(-2, 2)); // (-2)^2
printf("pow(-2, 0.5) = %f\n", pow(-2, 0.5)); // (-2)^0.5
// 0^0は避けるべきだが、動作を見るだけの例
printf("pow(0, 0) = %f (実装依存)\n", pow(0, 0));
return 0;
}出力例(環境によって多少異なります)。
pow(5, 0) = 1.000000
pow(0, 3) = 0.000000
pow(-2, 3) = -8.000000
pow(-2, 2) = 4.000000
pow(-2, 0.5) = -nan
pow(0, 0) = 1.000000 (実装依存)特にpow(0, 0)は数学的に未定義であり、環境によって結果が違い得るため、実務ではこのような呼び出しが発生しないように条件分岐で避けるのが安全です。
pow関数の戻り値とエラー時の注意点
powの戻り値はdoubleですが、計算できない場合やオーバーフローする場合には、特別な値が返されます。
代表的なものは次の通りです。
| 状況 | 戻り値の例 | 備考 |
|---|---|---|
| 領域外の実数(負数の平方根など) | NaN | Not a Number(数でない値) |
| オーバーフロー | HUGE_VAL など | 非常に大きな値で表現 |
| アンダーフロー | 0.0 に近い値 | 非常に小さい値に丸められる |
エラー判定を厳密に行う場合は、math.hのマクロやerrnoを用いることもありますが、日常的な用途では「NaNかどうか」「無限大かどうか」を判定する程度で十分な場合が多いです。
#include <stdio.h>
#include <math.h>
#include <errno.h>
int main(void) {
errno = 0;
double x = pow(-2.0, 0.5); // 本来は実数の範囲外
if (isnan(x)) { // NaNかどうかを判定
printf("結果はNaNです\n");
} else if (isinf(x)) { // 無限大かどうかを判定
printf("結果は無限大です\n");
} else {
printf("結果: %f\n", x);
}
if (errno != 0) {
printf("何らかのエラーが発生しました (errno=%d)\n", errno);
}
return 0;
}結果はNaNですpowの結果をそのまま信用せず、場合によってはNaNや無限大のチェックを行うことが、堅牢なプログラムには重要になります。
pow関数と整数計算の落とし穴
ここからが、実務や競技プログラミングで特に重要な部分です。
powはdoubleを返すため、整数の累乗計算に安易に使うとさまざまなトラブルが起こります。
pow関数は整数型ではなくdouble型を返す理由
powがdouble pow(double, double)という形をしているのは、「実数の指数まで含めた数学的なべき乗」を計算するためです。
もし戻り値がintであれば、次のような計算が扱えません。
pow(2.5, 3.7)pow(10, -1.5)pow(9, 0.5)(平方根)
また、指数が整数であっても、結果が小数になる場合が多くあります。
pow(2, -1)→ 0.5pow(3, -2)→ 1/9 ≒ 0.1111…
このように、powの設計思想は「実数計算」であり、「整数演算」は副次的な扱いと考えると理解しやすいです。
整数べき乗をpowで計算するときの誤差問題
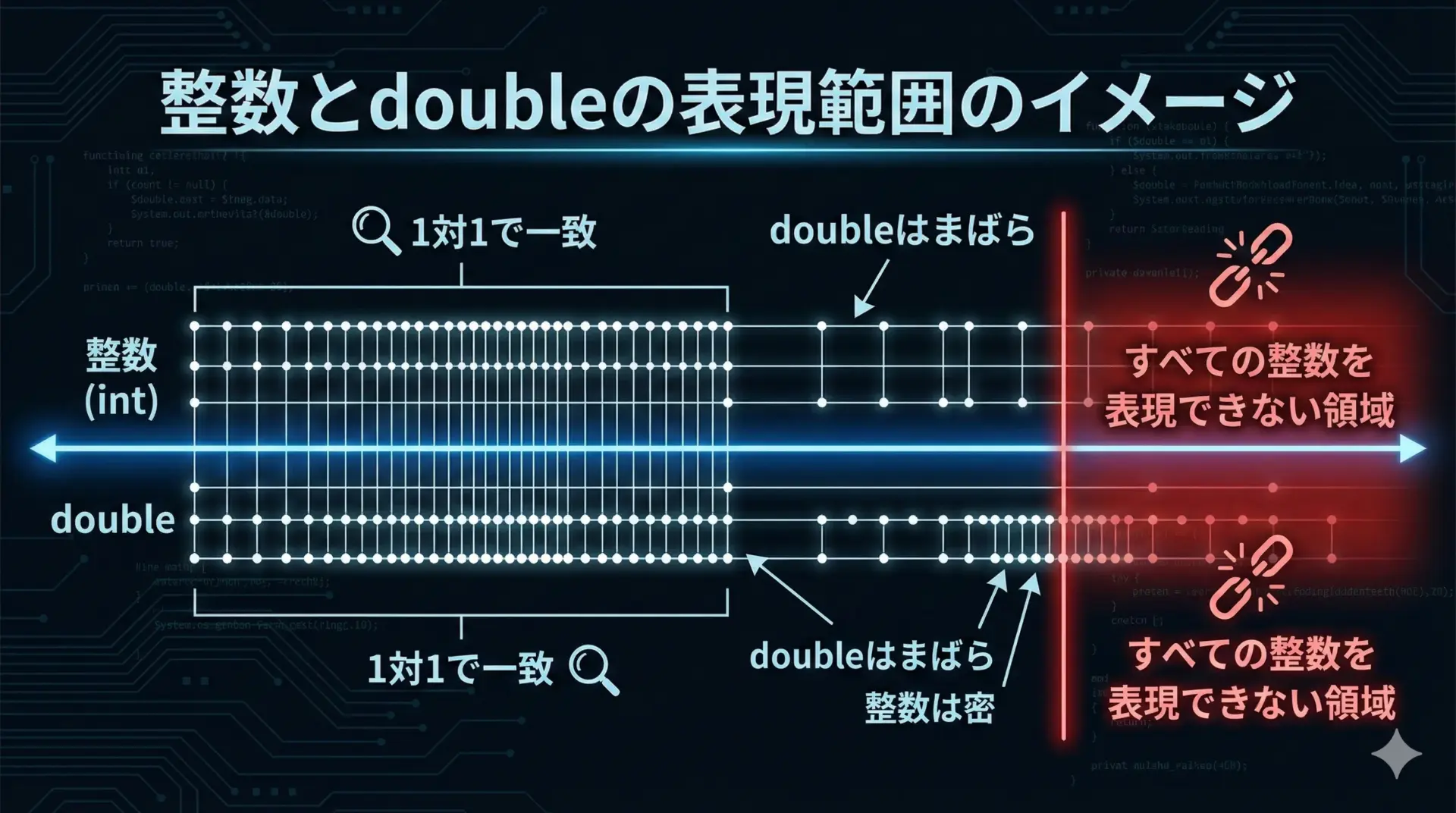
整数のべき乗をpowで計算し、(int)でキャストすれば良さそうに見えますが、ここに大きな落とし穴があります。
浮動小数点数(double)は全ての整数を正確に表現できるわけではなく、特に大きな値では誤差が発生しやすいためです。
例として、次のようなコードを見てみます。
#include <stdio.h>
#include <math.h>
int main(void) {
for (int i = 1; i <= 15; i++) {
double d = pow(3, i); // 3^i をdoubleで計算
int n = (int)d; // intにキャスト
printf("i=%2d: pow(3,%d)=%f, (int)=%d\n", i, i, d, n);
}
return 0;
}出力例(誤差が目立ち始めるのはもっと大きい指数ですが、例として):
i= 1: pow(3,1)=3.000000, (int)=3
i= 2: pow(3,2)=9.000000, (int)=9
i= 3: pow(3,3)=27.000000, (int)=27
...
i=15: pow(3,15)=14348907.000000, (int)=14348907この程度の範囲では問題がなさそうに見えますが、さらに大きな指数では危険になります。
例えば64ビット符号付き整数long longの範囲近くまで行くと、doubleでは隣り合う整数を区別できなくなるため、本来の値から1ずれた値になってしまうことがあります。
キャスト(int)pow(…)で起こりやすいバグ例
整数計算でありがちな「一見正しそうに見えて危険」なパターンを見てみます。
典型的なバグパターン
「nが10のべき乗かどうかを判定したい」というコードを、次のように書いてしまうことがあります。
#include <stdio.h>
#include <math.h>
/*
* nが10^k(10のべき乗)かどうかを判定するつもりの関数
* 実際には誤判定を起こしうる危険な例です。
*/
int is_power_of_10(int n) {
for (int k = 0; k <= 9; k++) {
int p = (int)pow(10, k); // 10^k を計算
if (p == n) {
return 1; // 一致したらtrue
}
}
return 0;
}
int main(void) {
for (int x = 1; x <= 1000000000; x *= 10) {
printf("%d: %s\n", x, is_power_of_10(x) ? "OK" : "NG");
}
return 0;
}このコードは、多くの環境では「たまたま」全てOKになるかもしれません。
しかし、環境や最適化レベル、コンパイラの実装によっては誤判定を起こす可能性があります。
さらに悪い例として、「k桁の最大値を求める」ために(int)pow(10, k) - 1を使うパターンがあります。
これも、powの誤差が原因で本来より1大きい/小さい値になることがあります。
こうしたバグはテストではなかなか再現せず、本番で条件が揃ったときにだけ顔を出すため、非常に厄介です。
オーバーフローと桁あふれに注意すべきケース
整数のべき乗は値の増え方が非常に急激であり、すぐに型の上限を超えてしまいます。
特にintやlong longを使うときは、オーバーフローの危険に注意が必要です。
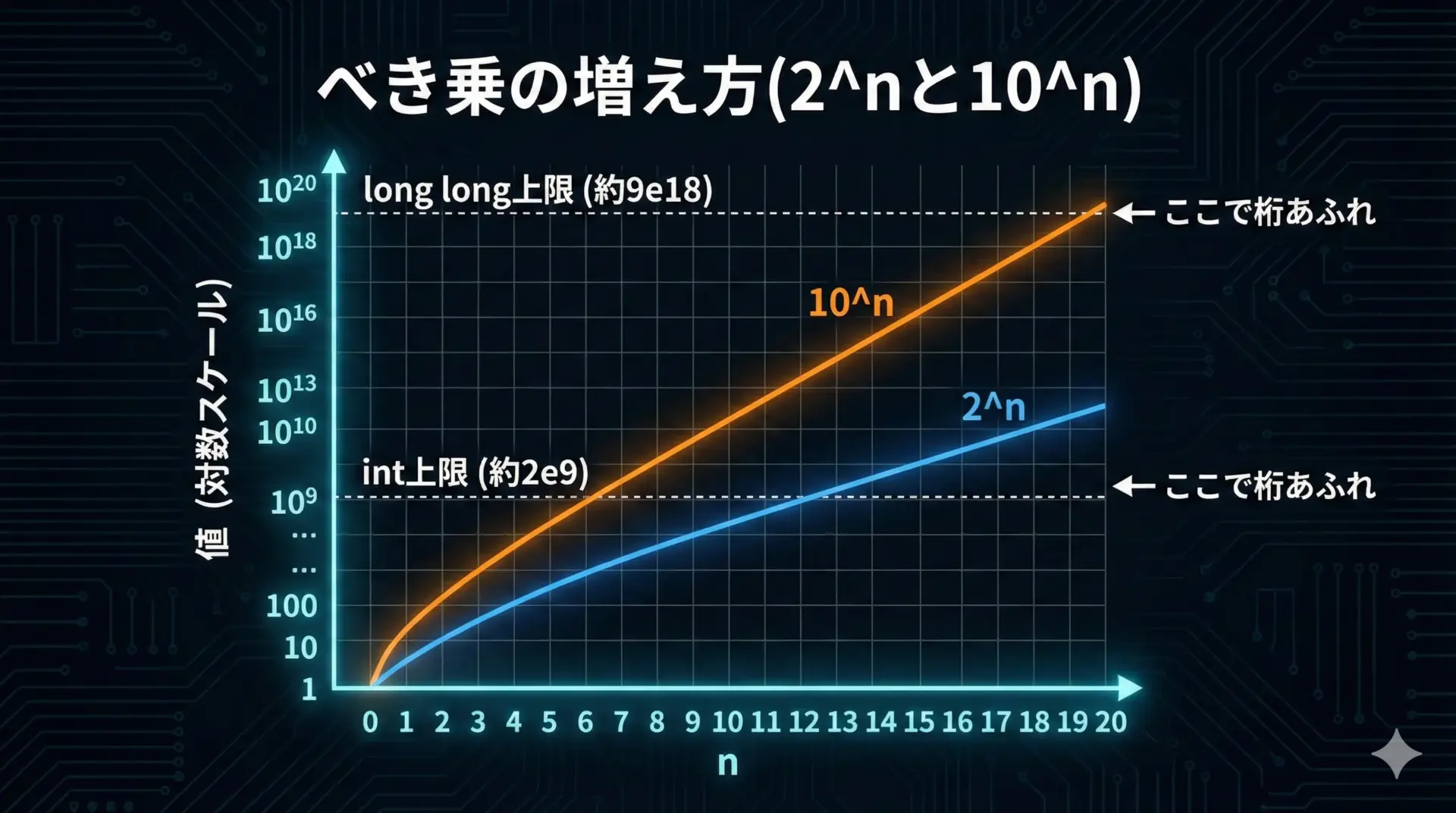
代表的な範囲を表にしておきます。
| 型 | およその最大値 | 10のべき乗での上限の目安 |
|---|---|---|
| 32bit int | 約 2 × 10^9 | 10^9 までが限界 |
| 64bit long long | 約 9 × 10^18 | 10^18 までが限界 |
例えば、int x = pow(10, 10);のようなコードは、計算結果がintの範囲を超えるため、未定義動作を引き起こします。
#include <stdio.h>
#include <math.h>
int main(void) {
double d = pow(10, 10); // doubleとしてはOK
int x = (int)d; // intにキャスト(オーバーフローの危険)
printf("double: %f\n", d);
printf("int : %d (未定義動作の可能性)\n", x);
return 0;
}このように、doubleでは表現できても、intやlong longでは表現できないというケースがいくらでもあります。
「powで計算したから大丈夫」ではないという点を強く意識する必要があります。
ループでの整数累乗計算との違いと向き不向き
整数のべき乗計算には、pow以外にも「ループで掛け算を繰り返す」という方法があります。
#include <stdio.h>
/*
* base^exp を整数として計算する単純な関数
* expは0以上と仮定します。
*/
int int_pow_loop(int base, int exp) {
int result = 1;
for (int i = 0; i < exp; i++) {
result *= base;
}
return result;
}
int main(void) {
for (int e = 0; e <= 10; e++) {
int x = int_pow_loop(2, e);
printf("2^%d = %d\n", e, x);
}
return 0;
}2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256
2^9 = 512
2^10 = 1024この方法にもオーバーフローの問題はありますが、計算自体は整数のまま行われるため、pow+キャストより予測しやすい特性があります。
用途による向き不向きは次のように整理できます。
| 用途 | powの利用 | ループによる整数計算 |
|---|---|---|
| 実数のべき乗(統計・物理計算など) | 向いている | 不向き |
| 小さな指数の単純な整数べき乗 | 微妙 | 向いている |
| 大きな整数べき乗(誤差許容なし) | 不向き | 自前実装が必須 |
| 2のべき乗など、特定の底 | 不向き | シフト演算が有利 |
整数べき乗で誤差が許されない場合、powは避けるという方針を基本にすると、安全な設計につながります。
pow関数の代替手段と安全なべき乗計算のコツ
ここまでの内容から、「どんなときにpowを使い、どんなときに避けるべきか」が見えてきます。
この章では、安全なべき乗計算の具体的な方法を整理します。
整数のべき乗は自前実装(int型・long long型)も選択肢
整数のべき乗を誤差なく計算したいなら、整数型で自前実装するのが基本です。
単純なループ版
すでに示したループ版を、long long対応で書き直しておきます。
#include <stdio.h>
/*
* base^exp を long long で計算する単純な関数
* expは0以上とします。
* オーバーフロー検出は行っていません。
*/
long long ll_pow_simple(long long base, int exp) {
long long result = 1;
for (int i = 0; i < exp; i++) {
result *= base;
}
return result;
}
int main(void) {
for (int e = 0; e <= 10; e++) {
long long x = ll_pow_simple(3, e);
printf("3^%d = %lld\n", e, x);
}
return 0;
}高速な二分累乗法(べき乗の二分法)
指数が大きくなる場合は、二分累乗法(バイナリ法)を使うと高速に計算できます。
#include <stdio.h>
/*
* base^exp を long long で計算する二分累乗法の実装例です。
* expは0以上とします。
*/
long long ll_pow_fast(long long base, long long exp) {
long long result = 1;
long long x = base;
long long e = exp;
while (e > 0) {
if (e & 1) {
// eの最下位ビットが1なら結果にxを掛ける
result *= x;
}
x *= x; // 底を二乗していく
e >>= 1; // 指数を1ビット右シフト(2で割る)
}
return result;
}
int main(void) {
long long base = 2;
for (int e = 0; e <= 20; e++) {
long long x = ll_pow_fast(base, e);
printf("%lld^%d = %lld\n", base, e, x);
}
return 0;
}2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
...
2^20 = 1048576このような自前実装であれば、演算が全て整数で行われ、誤差なく結果を得られる一方で、オーバーフローは自分で管理する必要があります。
必要に応じて、掛け算の前に上限をチェックするなどの工夫を行うとよいでしょう。
ビット演算(シフト)で2のべき乗を求める方法
底が2のときは、ビットシフト演算を使うと、powよりも高速で安全に計算できます。

C言語では(1 << n)が2^nに相当します。
#include <stdio.h>
/*
* 2のべき乗をビットシフトで計算する例です。
*/
int main(void) {
for (int n = 0; n <= 10; n++) {
int x = (1 << n); // 2^n に相当
printf("2^%d = %d\n", n, x);
}
return 0;
}2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256
2^9 = 512
2^10 = 1024「2のべき乗かどうかの判定」や「2のべき乗の列挙」は、powではなくビット演算で行うのが、Cプログラムでは一般的です。
powf・powlとの違い
C言語には、powの仲間としてpowfとpowlがあります。
これらは引数と戻り値の型が異なります。
| 関数名 | 引数の型 | 戻り値の型 | 主な用途 |
|---|---|---|---|
| pow | double, double | double | 通常の倍精度浮動小数点計算 |
| powf | float, float | float | 単精度浮動小数点計算 |
| powl | long double, long double | long double | 拡張精度浮動小数点計算(環境依存) |
#include <stdio.h>
#include <math.h>
int main(void) {
float xf = 2.0f, yf = 3.0f;
double xd = 2.0, yd = 3.0;
long double xl = 2.0L, yl = 3.0L;
float rf = powf(xf, yf); // float版
double rd = pow(xd, yd); // double版
long double rl = powl(xl, yl); // long double版
printf("powf : %f\n", rf);
printf("pow : %f\n", rd);
printf("powl : %Lf\n", rl);
return 0;
}powf : 8.000000
pow : 8.000000
powl : 8.000000整数計算に使うべきではないという点は、powf/powlでも同じです。
あくまで浮動小数点計算の精度とパフォーマンスを調整するためのバリエーションと考えてください。
パフォーマンスを意識したべき乗計算の考え方
べき乗計算は、アルゴリズムの中で何度も登場することがあり、その場合パフォーマンス(速度)も重要なポイントになります。
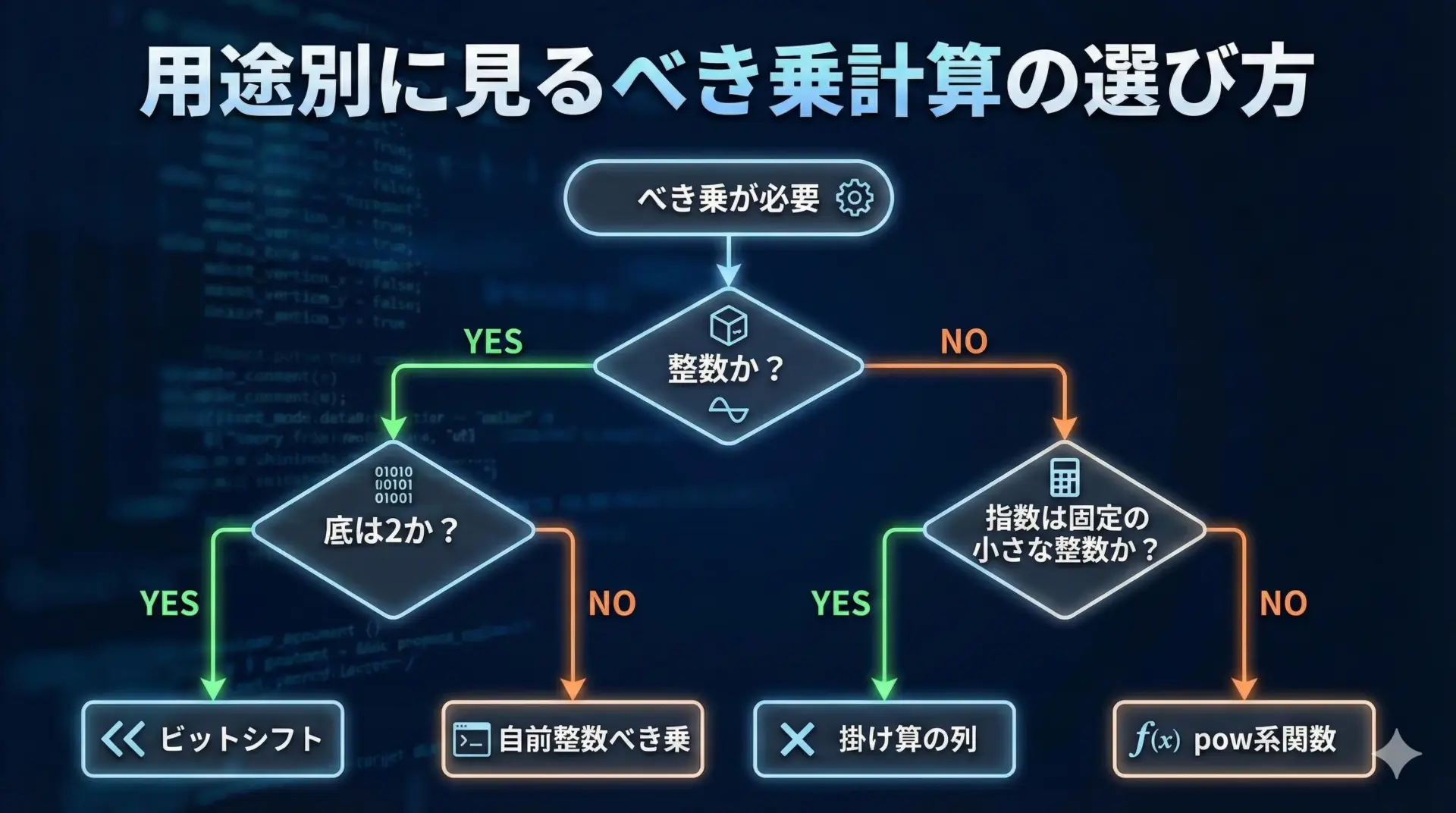
べき乗の用途ごとに、適切な手段を整理してみます。
- 実数の一般的なべき乗
指数が実数(小数)の場合や、指数が変化する場合は、pow/powf/powlの利用が妥当です。 - 小さな整数指数の固定計算
例えば「xの2乗」「xの3乗」など、指数が小さく固定されている場合は、powよりも単純な掛け算の方が速く、かつ誤差も少なくなります。// 悪い例 y = pow(x, 2); // 2乗 // 良い例 y = x * x; - 整数のべき乗で誤差が許されない場合
自前の整数べき乗関数(ループor二分累乗法)を使います。powは使いません。 - 2のべき乗
ビットシフト(1 << n)を使います。これは非常に高速で、整数のまま正確に計算できます。
このように、powは「万能のべき乗関数」ではなく、「実数のべき乗専用の道具」と考え、整数用途には代替手段を積極的に検討することが、パフォーマンスと正確性の両面で重要です。
まとめ
pow関数は、C言語でべき乗計算を行うための基本的な数学関数であり、実数のべき乗を簡潔に、幅広い範囲で扱える強力なツールです。
一方で、戻り値がdoubleであることから、整数べき乗に安易に使うと誤差やオーバーフロー、キャスト時のバグを招きやすいことも理解しておかなければなりません。
整数のべき乗では自前実装やビット演算を使い、実数の汎用的なべき乗にだけpowを使う、という役割分担を意識すると、安全で効率的なコードを書けます。
用途に応じて、pow・powf・powl・整数べき乗関数・ビットシフトを使い分けていきましょう。

