C言語で平方根を計算したいときに最初に登場するのがsqrt関数です。
単に平方根を求めるだけでなく、小数の扱い、エラー処理、移植性などを正しく押さえておかないと、思わぬバグや誤差につながります。
本記事では、C言語のsqrtの基本から応用、エラー処理までを一気に整理し、実践的に使いこなせるようになることを目指します。
sqrtとは?概要と基本仕様
sqrt関数とは
sqrt関数は、引数に与えた非負の実数の平方根を計算する標準数学ライブラリの関数です。
例えば、25の平方根は5、2.25の平方根は1.5というように、x * x = aとなるxを返す関数です。
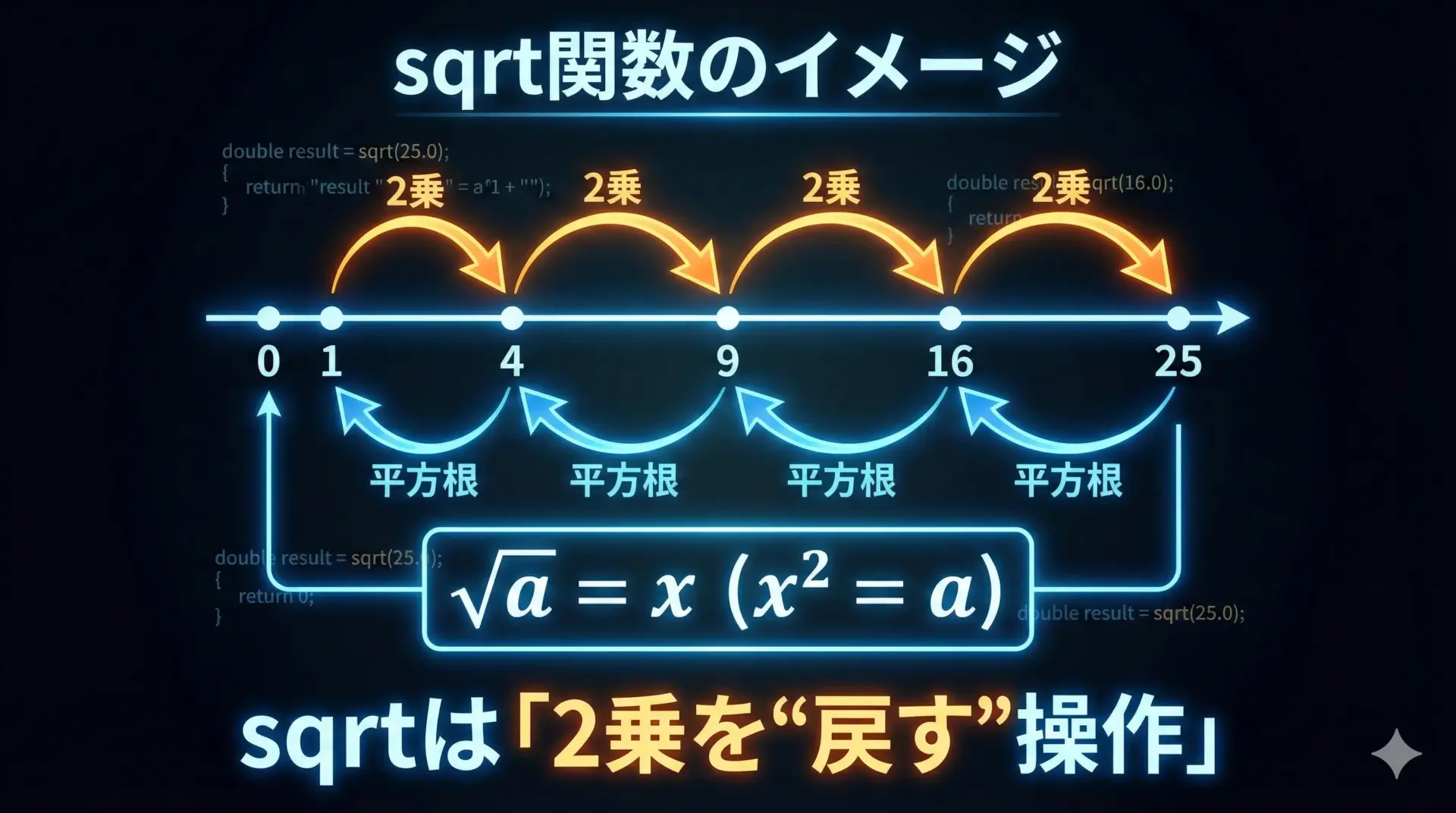
平方根というと数学的なイメージが強いですが、プログラムでは次のような場面で頻繁に使います。
- ベクトルの長さ(ノルム)の計算
- 2点間の距離(ユークリッド距離)の計算
- 標準偏差など統計量の計算
- 物理シミュレーションでの距離・速度の計算
そのため、ゲーム開発、数値計算、統計処理、機械学習など、幅広い分野で必須の関数だといえます。
sqrt関数の宣言とヘッダファイル
sqrtは標準Cの数学ライブラリmath.hに定義されています。
使用するには#includeでヘッダをインクルードし、必要に応じてリンク時に数学ライブラリを指定します。
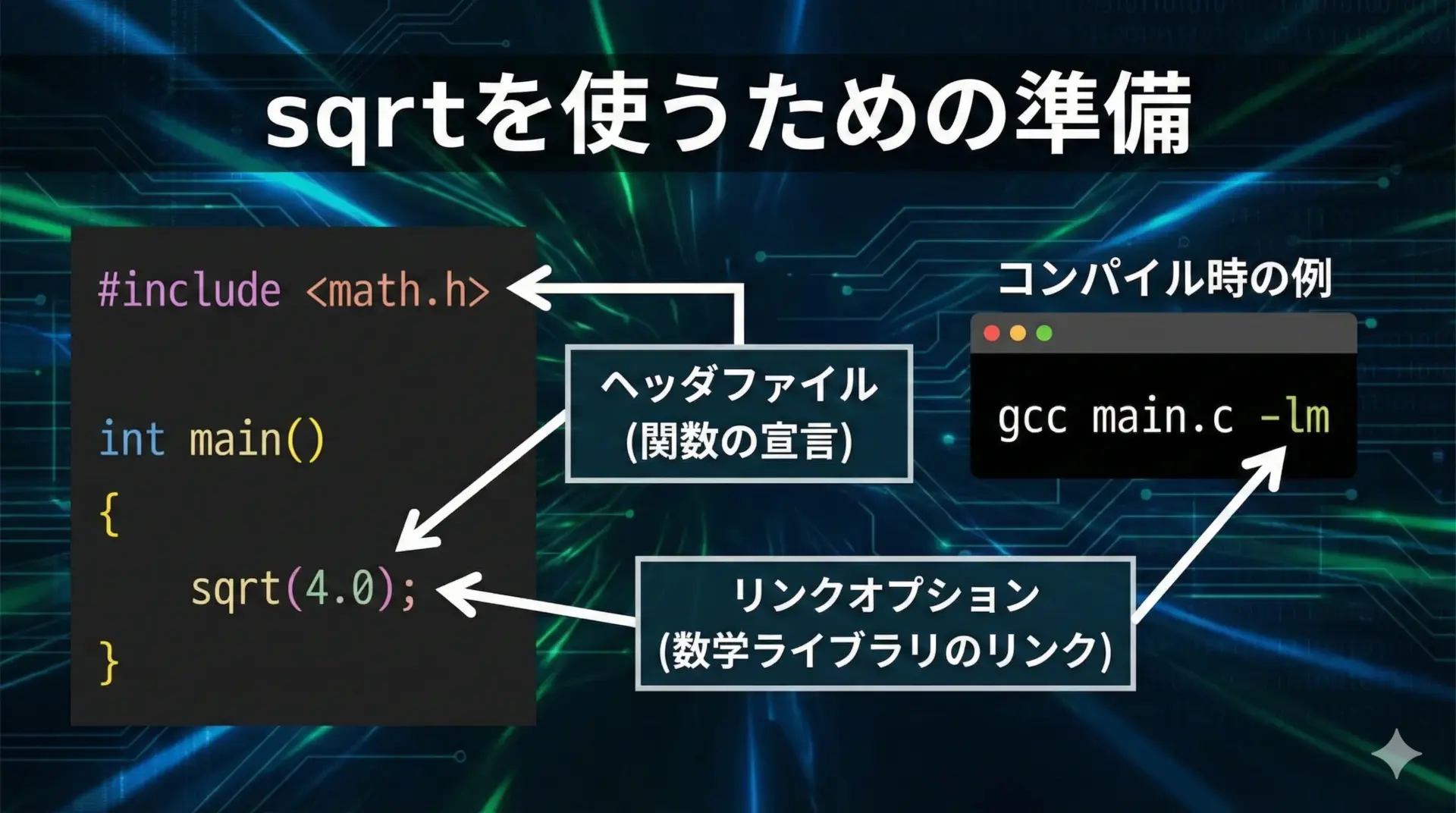
C言語でsqrtを使うときの最小構成は次のようになります。
#include <stdio.h> // printfを使うため
#include <math.h> // sqrtを使うため
int main(void) {
double x = 4.0;
double y = sqrt(x); // xの平方根を計算
printf("sqrt(%f) = %f\n", x, y);
return 0;
}多くのUnix系環境(gccなど)では、コンパイル時に-lmオプションで数学ライブラリをリンクする必要があります。
gcc main.c -o main -lmWindows環境(MSVCなど)では、通常は-lmの指定は不要です。
環境によって扱いが異なるため、使用しているコンパイラのマニュアルを確認することが大切です。
sqrtの返り値と戻り値の型
sqrtの宣言は、C99以降では次のようになっています。
double sqrt(double x);
float sqrtf(float x);
long double sqrtl(long double x);ここで重要なのは引数と戻り値の型が対応している点です。
sqrtはdouble版sqrtfはfloat版sqrtlはlong double版
まとめると、次のような対応になります。
| 関数名 | 引数の型 | 戻り値の型 | 主な用途 |
|---|---|---|---|
| sqrt | double | double | 一般的な倍精度計算 |
| sqrtf | float | float | 単精度で十分な場合、GPU向けなど |
| sqrtl | long double | long double | 高精度が必要な場合 |
C89ではsqrtのみが標準であり、sqrtfやsqrtlは存在しないか、実装依存の場合があります。
詳細は後半の「C89/C99でのsqrtの扱い」で説明します。
sqrtの基本的な使い方
sqrtの基本構文とサンプルコード
基本構文は非常にシンプルで、1つの実数引数を取り、その平方根を返すだけです。
戻り値の型 関数名(引数の型 引数名);つまりsqrtであればdouble sqrt(double x);です。
実際の使用例を見てみましょう。
#include <stdio.h>
#include <math.h>
int main(void) {
double a = 9.0;
double b = 2.25;
double result1 = sqrt(a); // 9.0の平方根 -> 3.0
double result2 = sqrt(b); // 2.25の平方根 -> 1.5
printf("sqrt(%f) = %f\n", a, result1);
printf("sqrt(%f) = %f\n", b, result2);
return 0;
}sqrt(9.000000) = 3.000000
sqrt(2.250000) = 1.500000整数リテラルを渡した場合でも、内部的には実数(double)に変換されてから計算されます。
そのため、sqrt(9)という書き方も可能ですが、戻り値の型はdoubleです。
整数の平方根を求めるときの注意点
整数の平方根を求めたいケースは多くありますが、sqrtはあくまで浮動小数点の関数であり、整数用ではないことに注意が必要です。
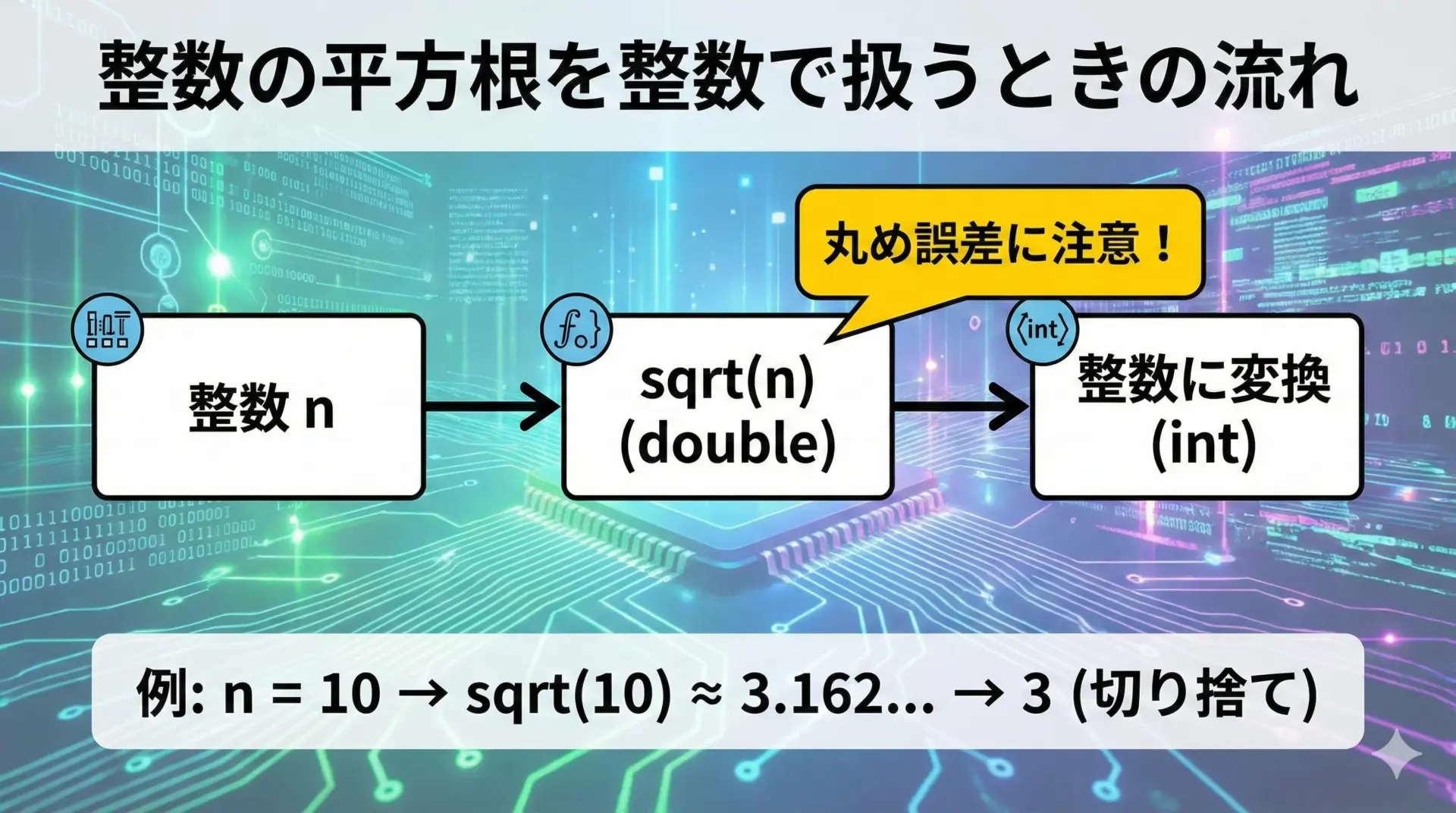
例えば、整数nの平方根を整数として扱いたい場合、次のようなコードを書くことが多いです。
#include <stdio.h>
#include <math.h>
int main(void) {
int n = 10;
double root = sqrt((double)n); // intをdoubleにキャストしてからsqrt
int root_int = (int)root; // 結果をintにキャストして整数に
printf("n = %d\n", n);
printf("sqrt(n) (double) = %f\n", root);
printf("sqrt(n) (int) = %d\n", root_int);
return 0;
}n = 10
sqrt(n) (double) = 3.162278
sqrt(n) (int) = 3ここでのポイントは次の通りです。
1. sqrtは整数ではなく実数(double)を返す 2. 整数として扱いたい場合はキャストや丸め処理が必要 3. 2乗して元に戻るとは限らない(丸め誤差のため)
このように、整数の平方根を扱うときは「どのように丸めるのか」(切り捨て、切り上げ、四捨五入)を明確に決めて、それに応じた処理を実装することが重要です。
丸め方法については後で詳しく説明します。
小数(浮動小数点)の平方根の計算方法
小数(浮動小数点)の平方根を計算する場合は、基本的にdouble型かfloat型を用います。
精度が特に問題にならない一般的な用途ではdoubleを使うのが無難です。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 2.0;
double y = 0.5;
double r1 = sqrt(x); // 2.0の平方根
double r2 = sqrt(y); // 0.5の平方根
printf("sqrt(%f) = %f\n", x, r1);
printf("sqrt(%f) = %f\n", y, r2);
// float版sqrtfを使う例
float xf = 2.0f;
float rf = sqrtf(xf); // float版
printf("sqrtf(%f) = %f\n", xf, rf);
return 0;
}sqrt(2.000000) = 1.414214
sqrt(0.500000) = 0.707107
sqrtf(2.000000) = 1.414214floatで十分な場合でも、内部での計算はしばしばdoubleで行われることがあります。
そのため、速度・メモリの制約が特にない限りはdoubleを使う設計が一般的です。
変数を使ったsqrtの活用例
sqrtの代表的な活用例として、2次元平面上の2点間の距離を求める問題を考えてみます。
これはゲーム開発やグラフィックス分野で頻繁に登場します。

距離の公式は次の通りです。
distance = sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
これをC言語で書くと次のようになります。
#include <stdio.h>
#include <math.h>
// 2次元平面上の2点間の距離を計算するプログラム
int main(void) {
double x1 = 1.0, y1 = 2.0; // 点Aの座標
double x2 = 4.0, y2 = 6.0; // 点Bの座標
double dx = x2 - x1; // x方向の差
double dy = y2 - y1; // y方向の差
// 距離 = sqrt(dx^2 + dy^2)
double distance = sqrt(dx * dx + dy * dy);
printf("A(%.1f, %.1f), B(%.1f, %.1f)\n", x1, y1, x2, y2);
printf("dx = %.1f, dy = %.1f\n", dx, dy);
printf("distance = %f\n", distance);
return 0;
}出力の一例は次の通りです。
A(1.0, 2.0), B(4.0, 6.0)
dx = 3.0, dy = 4.0
distance = 5.000000このように「差を2乗して足し合わせ、その平方根を取る」というパターンは非常によく使われるため、sqrtとセットで覚えておくと便利です。
sqrtの応用と注意点
負の値をsqrtに渡したときの挙動とエラー
実数の世界では、負の数の平方根は定義されません(複素数の話は一旦除きます)。
そのため、sqrtに負の値を渡すとエラー的な挙動になります。
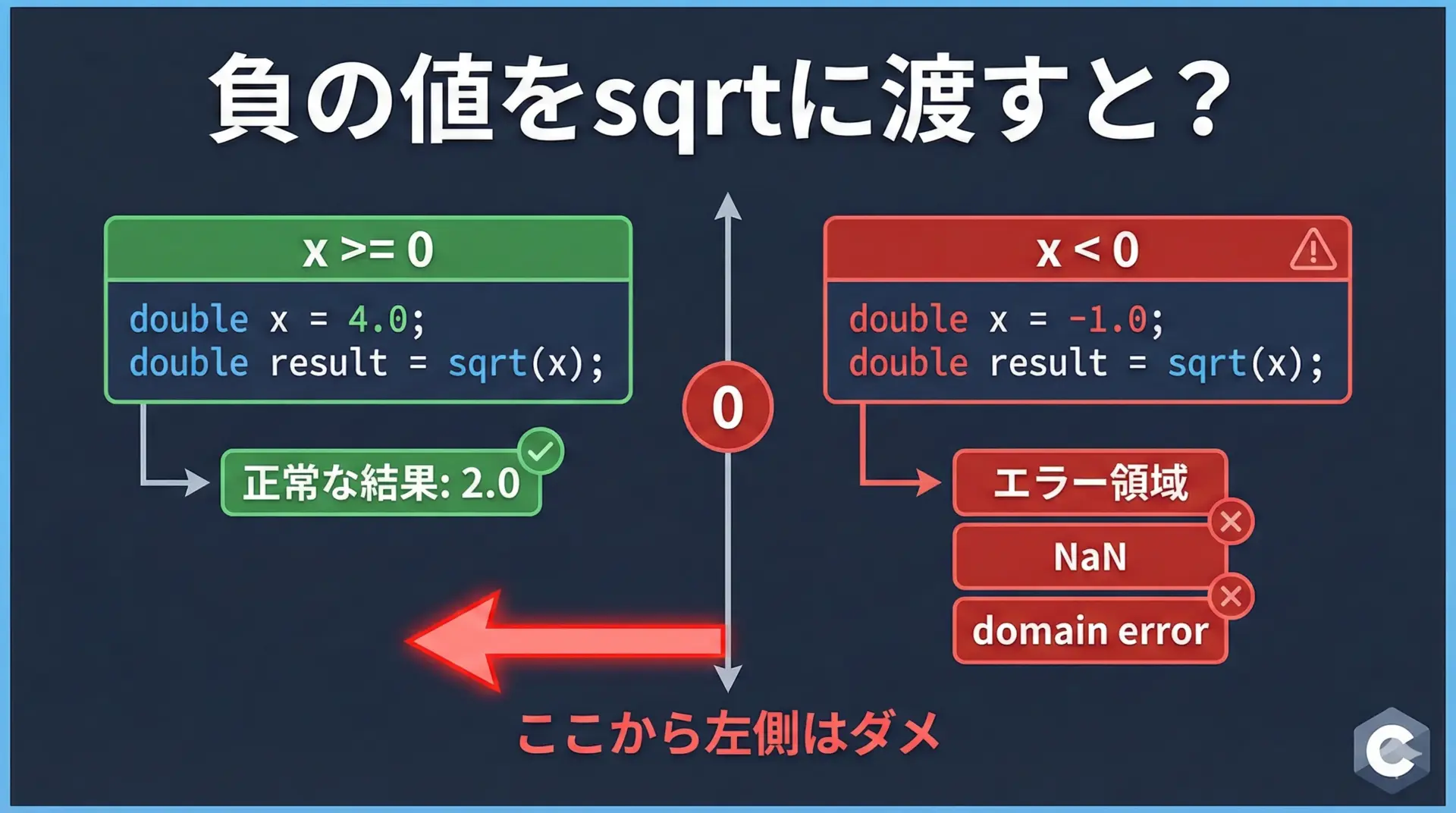
実際に負の値を渡してみるコード例です。
#include <stdio.h>
#include <math.h>
#include <errno.h> // errnoを使うため
int main(void) {
double x = -4.0;
errno = 0; // errnoを0で初期化
double r = sqrt(x); // 負の値の平方根を計算しようとする
printf("sqrt(%f) = %f\n", x, r);
printf("errno = %d\n", errno);
return 0;
}出力は環境によって異なりますが、例えば次のようになることがあります。
sqrt(-4.000000) = nan
errno = 33ここでのポイントは次の通りです。
- 戻り値が
NaN(Not a Number)になることが多い errnoにEDOM(domain error)がセットされる実装がある- ただし挙動は処理系依存の部分があり、必ずしも同じとは限らない
このため、負の値を渡さないように事前チェックするか、後述するisnanで結果を検査するなどの対策を行うことが大切です。
sqrtとNaN・infの関係
浮動小数点には、普通の数値とは別に「特別な値」としてNaNとinfがあります。
NaN(Not a Number): 計算不能な結果などを表す特別な値infまたは+∞: 正の無限大-infまたは-∞: 負の無限大
sqrtにこれらの値を渡した場合の挙動は、IEEE 754に準拠した環境では次のようになることが多いです。
| 入力 x | sqrt(x) の結果 |
|---|---|
| 正の有限値 | その平方根 |
| 0 | 0 |
| 正の無限大 inf | 正の無限大 inf |
| NaN | NaN |
| 負の有限値 | NaN (domain error) |
| 負の無限大 -inf | NaN (domain error) |
例えば、次のようなコードで挙動を確認できます。
#include <stdio.h>
#include <math.h>
int main(void) {
double zero = 0.0;
double pos_inf = 1.0 / zero; // +inf
double neg_inf = -1.0 / zero; // -inf
double nan_val = zero / zero; // NaN
printf("sqrt(0.0) = %f\n", sqrt(zero));
printf("sqrt(+inf) = %f\n", sqrt(pos_inf));
printf("sqrt(-inf) = %f\n", sqrt(neg_inf));
printf("sqrt(NaN) = %f\n", sqrt(nan_val));
return 0;
}表示上はinfやnanなどと出力されることが多いです。
これらの判定には、後述するisnanやisinfを使います。
sqrtの誤差と浮動小数点の丸め誤差
浮動小数点は有限のビット数で実数を近似表現しているため、どうしても丸め誤差が発生します。
sqrtも例外ではなく、理論値とわずかに異なる結果になることがあります。
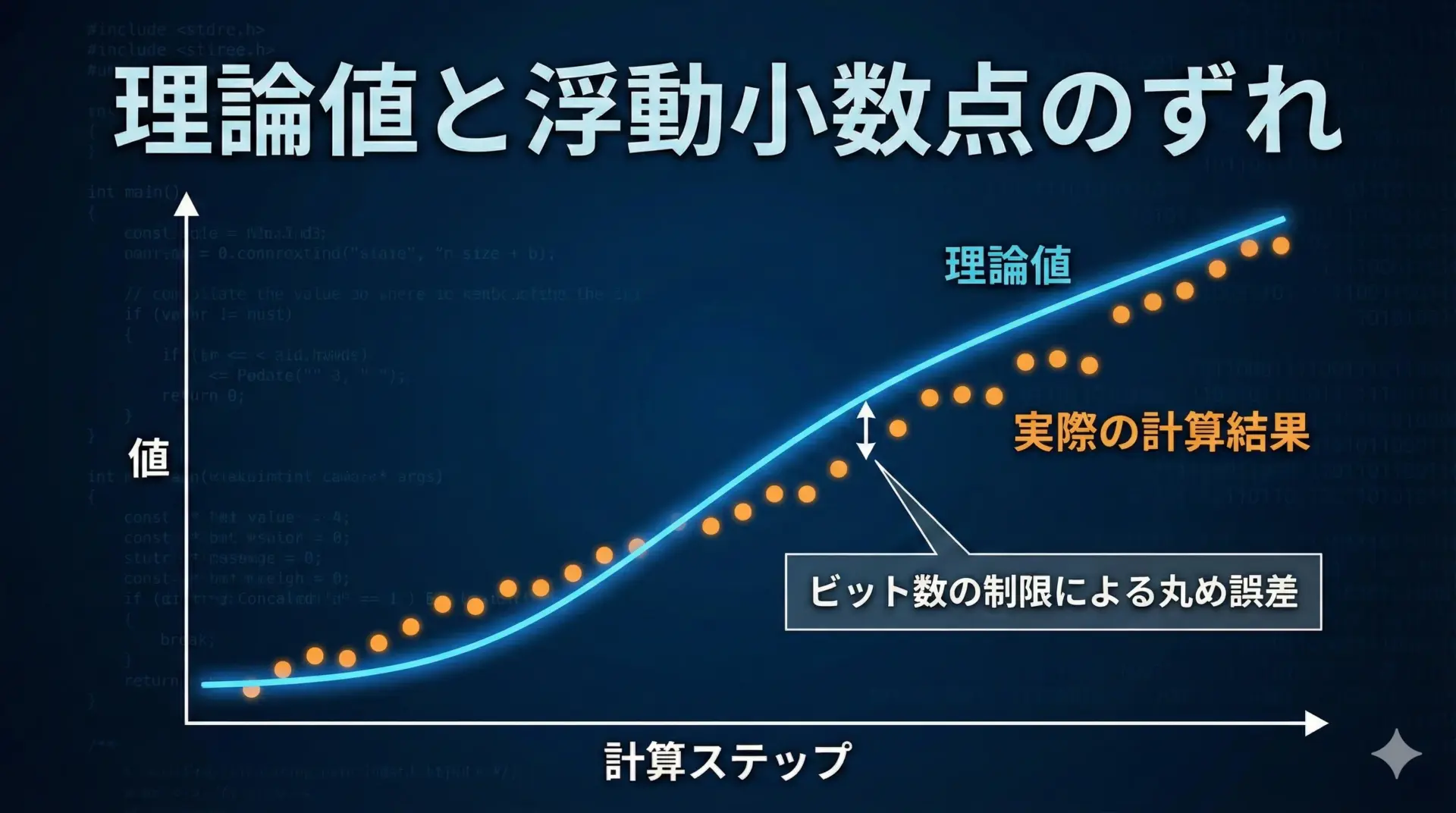
例えば、sqrt(2.0)の結果は無限小数になりますが、コンピュータでは有限桁に丸めて表現します。
そのため、sqrt(2.0) * sqrt(2.0)を計算しても、必ずしも2.0には戻りません。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 2.0;
double r = sqrt(x);
double back = r * r;
printf("sqrt(2.0) = %.17f\n", r);
printf("sqrt(2.0)^2 = %.17f\n", back);
return 0;
}出力の一例は次のようになります。
sqrt(2.0) = 1.4142135623730951
sqrt(2.0)^2 = 2.0000000000000004見た目にはほとんど2ですが、厳密には2.0000000000000004になっています。
この微小な差が比較処理などで問題になることがあります。
このため、浮動小数点の比較では「完全一致」ではなく「誤差を許容した比較」を行うのが一般的です。
例えば、ある許容誤差epsを用いてfabs(a - b) < epsかどうかで比較する方法がよく使われます。
sqrtの結果を整数に切り捨てる・四捨五入する方法
平方根の結果を整数として扱いたい場合、どのように丸めるかを明確にすることが重要です。
ここでは、代表的な3つの方法を紹介します。
- 切り捨て
- 切り上げ
- 四捨五入
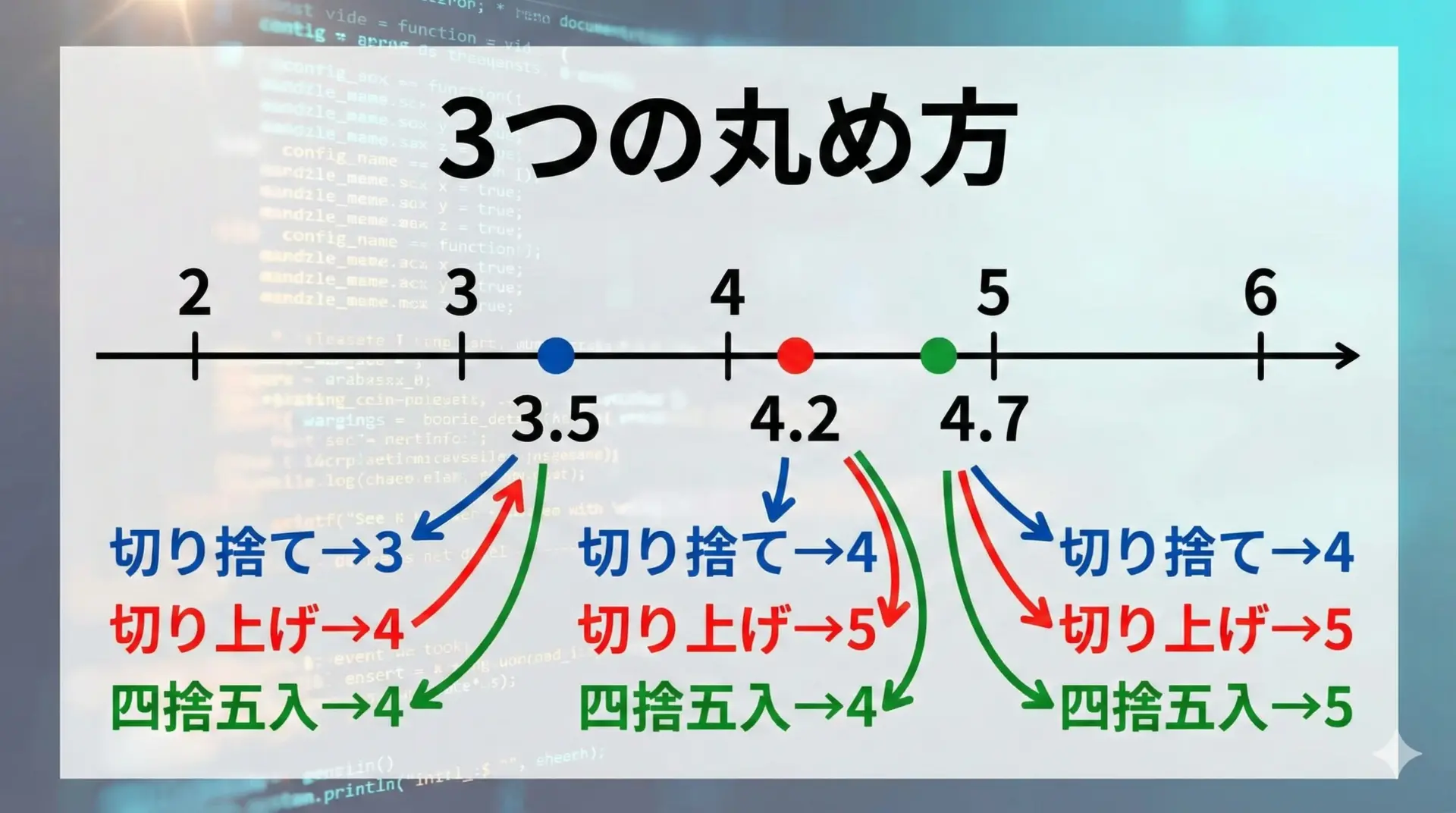
サンプルコードで具体的に見てみます。
#include <stdio.h>
#include <math.h>
int main(void) {
double x = 10.0;
double r = sqrt(x); // 約3.162...
// 1. 切り捨て (整数部分だけを取り出す)
int floor_val = (int)r;
// 2. 切り上げ (ceil関数を利用)
int ceil_val = (int)ceil(r);
// 3. 四捨五入 (0.5を足してから切り捨て)
int round_val = (int)(r + 0.5);
printf("x = %f, sqrt(x) = %f\n", x, r);
printf("floor: %d\n", floor_val);
printf("ceil : %d\n", ceil_val);
printf("round: %d\n", round_val);
return 0;
}x = 10.000000, sqrt(x) = 3.162278
floor: 3
ceil : 4
round: 3この例ではsqrt(10.0)が約3.162…なので、
- 切り捨て → 3
- 切り上げ → 4
- 四捨五入 → 3
となります。
どの丸め方が「正しい」かは用途次第です。
例えば、配列のインデックスに使うなら「切り捨て」、必要な要素数を見積もるなら「切り上げ」、数学的な計算結果を整数で表示するなら「四捨五入」など、目的に応じて選択してください。
sqrtとfabs・powなど関連関数の使い分け
sqrtは数学ライブラリmath.hに含まれる関数の1つであり、fabsやpowなどと組み合わせて使われることが多いです。

代表的な関数と役割の比較を以下に示します。
| 関数 | 役割 | 例 |
|---|---|---|
| sqrt | 平方根(2乗を“戻す”) | sqrt(9.0) = 3.0 |
| fabs | 絶対値 | fabs(-3.5) = 3.5 |
| pow | 累乗(べき乗) | pow(2.0, 3.0) = 8.0 |
| cbrt(C99) | 立方根 | cbrt(8.0) = 2.0 |
| hypot | √(x^2 + y^2)を安全に計算 | hypot(x, y) = sqrt(xx + yy) |
特にpowとsqrtの使い分けはよく話題になります。
sqrt(x)はpow(x, 0.5)とほぼ同じ意味ですが、通常はsqrtの方が高速で精度面でも有利です。- 2乗するなら
pow(x, 2.0)ではなくx * xの方が高速で明快です。
また、距離計算ではsqrt(xx + yy)の代わりにhypot(x, y)を使うと、オーバーフローやアンダーフローに対してより安全な計算が行われます。
C99以降であれば、距離計算にはhypotを優先的に検討すると良いです。
sqrtとエラー処理・移植性
sqrtでのエラー判定方法
sqrtのエラー処理は、Cのバージョンや実装(処理系)によって扱いが異なり、少しややこしいです。
代表的な方法としては、次の2つがあります。
errnoを利用する方法- 結果が
NaNかどうかをisnanで判定する方法
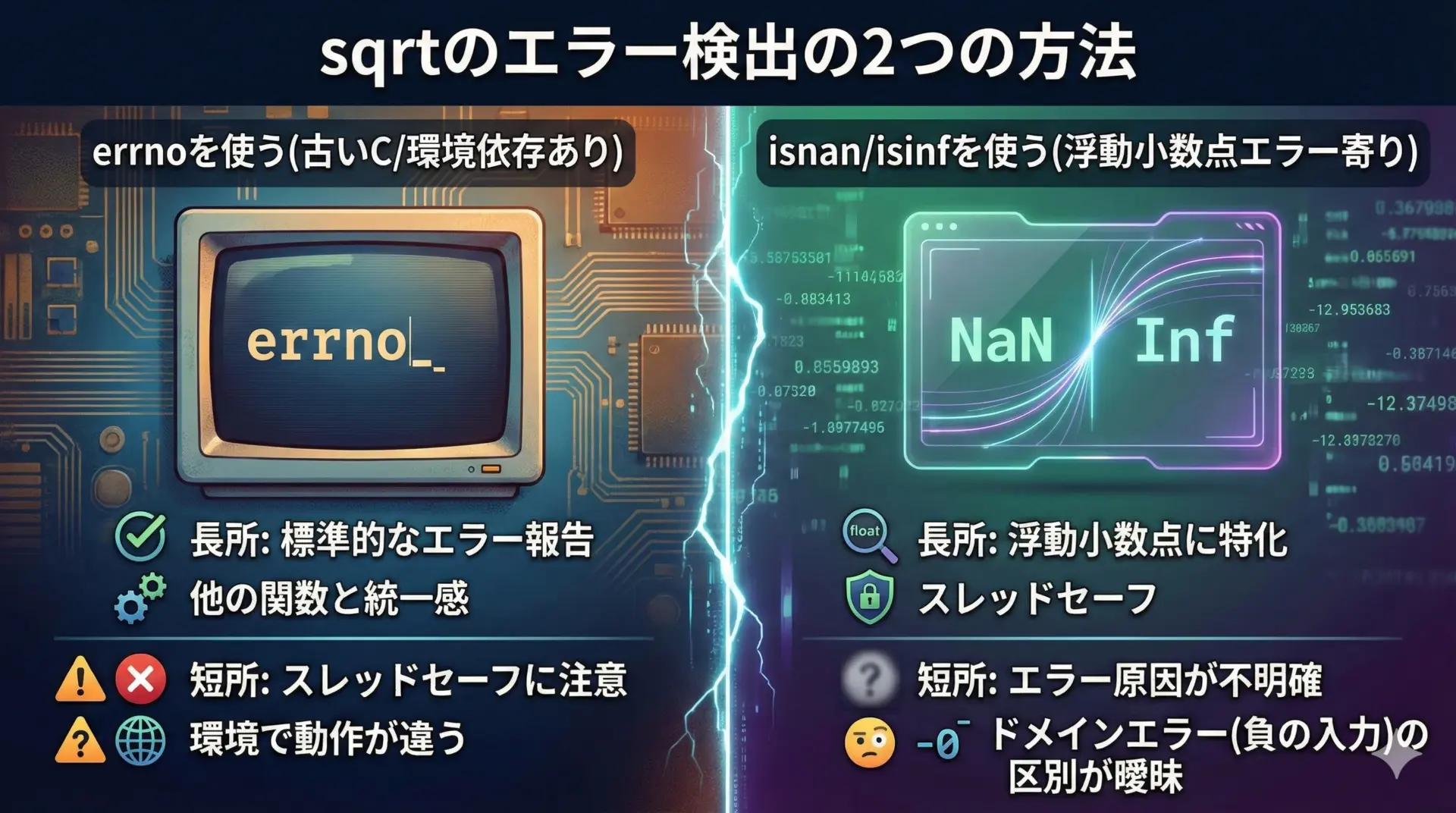
errnoを使ったエラー判定の例を示します。
#include <stdio.h>
#include <math.h>
#include <errno.h>
int main(void) {
double x = -1.0;
errno = 0; // errnoを0で初期化
double r = sqrt(x); // 不正な引数
if (errno == EDOM) { // 領域エラー(domain error)を検出
printf("domain error: x = %f\n", x);
} else {
printf("sqrt(%f) = %f\n", x, r);
}
return 0;
}ここで重要なのは、sqrtを呼ぶ前にerrnoを0に初期化しておくことです。
初期化しておかないと、過去のどこかで発生したエラーが残っている可能性があります。
ただし、errnoにエラーを設定するかどうかは実装依存であり、必ずしもEDOMになるとは限りません。
このため、実務ではisnanやisinfによるチェックも併用することが多いです。
isnan・isinfで結果をチェックする方法
浮動小数点のエラー状態を検出するために、C99以降ではisnanやisinfといったマクロが用意されています。
これらはmath.hに定義されています。
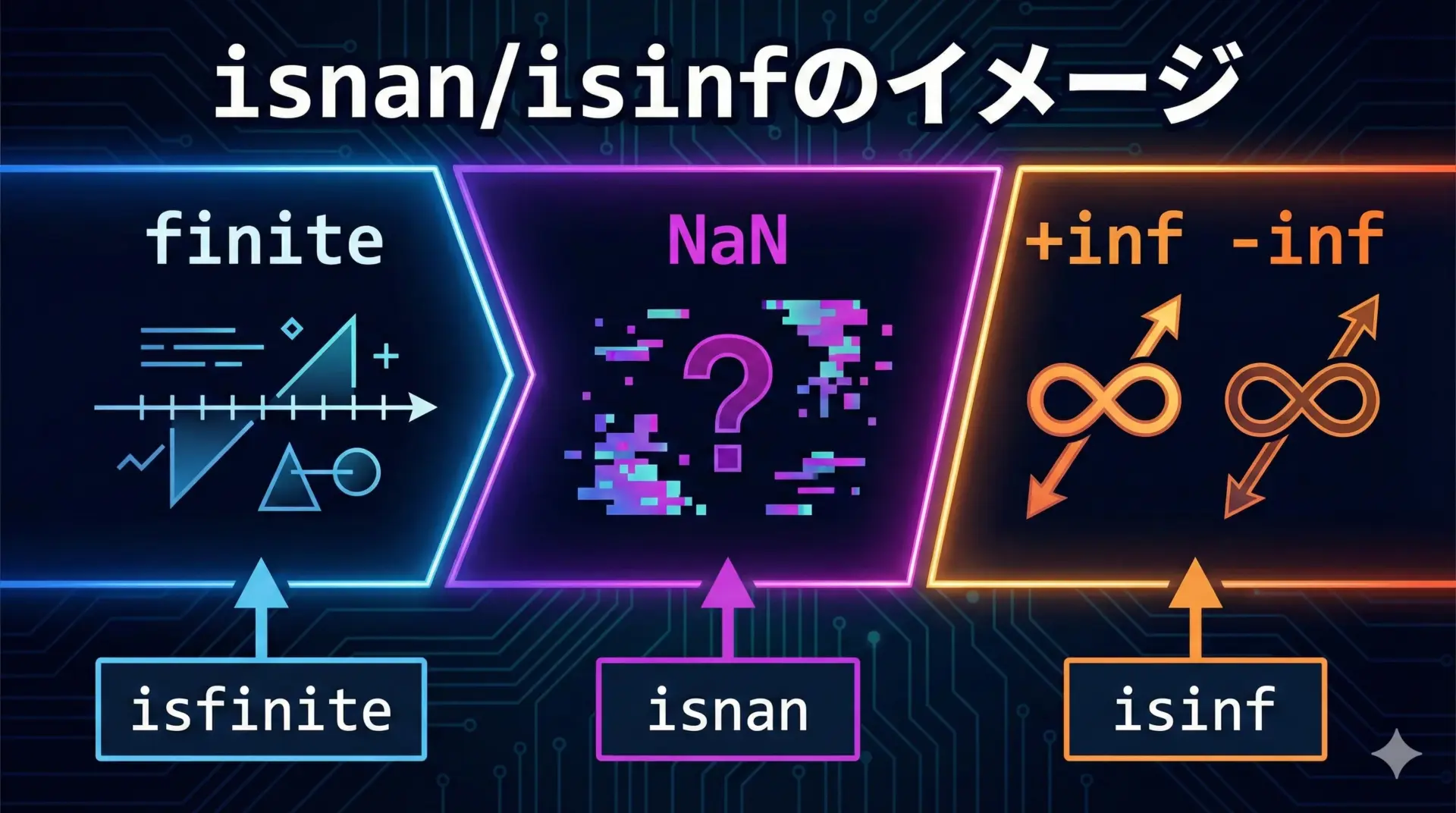
次のコードは、sqrtの結果が正常な数値かどうかをisnanとisinfで判定する例です。
#include <stdio.h>
#include <math.h>
int main(void) {
double x1 = 4.0;
double x2 = -1.0;
double r1 = sqrt(x1);
double r2 = sqrt(x2);
// x1の結果をチェック
if (isnan(r1)) {
printf("sqrt(%f) is NaN\n", x1);
} else if (isinf(r1)) {
printf("sqrt(%f) is infinite\n", x1);
} else {
printf("sqrt(%f) = %f (finite)\n", x1, r1);
}
// x2の結果をチェック
if (isnan(r2)) {
printf("sqrt(%f) is NaN\n", x2);
} else if (isinf(r2)) {
printf("sqrt(%f) is infinite\n", x2);
} else {
printf("sqrt(%f) = %f (finite)\n", x2, r2);
}
return 0;
}sqrt(4.000000) = 2.000000 (finite)
sqrt(-1.000000) is NaN負の引数を与えるとNaNになることが多く、このようにisnanで検出できます。
また、非常に大きな値を渡した場合などにはinfになる可能性もあり、その場合はisinfで検出できます。
C89/C99でのsqrtの扱いと移植性の注意点
Cのバージョンによって、sqrtまわりの仕様には差があります。
古い環境や組み込み環境でコードを動かす場合には、これらの差を意識する必要があります。

代表的な違いを表にまとめます。
| 項目 | C89 | C99以降 |
|---|---|---|
| sqrtの存在 | あり | あり |
| sqrtf/sqrtl | 規格外(実装依存) | 規格で定義済み |
| isnan/isinf | 規格外(実装依存) | 規格で定義済み |
| <tgmath.h> | なし | あり(型に応じてsqrt/sqrtfなどを自動選択) |
| NaN/infの扱い | 実装依存要素が大きい | IEEE 754を前提にした記述が充実 |
このため、「C89互換性が必要なコード」ではsqrtfやsqrtl、isnanなどを使うとコンパイルエラーになる可能性があります。
対策としては次のような方法があります。
- 可能であれば
double sqrt(double)だけを使い、float/long doubleの扱いを限定する - コンパイラや標準ライブラリがC99以降に対応していることを前提にする
- 条件付きコンパイル(
#ifなど)でC89環境向けコードを分岐する
移植性を高めたい場合、「必要最小限の機能だけを使う」「コンパイラの対応状況を明確にする」ことが重要です。
高速な平方根計算が必要な場合の代替手段
sqrtは便利ですが、多量の計算を行う場合やリアルタイム性が求められる場合には、速度がボトルネックになることがあります。
そのような場面では、いくつかの代替手段が検討されます。
近似アルゴリズム(ニュートン法など)
平方根の近似値を求めるには、ニュートン法を使った反復計算が有名です。
精度を多少犠牲にして反復回数を減らすことで、場合によっては標準のsqrtより高速になることもあります(ただし実装やハードウェア次第です)。
以下は、ニュートン法を使って平方根を近似する簡易的な例です。
#include <stdio.h>
// ニュートン法による平方根の近似計算
double fast_sqrt(double x) {
if (x <= 0.0) {
return 0.0; // 単純化のための処理(本来はエラー扱いも検討)
}
double guess = x; // 初期値
// 反復回数を固定回数に制限(ここでは10回)
for (int i = 0; i < 10; i++) {
// ニュートン法の更新式: g_{n+1} = (g_n + x / g_n) / 2
guess = 0.5 * (guess + x / guess);
}
return guess;
}
int main(void) {
double x = 10.0;
double r1 = sqrt(x); // 標準ライブラリのsqrt
double r2 = fast_sqrt(x); // ニュートン法による近似
printf("sqrt(%f) = %.15f\n", x, r1);
printf("fast_sqrt(%f) = %.15f\n", x, r2);
return 0;
}sqrt(10.000000) = 3.162277660168380
fast_sqrt(10.000000) = 3.162277660168379このように、十分な反復回数を取ればかなり良い精度が得られますが、「常に標準のsqrtより速い」とは限らない点に注意してください。
現代のCPUでは、ハードウェア実装された平方根命令が非常に高速なため、安易に自前実装に置き換えると逆に遅くなる場合もあります。
ハードウェア機能や最適化ライブラリの利用
より本格的な高速化が必要な場合は、次のようなアプローチが現実的です。
- SIMD命令(SSE, AVXなど)を利用して複数の平方根を同時に計算する
- GPUでのベクトル計算にオフロードする
- BLASや各種数値計算ライブラリに実装された最適化されたルーチンを利用する
これらは環境依存が強いため、プロジェクトの要件(対応プラットフォーム、性能目標)に応じて選択する必要があります。
一般的なアプリケーションでは、まずは標準のsqrtで実装し、性能が問題になった場合にのみ高速化策を検討するのが現実的な進め方です。
まとめ
sqrtはC言語における平方根計算の基本関数であり、正しく使えば非常に強力な道具です。
一方で、整数との型変換や浮動小数点誤差、負数入力時のNaN・errnoの扱い、C89/C99間の仕様差など、押さえておくべきポイントも多く存在します。
記事を通して、「ヘッダとリンク」「型と丸め」「エラー検出」「関連関数との使い分け」という4つの観点から理解を深めたことで、現場で安心してsqrtを活用できるはずです。
今後は距離計算や統計処理など、実際のアプリケーションコードの中でsqrtを積極的に使いながら、ここで学んだ注意点を体感しつつ身につけていってください。

