Pythonでの数値計算では、ちょっと足し算しただけなのに「0.3」が「0.30000000000000004」と表示されて戸惑った経験はないでしょうか。
この現象はPython特有のものではなく、コンピュータで小数を扱う仕組みによるものです。
本記事では、その正体であるfloatの誤差を丁寧に分解し、decimalモジュールのDecimal型を使って桁ズレや丸め誤差を解消する方法を、実務で使えるレベルまで詳しく解説します。
Pythonのfloat誤差とは何か
Pythonの浮動小数点(float)の仕組み
Pythonのfloatは「実数」ではない
Pythonのfloatは、数学でいう実数をそのまま表しているわけではありません。
多くの環境で、Pythonのfloatは「IEEE 754 倍精度浮動小数点数」という形式で、2進数を使って近似的に表現されています。
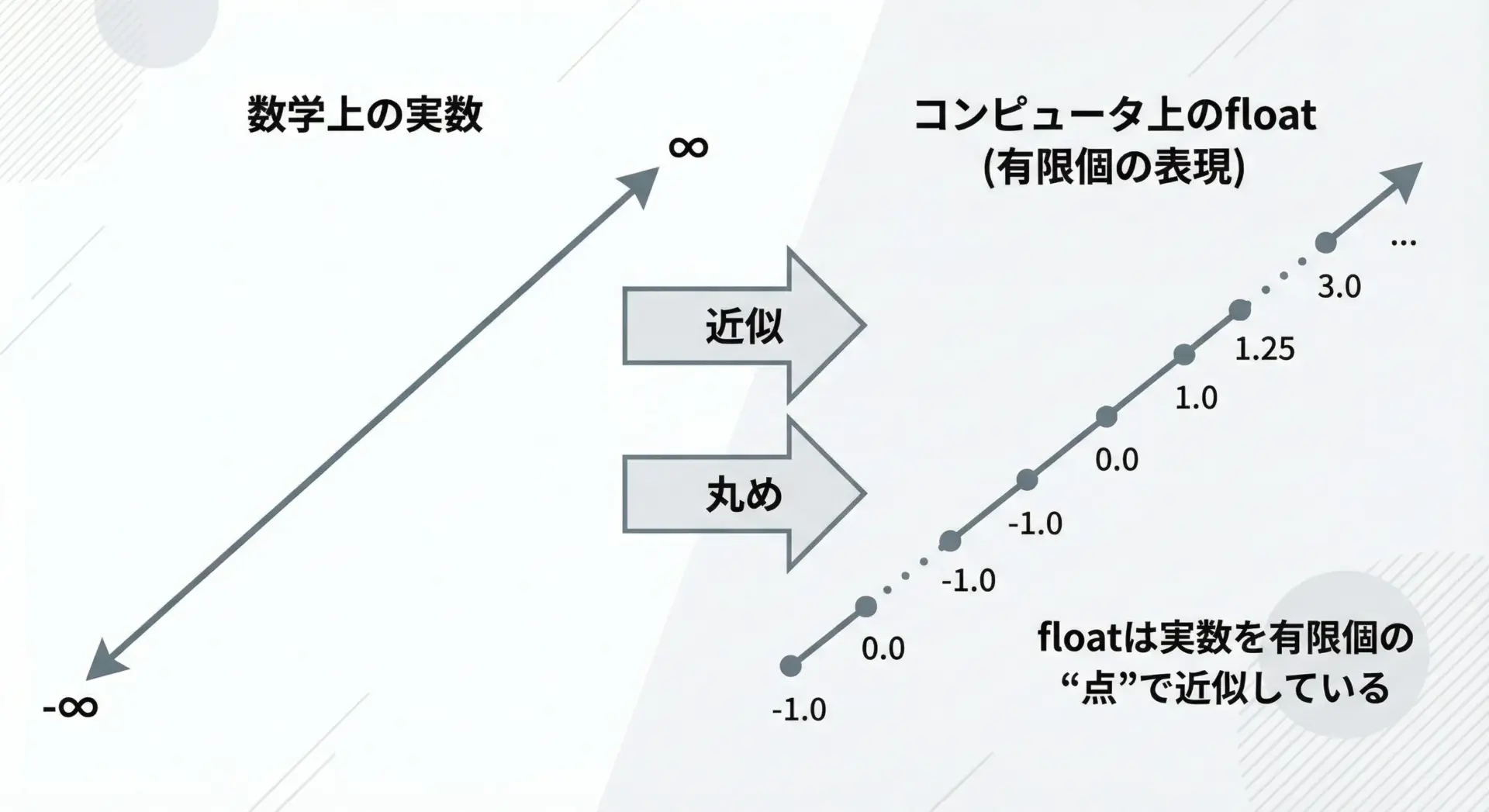
この「近似」というキーワードが重要です。
コンピュータは無限桁の小数を格納できないため、格納可能なビット数に収まるように、できるだけ近い数値に丸めて保存しています。
そのため、見た目は「0.1」と書いていても、内部では「0.1に非常に近いが、ぴったりではない数字」が保存されている場合があります。
IEEE 754 倍精度浮動小数点のざっくり構造
floatは、おおまかに次の3つの部分に分かれています。
- 符号部(sign)
- 指数部(exponent)
- 仮数部(mantissa または significand)

この52ビット分の仮数部が、10進数に直すとおおよそ15〜16桁の精度に相当します。
しかし、この精度は「10進のきれいな桁」が保証されているわけではなく、「2進数として表現できる範囲での精度」です。
この点が、後述する丸め誤差の根本原因となります。
2進数表現による丸め誤差の原因
10進小数の多くは2進小数で有限個に表せない
2進数表現による丸め誤差を理解するには、「1/10は2進数では無限小数になる」という事実が重要です。
10進数では、1/10 = 0.1として有限桁で表せます。
しかし、2進数では次のようになります。
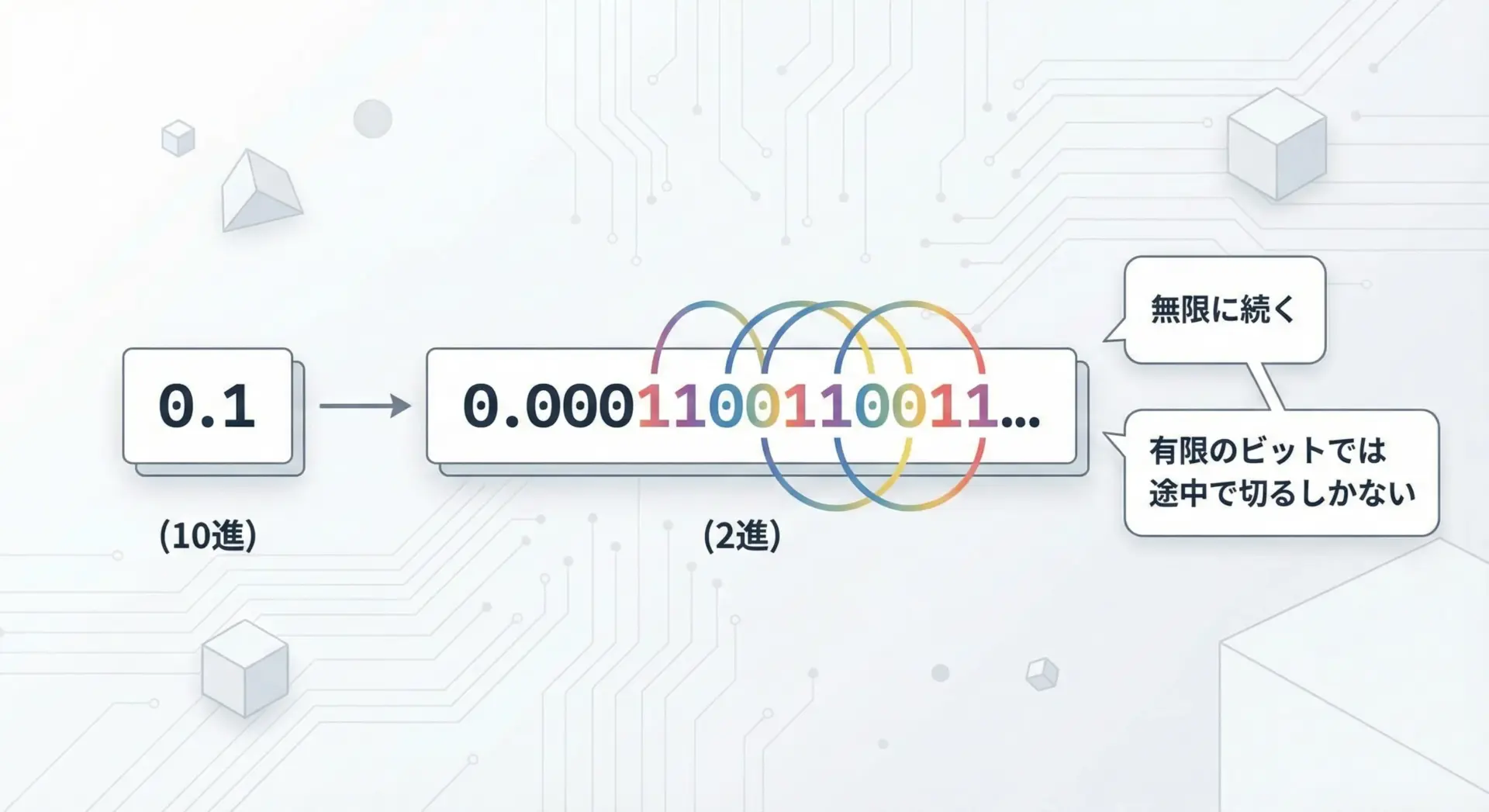
このように、0.1は2進数では循環小数になり、52ビットという有限の仮数部に収めるために途中で切り捨て(または丸め)が発生します。
その結果、コンピュータ内には「0.1に非常に近いが、正確には0.1ではない値」が保存されます。
実際に0.1の内部表現を確認してみる
Pythonでは、Decimalやformat関数を使って、この「わずかなズレ」を確認できます。
from decimal import Decimal
# floatの0.1をそのままDecimalに変換してみる
f = 0.1
d_from_float = Decimal(f) # float経由でDecimalに変換
d_from_str = Decimal("0.1") # 文字列からDecimalに変換(正確)
print("floatそのもの:", f)
print("float→Decimal:", d_from_float)
print("文字列→Decimal:", d_from_str)
print("差分(Decimal):", d_from_float - d_from_str)floatそのもの: 0.1
float→Decimal: 0.1000000000000000055511151231257827021181583404541015625
文字列→Decimal: 0.1
差分(Decimal): 5.551115123125782702118158340E-18出力を見て分かるように、内部的には0.1よりわずかに大きい値として表現されています。
人間にはほぼ0.1に見えますが、コンピュータにとっては「別の数字」です。
floatで起こる典型的な誤差例
0.1 + 0.2 が 0.3 にならない
もっとも有名な例として、次のコードが挙げられます。
a = 0.1
b = 0.2
c = a + b
print("a + b =", c)
print("a + b == 0.3 ?", c == 0.3)a + b = 0.30000000000000004
a + b == 0.3 ? False人間の感覚では明らかに0.1 + 0.2 = 0.3ですが、floatでは「0.30000000000000004」と表示され、0.3との比較はFalseになってしまいます。
これは、0.1も0.2も内部的にはそれぞれ「近似値」であるため、それらを足した結果もまた、0.3からわずかにズレた近似値になるからです。
繰り返し加算による累積誤差
丸め誤差は一度だけなら目立ちませんが、何度も繰り返すことで累積誤差として顕在化します。
x = 0.1
total = 0.0
for _ in range(10):
total += x
print("0.1を10回足した結果:", total)
print("total == 1.0 ?", total == 1.0)0.1を10回足した結果: 0.9999999999999999
total == 1.0 ? Falseこのように、理論上は1.0になるはずの計算が、実際には1.0よりわずかに小さくなってしまうことがあります。
統計処理や金融計算などで繰り返し加算を行う場合、この差が大きな問題になることがあります。
float誤差が問題になるケース
金額計算や請求システムでのfloat誤差
請求額が1円ズレる「小さなバグ」が大問題になる
金額計算では、1円の誤差でも重大な問題になります。
例えば、1件あたり数十円の手数料を何万件も積み上げるような決済システムでfloatを使うと、合計額が本来より1円多くなったり少なくなったりすることがあります。
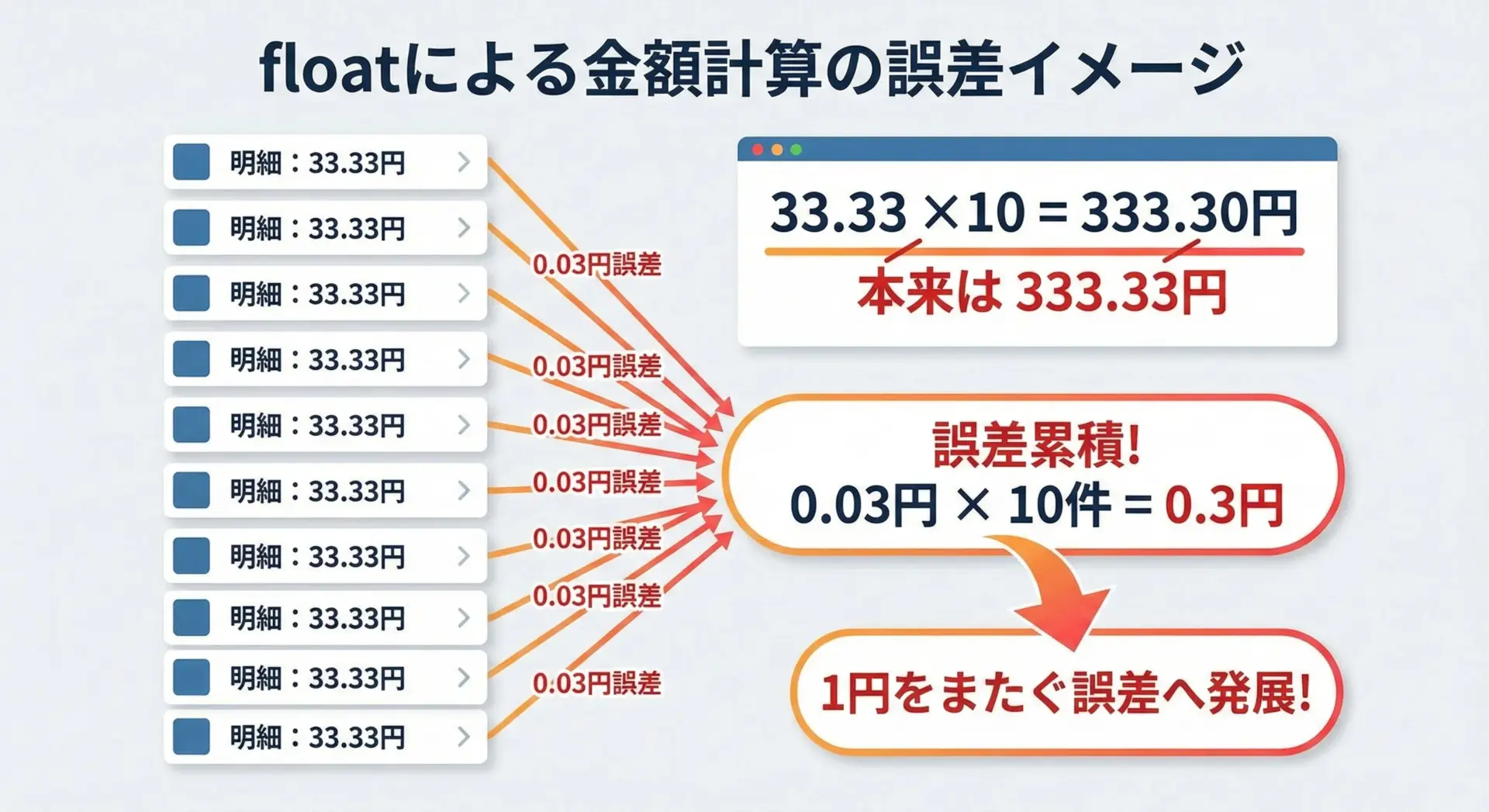
請求処理では、切り上げ/切り捨てや四捨五入のルールも厳密に定められていることが多く、「どのタイミングで小数点以下を処理するか」が法律や契約で決まっていることもあります。
floatではこのルールを厳格に守ることが難しく、Decimalのような10進小数向けの型が求められます。
集計・統計処理での桁ズレ例
大量データの集計で「合計が会計システムと合わない」
BIツールやデータ分析のスクリプトでfloatを使って集計すると、会計システムの数字と合計値が微妙にズレることがあります。
たとえば、カード明細1件ごとに税額を計算し、合計税額を求めたところ、元システムの合計と1円単位で一致しない……といった事例です。
このズレの原因は、大きく2つに分けられます。
- 各行の金額や税額をfloatで保持していることによる丸め誤差
- 各行で丸めを行った結果と、合計後に丸めを行った結果の違い
前者は今回のテーマであるfloat誤差そのものですが、後者も金額計算では頻出の罠です。
どちらも、Decimalを使い、かつ「どのステップで丸めるか」の設計を明示することで回避しやすくなります。
比較演算(==)での思わぬバグ
「等しいはずなのにFalseになる」典型パターン
floatは近似値であるため、直接==で比較するのは基本的に危険です。
次の例を見てください。
x = 0.1 * 3
y = 0.3
print("x:", x)
print("y:", y)
print("x == y ?", x == y)x: 0.30000000000000004
y: 0.3
x == y ? False同じ計算のはずなのにFalseになるため、「条件分岐に入らない」「ループが終わらない」などのバグを引き起こします。
本来は次のように、許容誤差(イプシロン)を用いた比較を行うべきです。
x = 0.1 * 3
y = 0.3
eps = 1e-9 # 許容誤差
is_equal = abs(x - y) < eps
print("x ≒ y ?", is_equal)x ≒ y ? Trueしかし、金額計算などでは「おおよそ等しい」ではなく、「1円単位で完全に一致している」ことが重要です。
そのような用途では、float自体を避けてDecimalを使うほうが安全です。
Decimalでfloat誤差を解消する方法
decimalモジュールの基本
Decimalは「10進小数のための型」
Python標準ライブラリのdecimalモジュールは、10進小数を正確に扱うためのDecimal型を提供します。
floatが2進数を基盤としているのに対し、Decimalは10進数を基盤としており、0.1や0.01といった日常的な小数を誤差なく表現できます。
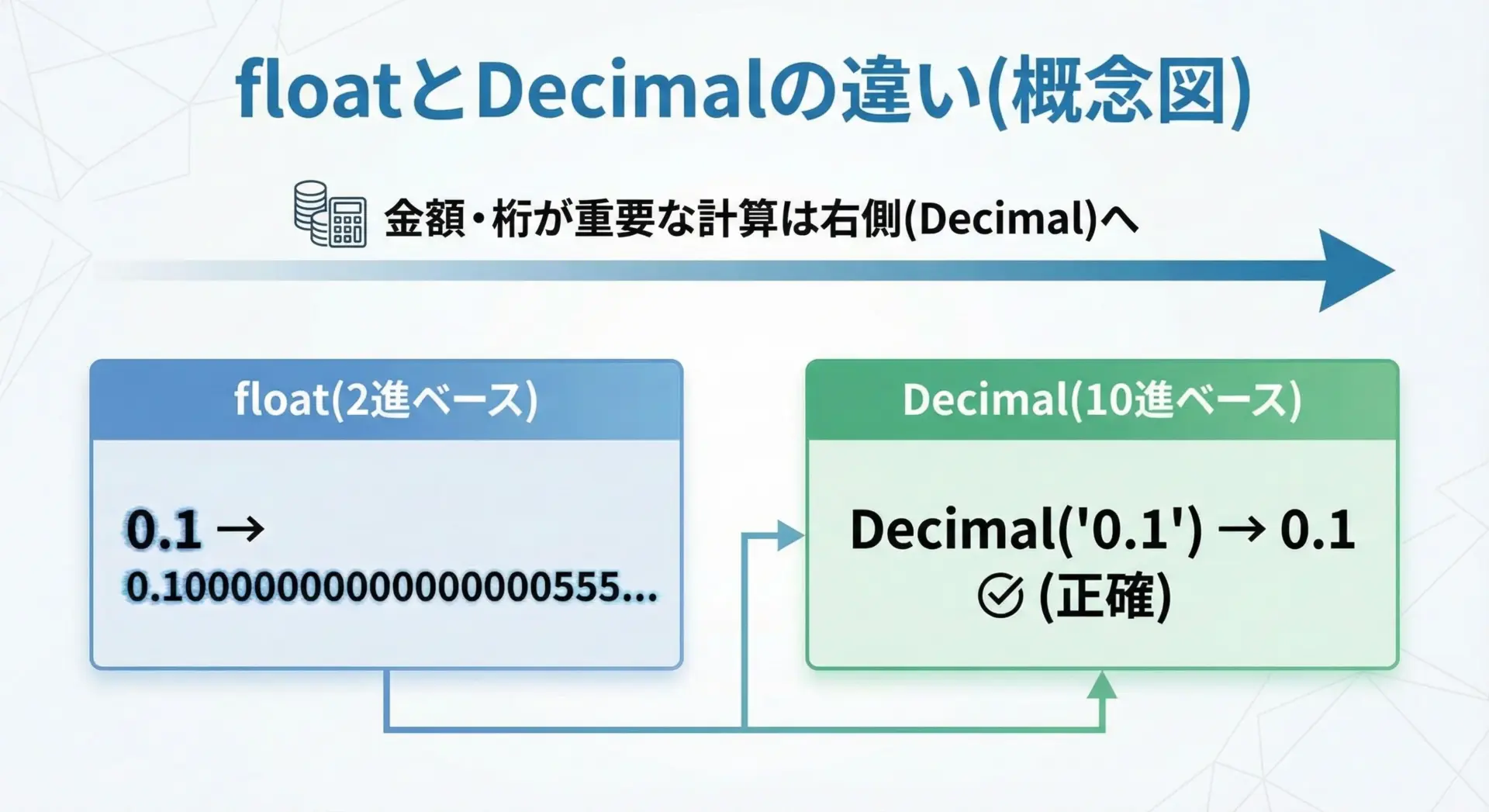
Decimalは次のような特徴を持ちます。
- 10進表記の値を正確に表現できる
- 計算結果も10進のルールに従って丸められる
- コンテキスト(精度や丸めモード)を柔軟に設定できる
- 金融・会計で求められる厳密な桁管理に向いている
Decimalの使い方
基本的な生成と演算
Decimalを使うには、まずdecimalモジュールをインポートして、Decimalクラスを利用します。
from decimal import Decimal
# 文字列からDecimalを生成(推奨)
a = Decimal("0.1")
b = Decimal("0.2")
c = a + b
d = a * b
print("a + b =", c)
print("a * b =", d)a + b = 0.3
a * b = 0.02floatの場合と違い、0.1 + 0.2 が正しく 0.3 になります。
ここで重要なのは、文字列からDecimalを生成している点です。
この理由は後述します。
Decimalとfloatを混在させない
Decimalとfloatを混在させると、Decimal側にfloatの誤差が持ち込まれてしまいます。
from decimal import Decimal
a = Decimal("0.1")
b = 0.2 # float
# 混在計算
c = a + b
print("a + b =", c)
print("型:", type(c))a + b = 0.3000000000000000166533453694
型: <class 'decimal.Decimal'>見た目はDecimalですが、誤差を含んだ値になっています。
原因は、「0.2」がすでにfloatの誤差を含んだ近似値であり、それをDecimalに巻き込んでいるからです。
このような事態を避けるためには、一貫してDecimalのみを使うことが重要です。
floatからDecimalへ安全に変換するコツ
文字列経由で変換する
floatからDecimalに変換する際のポイントは、float値そのものではなく「文字列表現」から変換することです。
from decimal import Decimal
f = 0.1
# 悪い例: floatを直接渡す
d_bad = Decimal(f)
# 良い例: 文字列を渡す
d_good = Decimal("0.1")
print("bad:", d_bad)
print("good:", d_good)
print("差分:", d_bad - d_good)bad: 0.1000000000000000055511151231257827021181583404541015625
good: 0.1
差分: 5.551115123125782702118158340E-18この差からも分かるように、float → Decimal の直接変換は、floatの誤差をそのままDecimalに持ち込むため、金額計算のような用途では避けるべきです。
可能であれば、最初から文字列として値を受け取り、その文字列をDecimalに変換する設計にしましょう。
外部データの読み込み時の工夫
CSVやDBから数値を読み込む場合、次のような方針が安全です。
- 金額カラムは文字列のまま取得し、Decimalに変換する
- すでにfloatとして入っている場合も、
formatなどで文字列化した上でDecimalに変換する
from decimal import Decimal
f = 0.1 # どうしてもfloatで渡されてしまうケース
d_safer = Decimal(format(f, ".10g")) # 適切な桁数で文字列化してからDecimalへ
print("元のfloat:", f)
print("変換後Decimal:", d_safer)元のfloat: 0.1
変換後Decimal: 0.1format時の桁数(.10gなど)は、扱うドメインや必要精度に応じて調整します。
コンテキスト設定(precisionと丸めモード)のポイント
getcontextでグローバル設定を行う
Decimalはgetcontext()を使って、精度(precision)や丸めモード(rounding)を設定できます。
from decimal import Decimal, getcontext
# コンテキストを取得
ctx = getcontext()
# 精度を28桁に設定(デフォルトもだいたい28)
ctx.prec = 28
# 丸めモードを「四捨五入(ROUND_HALF_UP)」に設定
ctx.rounding = "ROUND_HALF_UP"
a = Decimal("1") / Decimal("7")
print("1/7 =", a)
print("有効桁数:", ctx.prec)
print("丸めモード:", ctx.rounding)1/7 = 0.1428571428571428571428571429
有効桁数: 28
丸めモード: ROUND_HALF_UP精度(prec)は「計算全体での有効桁数」を表し、金額計算では「整数部の桁数 + 小数部の桁数」程度をカバーできるように設定します。
例えば「最大999兆9999億…円まで扱うが、小数は2桁(銭)まで」といった要件に応じて決めます。
ローカルな一時コンテキストを使う
全体設定を変えたくない場合は、localcontextを使って、一時的にコンテキストを変更できます。
from decimal import Decimal, getcontext, localcontext
x = Decimal("1") / Decimal("3")
print("デフォルト精度:", getcontext().prec, "=>", x)
with localcontext() as ctx:
ctx.prec = 5
y = Decimal("1") / Decimal("3")
print("一時精度5桁 :", y)
print("元の精度に戻る :", Decimal("1") / Decimal("3"))デフォルト精度: 28 => 0.3333333333333333333333333333
一時精度5桁 : 0.33333
元の精度に戻る : 0.3333333333333333333333333333金融系などで「この処理ブロックだけ精度や丸めルールを変えたい」といったケースでも、安全に扱うことができます。
金額計算をDecimalで正確に行うサンプルコード
サンプル: 税込金額の計算と合計
ここでは、次のような要件を想定したサンプルを示します。
- 単価、数量から小計を計算する
- 税率10%をかけて税込金額を求める
- 1明細ごとに税込金額を1円未満四捨五入する(ROUND_HALF_UP)
- 最後に合計金額を出す
from decimal import Decimal, getcontext, ROUND_HALF_UP
# グローバルコンテキストの設定
ctx = getcontext()
ctx.prec = 28 # 金額計算に十分な精度
ctx.rounding = ROUND_HALF_UP # 四捨五入
# 単価・数量・税率は文字列からDecimalに変換
items = [
{"name": "商品A", "price": Decimal("1980"), "qty": Decimal("2")},
{"name": "商品B", "price": Decimal("550"), "qty": Decimal("3")},
{"name": "商品C", "price": Decimal("99.9"), "qty": Decimal("10")},
]
tax_rate = Decimal("0.10") # 10%
grand_total = Decimal("0")
for item in items:
# 小計(税抜)
subtotal = item["price"] * item["qty"]
# 税額
tax = subtotal * tax_rate
# 税込金額を1円未満四捨五入
total_with_tax = (subtotal + tax).quantize(Decimal("1")) # 小数部0桁へ丸め
grand_total += total_with_tax
print(f"{item['name']}: 単価 {item['price']} 円 × {item['qty']} 個")
print(f" 小計(税抜): {subtotal} 円")
print(f" 税額 : {tax} 円")
print(f" 税込金額 : {total_with_tax} 円")
print("-" * 30)
print("合計(税込):", grand_total, "円")商品A: 単価 1980 円 × 2 個
小計(税抜): 3960 円
税額 : 396.0 円
税込金額 : 4356 円
------------------------------
商品B: 単価 550 円 × 3 個
小計(税抜): 1650 円
税額 : 165.0 円
税込金額 : 1815 円
------------------------------
商品C: 単価 99.9 円 × 10 個
小計(税抜): 999.0 円
税額 : 99.90 円
税込金額 : 1099 円
------------------------------
合計(税込): 7269 円このサンプルでは、次の点がポイントです。
- 単価・数量・税率をすべて文字列からDecimalに変換している
- コンテキストの丸めモードを
ROUND_HALF_UPに設定し、日本の一般的な「四捨五入」に合わせている quantize(Decimal("1"))で1円未満を四捨五入し、金額の丸めルールを明示している
floatで同じ処理を行うと、どこかで1円ずれる可能性があるのに対し、Decimalを用いることで桁の整合性を保ちやすくなります。
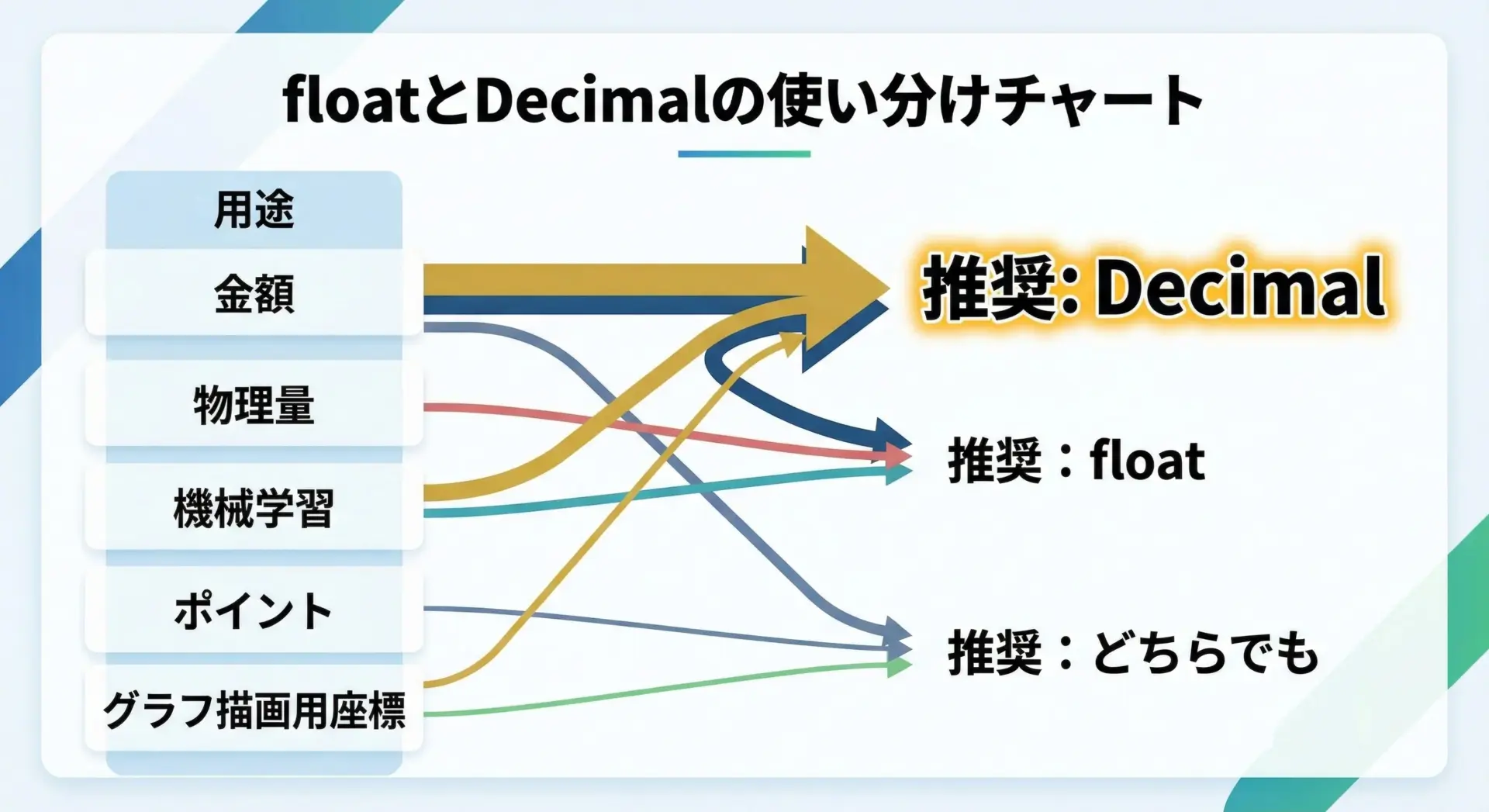
floatとDecimalを使い分ける指針
floatを使ってよい場面
科学技術計算や機械学習など「近似」が前提の分野
floatは高速でメモリ効率もよく、多くの数値計算ライブラリの前提型になっています。
次のような場面では、むしろfloatを使うのが自然です。
- 機械学習(ニューラルネットワークの重みなど)
- 物理シミュレーション
- 画像処理、音声処理
- 統計解析(ただし最終的なレポート値は丸めルールに注意)
これらの分野では、数値自体がもともと観測誤差やモデル誤差を含むため、floatの丸め誤差は支配的な誤差ではありません。
そのため、「誤差を限りなくゼロにする」よりも、「高速に大量の計算をこなす」ことが重視されます。
UI上の簡易表示や内部ロジックの一時値
また、金額であっても次のようなケースではfloatで済ませることがあります。
- 内部ロジックの一時的な演算で、最終的にはDecimalに詰め替える場合
- 概算表示やプログレス表示など、1円レベルの厳密性が不要なUI
とはいえ、一度でもfloatにした値を、そのまま「正確な金額」として扱うのは避けるべきです。
Decimalを使うべき場面
金額・通貨・ポイントなど「桁」が意味を持つもの
次のような情報は、Decimal一択と考えたほうが安全です。
- 金額(売上、請求額、残高、税額など)
- 通貨換算レート(特にレポートレベルでの金額)
- ポイントやマイルなど、整数や固定小数点で扱うべき値
- 割引率や手数料率など、金額に直接かかる割合
また、契約や規約で「小数第3位を四捨五入する」「1円未満は切り捨てる」といったルールが明示されている場合、それをプログラムで「検証可能な形で」実装するには、Decimalのquantizeや丸めモードが非常に役立ちます。
既存コードのfloat誤差をDecimalで改善する手順
移行のステップを分解して考える
すでにfloatで実装されているシステムをDecimalに移行する場合、いきなり全体を置き換えるとバグを生みやすくなります。
次のようなステップで、徐々に安全に移行することをおすすめします。
- 金額やレートなど「ビジネス的に重要な値」がどこで使われているか洗い出す
- その値の入力経路(外部API、DB、UIなど)を調査し、可能なら文字列で受け取るよう変更
- 内部表現をDecimalに変更し、計算部分もDecimal専用に書き換える
- 丸めルール(四捨五入・切り捨て・切り上げ)を仕様と照合し、
quantizeで明示的に指定 - 結果のフォーマット(表示・外部送信)をDecimal対応にする
- 既存のテストケースをDecimal版に対して実行し、結果が期待値と一致するか検証
部分的な書き換え例
簡単な例として、「floatで金額を扱っていた関数」をDecimal対応に書き換える流れを示します。
# 既存: floatで税込金額を計算する関数(誤差リスクあり)
def calc_total_price_float(price, qty, tax_rate):
"""
price: 税抜単価(float)
qty: 数量(floatまたはint)
tax_rate: 税率(float, 例: 0.1)
"""
subtotal = price * qty
tax = subtotal * tax_rate
total = subtotal + tax
# 小数第1位で四捨五入して整数に
return int(round(total))# 改善版: Decimalで税込金額を計算する関数
from decimal import Decimal, ROUND_HALF_UP
def calc_total_price_decimal(price_str, qty_str, tax_rate_str):
"""
price_str: 税抜単価を表す文字列(例: "1980" や "99.9")
qty_str: 数量を表す文字列(例: "3")
tax_rate_str: 税率を表す文字列(例: "0.1")
"""
price = Decimal(price_str)
qty = Decimal(qty_str)
tax_rate = Decimal(tax_rate_str)
subtotal = price * qty
tax = subtotal * tax_rate
total = subtotal + tax
# 1円未満を四捨五入して整数に
total_rounded = total.quantize(Decimal("1"), rounding=ROUND_HALF_UP)
return total_rounded# 使い方の例
print(calc_total_price_decimal("99.9", "10", "0.1"))1099このように、引数の型定義(文字列)から見直すことで、float誤差を完全に排除した設計に近づけることができます。
段階的に関数単位で置き換え、テストで検証しながら進めるのが現実的です。
まとめ
floatの誤差はPython特有のバグではなく、コンピュータが2進数で小数を表現する仕組みに起因する必然的な近似誤差です。
そのため、0.1や0.3といったごく身近な数値であっても、内部的にはわずかにズレた値として扱われ、繰り返し計算や比較演算の場面で思わぬバグを引き起こします。
一方で、標準ライブラリのdecimalモジュールが提供するDecimalを使えば、10進小数を正確に表現でき、金額計算や請求システムなどで求められる厳密な桁管理と丸めルールを実装できます。
重要なのは、どの場面でfloatを使い、どの場面でDecimalを使うべきかを意識的に選択することと、Decimalを利用する際には文字列からの変換と一貫した丸め戦略を徹底することです。
この記事の解説とサンプルコードをベースに、自身のプロジェクトでもfloat誤差をコントロールし、安心して数値計算が行える設計へと改善してみてください。

