Pythonでデータを検索するとき、最初に使うのがin演算子だと思います。
しかし、リスト・辞書・セットのどれに対してinを使うかで、処理速度は大きく変わります。
本記事では、Pythonのin演算子が内部でどのように動き、リスト・辞書・セットで計算量がどう違うのかを、図解とサンプルコードを交えながら詳しく解説します。
Pythonのin演算子とは
in演算子の基本的な使い方
まず、Pythonのin演算子がどのような場面で使われるのかを整理します。
in演算子は、ある値がコンテナ(リストや辞書など)の中に含まれているかどうかを判定するための演算子です。
代表的な使い方は次のようになります。
# リストに対する in 演算子
numbers = [1, 2, 3, 4, 5]
print(3 in numbers) # True
print(10 in numbers) # False
# 文字列に対する in 演算子
text = "hello python"
print("py" in text) # True
print("java" in text) # False
# 辞書に対する in 演算子(キーの検索)
user = {"name": "Alice", "age": 30}
print("name" in user) # True
print("Alice" in user) # False (値ではなくキーを見る点に注意)
# セットに対する in 演算子
fruits = {"apple", "banana", "orange"}
print("apple" in fruits) # True
print("grape" in fruits) # Falseこのように、同じinという書き方でも、対象のデータ構造によって内部の処理が大きく変わります。
そのため、処理速度や計算量もデータ構造ごとに異なります。
in演算子が返す結果
in演算子は、常にTrueかFalseのbool型を返します。
条件分岐やループの継続条件として使う場面が多く、次のようなコードに頻出します。
allowed_users = {"alice", "bob", "charlie"}
user_name = "bob"
if user_name in allowed_users:
print("アクセスを許可します")
else:
print("アクセスを拒否します")このような判定処理が頻繁に、かつ大量のデータに対して行われる場合、in演算子の速度がそのままアプリケーション全体のパフォーマンスに直結します。
メンバーシップ判定と計算量の関係
in演算子は、しばしばメンバーシップ判定(membership test)と呼ばれます。
これは、ある要素が集合の「メンバー」であるかどうかを確認する操作です。
ここで重要なのが計算量の考え方です。
計算量とは、データ量が増えたときに、処理時間がどの程度増えるかをおおまかに表した指標です。
Pythonのin演算子の速度を理解するためには、この計算量を知っておく必要があります。
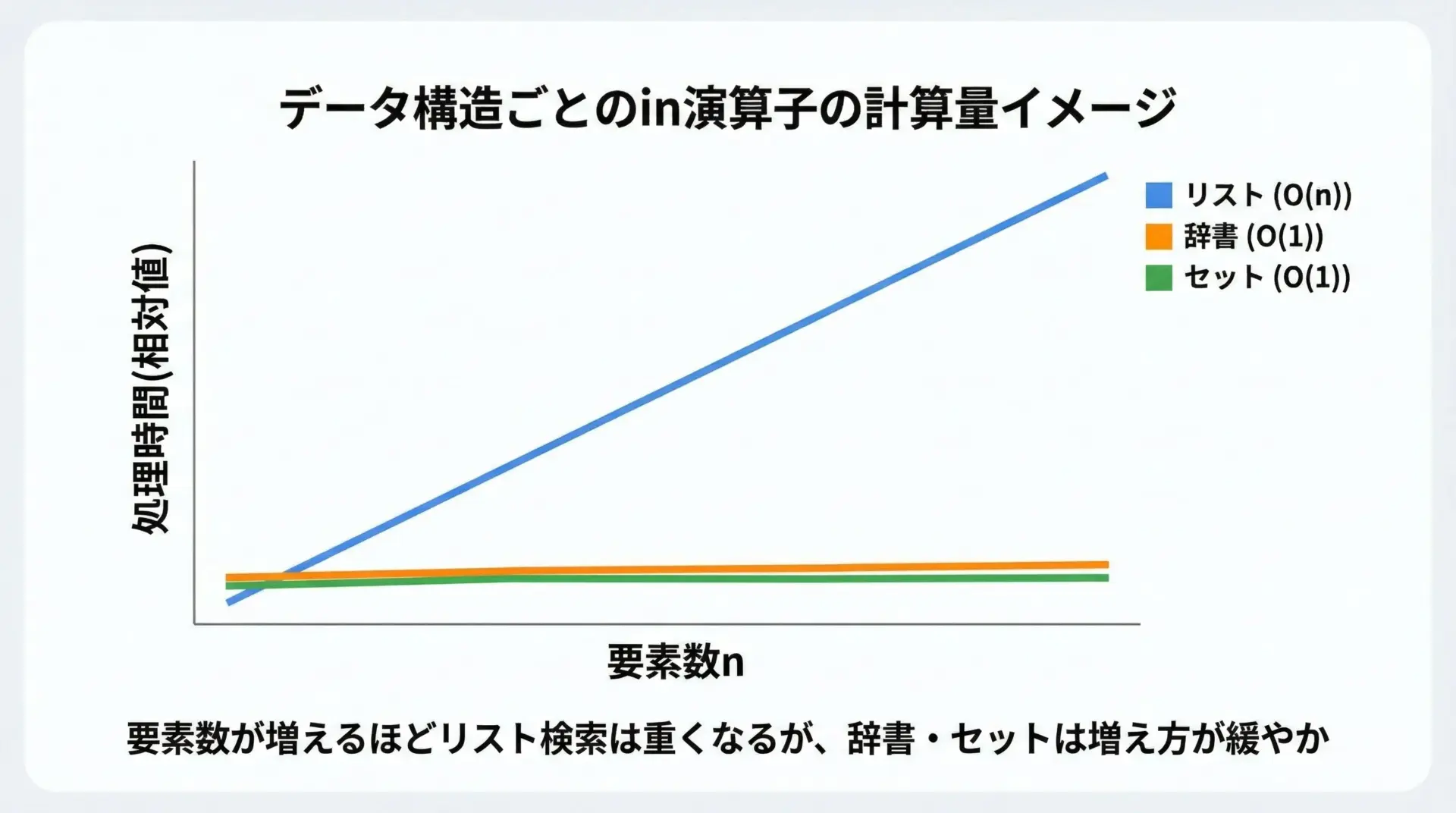
この図のように、リスト・辞書・セットでinの計算量は大きく違います。
一般的には次のように整理できます。
| データ構造 | in演算子が調べる対象 | 平均的な計算量 |
|---|---|---|
| リスト(list) | すべての要素を先頭から順番に比較 | O(n) |
| 辞書(dict) | キーをハッシュテーブルで検索 | O(1) |
| セット(set) | 要素をハッシュテーブルで検索 | O(1) |
同じinでも、リストは線形時間、辞書・セットは平均すると定数時間で検索できます。
この違いが、実行速度に大きな差を生みます。
リスト(list)とin演算子の計算量
リストのin演算子は線形探索(O(n))
リストに対するinは線形探索(linear search)です。
これは、先頭から1つずつ要素を比較していき、一致したら終了するというシンプルな方式です。
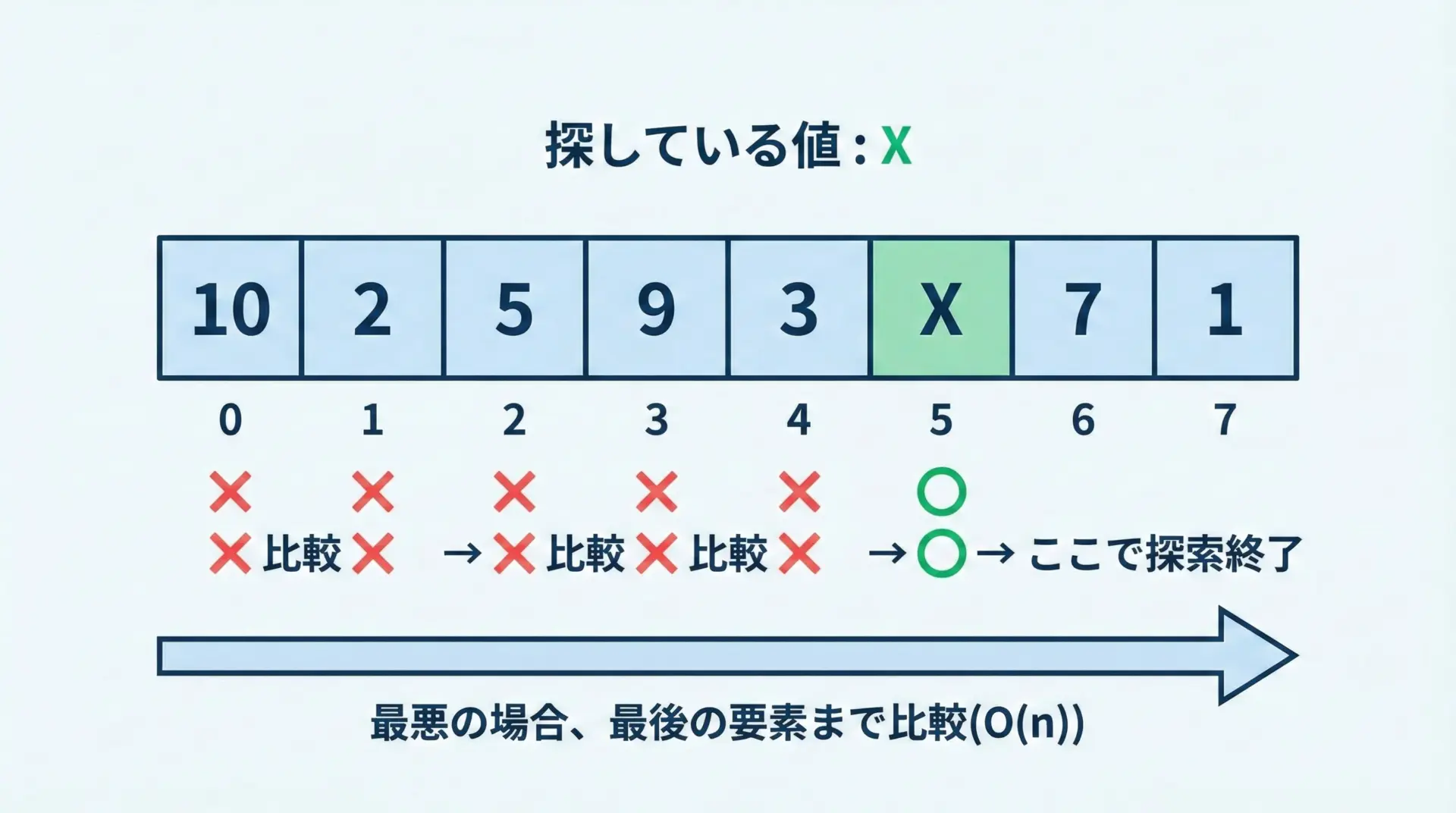
Pythonの実装イメージを擬似コードで表すと、次のような処理をしています。
def contains_in_list(lst, target):
# 実際のCPythonのソースとは異なりますが、
# 挙動のイメージを示す擬似コードです。
for item in lst:
if item == target:
return True
return Falseこの処理の特徴は、最悪の場合、すべての要素を1回ずつ比較する必要があるという点です。
そのため、リストの長さをnとすると、計算量はO(n)となります。
実際にリストの長さによる時間の違いを測る
あくまでイメージですが、簡単なコードでリストサイズと実行時間の関係を計測してみます。
import time
def measure_list_in(n, trials=100):
data = list(range(n))
target = -1 # リストに存在しない値(最悪ケース)
start = time.perf_counter()
for _ in range(trials):
_ = target in data
end = time.perf_counter()
return end - start
sizes = [10, 100, 1_000, 10_000, 100_000]
for size in sizes:
elapsed = measure_list_in(size)
print(f"要素数 {size:>7}: {elapsed:.6f} 秒")上のコードでは、targetが存在しない値になっているため、毎回リスト全体を最後まで走査する最悪ケースの時間を測定しています。
実行環境によって数値は異なりますが、要素数が10倍になると、処理時間もおおよそ10倍程度増える傾向が見られます。
リスト検索が遅くなりやすいケース
リストに対するinが特に遅くなりやすいのは、次のようなケースです。
1つ目は、要素数が非常に多いリストを何度も検索する場合です。
たとえば、ログのIPアドレスリストからブラックリストIPを探す処理を、数万回以上繰り返すような状況です。
2つ目は、探したい要素がリストの末尾付近か存在しない場合です。
線形探索では、見つかるまで前から順に比較していくため、末尾にあるほど比較回数が増えます。
存在しない値の場合は、必ず全要素を確認することになります。
3つ目は、比較コストが高いオブジェクト同士を大量に比較する場合です。
例えば、大きな文字列や複雑なオブジェクトを要素に持つリストでinを行うと、1回あたりの比較が重いため、総時間もさらに増加します。
リストでinを使うべきケース
とはいえ、常にリストが悪い選択肢というわけではありません。
次のようなケースでは、リスト+inで十分か、むしろ適切な場合も多いです。
1つは、要素数が小さい場合(数十〜数百件程度)です。
要素数が少なければ、線形探索でも実行時間はほとんど気になりません。
むしろ、データ構造変換のオーバーヘッドを考えると、シンプルなリストで完結させた方がコードも分かりやすくなります。
もう1つは、要素の順序が重要で、かつ頻繁に並び替えやスライスを行う場合です。
リストは順序付きシーケンスとしての操作に優れており、検索専用ではない多目的なコンテナとして適しています。
そのような場面では、多少inが遅くても、トータルではリストを使うメリットが勝つことがあります。
辞書(dict)とセット(set)のin演算子の計算量
辞書のinはキー検索で平均O(1)
辞書(dict)に対するinは、キーの存在判定を行います。
inは値ではなくキーを見ている点に注意が必要です。
user = {"name": "Alice", "age": 30}
print("name" in user) # True (キーの存在チェック)
print("age" in user) # True (キー)
print("Alice" in user) # False (値は対象外)辞書の内部実装はハッシュテーブル(hash table)であり、平均するとO(1)の計算量でキー検索が可能です。
つまり、データ数が増えても、1回の検索にかかる時間はほとんど増えません。
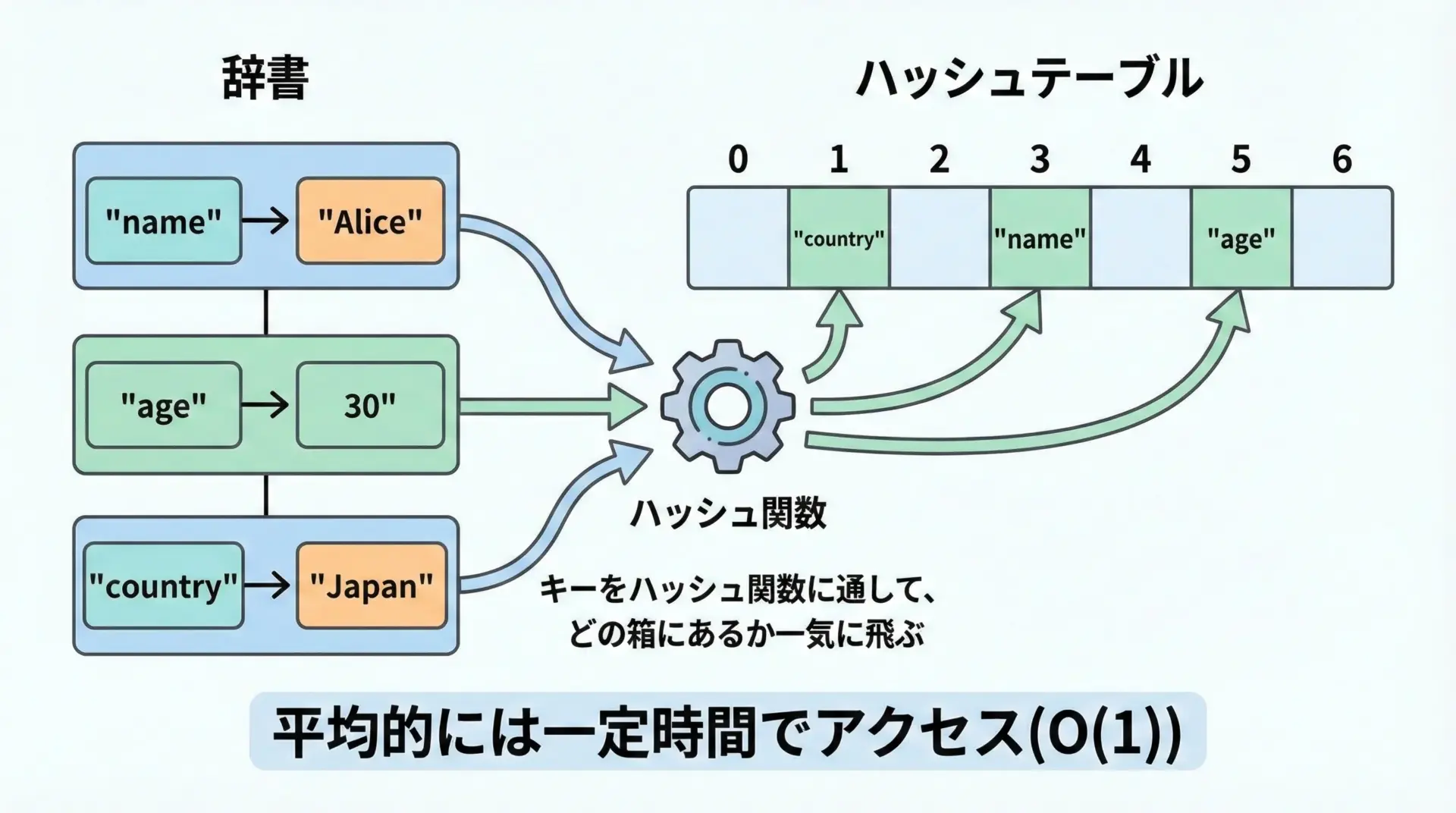
CPythonの実際の挙動はかなり複雑ですが、イメージとしては次のような流れになります。
- キーからハッシュ値を計算する
- ハッシュ値から、内部配列のインデックスを求める
- そのインデックス位置(もしくは衝突時は別の位置)に、目的のキーが存在するかを確認する
このように「飛び先」を直接計算するため、リストのように先頭から順に走査する必要がありません。
セットのinは要素検索で平均O(1)
セット(set)は、重複を持たない要素集合であり、内部的には辞書と同じくハッシュテーブルを使って実装されています。
そのため、in演算子の計算量も辞書と同じく平均O(1)です。
fruits = {"apple", "banana", "orange"}
print("apple" in fruits) # True
print("grape" in fruits) # Falseセットでは、要素そのものが「キー」の役割を果たしています。
したがって、何かの「集合」に属するかどうかを判定する用途では、セットに対するinが最もシンプルで高速です。
ハッシュテーブルによる高速化の仕組み
辞書やセットが高速である理由は、ハッシュテーブルというデータ構造にあります。
ここでは、詳細なアルゴリズムではなく、仕組みを直感的に理解することを目指します。
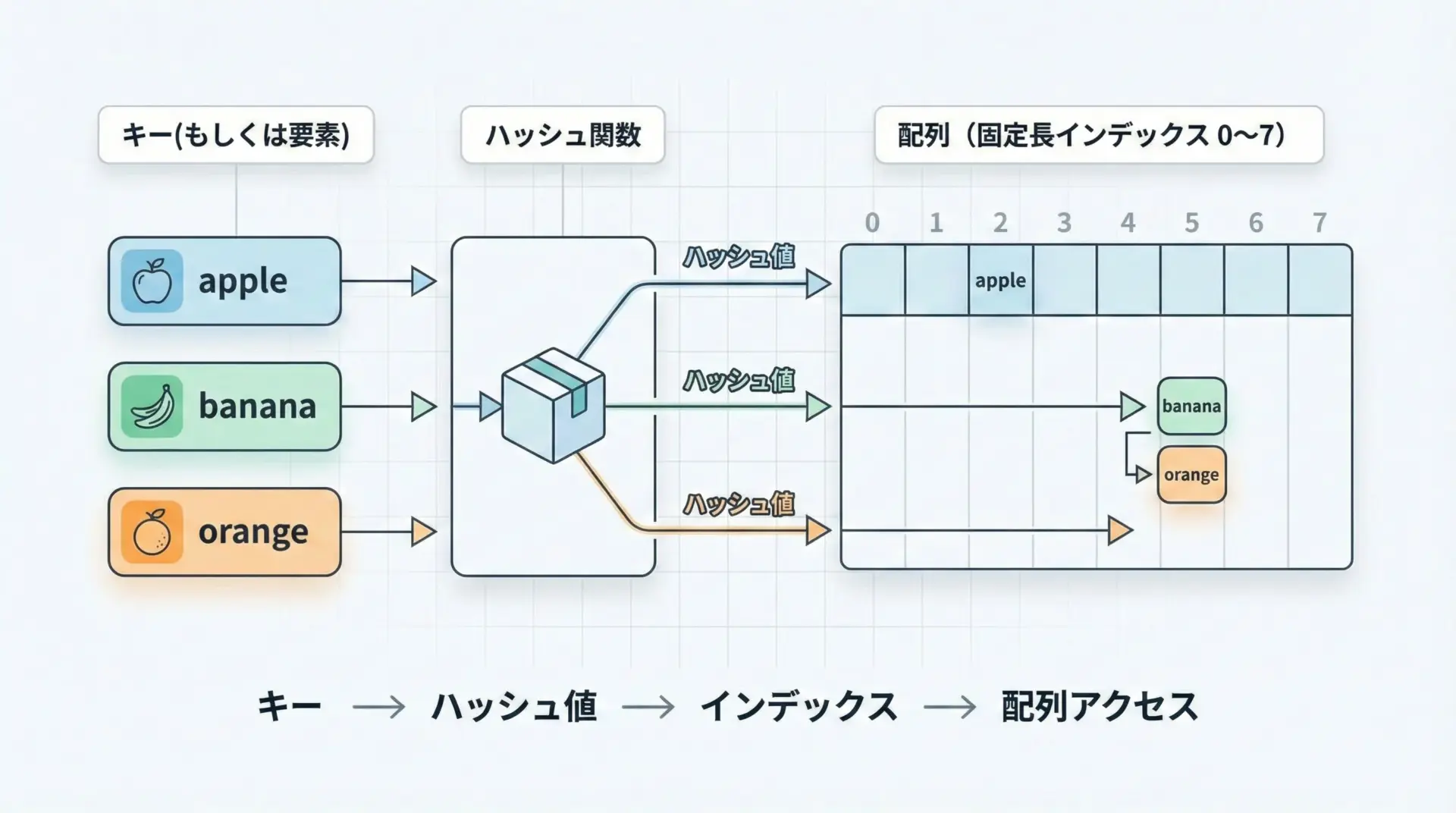
ハッシュテーブルの大まかな流れは次のようになります。
- キー(または要素)から、ハッシュ関数で整数値(ハッシュ値)を計算する
- ハッシュ値を、内部配列のサイズで割った余りなどを使ってインデックスに変換する
- そのインデックス位置に、キーと値(または要素)を保存する
- 検索時も同じ手順でインデックスを特定し、そこに目的のキーがあるかを確認する
この「一足飛びで目的の場所に行ける」仕組みのおかげで、要素数が増えても検索時間がほとんど増えないのが、ハッシュテーブルの強みです。
ただし、注意すべき点もあります。
ハッシュ値が衝突した場合(異なるキーが同じインデックスに割り当てられた場合)には、別の位置に退避したり、チェーン構造をたどったりする必要があるため、最悪ケースではO(n)になることがあります。
ただし、よく設計されたハッシュ関数と十分なテーブルサイズがあれば、平均的にはO(1)に近い性能を保つことができます。
辞書とセットでinを使うときの注意点
辞書やセットのinは高速ですが、間違いやすいポイントがいくつかあります。
1つ目は、辞書に対するinは「キー」だけを見ているという点です。
値を検索したい場合には、明示的にvalues()を使う必要があります。
user = {"name": "Alice", "age": 30}
print("Alice" in user) # False (キーとしては存在しない)
print("Alice" in user.values()) # True (値に対する検索)
# ただし、values()はリスト相当の線形探索になるためO(n)2つ目は、辞書・セットのキー(要素)にはハッシュ可能(hashable)なオブジェクトしか使えない点です。
たとえば、リストはハッシュ不可能なので、辞書のキーにもセットの要素にもできません。
# これはエラーになる例
invalid_set = { [1, 2, 3] } # TypeError: unhashable type: 'list'3つ目は、巨大な辞書・セットを頻繁に更新すると、再ハッシュ(rehash)や内部配列の拡張コストが発生する点です。
特に、追加・削除を膨大な回数繰り返す場合には、理論上のO(1)から外れて遅く感じる場面も出てきます。
in演算子を速くする実践的な選び方
リスト・辞書・セットの使い分け指針
ここまでの内容を踏まえて、Pythonでin演算子を使うときに、どのデータ構造を選ぶべきかの指針をまとめます。
| 用途のイメージ | 適したデータ構造 | 理由 |
|---|---|---|
| 順番が大事な単なる並び(小規模) | リスト(list) | 挿入・削除・スライスが簡単で、要素数が少なければinのコストも小さい |
| 「この集合に含まれるか」を頻繁に判定 | セット(set) | 高速なメンバーシップ判定が可能で、実装も辞書より単純 |
| 「キー→値」の対応関係を管理しつつ、キーの存在を調べる | 辞書(dict) | キー検索が平均O(1)で、値も同時に扱える |
| 順序も保持したいが、頻繁に検索も行いたい | (3.7以降の)辞書(dict)や、必要に応じてリスト+セットの併用 | dictは挿入順を保持するので、順序と高速検索の両方を満たせる |
検索が主目的なら、まずはセットか辞書を使うことを検討し、順序や重複の必要性によってリストとの使い分けを行うのが実用的な方針です。
要素数とin演算子のパフォーマンス比較の目安
次に、要素数と性能の関係をもう少し具体的にイメージしてみます。
以下はあくまで目安ですが、実務における判断の参考になります。
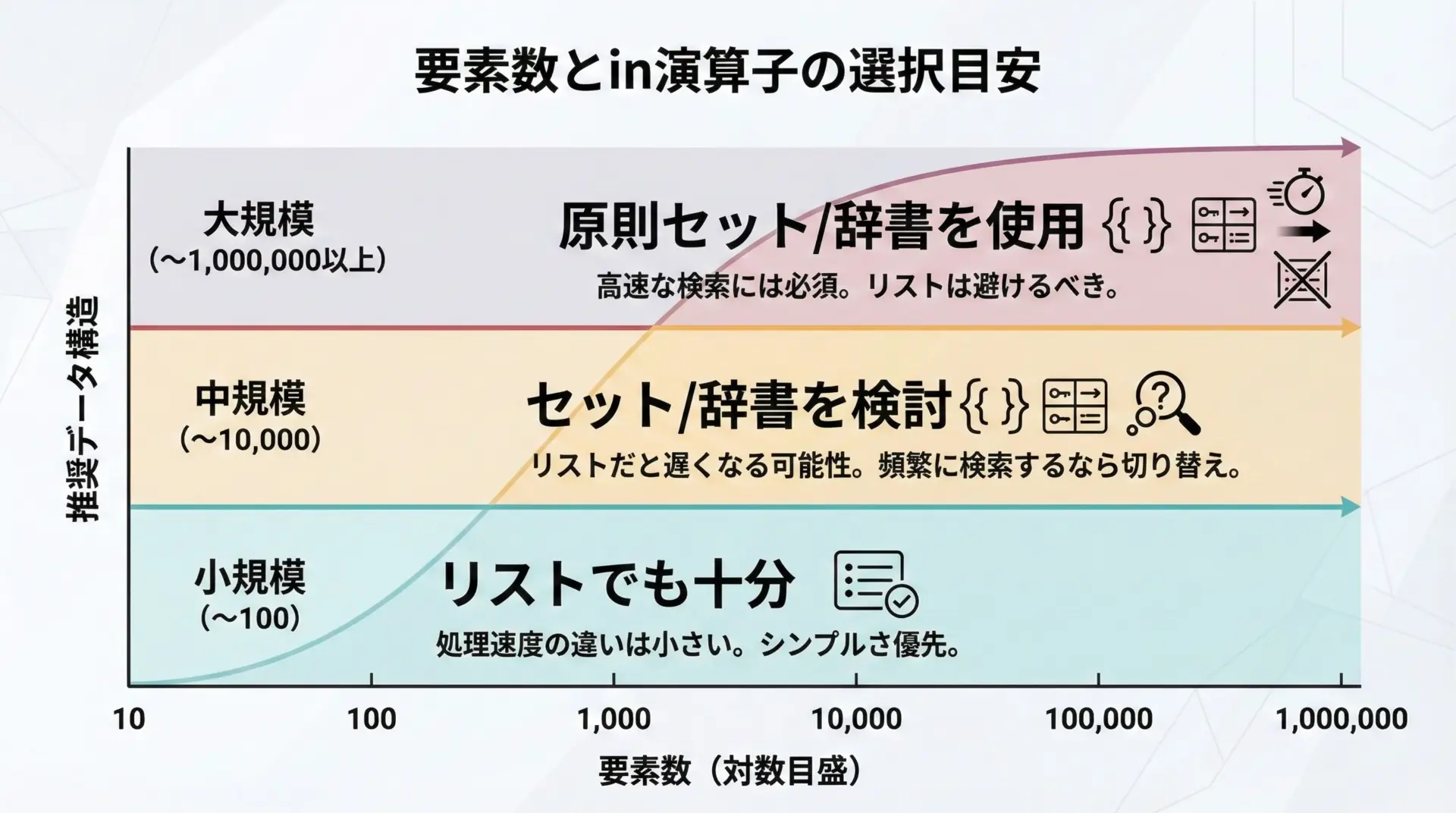
おおまかな目安として、次のように考えると分かりやすいです。
- 要素数が数十〜数百程度であれば、リストの
inでも十分なことが多いです。コードのシンプルさを優先して問題ありません。 - 要素数が数千〜数万程度になり、かつ検索回数が多い場合には、セットや辞書の利用を真剣に検討すべきです。
- 要素数が数十万〜数百万規模では、基本的にセットや辞書を前提とした設計にしないと、検索性能がボトルネックになりやすくなります。
簡単なベンチマークコードで、リスト・セット・辞書の違いを確認してみましょう。
import time
def build_structures(n):
lst = list(range(n))
st = set(range(n))
dct = {i: None for i in range(n)}
return lst, st, dct
def measure_membership(container, target, trials=1000):
start = time.perf_counter()
for _ in range(trials):
_ = target in container
end = time.perf_counter()
return end - start
n = 100_000 # 要素数10万
lst, st, dct = build_structures(n)
target = n + 1 # 存在しない値(最悪ケース)
for name, container in [("list", lst), ("set", st), ("dict", dct)]:
elapsed = measure_membership(container, target)
print(f"{name:>4} の in 判定時間: {elapsed:.6f} 秒")上記のようなコードを実行すると、環境差はあるものの、リストとセット/辞書の間に数十倍〜数百倍程度の差が出ることも珍しくありません。
計算量を意識したPythonコード最適化のポイント
最後に、Pythonコードでin演算子を使う際に、パフォーマンスを意識した書き方のポイントをいくつか整理します。
1. 繰り返し処理の外側でデータ構造を構築する
よくあるアンチパターンとして、ループのたびにリストやセットを再構築してしまう書き方があります。
これは、データ構造の構築コストがループ回数分だけ無駄に繰り返されてしまうため、非常に非効率です。
# 悪い例: 毎回list(...)を作り直している
candidates = [1, 2, 3, 4, 5]
for x in range(100000):
if x in list(candidates): # ループごとに新しいリストが生成される
...# 良い例: ループの外側で集合構造を作っておく
candidates = {1, 2, 3, 4, 5} # setにしておくと in が高速
for x in range(100000):
if x in candidates:
...判定対象となる集合は、可能な限り一度だけ作成し、ループ内では再利用するのが鉄則です。
2. リストからセット・辞書への変換を検討する
既にリストとしてデータを持っている場合でも、検索を大量に行う場面だけ、セットに変換して使うという方法が有効です。
items = ["apple", "banana", "orange", "grape", "melon"]
queries = ["banana", "melon", "mango"] * 10000 # 検索したい単語が大量にある
# setに変換してから検索する
item_set = set(items)
count = 0
for q in queries:
if q in item_set: # 高速なO(1)検索
count += 1
print("ヒット件数:", count)変換自体にはO(n)のコストがかかりますが、その後に行う検索回数が多ければ、多くの場合で元が取れます。
3. 辞書のキー検索と値検索を混同しない
辞書で値の存在を調べたいときに、誤ってinを使うと、期待しない結果になります。
また、values()を使うと今度は線形探索になることにも注意が必要です。
user = {"name": "Alice", "age": 30}
# 名前が辞書の「値」として含まれているかを調べたい場合
# (この操作自体が本当に必要か、設計から見直した方が良いことも多い)
if "Alice" in user.values(): # O(n)の線形探索
...もし、「名前→ユーザ情報」という逆引きを頻繁に行う必要があるなら、最初から「名前をキー」にした別の辞書を用意する方がパフォーマンスには有利です。
まとめ
Pythonのin演算子は一見シンプルですが、対象とするデータ構造によって内部の挙動と計算量が大きく変わります。
リストのinは線形探索でO(n)、辞書とセットのinはハッシュテーブルに基づく平均O(1)の高速検索です。
要素数が増えるほど、この違いは顕著になります。
検索回数が多い処理では、リストをそのまま使うのではなく、セットや辞書への変換を検討することが重要です。
順序や重複の必要性、要素数、更新頻度などを総合的に考慮し、計算量を意識したデータ構造の選択を行うことで、Pythonプログラムのパフォーマンスを大きく改善できます。

