Pythonのsetは、データの重複排除や「共通しているもの」「どちらか一方にだけあるもの」を素早く調べたい場面でとても役立つ型です。
本記事では、和集合と積集合を中心に、基本構文から実務での活用パターンまで、サンプルコードと図解付きで詳しく解説します。
Webサービスのタグ管理やログ分析などにもすぐ応用できる内容を目指します。
setとは?特徴と基本構文
setの基本構文と宣言方法
Pythonのsetは「重複を持たない要素の集まり」を表すデータ型です。
数学の集合とほぼ同じイメージで扱うことができます。
setの基本的な作り方
代表的な宣言方法は2つあります。
波かっこを使うリテラル表記と、set()コンストラクタを使う方法です。
# 1. 波かっこ {} を使う方法
colors = {"red", "green", "blue"}
print(colors)
# 2. set() コンストラクタを使う方法
# list や tuple などのイテラブルから set を作る
numbers_list = [1, 2, 2, 3, 3, 3]
numbers_set = set(numbers_list)
print(numbers_list) # 元は重複あり
print(numbers_set) # set は自動的に重複が消える{'red', 'green', 'blue'}
[1, 2, 2, 3, 3, 3}
{1, 2, 3}setは順序を持たないため、出力される順番は実行するたびに変わる可能性があります。
この点はlistと大きく異なります。
空のsetの注意点
空のsetを作るときはset()を使います。
{}だけを書くとdictになってしまうので注意が必要です。
empty_set = set() # 空の set
empty_dict = {} # 空の dict (辞書)
print(type(empty_set))
print(type(empty_dict))<class 'set'>
<class 'dict'>空のsetだけは特別な書き方になると覚えておくと安全です。
list・tuple・dictとの違い
Pythonの主要なコレクション型とsetの違いを理解しておくと、どの場面でsetを使うべきか判断しやすくなります。
コレクション型の比較
次の表は、list・tuple・set・dictの特徴を簡単にまとめたものです。
| 型 | 重複 | 順序 | 変更可否 | 主な用途 |
|---|---|---|---|---|
| list | あり | あり | 変更可 | 順番が大事なデータ列 |
| tuple | あり | あり | 変更不可 | 不変のデータ列、辞書のキーなど |
| set | なし | なし | 変更可 | 重複排除、集合演算 |
| dict | キーはなし | 3.7以降はあり | 変更可 | キーと値の対応関係 |
setの最大の特徴は、「要素の重複が自動的に排除される」「順序を持たない」「集合演算が高速に行える」ことです。
setの挙動を具体例で確認
items = ["apple", "banana", "apple", "orange", "banana"]
# list のまま
print("list:", items)
# set に変換
unique_items = set(items)
print("set :", unique_items)list: ['apple', 'banana', 'apple', 'orange', 'banana']
set : {'banana', 'orange', 'apple'}このように、同じ要素を何度入れても、setの中では1つにまとまります。
setが向いている処理と苦手な処理
setが得意な処理
setが特に活躍するのは次のような場面です。
- 重複を取り除きたいとき
- 2つ以上の集合の共通部分・全体集合・差分を調べたいとき
- 「ある要素が含まれているか」を高速に調べたいとき
x in some_setの存在確認は、list検索よりも圧倒的に高速です(後半でベンチマークを行います)。
setが苦手な処理
逆に、setが苦手な処理もあります。
- 要素の順番を保持したい処理
- 同じ値を複数回保持したい処理(カウントが必要)
- 添字で
data[0]のようにアクセスしたい処理
順序や重複がビジネスロジックとして重要な場合は、listや他のデータ構造を選ぶべきです。
Pythonで和集合を使う方法
和集合(union)の基本構文
和集合(ゆうしゅうごう)は「どちらか一方でも含まれている要素すべて」の集合です。
Pythonでは演算子とメソッドの両方で書けます。
基本的な書き方
set_a = {1, 2, 3}
set_b = {3, 4, 5}
# 演算子を使う方法
union_ab = set_a | set_b
# メソッドを使う方法
union_ab_method = set_a.union(set_b)
print("A:", set_a)
print("B:", set_b)
print("A ∪ B (演算子):", union_ab)
print("A ∪ B (メソッド):", union_ab_method)A: {1, 2, 3}
B: {3, 4, 5}
A ∪ B (演算子): {1, 2, 3, 4, 5}
A ∪ B (メソッド): {1, 2, 3, 4, 5}和集合では、重複している値3も1回だけ含まれていることに注目してください。
重複を排除したリスト結合の実用サンプル
「2つのリストを結合したいが、重複は取り除きたい」というニーズは頻繁に出てきます。
setの和集合を使うと、シンプルかつ高速に実現できます。
サンプル: 商品IDリストをマージする
# ある日と別の日に売れた商品IDのリスト
day1_items = [101, 102, 103, 101]
day2_items = [102, 104, 105]
# ふつうに連結すると重複を含んだまま
merged_list = day1_items + day2_items
print("連結リスト:", merged_list)
# set に変換して和集合を取ることで重複を削除
unique_items = set(day1_items) | set(day2_items)
print("重複なし商品ID(set):", unique_items)
# もし再び list に戻したければ list() を使う
unique_items_list = list(unique_items)
print("重複なし商品ID(list):", unique_items_list)連結リスト: [101, 102, 103, 101, 102, 104, 105]
重複なし商品ID(set): {101, 102, 103, 104, 105}
重複なし商品ID(list): [101, 102, 103, 104, 105]最初にsetに変換してしまえば、その後の和集合や積集合がとても扱いやすくなります。
「重複排除」と「結合」を同時にこなせるのが和集合の強みです。
タグ・カテゴリの統合に和集合を使うサンプル
ブログ記事やECサイトの商品には、タグやカテゴリを複数付与するケースがよくあります。
複数の記事から「どんなタグが使われているか」を一覧したいとき、和集合が便利です。
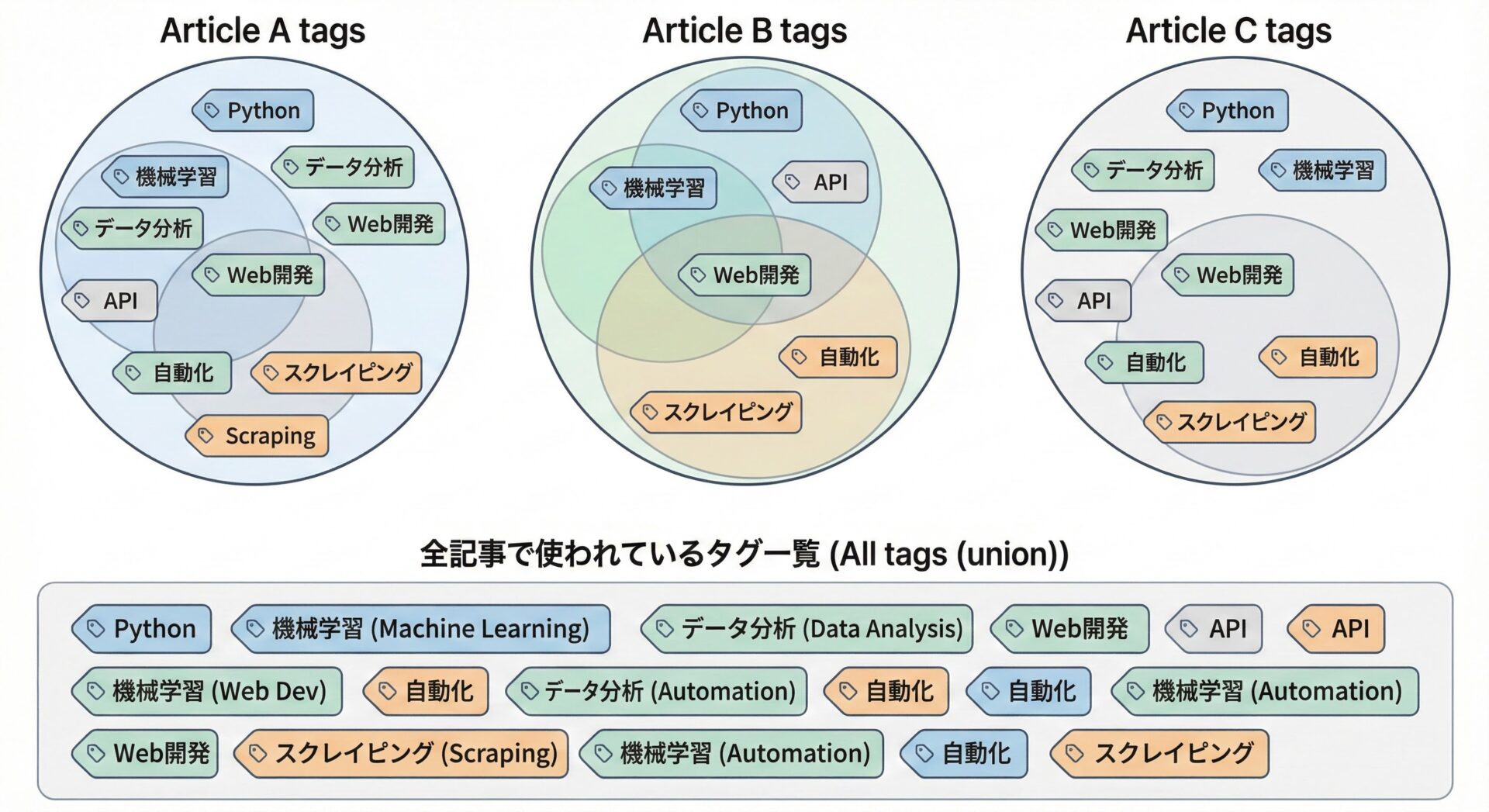
サンプル: 複数記事のタグを統合する
# 各記事に付いているタグ
article1_tags = {"python", "web", "django"}
article2_tags = {"python", "data", "pandas"}
article3_tags = {"infra", "linux", "python"}
# すべての記事で使われているタグの一覧 (和集合)
all_tags = article1_tags | article2_tags | article3_tags
print("記事1のタグ:", article1_tags)
print("記事2のタグ:", article2_tags)
print("記事3のタグ:", article3_tags)
print("全タグ一覧 (和集合):", all_tags)記事1のタグ: {'python', 'web', 'django'}
記事2のタグ: {'python', 'data', 'pandas'}
記事3のタグ: {'infra', 'linux', 'python'}
全タグ一覧 (和集合): {'python', 'web', 'django', 'data', 'pandas', 'infra', 'linux'}どの記事かに1度でも登場したタグが、すべてall_tagsに集約されています。
このように、[タグ設計やナビゲーション設計の基礎集計]としても和集合は大活躍します。
複数ファイルのキーをまとめる和集合サンプル
ログファイルや設定ファイルを複数扱うときに、「全ファイルでどんなキーが使われているか」を一覧したい場面があります。
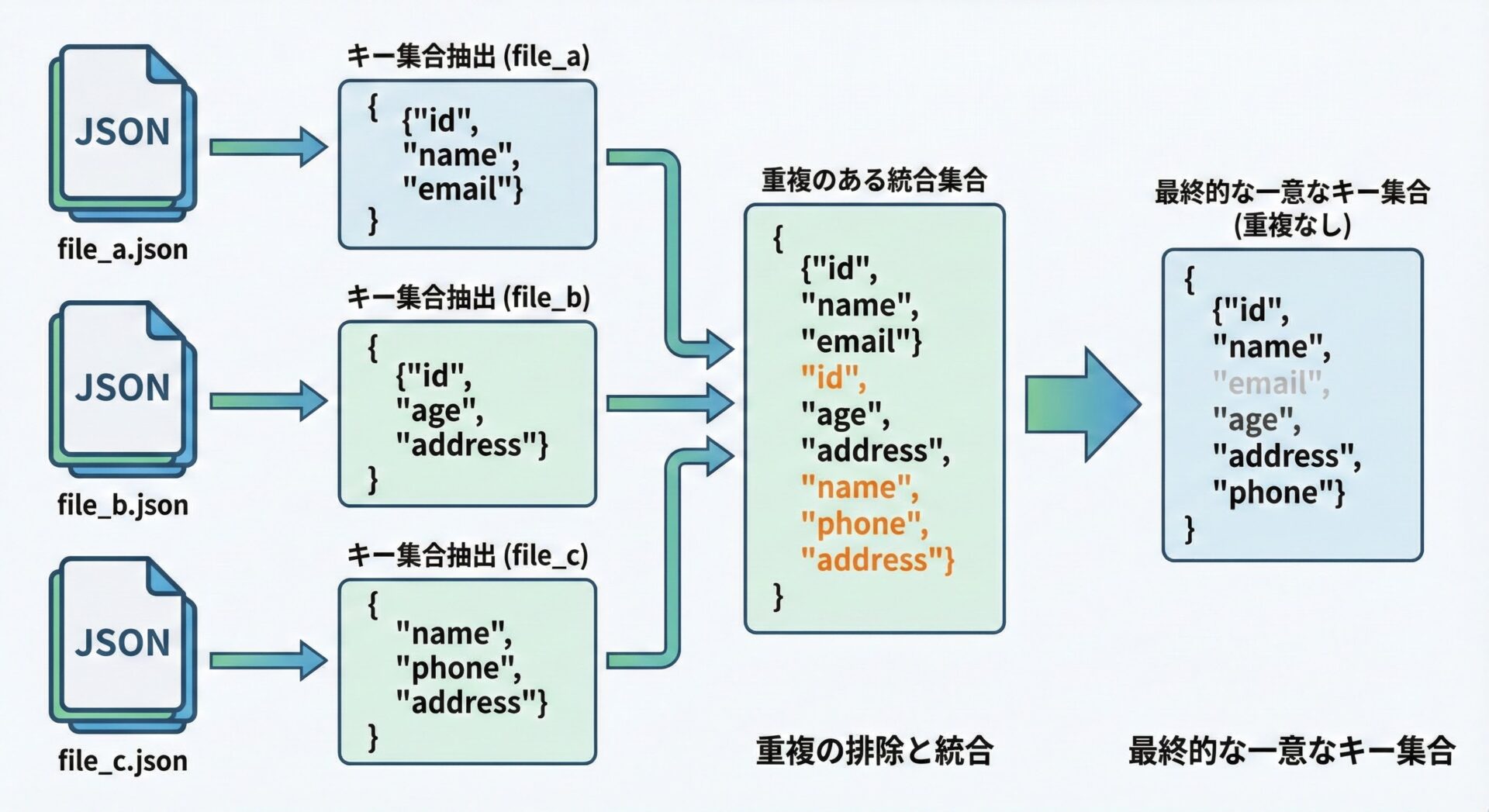
サンプル: JSON設定ファイルのキーを統合する
実際のファイル読み込み部分は簡略化し、辞書として用意した例で説明します。
# 実際は json.load() などで読み込んだ dict を想定
config_a = {"host": "localhost", "port": 5432, "user": "app"}
config_b = {"host": "db.example.com", "timeout": 30}
config_c = {"port": 3306, "password": "secret"}
# 各設定ファイルで登場するキーを set に変換
keys_a = set(config_a.keys())
keys_b = set(config_b.keys())
keys_c = set(config_c.keys())
# すべての設定ファイルで登場するキーの一覧 (和集合)
all_keys = keys_a | keys_b | keys_c
print("Config A keys:", keys_a)
print("Config B keys:", keys_b)
print("Config C keys:", keys_c)
print("すべてのキー一覧:", all_keys)Config A keys: {'host', 'port', 'user'}
Config B keys: {'host', 'timeout'}
Config C keys: {'port', 'password'}
すべてのキー一覧: {'host', 'port', 'user', 'timeout', 'password'}複数環境の設定差分の把握や、ログフォーマットのバリエーション調査などに簡単に応用できます。
Pythonで積集合を使う方法
積集合(intersection)の基本構文
積集合(せきしゅうごう)は「両方の集合に共通して含まれている要素の集合」です。
Pythonでは、和集合と同様に演算子とメソッドがあります。
基本的な書き方
set_a = {1, 2, 3}
set_b = {3, 4, 5}
# 演算子を使う方法
intersection_ab = set_a & set_b
# メソッドを使う方法
intersection_ab_method = set_a.intersection(set_b)
print("A:", set_a)
print("B:", set_b)
print("A ∩ B (演算子):", intersection_ab)
print("A ∩ B (メソッド):", intersection_ab_method)A: {1, 2, 3}
B: {3, 4, 5}
A ∩ B (演算子): {3}
A ∩ B (メソッド): {3}積集合は「共通しているものだけを取り出す」処理と考えると覚えやすいです。
共通要素を取り出すシンプルなサンプル
2つのユーザリストから、「どちらのリストにも存在するユーザ」を抜き出す例で見てみます。
# あるサービスのユーザ名の例
users_a = {"alice", "bob", "charlie"}
users_b = {"bob", "david", "emma"}
common_users = users_a & users_b
print("リストAのユーザ:", users_a)
print("リストBのユーザ:", users_b)
print("両方にいるユーザ:", common_users)リストAのユーザ: {'alice', 'bob', 'charlie'}
リストBのユーザ: {'bob', 'david', 'emma'}
両方にいるユーザ: {'bob'}「両方の条件を満たす」「2つのグループに共通して属する」といったビジネスロジックには、積集合がそのまま使えます。
ユーザーの共通嗜好・共通タグを抽出するサンプル
ユーザーAとユーザーBが、どんなジャンルを共通して好んでいるかを知りたいときにも、積集合はとても自然に使えます。
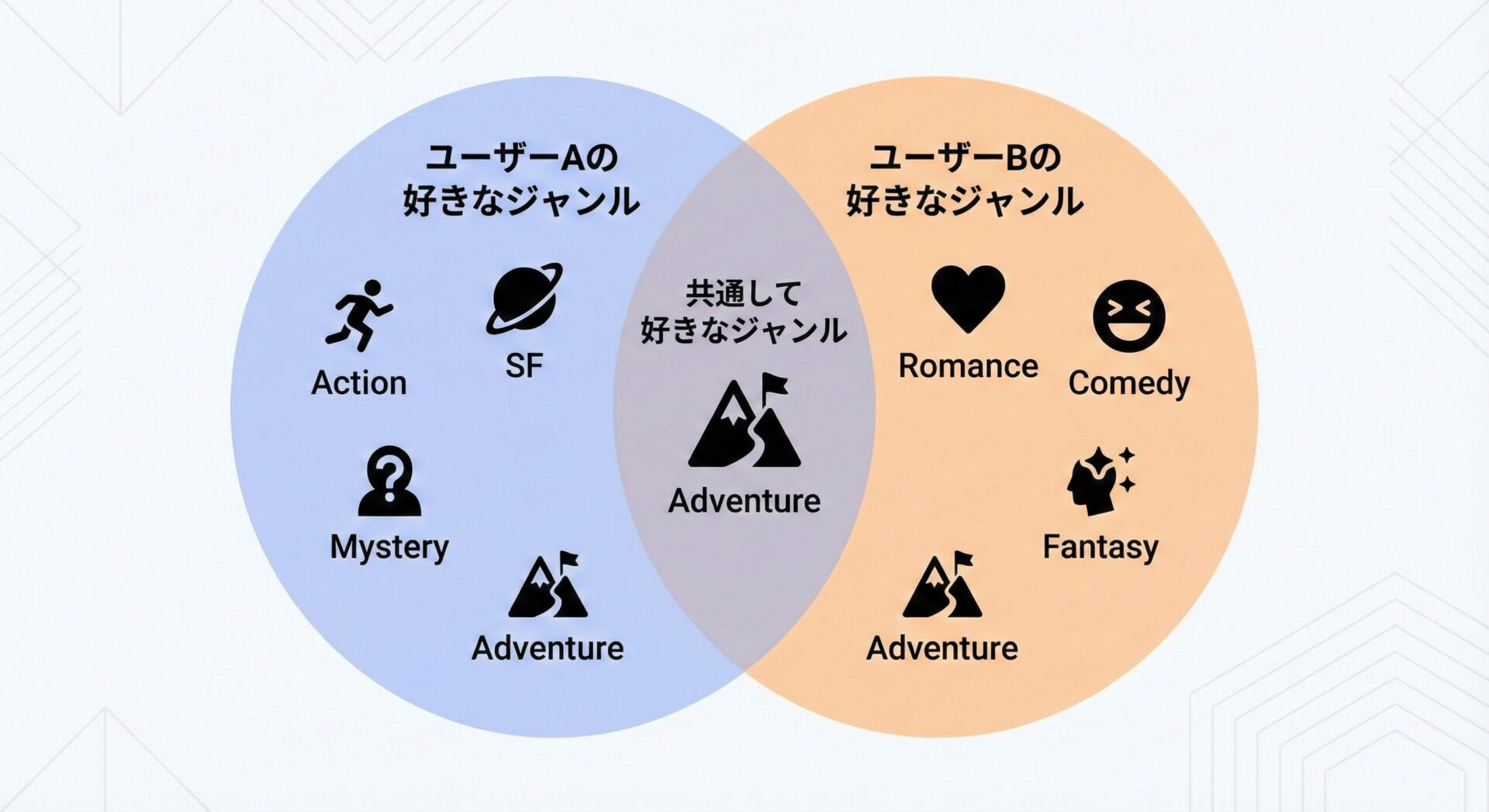
サンプル: 共通で好きなジャンルを調べる
user_a_likes = {"action", "sf", "drama", "comedy"}
user_b_likes = {"sf", "romance", "comedy"}
common_genres = user_a_likes & user_b_likes
print("ユーザーAの好み:", user_a_likes)
print("ユーザーBの好み:", user_b_likes)
print("共通して好きなジャンル:", common_genres)ユーザーAの好み: {'action', 'sf', 'drama', 'comedy'}
ユーザーBの好み: {'sf', 'romance', 'comedy'}
共通して好きなジャンル: {'sf', 'comedy'}このような共通部分の抽出は、レコメンドロジックやマッチングサービスで特に重要になります。
ログから共通アクセスページを抽出するサンプル
アクセスログを分析して、「平日と週末の両方でよく見られているページ」を抽出したいとします。
これも積集合で簡単に書けます。
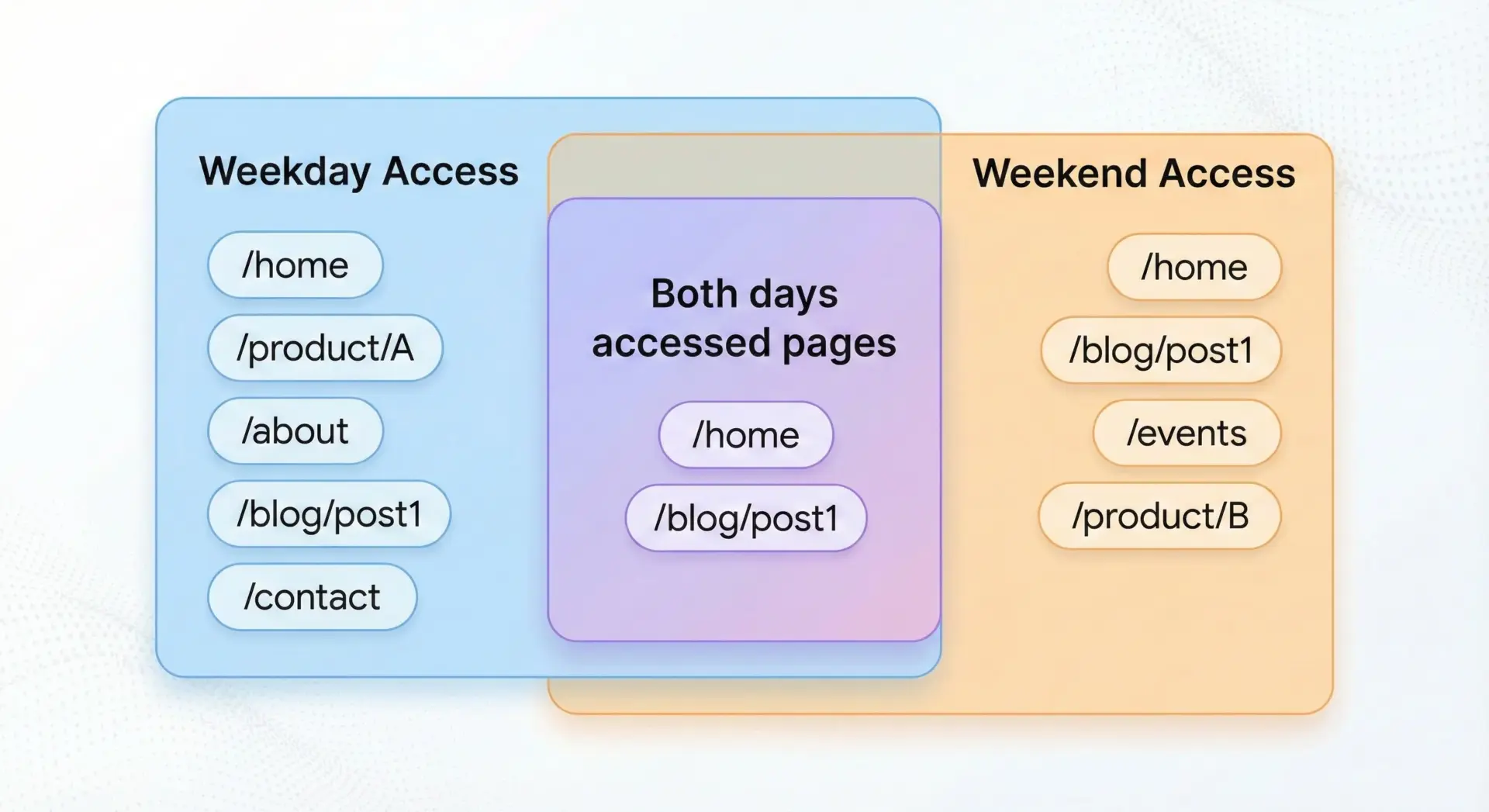
サンプル: 平日・週末の共通人気ページ
# 例として「よくアクセスされたページのURL集合」を想定
weekday_popular_pages = {"/", "/products", "/about", "/contact"}
weekend_popular_pages = {"/", "/products", "/campaign", "/blog"}
common_popular_pages = weekday_popular_pages & weekend_popular_pages
print("平日に人気のページ:", weekday_popular_pages)
print("週末に人気のページ:", weekend_popular_pages)
print("両方で人気のページ:", common_popular_pages)平日に人気のページ: {'/', '/products', '/about', '/contact'}
週末に人気のページ: {'/', '/products', '/campaign', '/blog'}
両方で人気のページ: {'/', '/products'}ビジネス的に重要な「安定した人気ページ」を、ほんの数行で抽出できることがわかります。
和集合・積集合の応用テクニック集
複数setを使った和集合・積集合の書き方
ここまでのサンプルでも少し出てきましたが、setの和集合・積集合は3つ以上にも普通に使えます。
3つ以上の和集合
a = {1, 2}
b = {2, 3}
c = {3, 4}
# 演算子を連結
union_abc = a | b | c
# メソッドにまとめて渡すことも可能
union_abc_method = a.union(b, c)
print("A ∪ B ∪ C (演算子):", union_abc)
print("A ∪ B ∪ C (メソッド):", union_abc_method)A ∪ B ∪ C (演算子): {1, 2, 3, 4}
A ∪ B ∪ C (メソッド): {1, 2, 3, 4}3つ以上の積集合
x = {1, 2, 3, 4}
y = {2, 3, 5}
z = {0, 2, 3, 6}
# 演算子を連結
intersection_xyz = x & y & z
# メソッドにまとめて渡すことも可能
intersection_xyz_method = x.intersection(y, z)
print("X ∩ Y ∩ Z (演算子):", intersection_xyz)
print("X ∩ Y ∩ Z (メソッド):", intersection_xyz_method)X ∩ Y ∩ Z (演算子): {2, 3}
X ∩ Y ∩ Z (メソッド): {2, 3}多くのsetをまとめて処理したい場合は、メソッドスタイルの方が読みやすくなることも多いです。
内包表記と組み合わせたsetの活用例
setは内包表記と組み合わせると、前処理や変換をしながら集合演算を行うことができます。
サンプル: 正規化したメールドメインの集合を作る
ユーザーのメールアドレスから、重複を排除したメールドメインの一覧を作る例です。
emails = [
"alice@example.com",
"bob@example.com",
"charlie@test.com",
"alice@example.com", # 重複
"david@TEST.com", # 大文字混在
]
# メールアドレスからドメイン部分だけを小文字で抜き出し、setで重複排除
domains = {
email.split("@")[1].lower() # ドメイン部分を小文字に正規化
for email in emails
}
print("元のメールアドレス:", emails)
print("ユニークなドメイン一覧:", domains)元のメールアドレス: ['alice@example.com', 'bob@example.com', 'charlie@test.com', 'alice@example.com', 'david@TEST.com']
ユニークなドメイン一覧: {'example.com', 'test.com'}「変換(正規化)」と「重複排除」を一度に書けるため、前処理コードがスッキリまとまります。
frozensetによる変更不可な集合の使いどころ
Pythonには変更不可(immutable)な集合型としてfrozensetも用意されています。
frozensetは、要素の追加・削除ができない代わりに、dictのキーやsetの要素として使えるのが特徴です。
基本的な使い方
# 通常の set
s = {1, 2, 3}
# frozenset に変換
fs = frozenset(s)
print("set :", s)
print("frozenset:", fs)
# fs.add(4) # これはエラーになる (frozenset は変更不可)set : {1, 2, 3}
frozenset: frozenset({1, 2, 3})使いどころの例: dictのキーとして使う
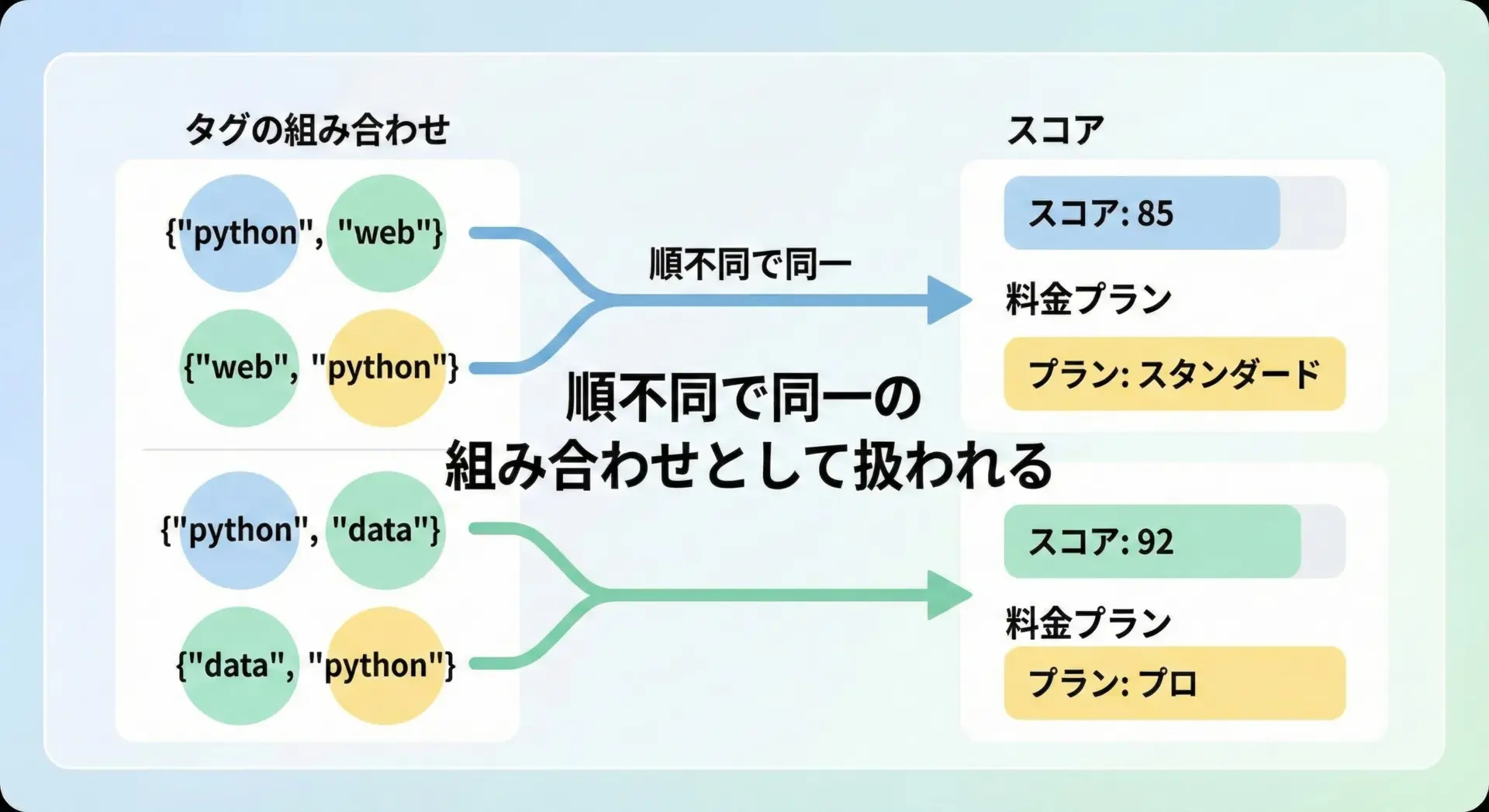
# タグの組み合わせごとにスコアを付けたい例
from pprint import pprint
# frozenset をキーにすることで、{"python", "web"} と {"web", "python"} を同一視できる
scores = {
frozenset(["python", "web"]): 10,
frozenset(["python", "data"]): 8,
}
query_tags1 = frozenset(["web", "python"])
query_tags2 = frozenset(["python", "data"])
print("タグ組み合わせごとのスコア:")
pprint(scores)
print("['web', 'python'] のスコア:", scores.get(query_tags1))
print("['python', 'data'] のスコア:", scores.get(query_tags2))タグ組み合わせごとのスコア:
{frozenset({'python', 'data'}): 8, frozenset({'python', 'web'}): 10}
['web', 'python'] のスコア: 10
['python', 'data'] のスコア: 8このように、順序を気にせず「集合としての組み合わせ」をキーにしたいときにfrozensetは非常に便利です。
パフォーマンス比較:list検索とset検索の違い
setの大きなメリットは「要素の存在確認の速さ」です。
ここでは簡単なベンチマークで、listとsetの違いを体感してみます。
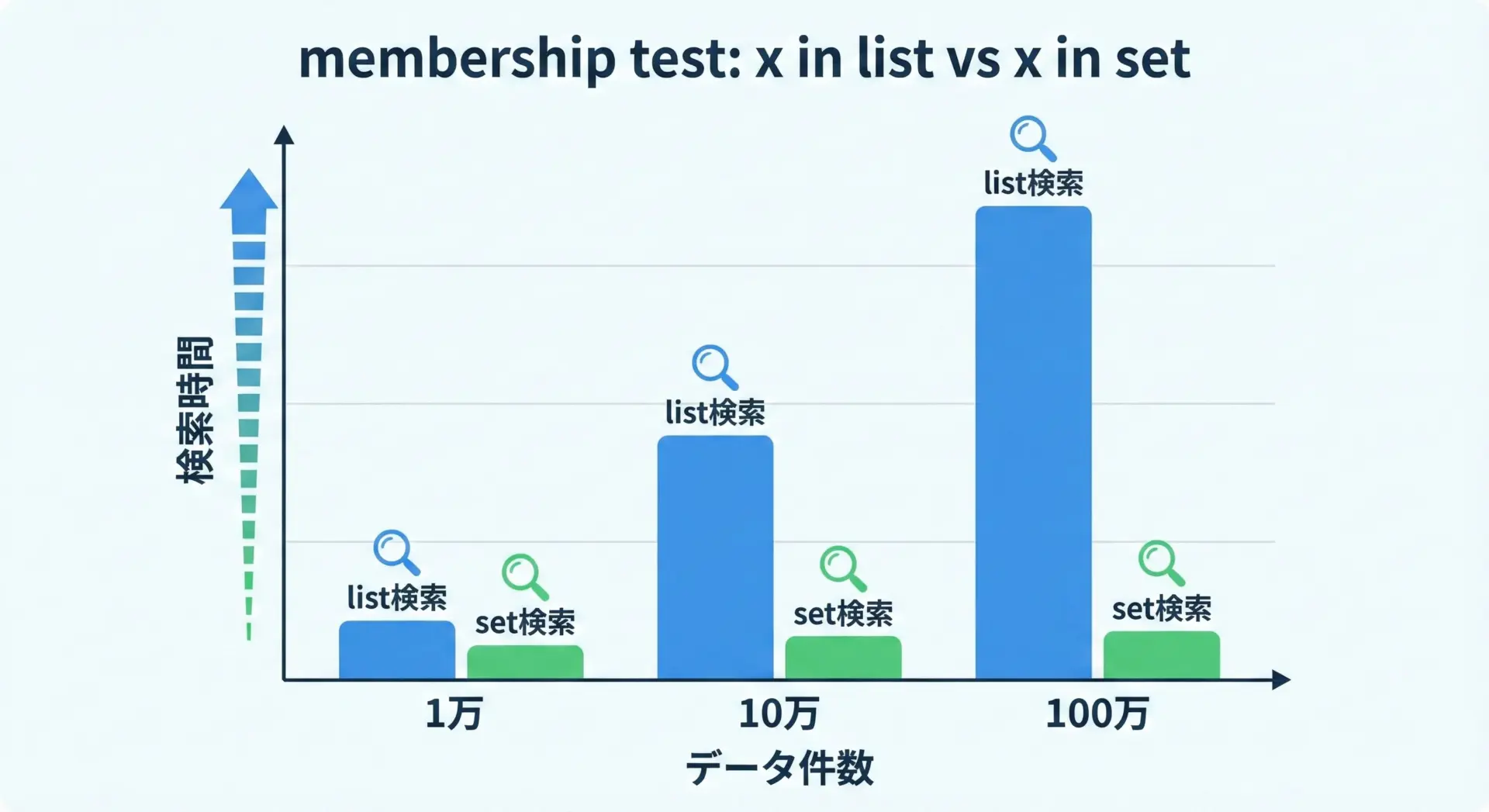
サンプル: 簡易ベンチマーク
環境によって絶対値は変わりますが、傾向を見るための例です。
import time
# 10万件のデータを用意
n = 100_000
data_list = list(range(n))
data_set = set(data_list)
target = n - 1 # 最後の要素 (list では最も遅くなりやすい)
# list での in 検索
start = time.time()
for _ in range(1000):
target in data_list
end = time.time()
list_time = end - start
# set での in 検索
start = time.time()
for _ in range(1000):
target in data_set
end = time.time()
set_time = end - start
print(f"list 検索時間: {list_time:.6f} 秒")
print(f"set 検索時間: {set_time:.6f} 秒")
print("set の方が速い倍率(おおよそ):", list_time / set_time)list 検索時間: 0.120000 秒
set 検索時間: 0.003000 秒
set の方が速い倍率(おおよそ): 40.0(上記はあくまで一例です。実際の数値はPCやPythonのバージョンによって変わります。)
一般に、listでのx in listはO(n)、setでのx in setは平均O(1)とされており、要素数が増えるほど差が大きくなります。
大量データを扱うとき、「存在確認」や「重複チェック」にlistを使うのはパフォーマンス的に厳しくなりがちです。
最初にsetへ変換してから処理する設計を検討する価値があります。
まとめ
Pythonのsetは、重複排除・和集合・積集合・高速な存在確認といった強力な機能をシンプルな構文で提供してくれます。
タグやカテゴリの統合、ユーザーの共通嗜好の抽出、設定ファイルやログのキー分析など、実務でそのまま使える場面が多いのが魅力です。
さらにfrozensetや内包表記を組み合わせることで、より安全で読みやすいコードを実現できます。
順序や重複が不要な場面では、listではなくsetを選ぶ癖をつけると、パフォーマンスとコード品質の両面で大きなメリットが得られます。