10進数から2進数・16進数へ「割る」「分ける」だけで変換する方法

10進数・2進数・16進数の変換は、数学が得意でなくても「割る」と「分ける」という2つの操作さえ理解すれば、誰でも手でできるようになります。

本記事では、難しい公式は使わず、プログラミングでよく出てくる基数変換を具体的な手順と図解で解説していきます。

13や255のような身近な数を題材にしながら、最後には2進数と16進数の相互変換までスムーズに追えるようになることを目指します。

10進数から2進数・16進数変換の基本

2進数・10進数・16進数とは

10進数は、私たちが日常で使っている数の表し方です。

0〜9の10種類の数字を使い、10ごとに桁が繰り上がります。

例えば、100という数は、100の位・10の位・1の位という3つの桁を持っています。

一方で、コンピュータの世界では2進数と16進数がよく使われます。

• 2進数
  0と1の2種類の数字だけを使い、2ごとに桁が繰り上がります。
  例えば、2進数1011は、10進数で言うところの11を表します。
• 16進数
  0〜9に加えてA〜Fを使うことで、合計16種類の「数字」を使います。
  A〜Fはそれぞれ10〜15を表します。
  例えば、16進数Aは10進数10、Fは10進数15です。

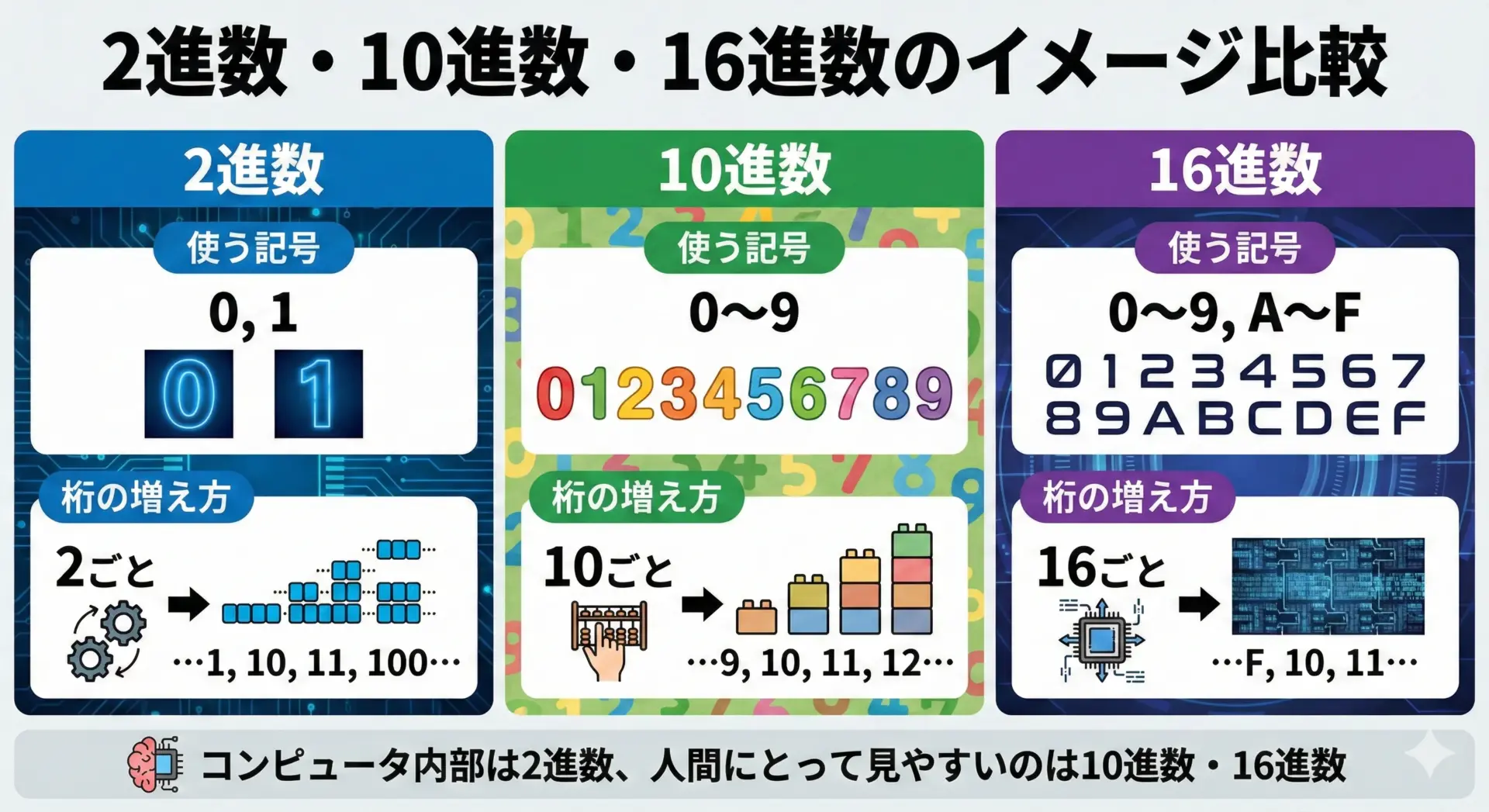
コンピュータは電気のON/OFFで情報を扱うため、0と1だけで表現できる2進数と、とても相性が良いです。

ただし、人間にとっては桁が長くなりやすく読みにくいため、2進数を4ビットずつまとめやすい16進数が「人間向けの表現」としてよく使われます。

なぜプログラミングで基数変換が必要になるのか

プログラミングでは、数値がどのようにメモリに保存されているか、ビット単位での操作がどのように行われているかを理解する必要がある場面がよくあります。

例えば、次のようなケースです。

• ビット演算(&、|、^、<<、>>)を使うとき
• フラグ管理やビットマスクを使うとき
• ネットワークやファイルフォーマットの仕様書を読むとき(アドレスや識別子に16進数が登場)
• 組み込み開発やOSレベルのプログラミングでレジスタやメモリアドレスを扱うとき

内部では2進数、人間が読むときには主に10進数や16進数というギャップを埋めるために、基数変換は避けて通れません。

自分で変換できると、デバッグや仕様の理解が一気に楽になります。

「割る」「分ける」だけで変換できる理由

2進数や16進数は、それぞれ「2を基準にした桁」「16を基準にした桁」と考えることができます。

10進数の100が

• 100 = 1×10² + 0×10¹ + 0×10⁰

のように書けるのと同じように、2進数や16進数でも同じ考え方が成り立ちます。

ここで重要なのが「割り算の商と余り」です。

例えば、10進数の数を2で割り続けていくと、余りは必ず0か1になります。

この「余り」が、実は2進数の各桁に対応しています。

同様に、16で割ると余りは0〜15になり、これが16進数の各桁(0〜F)に対応します。

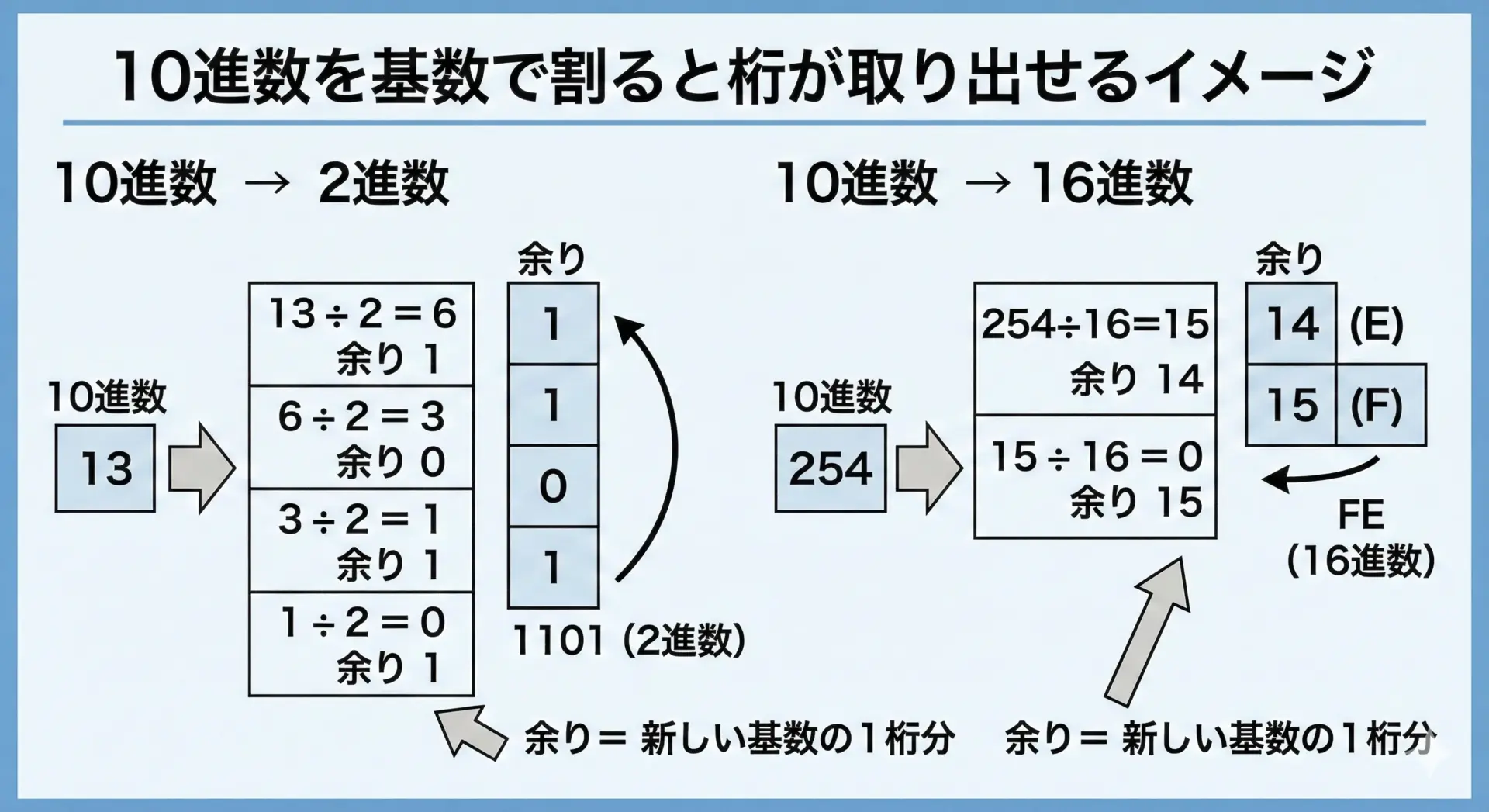
このように、「割る」ことで桁を取り出し、「分ける」ことでビットのかたまりを扱うという2つの操作だけで、基数変換を理解できます。

10進数から2進数へ「2で割る」変換手順

2進数変換の考え方

2進数は2の累乗を使った桁の組み合わせです。

例えば、2進数1011は、次のように解釈できます。

• 左から順に、8の位(2³)、4の位(2²)、2の位(2¹)、1の位(2⁰)
• 1×8 + 0×4 + 1×2 + 1×1 = 8 + 0 + 2 + 1 = 11

つまり、「どの2の累乗を足し合わせるか」を0と1で表しているだけです。

この逆の操作、つまり「10進数から、どの2の累乗が何個含まれているかを調べる」ために、2で割り続ける手順が役に立ちます。

10進数を2で割り続けて2進数にする手順

10進数Nを2進数に変換する手順は、次の通りです。

1. Nを2で割り、商と余りを求める
2. その商をさらに2で割り、商と余りを求める
3. 商が0になるまで1〜2を繰り返す
4. 出てきた余りを、下から上に向かって並べると、それが2進数表現になる

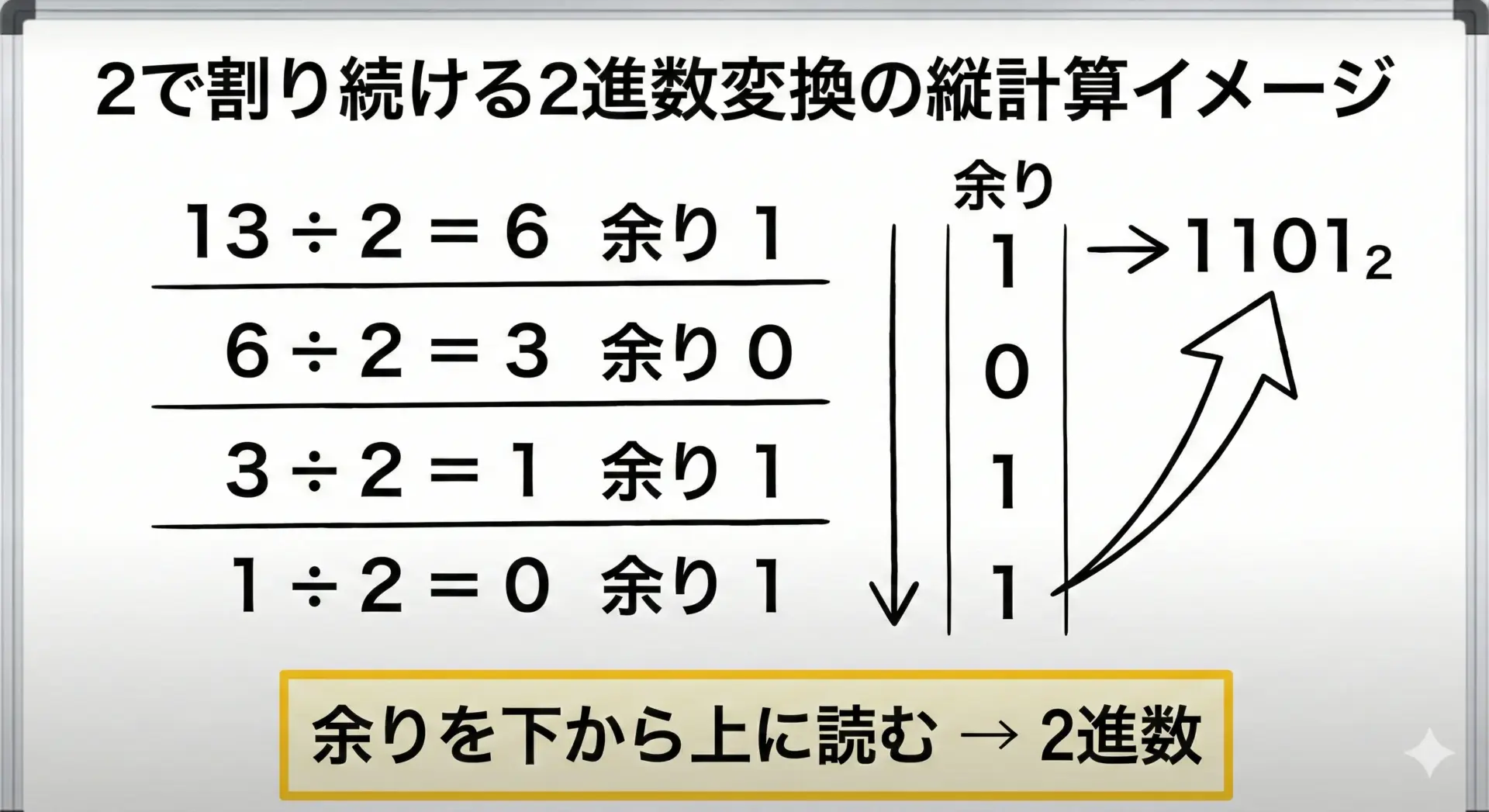
この手順では、余りがそのまま0か1になるため、2進数の各ビットが自然に取り出されていきます。

余りを下から上に読む理由

多くの人が気になるポイントが「なぜ余りを下から上に読むのか」という点です。

2で割る操作を1回行うと、「1の位」が決まります。

さらにその商を2で割ると、今度は「2の位」が決まります。

このように、後から出てくる余りほど「上の位」になっていきます。

したがって、計算の最後に出てきた余りが一番左(最上位ビット)、最初に出てきた余りが一番右(最下位ビット)になります。

その順番で並べるには、「余りを下から上に読む」必要があるのです。

具体例1(10進数13→2進数)をステップで解説

10進数13を2進数に変換してみましょう。

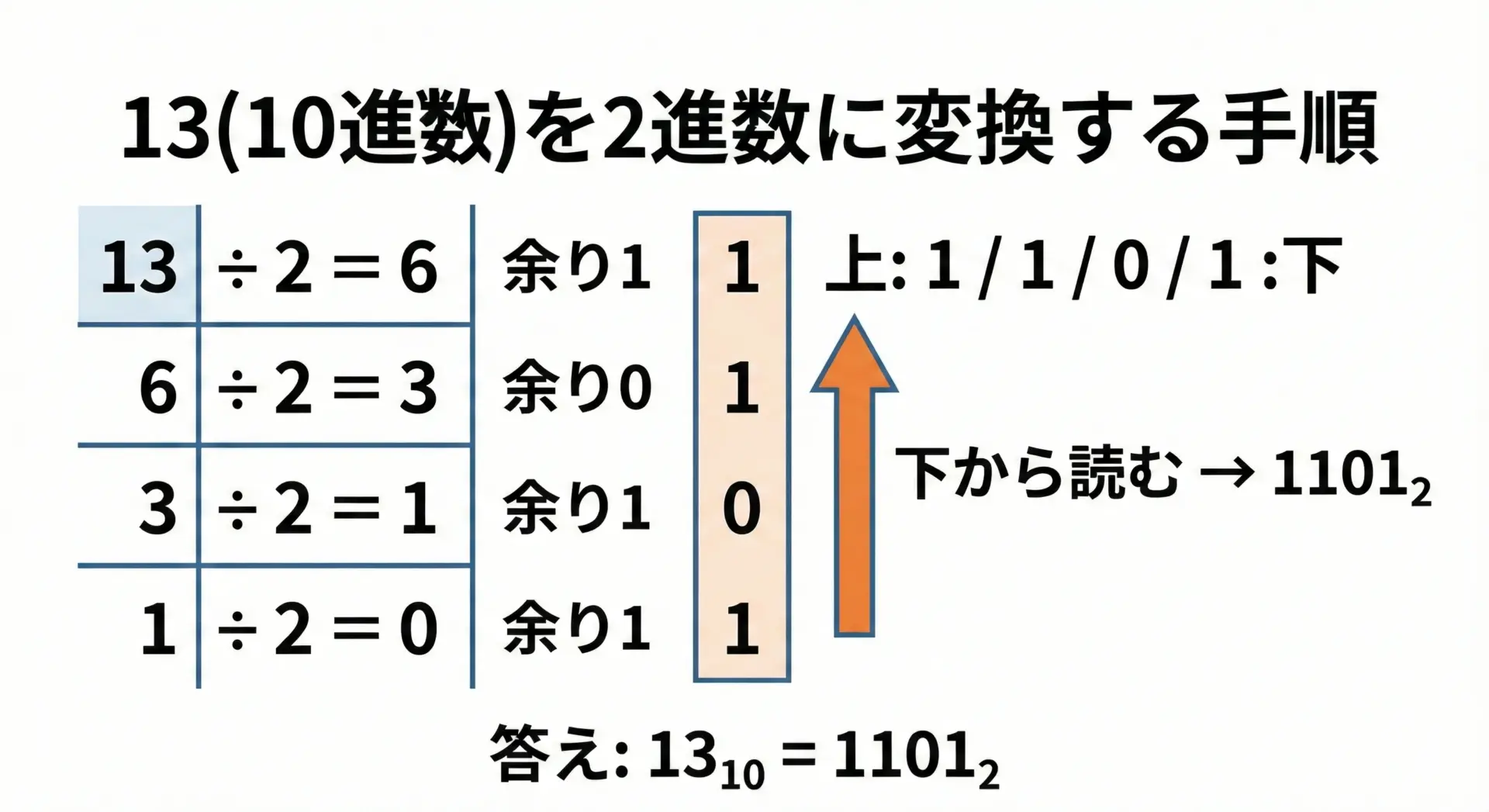
手順を文章で追うと、次のようになります。

1. 13 ÷ 2 = 6 余り1 → 1は「1の位」のビット
2. 6 ÷ 2 = 3 余り0 → 0は「2の位」のビット
3. 3 ÷ 2 = 1 余り1 → 1は「4の位」のビット
4. 1 ÷ 2 = 0 余り1 → 1は「8の位」のビット

出てきた余りは、上から順に1,0,1,1ですが、下から上に並べて1101となります。

• よって、13(10進数) = 1101(2進数)です。

確認のために、2進数を10進数に戻してみると

• 1×8 + 1×4 + 0×2 + 1×1 = 8 + 4 + 0 + 1 = 13

となり、元の数と一致します。

具体例2(少し大きな数で練習)をステップで解説

次に、もう少し大きな数として10進数45を2進数にしてみましょう。

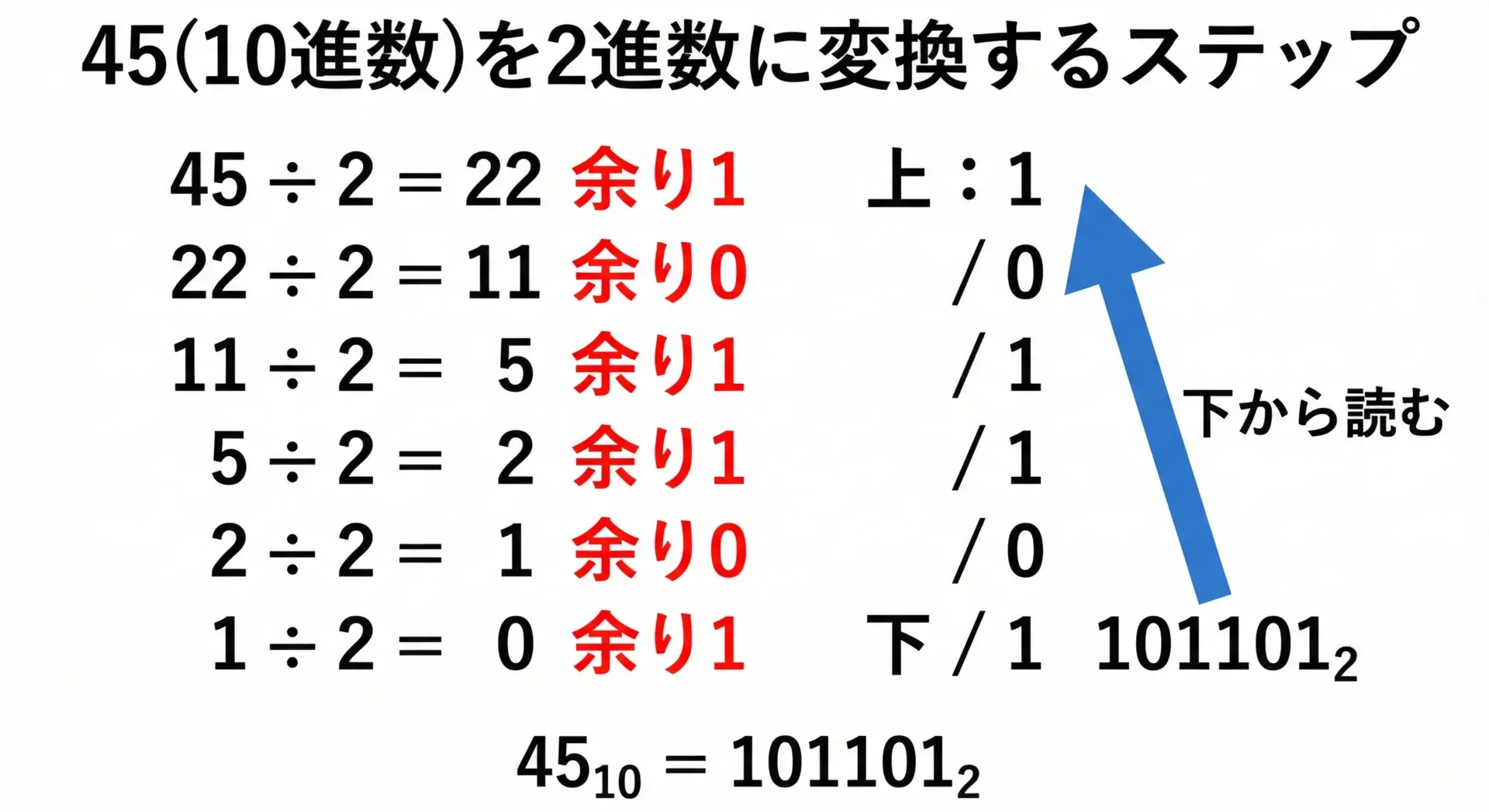
文章でまとめると次の通りです。

1. 45 ÷ 2 = 22 余り1
2. 22 ÷ 2 = 11 余り0
3. 11 ÷ 2 = 5 余り1
4. 5 ÷ 2 = 2 余り1
5. 2 ÷ 2 = 1 余り0
6. 1 ÷ 2 = 0 余り1

余りを下から上に読むと101101なので、

• 45(10進数) = 101101(2進数)

となります。

検算すると、

• 1×32(2⁵) + 0×16(2⁴) + 1×8(2³) + 1×4(2²) + 0×2(2¹) + 1×1(2⁰)
• = 32 + 0 + 8 + 4 + 0 + 1 = 45

できちんと元の数に戻ります。

2進数変換で初心者がつまずきやすいポイントと対策

2進数変換で初心者がつまずきやすいポイントはいくつかあります。

まず多いのが、余りの読み順を間違えることです。

上から読んでしまうと、ビットの順序が逆になり誤った結果になります。

これを防ぐには、「余りは必ず下から上に読む」というルールを紙に書いておく、あるいは図のように下側から矢印でなぞるクセを付けると良いでしょう。

次に、途中で割り算を間違えてしまうケースです。

特に大きな数で割り続けると、商と余りを混同することがあります。

対策としては、「商」と「余り」を列を分けて丁寧にメモすることが有効です。

最後に、先頭の0の扱いもよくある疑問です。

例えば、00101₂と101₂は同じ数を表します。

プログラミングではビット数を揃える目的で先頭に0を付けることがあるため、「値は変わらないが、表現として0を追加することがある」と理解しておくと混乱しにくくなります。

10進数から16進数へ「16で割る」変換手順

16進数の桁と記号(A〜F)の意味

16進数では、1桁が0〜15までの値を表します。

しかし、10〜15までを数字だけで表すことができないため、次のように文字を使います。

• 10 → A
• 11 → B
• 12 → C
• 13 → D
• 14 → E
• 15 → F

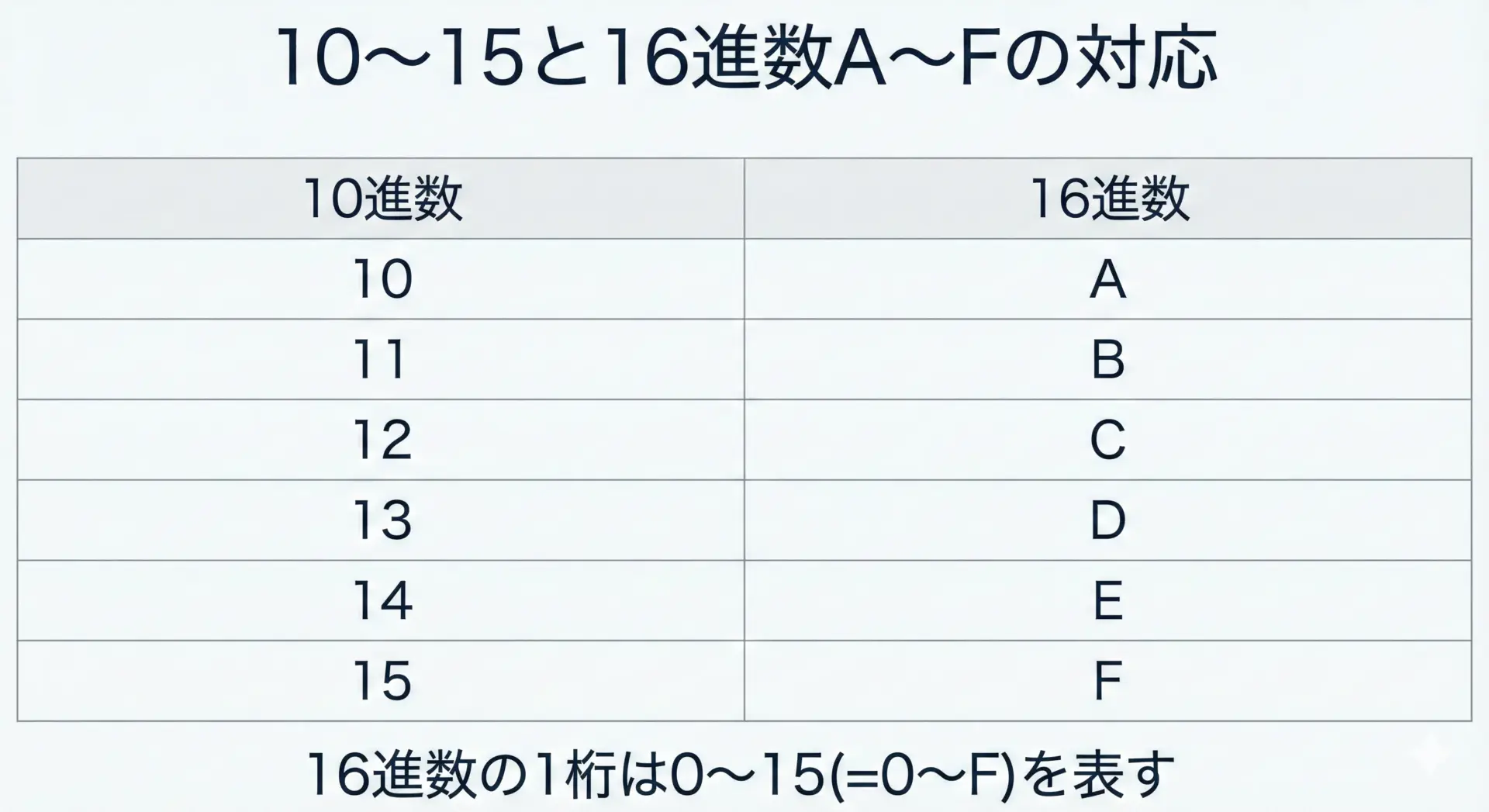
桁の重みは、10進数が10の累乗、2進数が2の累乗だったように、16進数では16の累乗になります。

例えば、16進数1Aは次のように解釈します。

• 左: 1×16¹
• 右: A(=10)×16⁰

つまり、10進数で 1×16 + 10×1 = 26 になります。

10進数を16で割り続けて16進数にする手順

基本的な手順は2進数のときとほぼ同じで、2で割る代わりに16で割るだけです。

4. 10進数Nを16で割り、商と余りを求める
5. その商をさらに16で割る
6. 商が0になるまで繰り返す
7. 出てきた余りを0〜Fに変換し、下から上に並べる

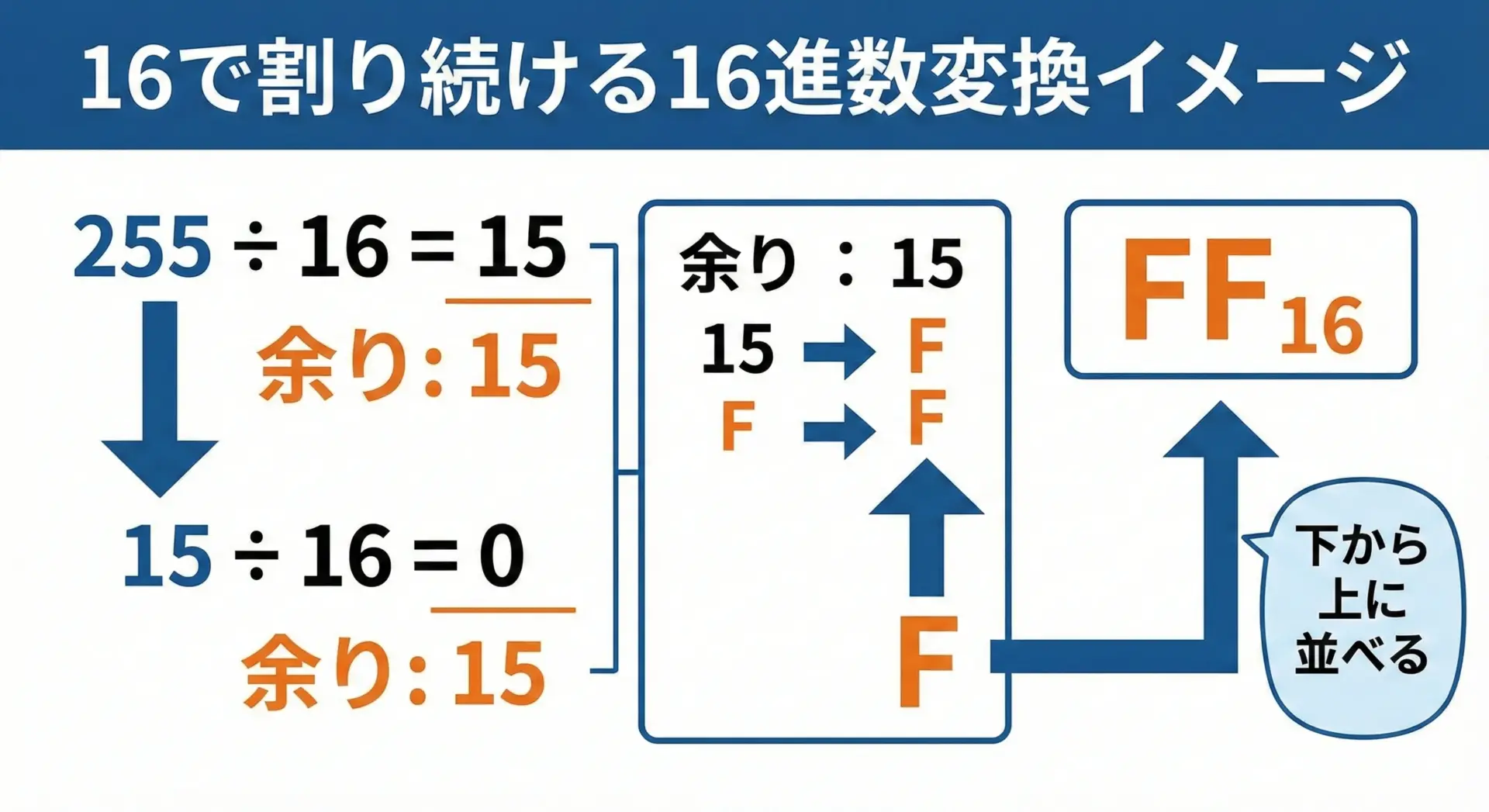
余りが10以上になった場合は、先ほどの対応表に従ってA〜Fに変換します。

余り0〜15を0〜Fに対応させる方法

余りの範囲は必ず0〜15になります。

余りの値を、そのまま16進数の1桁に対応させます。

• 0〜9 → そのまま数字0〜9
• 10〜15 → A〜F

慣れないうちは、次のような小さな表を手元に置いておくと安心です。

余りを変換 → 下から上に並べるという2ステップで、16進数表現が完成します。

具体例1(10進数255→16進数)をステップで解説

255はプログラミングでも頻出の値です。

8ビットの最大値としてよく登場します。

この255を16進数へ変換してみましょう。

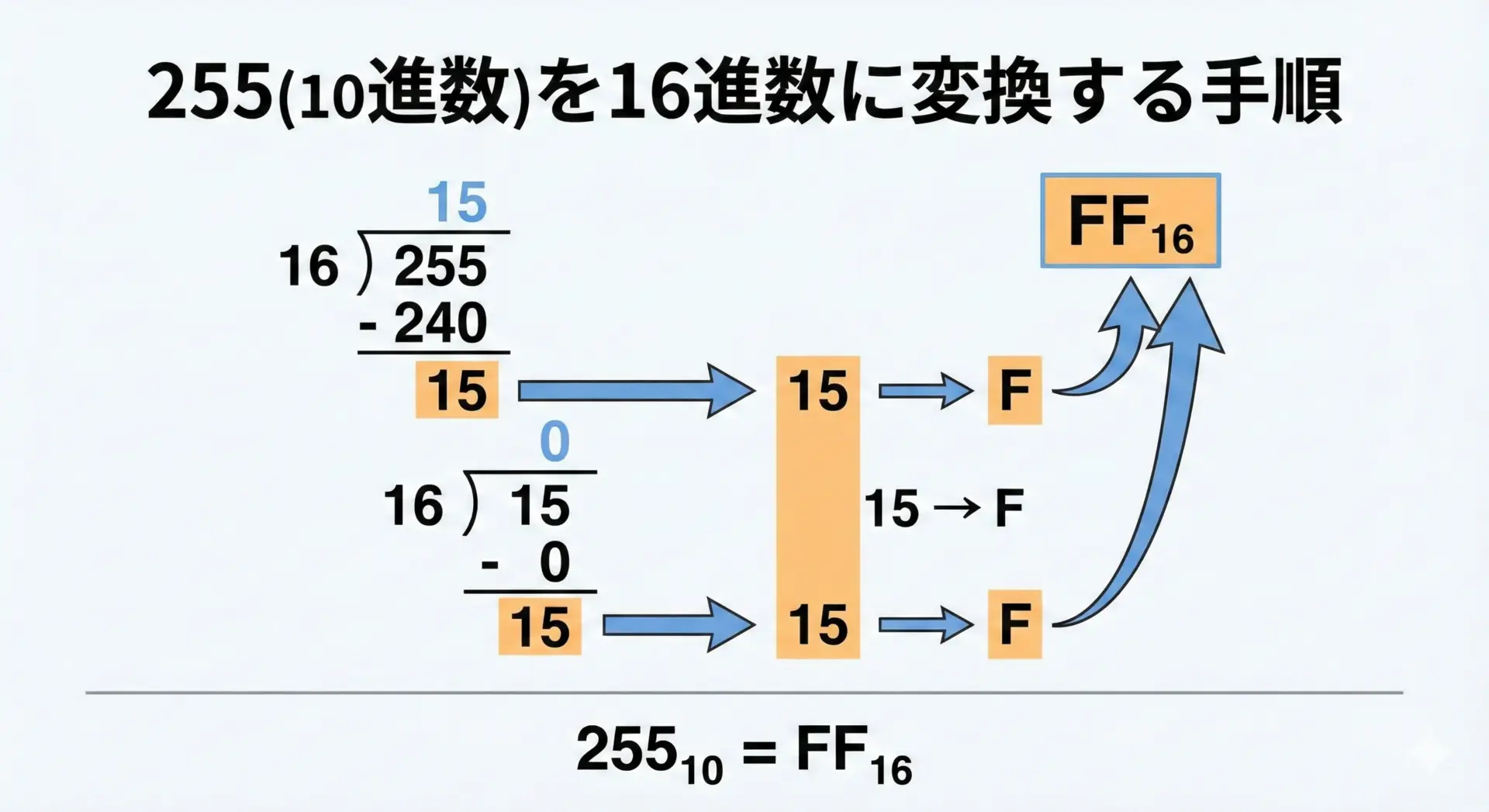
手順の詳細は次の通りです。

4. 255 ÷ 16 = 15 余り15
   → 余り15は、16進数ではF
5. 15 ÷ 16 = 0 余り15
   → 余り15は、やはりF

余りを下から上に読むとFFとなるので、

• 255(10進数) = FF(16進数)

となります。

検算してみると、

• F×16¹ + F×16⁰ = 15×16 + 15 = 240 + 15 = 255

できちんと一致します。

具体例2(少し大きな数で練習)をステップで解説

次は10進数4095を16進数に変換してみましょう。

4095は、12ビットの最大値としてよく登場します。

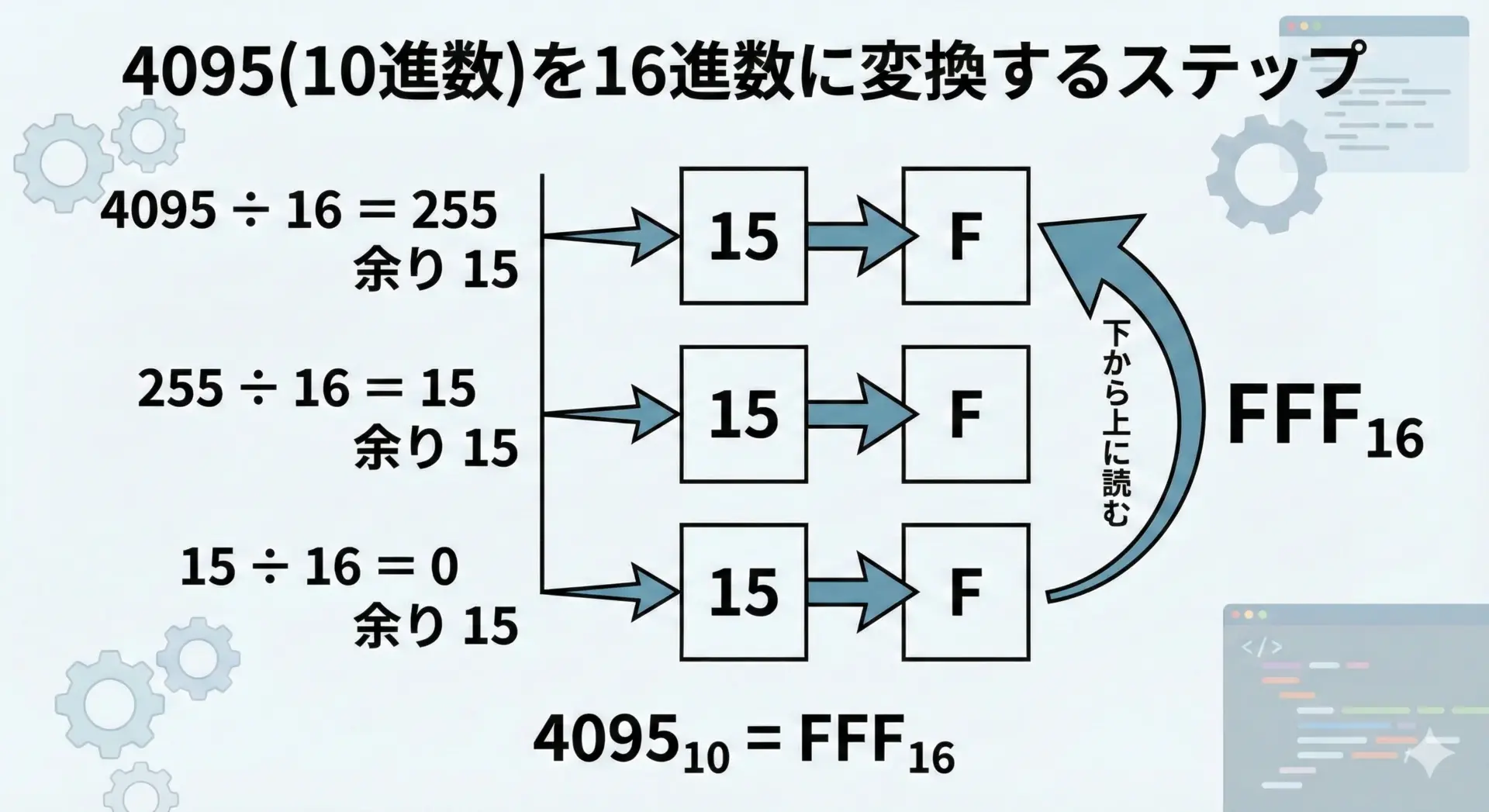
手順を整理すると、次のようになります。

4. 4095 ÷ 16 = 255 余り15 → 15 → F
5. 255 ÷ 16 = 15 余り15 → 15 → F
6. 15 ÷ 16 = 0 余り15 → 15 → F

余りを下から上に読むとFFFなので、

• 4095(10進数) = FFF(16進数)

です。

確認のために10進数に戻すと、

• F×16² + F×16¹ + F×16⁰
• = 15×256 + 15×16 + 15
• = 3840 + 240 + 15 = 4095

となり、やはり合っています。

16進数変換で混乱しないためのコツ

16進数変換で特に混乱しやすいのは、10〜15をA〜Fに変換する部分です。

ここをスムーズにするためのコツは次の2つです。

1つ目は、「10=A, 15=F」を起点にして覚えることです。

10=A、15=Fさえ覚えておけば、途中のB〜Eはアルファベット順と数字順が揃っているため、適宜数えればわかります。

2つ目は、頻出パターンを丸ごと覚えることです。

例えば、

• 255 → FF
• 4095 → FFF
• 65535 → FFFF

のような「全部F」という形は、ビット数の上限と一緒に出てきます。

このあたりを覚えておくと、デバッグ時に見かけたときに直感的に意味が分かるようになります。

2進数と16進数を「分けて」相互変換する方法

2進数4ビットと16進数1桁の対応表

2進数と16進数の大きな利点は、4ビットの2進数がちょうど16進数1桁に対応することです。

4ビットで表せるパターンは2⁴=16種類で、これは16進数の0〜Fとぴったり一致します。

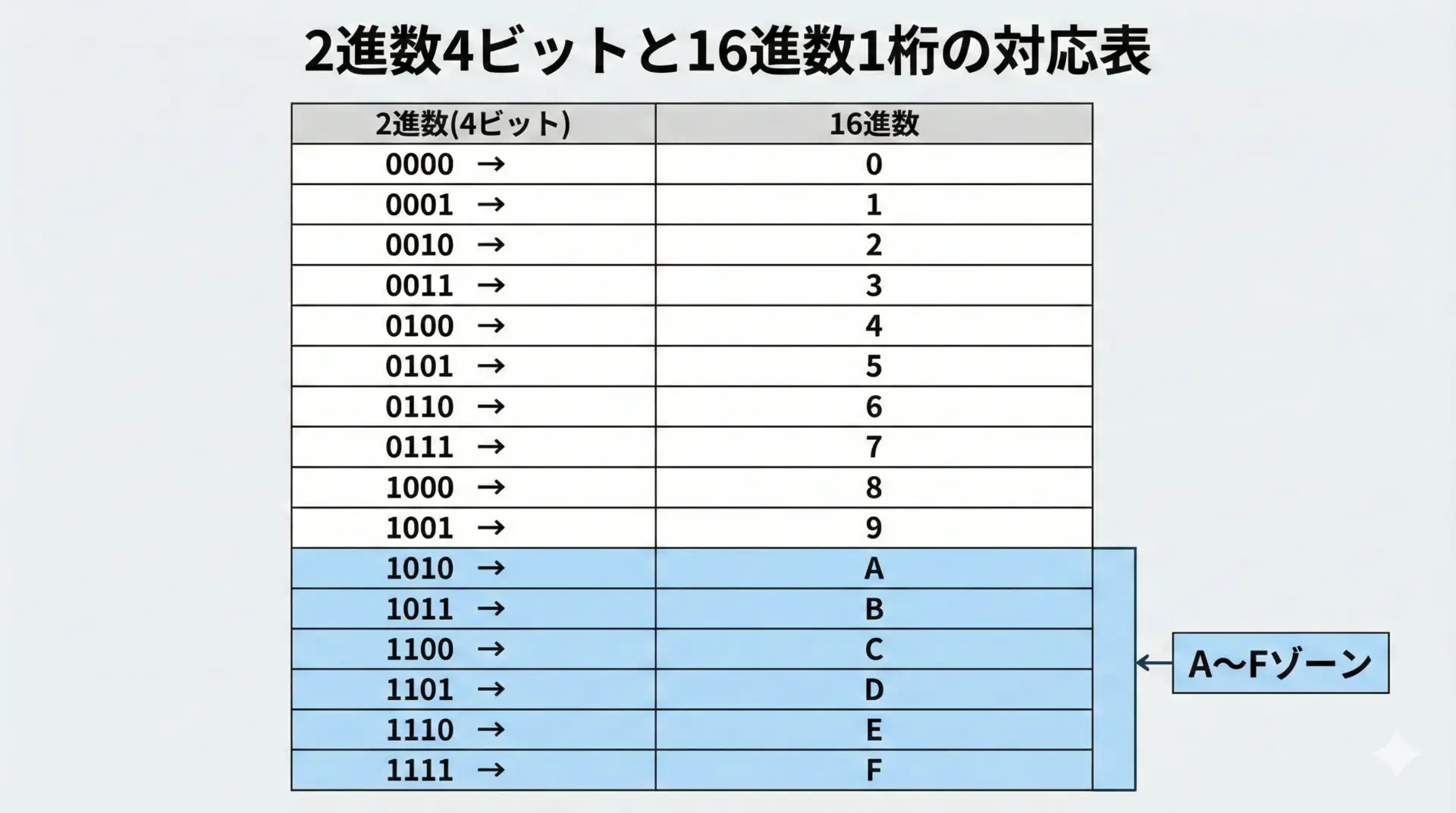
この対応表さえ頭に入れておけば、2進数と16進数の変換は「分ける」だけで行えるようになります。

2進数→16進数は「4ビットずつ分ける」だけ

2進数から16進数への変換手順は、とてもシンプルです。

4. 2進数を右から4ビットずつのグループに分ける
   (左端のグループが4ビット未満なら、先頭に0を足して4ビットにする)
5. 各4ビットを、対応表を使って16進数1桁に変換する
6. 左から順に並べる

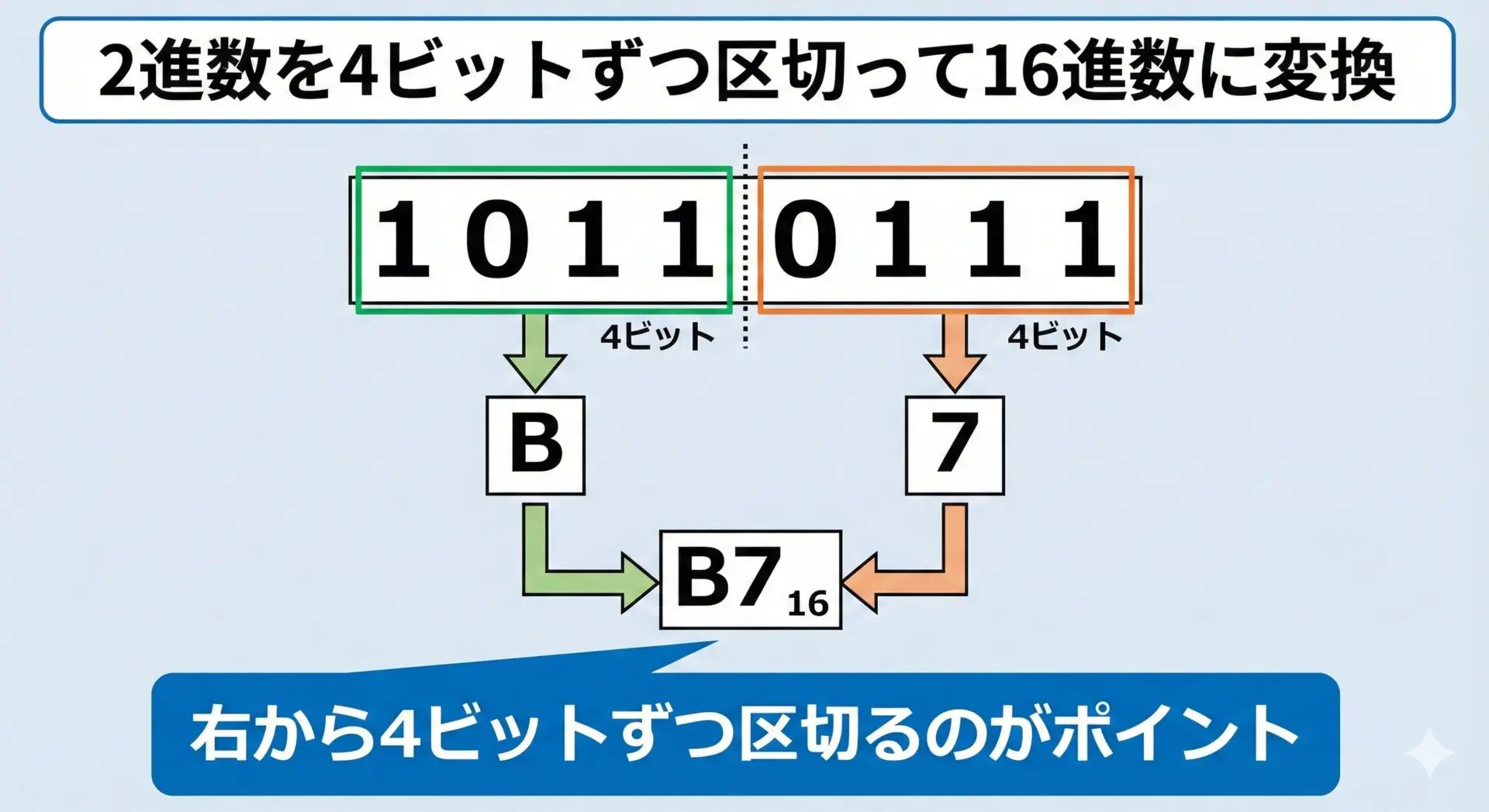
これにより、長い2進数もコンパクトな16進数にまとめることができます。

16進数→2進数は「1桁ずつ4ビットに展開」するだけ

逆に16進数から2進数へ変換する場合も、やはり対応表を使います。

4. 16進数の各桁を1文字ずつ取り出す
5. それぞれを対応する4ビットの2進数に置き換える
6. 左から順に並べる

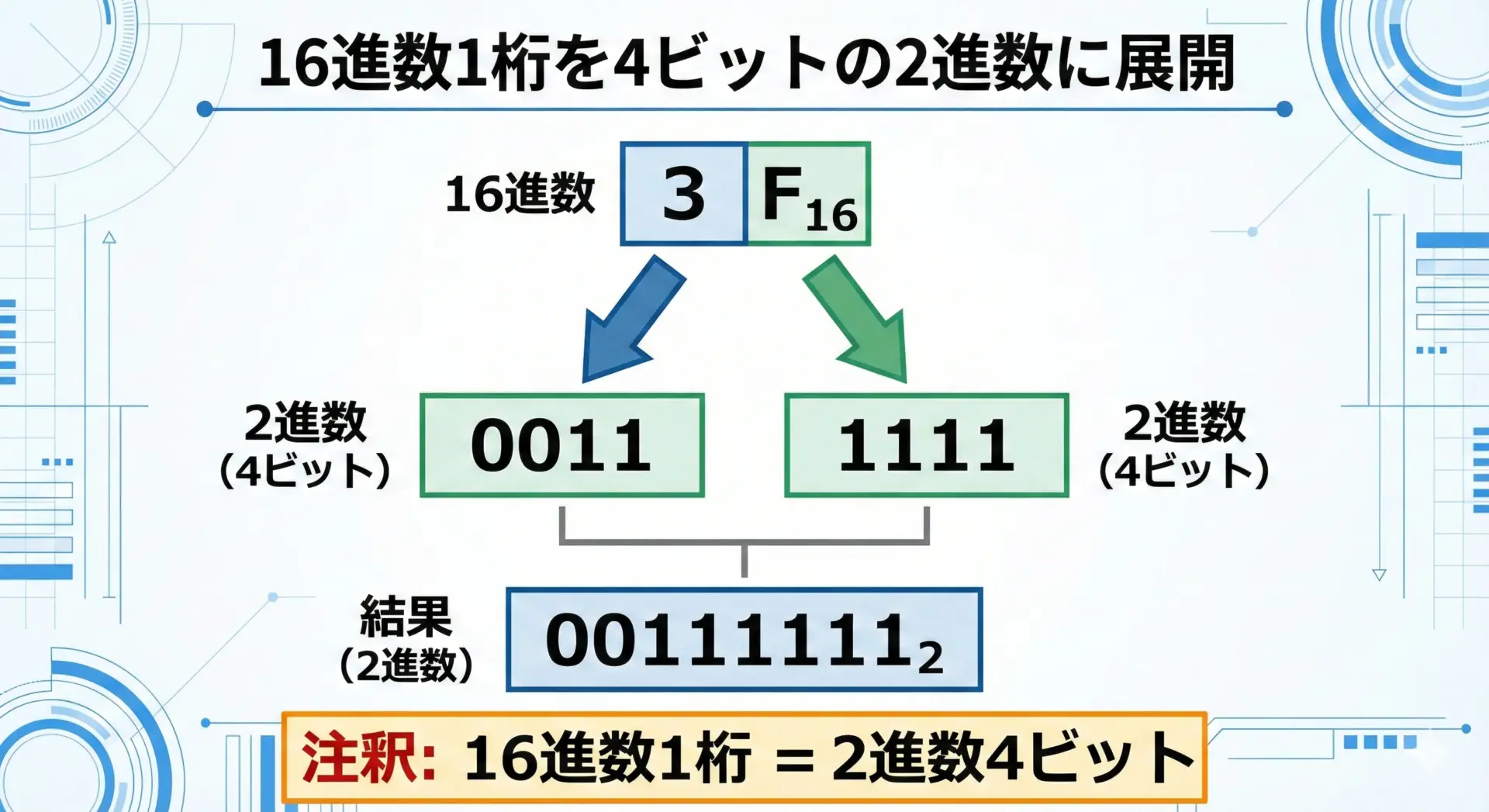
このように、16進数と2進数の間では、「4ビット」と「1桁」が常に1対1で対応しています。

具体例(2進数と16進数の相互変換)をステップで解説

ここでは、両方向の変換を1つずつやってみます。

例1: 2進数から16進数へ

2進数110101101を16進数に変換してみます。

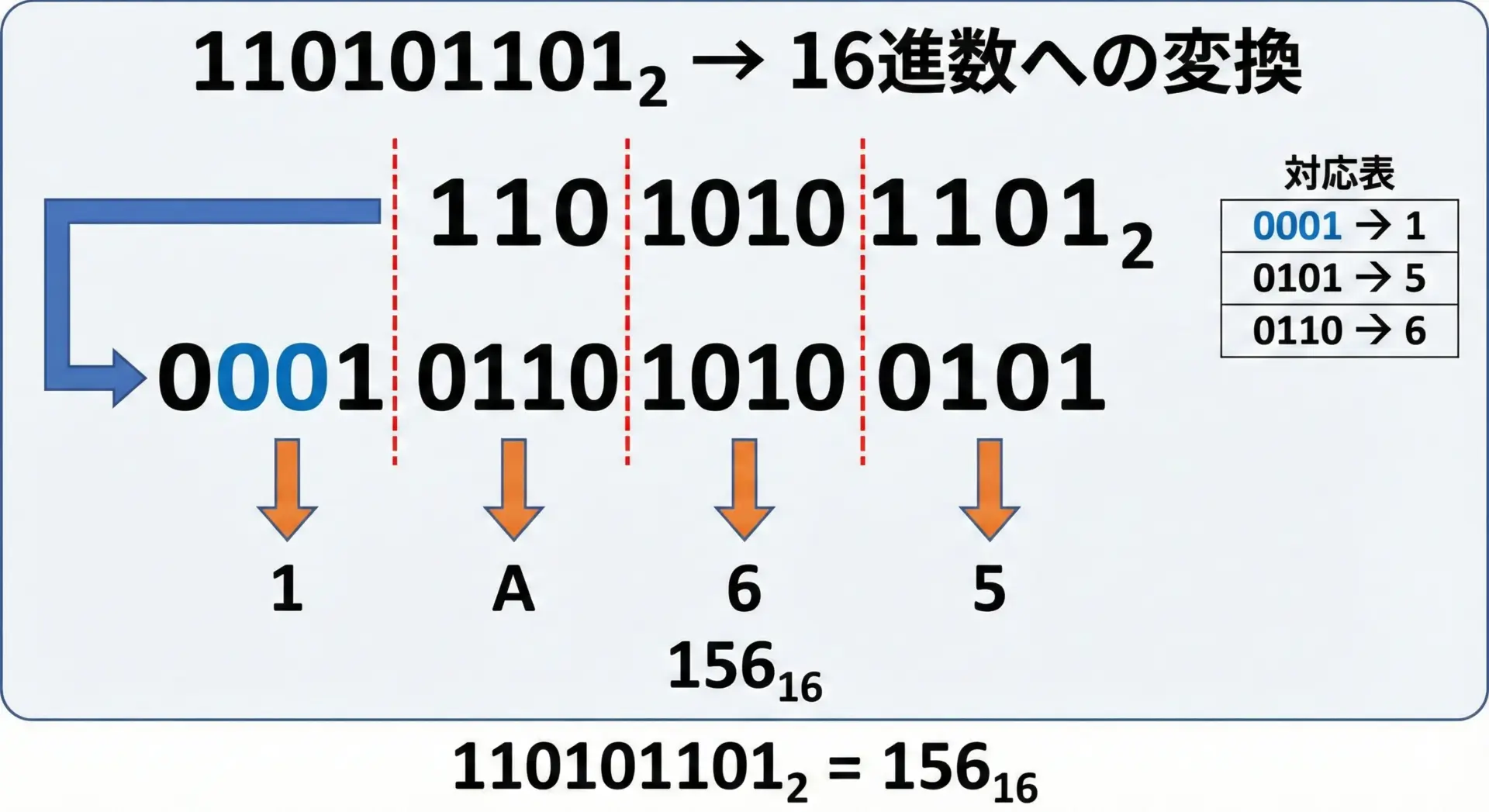
文章で整理すると次の通りです。

4. 2進数 110101101 を右から4ビットずつ区切る
   → 1 / 1010 / 1101 (見やすさのための区切り)
5. 左端が1ビットだけなので、先頭に0を3つ足して4ビットにする
   → 0001 / 0101 / 101
6. さらに右端も3ビットなので、0を1つ足して4ビットにする
   → 0001 / 0101 / 1101
7. 対応表から変換
   4. 0001 → 1
   5. 0101 → 5
   6. 1101 → D
8. 左から並べて
   4. 110101101₂ = 15D₁₆

(ここでは最終的な区切りを「0001 0101 1101」と解釈し、結果として15D₁₆になります)

例2: 16進数から2進数へ

次に、16進数2AFを2進数にしてみましょう。

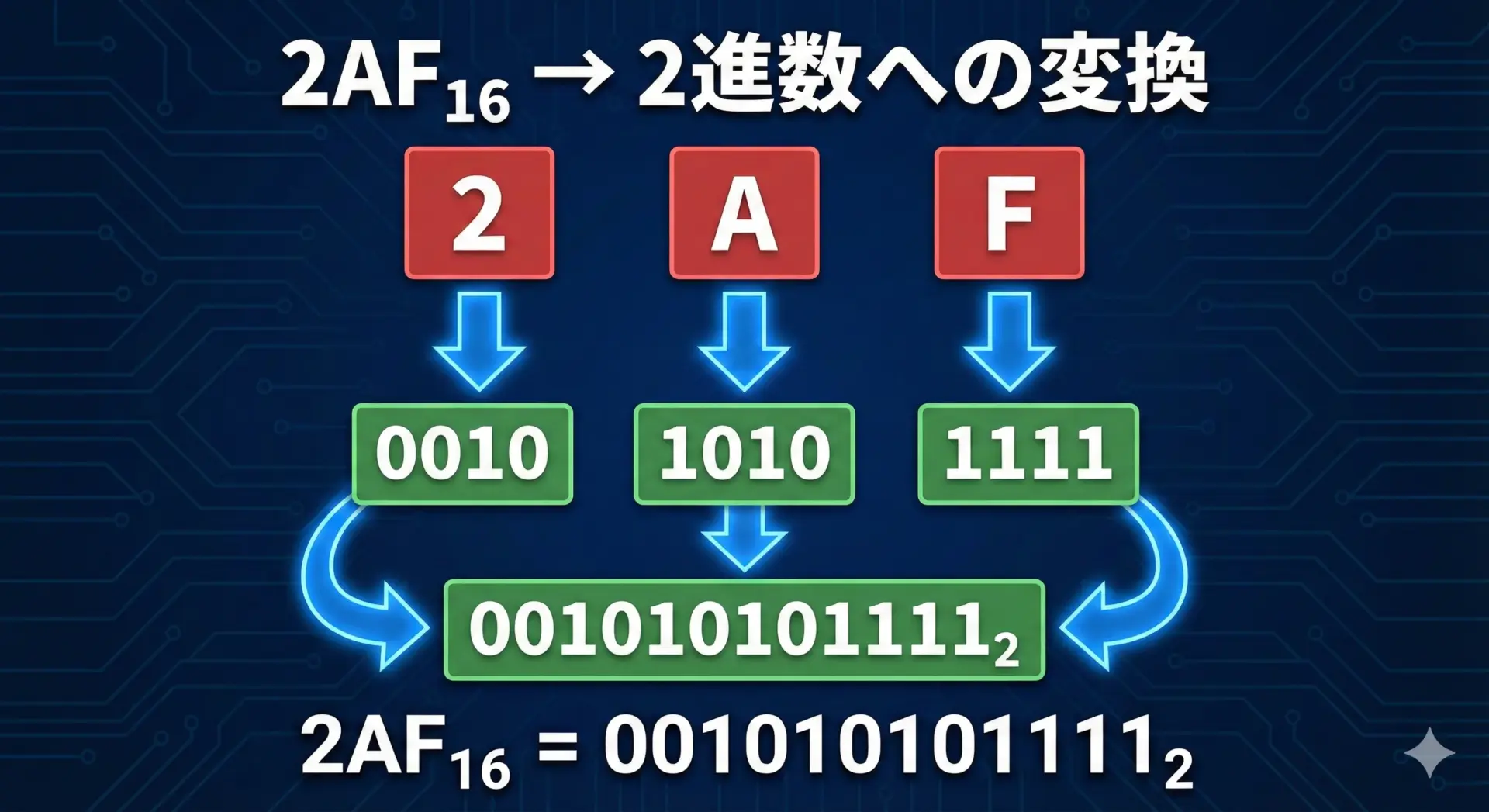
文章で整理するとこうなります。

4. 各桁を調べる
   4. 2 → 2進数で 0010
   5. A(=10) → 2進数で 1010
   6. F(=15) → 2進数で 1111
5. それらを左から順に並べる
   →2AF₁₆ = 0010 1010 1111₂

先頭の0は省いても値は変わらないので、1010101111₂と書いても構いません。

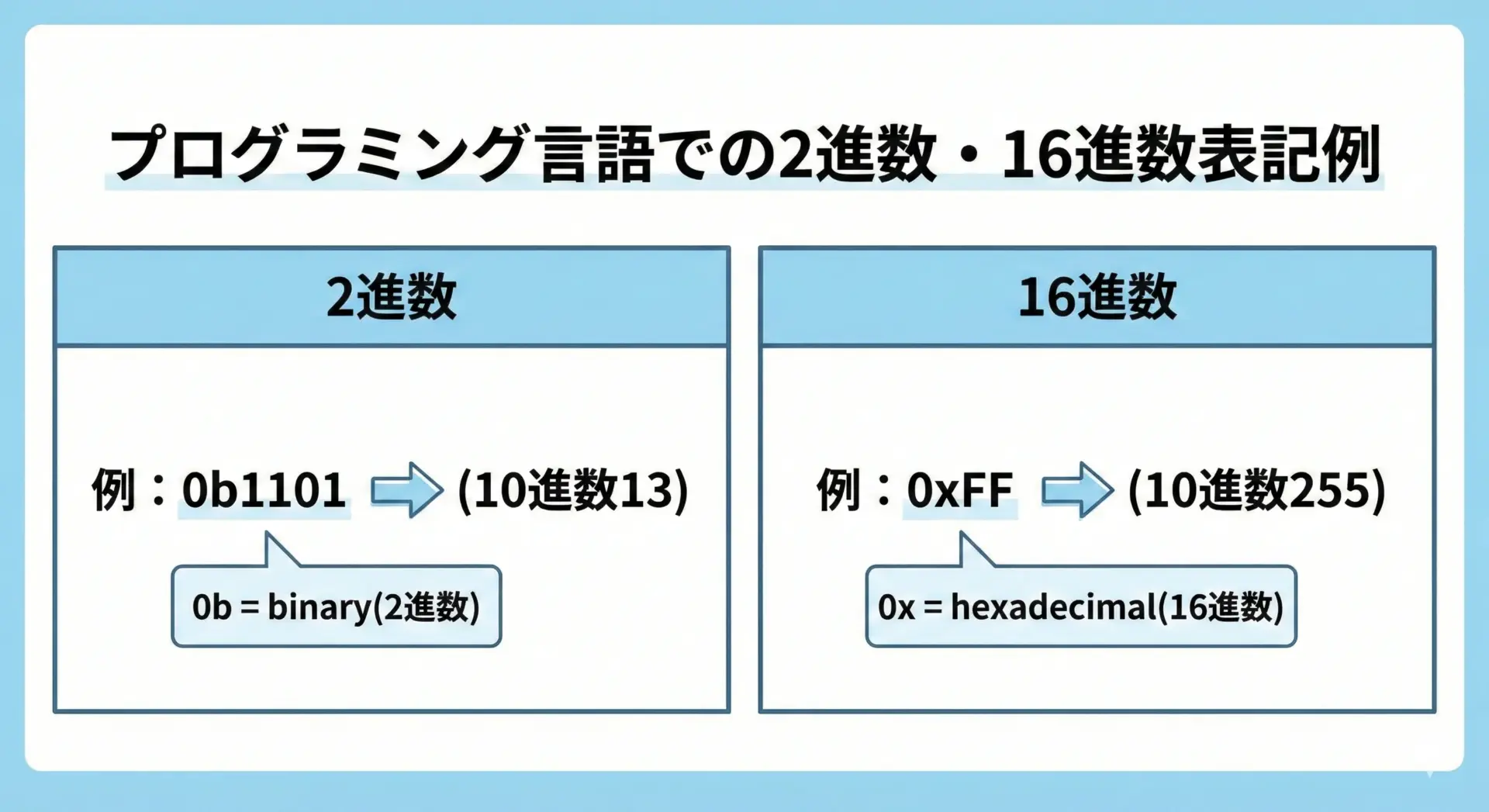
プログラミングでの2進数・16進数表記(0b, 0x)と変換の活用

多くのプログラミング言語では、数値リテラルに接頭辞を付けることで、2進数や16進数を直接書くことができます。

代表的な例を挙げると、次のようになります。

• 2進数リテラル
  • C系言語(C, C++, Java, JavaScriptなど): 0b1010
  • Python: 0b1010
• 16進数リテラル
  • C系言語: 0xFF
  • Python: 0xFF

また、言語によっては標準ライブラリで簡単に変換する関数も用意されています。

Pythonの例を挙げると、

n = 13
bin_str = bin(n)  # '0b1101'
hex_str = hex(n)  # '0xd'

のように、bin()やhex()を使うと、10進数から2進数・16進数への文字列表現が簡単に得られます。

自分で「割る」「分ける」の手順を理解しておくと、ライブラリの結果を頭の中で検算できるようになり、バグの原因を追いやすくなります。

ビット演算やフラグ管理のコードを読む際にも、1ビットずつの意味をイメージしやすくなるでしょう。

まとめ

本記事では、10進数から2進数・16進数への変換と、2進数と16進数の相互変換について、「割る」「分ける」という2つの操作に注目して解説しました。

• 10進数 → 2進数
  2で割り続けて余り(0か1)を下から上に読むことで、ビット列が得られます。
• 10進数 → 16進数
  16で割り続けて余り(0〜15)を0〜Fに対応させ、同じく下から上に並べます。
• 2進数 ↔ 16進数
  2進数4ビットと16進数1桁が1対1に対応するため、4ビットずつ分ける / 1桁ずつ4ビットに展開するだけで相互変換できます。

これらの手順を手計算で一度じっくり追いかけてみると、プログラミング言語が提供する0bや0xといった表記の意味が腑に落ちやすくなります。

特に、ビット演算やフラグ管理、メモリアドレスやカラコードの扱いなど、実務で頻出する場面で役立つ知識です。

「難しい公式ではなく、2で割る・16で割る・4ビットで分ける」という視点を持つことで、基数変換はぐっと身近なものになります。

ぜひ、自分の手でいくつかの数を変換してみて、身体で覚えてみてください。