C++では演算子オーバーロードを使うことで、自作クラスに直感的で読みやすい「演算子らしい」書き方を与えることができます。
本記事では、基本ルールから代表的な書き方、注意点、実用的なサンプルコードまでを、図解を交えながら詳しく解説します。
数値クラスやベクトルクラスなどを作る予定がある方は、ぜひ最後まで読んでみてください。
C++の演算子オーバーロードとは
演算子オーバーロードのイメージ

演算子オーバーロードとは、演算子を「関数」として定義し直す機能のことです。
たとえば、自作のVector2Dクラスに+演算子を定義すれば、次のような直感的なコードが書けます。
Vector2D a(1.0, 2.0);
Vector2D b(3.0, 4.0);
// 演算子オーバーロードを行うことで、数値型と同じような書き方ができる
Vector2D c = a + b;内部的にはa.operator+(b)またはoperator+(a, b)という関数呼び出しに展開されます。
つまり演算子オーバーロードは「シンタックスシュガー(糖衣構文)」であり、実態は関数呼び出しです。
演算子オーバーロードの基本ルール
オーバーロードできる演算子・できない演算子
C++では、ほとんどの演算子をオーバーロードできますが、一部は禁止されています。
代表的なものを表で整理します。
| 種類 | 代表例 | オーバーロード可否 | 補足 |
|---|---|---|---|
| 算術 | + - * / % | 可能 | 2項・単項どちらも可能 |
| 比較 | == != < <= > >= | 可能 | C++20では3-way比較(<=>)も便利 |
| 代入系 | = += など | 可能 | コピー・ムーブ代入もここに含まれる |
| インクリメント | ++ -- | 可能 | 前置・後置を区別して定義が必要 |
| 添字 | [] | 可能 | コンテナ風クラスで多用される |
| 関数呼び出し | () | 可能 | 関数オブジェクト(ファンクタ)で利用 |
| メンバーアクセス | -> * | 可能 | スマートポインタなどの実装に |
| ストリーム | << >> | 可能 | std::cout や std::cin との連携に |
| 論理演算 | && || ! | 可能 | ただし短絡評価は再現不可 |
| メモリ管理 | new delete | 可能 | カスタムアロケータの実装などに |
| オーバーロード不可 | ?: . :: sizeof など | 不可 | 言語仕様として禁止されている |
演算子そのものの「意味」を完全に変えることはできません。
たとえば+は足し算・結合のイメージで使うべきであり、まったく別の動作をさせると可読性が著しく低下します。
演算子オーバーロードの書き方パターン
演算子オーバーロードには、主に次の2パターンがあります。
- メンバー関数として定義する
- 非メンバー(フリー関数)として定義する
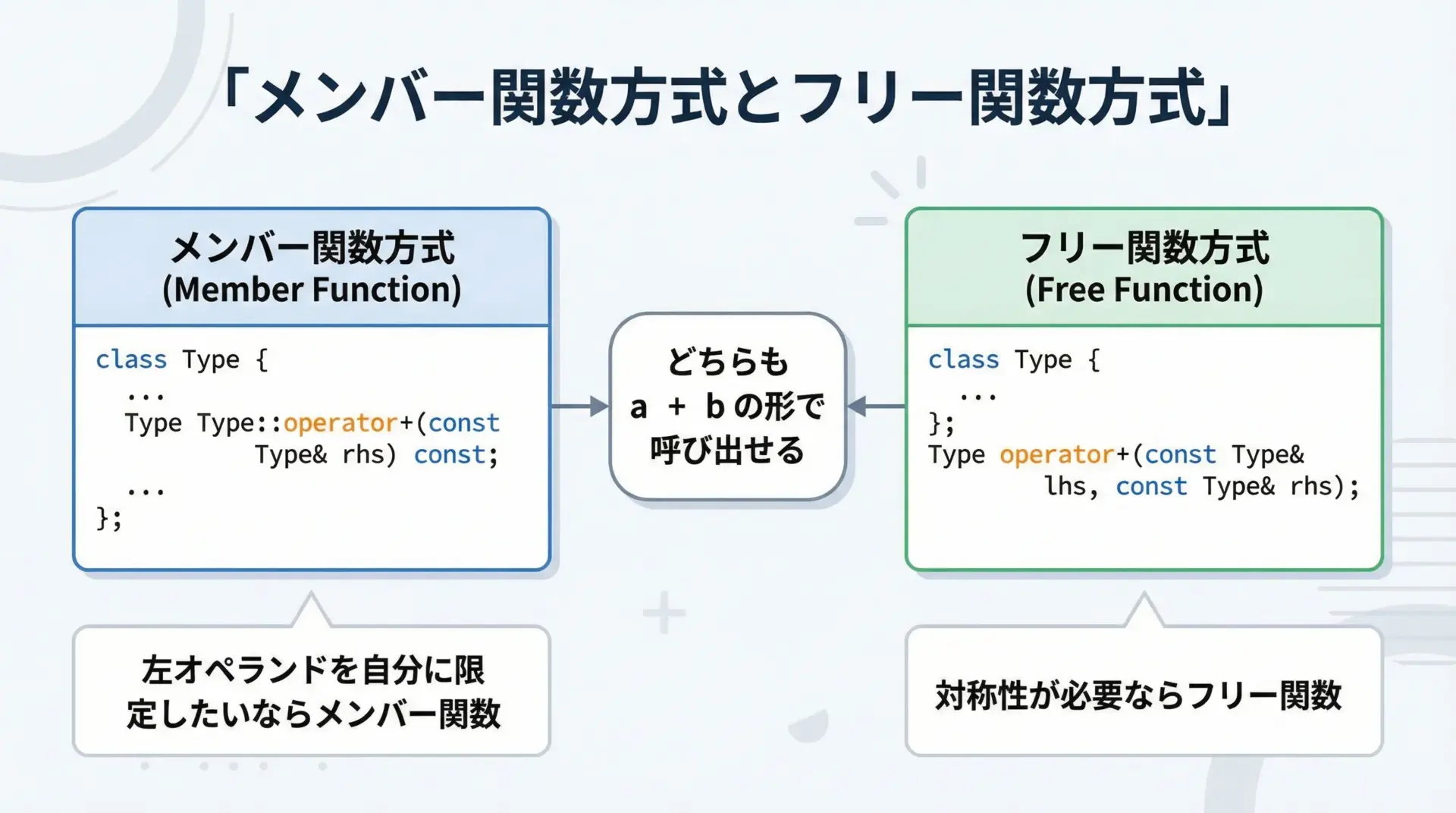
どちらの書き方でもa + bという式で呼び出せますが、設計上の向き不向きがあります。
これについては後述の実例で詳しく見ていきます。
実例で学ぶ: ベクトルクラスの演算子オーバーロード
ここでは、2次元ベクトルVector2クラスを題材に、代表的な演算子オーバーロードを順に実装していきます。
Vector2クラスの定義
まずは、基本的なクラス定義です。
#include <iostream>
// 2次元ベクトルを表すクラス
class Vector2 {
public:
double x;
double y;
// コンストラクタ
Vector2(double x_ = 0.0, double y_ = 0.0)
: x(x_), y(y_) {}
};ここに、加算・減算・スカラー倍などの演算子を追加していきます。
2項演算子+と-のオーバーロード
メンバー関数として定義する例
左辺が必ずVector2になることが前提でよい場合は、メンバー関数として実装すると分かりやすくなります。
class Vector2 {
public:
double x;
double y;
Vector2(double x_ = 0.0, double y_ = 0.0)
: x(x_), y(y_) {}
// ベクトル同士の加算 (a + b)
Vector2 operator+(const Vector2& rhs) const {
// ここで新しいVector2を作って返す
return Vector2(this->x + rhs.x, this->y + rhs.y);
}
// ベクトル同士の減算 (a - b)
Vector2 operator-(const Vector2& rhs) const {
return Vector2(this->x - rhs.x, this->y - rhs.y);
}
};constを付けているのは、演算によって自分自身の状態を変えないことを保証するためです。
加算・減算は「新しい値を作る」イメージなので、このように実装すると自然です。
単項演算子-のオーバーロード
符号反転も、演算子オーバーロードで書けます。
class Vector2 {
// ... (略)
// 単項マイナス (-a)
Vector2 operator-() const {
return Vector2(-x, -y);
}
};これによりVector2 v(1, 2);に対して-vと書けるようになります。
スカラー倍*のオーバーロード
スカラー倍には、左辺がVector2の場合(v * 2.0)と、左辺がスカラーの場合(2.0 * v)の2パターンがあります。
左辺がVector2の場合(メンバー関数)
class Vector2 {
// ... (略)
// ベクトル * スカラー (v * s)
Vector2 operator*(double s) const {
return Vector2(x * s, y * s);
}
};この定義だけだとv * 2.0は動きますが、2.0 * vはコンパイルエラーになります。
なぜなら、2.0はdoubleであり、double型のメンバー関数としてoperator*(Vector2)を定義することはできないからです。
左辺がスカラーの場合(非メンバー関数)
対称性を保つために、フリー関数としてoperator*を定義します。
// ベクトル * スカラー (メンバー関数で定義済み)
// Vector2 Vector2::operator*(double s) const;
// スカラー * ベクトル (2.0 * v) をサポートするフリー関数
Vector2 operator*(double s, const Vector2& v) {
// 実装は v * s に委譲してもよい
return v * s;
}このように、左右のオペランドに対して公平な演算を行う場合はフリー関数を利用するのが定石です。
比較演算子==と!=
ベクトル同士を比較したい場合は、==と!=をオーバーロードします。
対称性が重要なので、フリー関数として実装するのが自然です。
class Vector2 {
public:
double x;
double y;
Vector2(double x_ = 0.0, double y_ = 0.0)
: x(x_), y(y_) {}
};
// ベクトル同士の等価比較 (a == b)
bool operator==(const Vector2& lhs, const Vector2& rhs) {
return lhs.x == rhs.x && lhs.y == rhs.y;
}
// ベクトル同士の非等価比較 (a != b)
bool operator!=(const Vector2& lhs, const Vector2& rhs) {
return !(lhs == rhs); // == に処理を委譲
}浮動小数点を扱う場合は、完全一致比較は誤差の問題で危険です。
実際のアプリケーションでは、「許容誤差以内なら等しい」とみなす比較関数を別途用意することが一般的です。
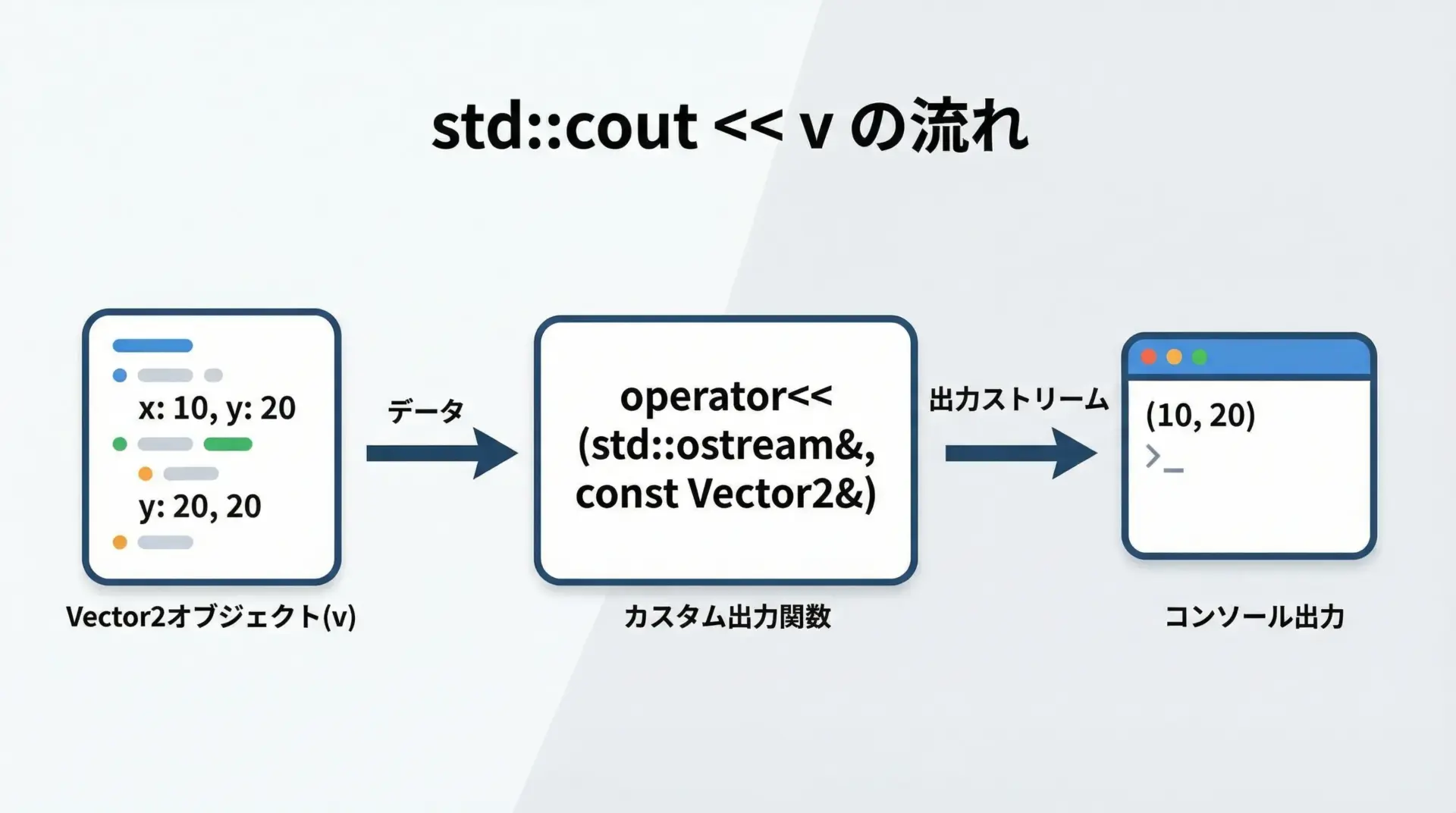
ストリーム演算子<<による出力
標準出力やログに自作クラスの内容をきれいに表示したいときに、多用されるのがoperator<<のオーバーロードです。
#include <iostream>
class Vector2 {
public:
double x;
double y;
Vector2(double x_ = 0.0, double y_ = 0.0)
: x(x_), y(y_) {}
};
// 出力用の演算子オーバーロード
std::ostream& operator<<(std::ostream& os, const Vector2& v) {
// 好きな形式で出力形式を決められる
os << "(" << v.x << ", " << v.y << ")";
return os; // 連結 (cout << v1 << v2;) を可能にするため参照を返す
}
int main() {
Vector2 a(1.0, 2.0);
Vector2 b(3.5, -1.2);
std::cout << "a = " << a << std::endl;
std::cout << "b = " << b << std::endl;
std::cout << "a + b = " << (a + b) << std::endl;
}a = (1, 2)
b = (3.5, -1.2)
a + b = (4.5, 0.8)戻り値をstd::ostream&にすることで、出力のチェーンを自然に書けるようになります。
この書き方は、すべてのストリーム演算子オーバーロードでほぼ共通です。
インクリメント/デクリメントの前置・後置オーバーロード
インクリメント++とデクリメント--は、前置と後置でシグネチャが異なる点に注意が必要です。
ここでは、簡単な整数ラッパークラスで確認します。
前置++iの定義
class Counter {
int value;
public:
Counter(int v = 0) : value(v) {}
// 前置インクリメント (++i)
Counter& operator++() {
++value; // まず自分をインクリメント
return *this; // その結果の参照を返す
}
int get() const { return value; }
};前置++は「自分を進めてから返す」動作を、自分自身への参照を返すことで表現します。
後置i++の定義
後置インクリメントは、「ダミーのintパラメータ」をシグネチャに付けることで表現します。
class Counter {
int value;
public:
Counter(int v = 0) : value(v) {}
// 前置インクリメント (++i)
Counter& operator++() {
++value;
return *this;
}
// 後置インクリメント (i++)
Counter operator++(int) {
Counter old(*this); // 変更前の状態を保存
++value; // 自分をインクリメント
return old; // 変更前の値を返す
}
int get() const { return value; }
};
int main() {
Counter c(5);
Counter a = ++c; // 前置: cは6になり、aも6
Counter b = c++; // 後置: cは7になるが、bは6(インクリメント前の値)
std::cout << "c = " << c.get() << std::endl;
std::cout << "a = " << a.get() << std::endl;
std::cout << "b = " << b.get() << std::endl;
}c = 7
a = 6
b = 6後置演算子は、一時オブジェクトのコピーを伴うため前置よりもコストが高くなる傾向があります。
ループなどの多用箇所では++iを使うのが慣習です。
演算子オーバーロードの設計・実装の注意点
1. 直感に反する挙動を避ける
「読み手が普通に想像する動作」から外れないことが最重要です。
+は加算・結合の意味で使う-は減算・差分の意味で使う==は「同じものか」の判定に使う
たとえばoperator+でファイルを消去したり、operator==でログを書き込んだり、といった副作用の大きい処理を入れるのは避けるべきです。
2. 値を変える演算子は非const、変えない演算子はconst
オブジェクトの状態を変えるかどうかを、const修飾で区別することが大切です。
operator+()やoperator-()など「新しい値を返すだけ」の演算子はconstにするoperator+=()やoperator++()など「自分を更新する」演算子はconstにしない
この区別を守ることで、コードの意図が明確になり、誤用も防ぎやすくなります。
3. 対称性が必要な場合はフリー関数で実装
左右どちらも同じように扱いたい演算(加算・比較・スカラー倍など)は、可能な限りフリー関数で実装し、必要に応じてfriend指定でプライベートメンバーにアクセスさせる、というスタイルがよく用いられます。
class Vector2 {
double x;
double y;
public:
Vector2(double x_ = 0.0, double y_ = 0.0)
: x(x_), y(y_) {}
// フリー関数からプライベートメンバーにアクセスできるようにする
friend Vector2 operator+(const Vector2& lhs, const Vector2& rhs);
};
// フリー関数としてoperator+を定義
Vector2 operator+(const Vector2& lhs, const Vector2& rhs) {
return Vector2(lhs.x + rhs.x, lhs.y + rhs.y);
}クラスのインターフェースをすっきり保ちつつ、対称な演算を提供できるため、数値系クラスではよく見られるパターンです。
4. パフォーマンスを意識した参照・戻り値設計
- 引数は「原則として
const&で受ける」と、コピーのコストを抑えられます。 - 戻り値は、新しい値を返す演算子は値返し、自分を更新する演算子は自分への参照を返すと覚えると整理しやすくなります。
例:
// a + b は新しい値を返す: 値で返す
Vector2 operator+(const Vector2& lhs, const Vector2& rhs);
// a += b は自分を更新して自分を返す: 参照で返す
Vector2& operator+=(Vector2& lhs, const Vector2& rhs);まとめ
演算子オーバーロードは、C++で自作クラスを「組み込み型と同じような感覚」で扱えるようにする強力な機能です。
本記事では、Vector2クラスを例に+や-、スカラー倍、比較、ストリーム出力、インクリメント演算子などを実装しながら、メンバー関数/フリー関数の使い分けや、前置・後置の違い、設計上の注意点を整理しました。
実際の開発では、「直感に合う動作か」「constの付け方は適切か」「コピーコストは問題ないか」を意識しながら、必要な演算子だけを慎重にオーバーロードしていくことが重要です。

