プログラミングを学び始めると、多くの人が「数学が苦手だけど大丈夫だろうか」と不安を感じます。
一方で、「エンジニアになるには高度な数学が必須」というイメージも根強くあります。
本記事では、プログラミングに数学はどこまで必要なのかを整理しながら、「あまり数学を使わないケース」と「確実に数学が必要になる分野」を具体的に解説します。
プログラミングに数学は必要か?結論から整理
結論として、一般的なWebサービス開発や業務システム開発であれば、高度な数学はほとんど必要ありません。
ただし、分野によっては大学レベル以上の数学が「ほぼ必須」になります。
ここで大事なのは、「プログラミング」と一口に言っても、扱う分野や役割が大きく異なるという点です。
フロントエンド、バックエンド、業務アプリ、ゲーム、AI、データ分析など、それぞれで求められる数学のレベルも変わります。
「日常的な開発」と「専門分野」で分けて考える
プログラミングと数学の関係を理解しやすくするために、まずはざっくりと次の2つに分けてみます。
- 日常的な業務システムやWebアプリなど、ビジネス寄りの開発
- アルゴリズムや物理演算、機械学習など、数理モデルを多用する専門分野の開発
前者は中学〜高校レベルの数学(四則演算、割合、簡単な関数やグラフ)で十分なことが大半です。
後者は、線形代数や確率論、微積分など、大学以降の数学知識があると初めて本格的に取り組める世界です。
数学がほとんど不要なプログラミング分野
「数学ができないからプログラミングは無理」と考えるのは早計です。
実務の現場では、複雑な数式を扱わない仕事も数多く存在します。
1. Web制作・フロントエンドの基本部分
Webサイトの表示やユーザーインターフェースを作るフロントエンド開発では、デザインとユーザビリティが重視されることが多く、高度な数学を使う場面はほとんどありません。
HTMLやCSS、JavaScriptを用いて、画面のレイアウトを調整したり、ボタンを押したときの動きを実装したりする段階では、必要になるのは次のようなレベルです。
- 足し算・引き算・掛け算・割り算
- ピクセル数やパーセンテージによるレイアウト調整
- 簡単な条件分岐や繰り返しのロジック
例えば、ウィンドウの幅に応じてコンテンツの幅を50%にする、スクロール量によってアニメーションを開始する、といった処理は、四則演算と比較で十分対応可能です。
2. 一般的な業務システム・CRUDアプリ
いわゆる「業務システム」や「管理画面」「社内ツール」などの開発も、数学よりは業務知識と設計力の比重が大きい分野です。
ここでよく登場するのは次のような処理です。
- 顧客情報の登録・更新・削除(CRUD処理)
- 売上の集計や簡単な統計(合計・平均・最大・最小)
- 日付や時間の計算(締め日、期間フィルタなど)
これらは、算数レベルの計算とロジカルシンキングができれば実装可能であり、微分方程式や線形代数を駆使するような場面はまずありません。
3. ノーコード / ローコード開発
近年増えているノーコード・ローコードツールを用いた開発は、そもそもプログラミング言語のコードを書く場面が少なく、数学的な負荷も一層小さくなります。
ただし、画面遷移やデータの流れを設計したり、条件分岐や集計のロジックを考えたりする場面は多いため、「論理的に物事を分解する力」は求められます。
これは机上の数学というより、日常的な思考力に近いスキルです。
数学が重要になるプログラミング分野
一方で、「数学ができないと厳しい」と言わざるを得ない分野も確かに存在します。
ここでは代表的な領域を取り上げます。
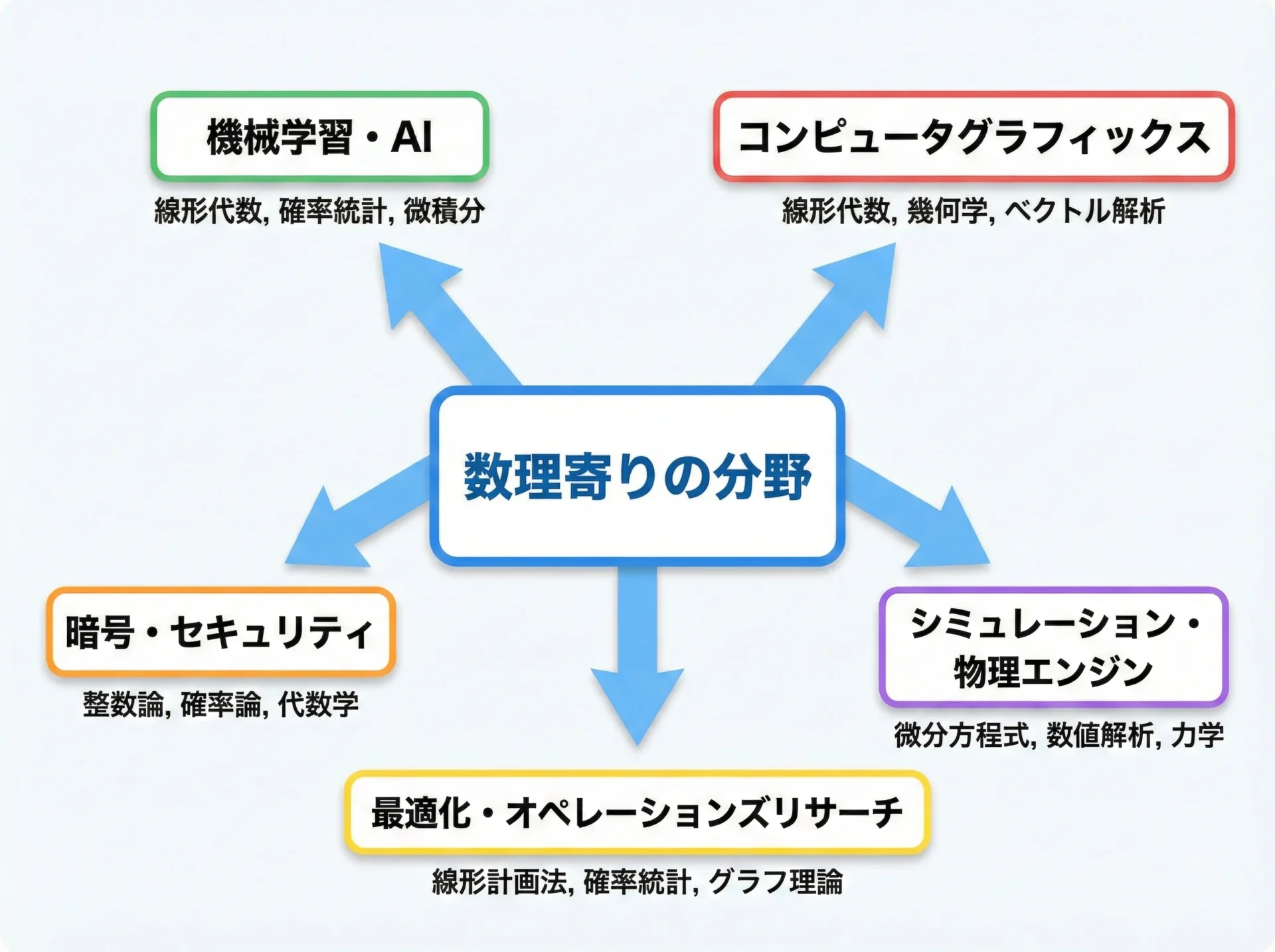
図で示したような分野では、数学がコードそのものに深く埋め込まれているため、数式を理解できるかどうかがそのまま実装力に直結します。
1. 機械学習・AI・データサイエンス
機械学習やAIの領域では、線形代数・確率統計・微積分が頻繁に登場します。
たとえば次のような場面です。
- ニューラルネットワークの重み更新(勾配降下法における微分)
- 回帰分析・分類問題における損失関数と最適化
- ベイズ推定や信頼区間など、統計的な解釈を要する分析
ライブラリscikit-learnやTensorFlowを呼び出すだけであれば、数式を細部まで理解していなくても動かすこと自体は可能です。
しかし、パラメータを適切に調整し、結果を正しく解釈し、モデルの改善案を考えるとなると、数学の理解がないと限界が早く訪れます。
2. コンピュータグラフィックス・ゲーム開発の一部
ゲーム開発全体で見ると、UI実装やステージ設計など数学をあまり使わない部分も多いものの、3D表現や物理演算を扱う部分は数学の塊です。
典型的には次のような知識が関連します。
- ベクトル・行列による座標変換(線形代数)
- 物体の運動や衝突判定(力学・微分方程式)
- 光源処理やシェーダー(線形代数・解析)
例えば、3D空間でオブジェクトを回転させる処理は、回転行列やクォータニオンを用いて座標を変換する操作です。
数学をブラックボックスにすることも可能ですが、チューニングや高度な表現を行うには数理の理解が欠かせません。
3. 暗号・セキュリティ・ブロックチェーン
暗号技術の多くは、数論や代数構造といった抽象度の高い数学に支えられています。
- RSA暗号における素因数分解とオイラーの定理
- 楕円曲線暗号における群構造
- ハッシュ関数設計と確率的な衝突性の議論
実装者としてライブラリを使うだけなら高度な数論までは不要ですが、プロトコルの安全性を評価したり、新しい暗号方式を設計したりする立場では、数学の専門知識が不可欠です。
4. シミュレーション・物理エンジン・最適化
工学分野のシミュレーションや物流最適化、金融工学なども、数学をベースにした数値計算の世界です。
- 有限要素法(FEM)などの数値解析(偏微分方程式)
- 最短経路問題やスケジューリング(グラフ理論・組合せ最適化)
- ポートフォリオ最適化やリスク評価(確率微分方程式、確率統計)
これらの分野では、数学モデルをどのようにプログラムに落とし込むかが仕事そのものになるため、数学なしに成り立たないと言ってよい領域です。
「数学が必要」とされる理由は2つある
プログラミング学習において「数学が必要」と言われるとき、実は次の2つが混同されていることが多いです。
- コードを書くために、直接数学が必要になるケース
- 数学的な思考法(論理的・抽象的な考え方)が役に立つケース
1. コードそのものに数学が埋め込まれているケース
これは先ほど挙げたような、機械学習やCG、暗号などの分野です。
ここでは、数式とコードがほぼ1対1対応しており、数学を理解しているかどうかが、そのままプログラムの理解度につながります。
2. 思考法としての数学が活きるケース
一方で、多くのビジネス系開発やWebアプリ開発においては、数式自体よりも「考え方としての数学」が重要になります。
- 問題を小さな要素に分解し、前提を整理する
- 変数と条件を明確にし、矛盾がないかチェックする
- パターンを抽象化して、再利用しやすい形にまとめる
これは数学の証明問題や関数のグラフを考えるときのプロセスとよく似ています。
プログラミングは「論理の積み上げ」で動いているため、数学的な論理性になじみがある人ほど吸収が早い、という傾向は確かに存在します。
ただし、これは「数学ができないとプログラミングができない」という話ではありません。
プログラミングを学ぶ過程で、自然と論理的な考え方が鍛えられる側面も大きいからです。
プログラミングに役立つ「具体的な数学分野」
「どの程度の数学を押さえておけば安心なのか」を、レベル別に整理しておきます。
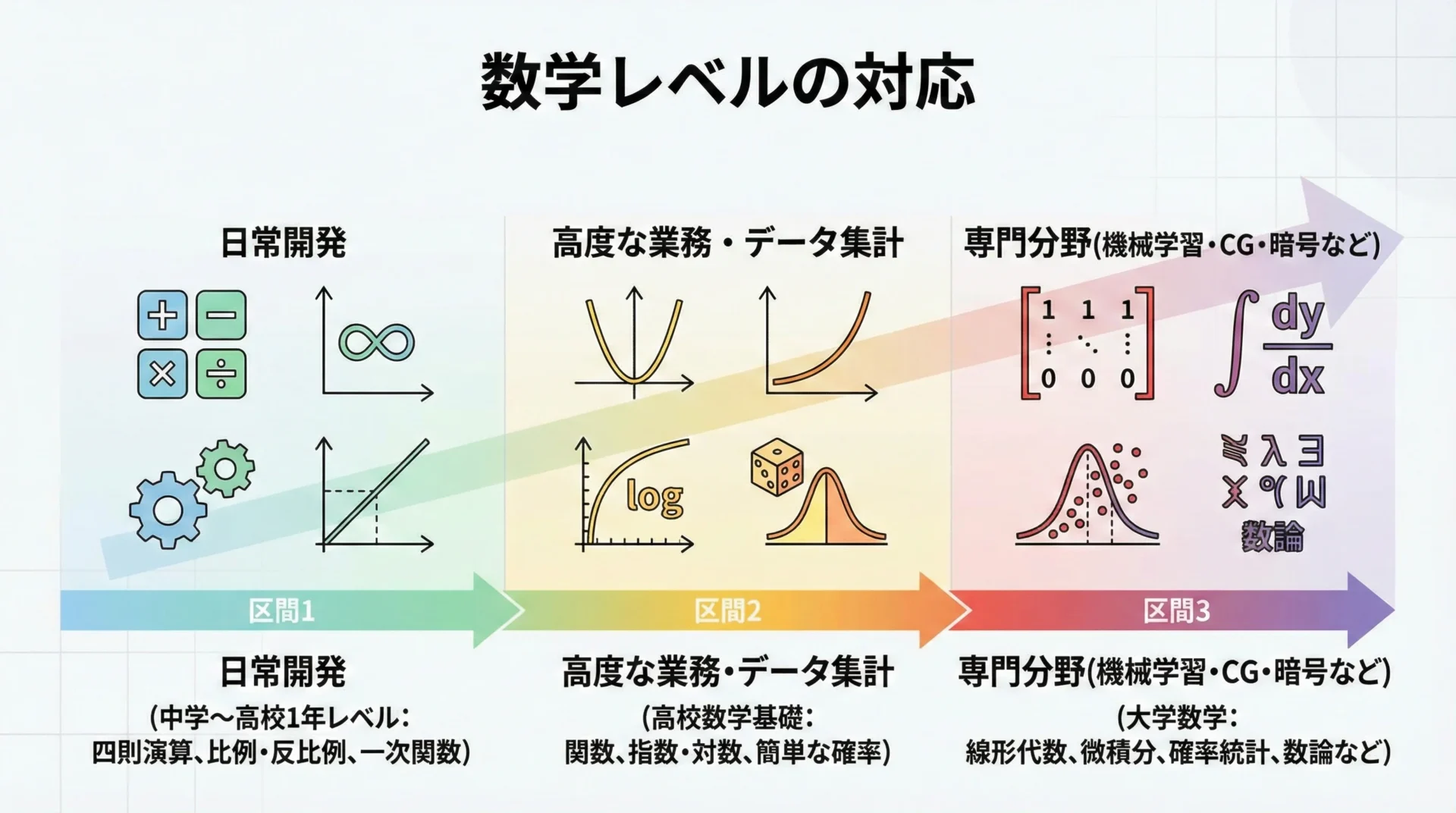
日常的な開発で特に役立つもの
日常的なWeb・業務開発で意識しておくと役立つのは、次のような範囲です。
- 四則演算と割合(売上や手数料の計算など)
- 一次関数レベルの関数概念(入力と出力の関係を意識する)
- 簡単な確率・統計(平均値や中央値、分散のイメージ)
これらは、中学〜高校初期レベルの内容に相当します。
学校の数学に苦手意識があっても、「実務でどう使うか」を意識して学び直すと、理解しやすくなることが多いです。
専門分野を目指す人が意識したいもの
機械学習やグラフィックスなど、数学が重要な分野を目指すなら、以下の分野は避けて通りにくいです。
- 線形代数(ベクトル・行列・固有値など)
- 微分積分(変化率や最適化の基礎)
- 確率・統計(確率分布、期待値、推定、検定)
- 分野によっては数値解析や離散数学(グラフ理論、論理学)
重要なのは、これらを「試験のために暗記する」のではなく、「コードで扱う対象として理解する」ことです。
例えば、行列演算をPythonで実装しながら学ぶと、式とプログラムが結びついて定着しやすくなります。
数学が苦手でもプログラマーになれるのか
多くの人が一番気にするのは、最終的にここだと思います。
答えは「なれます」。
ただし、目指す方向性によって、求められる数学の深さが変わります。
数学が苦手でも挑戦しやすい領域
次のような領域は、数学よりも設計力・コミュニケーション力・ドメイン知識の比重が高く、数学が大きなボトルネックになりにくいです。
- Webフロントエンド(画面設計、UI実装が中心)
- Webバックエンド(APIやDB設計、業務ロジック実装)
- スマホアプリのUI部分
- ノーコード / ローコードを活用した業務改善
もちろん、全く計算をしないわけではありませんが、中学レベルの算数をしっかり理解し直せば十分に戦える領域です。
数学が不安な人が意識したい学び方
数学が苦手だと感じる場合は、次のような進め方がおすすめです。
- 「学校数学の復習」ではなく、「プログラムで使うための数学」という視点を持つ
- 1つの公式を覚えるより、「どの場面で使うか」の具体例とセットで理解する
- 紙だけでなく、
Pythonなどのスクリプトで計算させながら学ぶ
こうすることで、数学そのものが目的ではなく、「作りたいものを実現するための道具」として自然に身についていきます。
まとめ
プログラミングにおける数学の必要性は、「どの分野で、どのレベルまでやりたいか」によって大きく変わります。
- 一般的なWeb開発や業務システム開発では、高度な数学はほとんど必要なく、中学〜高校初期レベルの算数・数学で十分なケースが大半です。
- 機械学習、コンピュータグラフィックス、暗号、シミュレーションなどの専門分野では、数学が仕事の中核にあり、線形代数・微積分・確率統計といった大学レベルの内容が求められます。
- 「数学が必要」という言葉には、式としての数学と思考法としての数学という2つの意味があり、後者は多くの開発領域でじわじわ効いてきます。
- 数学が苦手でも、プログラマーとして活躍できる領域は広く存在し、プログラミングを通じて論理的思考を鍛えながら、必要に応じて数学を「道具」として学び足していけば問題ありません。
自分が目指したいキャリアと興味のある分野を意識しながら、「今の自分にどの程度の数学が必要なのか」を逆算して学んでいくことが、遠回りをしないための近道になります。